
피드백 선형화를 이용한 쿼드로터의 자이로 효과 제어
© Korea Robotics Society. All rights reserved.
Abstract
This paper introduces a Feedback Linearization (FL) controller to eliminate the gyro effect on a quadrotor UAV. In order to control the attitude of the quadrotor, the second model equation was differentiated to the 4-th order to induce the control input to be revealed, and then a new control input was derived based on the attitude transformation equation with a gyro effect. For the initial quick posture control of the quadrotor, the existing yaw control was replaced with a separate controller. The simulation was conducted with an experiment in which FL control to remove the gyro effect was applied to the quadrotor and an experiment without removing the gyro effect, from the experimental results, the maximum error seen in each axial direction of the quadrotor was x = 0.22 m, y = 0.20 m, z = 0.16 m. Through the proposed method, the effect of the FL controller for controlling the gyro effect of the quadrotor was confirmed.
Keywords:
Quadrotor, Gyro Effect, Feedback Linearization1. 서 론
무인비행기(UAV : Unmanned Aerial Vehicles)는 원격 조정 되거나 스스로 조정되며 카메라, 센서, 통신장비 또는 장비를 탑재할 수 있는 비행체이다. 현재에는 기체의 형태에 따라 드 론(drone), 멀티콥터(multicopter) 등의 구체적인 명칭으로 불 리고 있으며, 군사용에는 고속 주행이 가능하면서 미사일의 탑재가 가능한 드론이 주로 쓰이고 있고, 도심지 촬영이나 가 벼운 물류배송, 게임과 레저 등에서는 속도는 느리지만 움직 임이 보다 자유로운 멀티콥터가 보다 유리하다. 이 중에서도 많은 로터 개수를 가지는 비행체를 멀티콥터라 부르는데 비행 에 필요한 최소한의 4-로터(rotor)만으로 비행이 가능한 비행 체를 쿼드로터(quadrotor)라 부르고 있다.
UAV 시스템 연구는 비행체의 자세제어에 대한 연구가 주 를 이루고 있다. 특히, 쿼드로터는 일반적으로 호버링 성능이 우수하고 기계적 구조가 간단하여 제작 및 유지보수 비용이 적게 들며, 로터의 운동에너지가 4개의 추력기로 분산되어 기 동력 및 적재능력이 우수하여[1,2], 근래에 많은 분야에서 이러 한 쿼드로터를 이용하려는 연구가 진행되고 있다[3-5]. 이 과정 에서 쿼드로터 내부 동특성에 영향을 미치는 모델 파라미터의 불확실성과 공기역학에 영향을 받는 비선형 모델 제어 기술[6], 적정한 추력 값을 분산시켜야 하는 조건을 만족하면서 모터 추력상수와 항력계수의 변동 등에도 강인한 제어 기술[7], 배터 리 기반 구동에 따른 짧은 운용시간을 극복하기 위한 기술[8], 지면효과가 기체의 착륙에 미치는 영향 등을 분석한 연구들이 있었지만[9,10], 자이로 효과(gyro effect)가 쿼드로터에 미치는 영향에 대한 연구는 미미하다.
자이로 현상은 회전체가 중심축을 기준으로 고속으로 회전 할수록 축 자세를 유지하려는 팽이의 세차운동을 생각해보면 쉽게 이해할 수 있다. 회전익 4개를 구동기로 사용하는 쿼드로 터에서도 자이로 현상이 존재하는데 [11], [12]의 연구에서는 구동기의 대칭적인 배치와 서로 반대방향으로 회전하는 기체 의 특이성으로 인해 yawing 모멘트에서 발생하는 프로펠러 자 이로 효과는 존재하지 않으나 쿼드로터 기체에는 자이로 효과 가 존재하며 rolling, pitching 모멘트에서는 프로펠러 자이로 효과가 존재함을 수식으로 정리하여 보였다. 단, 쿼드로터 운 동 과정에서 발생하는 작은 변수항 토크 정도로 여겨 목적에 따라 생략하거나 공기역학적 요소와 블레이드의 조건에 대한 고려가 복잡해지기 때문에 다루지 않는 경우가 많다. 해외의 여러 논문에서 자이로 효과에 대하여 수학적으로 명시하고 있 기 때문에 쿼드로터의 비행에서 자이로 효과가 얼마나 영향을 미치는지에 대하여는 다루어 볼 필요가 있다.
먼저, 쿼드로터의 모델 방정식을 정의하는 기준은 여러 논 문에서 제시되었다[13,14]. 대표적으로 많이 쓰이는 모델 방정식 은 쿼드로터의 수직력을 좌표변환을 통해 3방향의 위치운동 으로 나타내는 위치 운동방정식과 roll, pitch, yaw 오일러 각을 정의하는 회전 운동방정식으로 이루어져 있다. 회전 운동에 대한 방정식은 연구마다 차이를 보이는데 고려해야 할 여러 요소로써 추력, 관성모멘트, 각속도 등을 들 수 있다[15]. 다양한 목적에 따라 각 연구에서는 이 과정에서의 회전 운동방정식이 간소화 되거나 생략되어 자세제어가 이루어지고 있다[16-19]. 본 연구에서는 공기역학적인 요소나 프로펠러에 대한 고려는 제 외하고, 회전 운동의 각속도와 관성 모멘트만으로 간략하게 반영되어진 [15]의 위치와 회전 운동방정식을 사용하여 자이 로 효과가 쿼드로터에 미치는 영향을 확인하였다.
쿼드로터 제어방법으로는 비선형 모델에 대하여 수학적 모델 링을 기반으로 한 피드백 선형화 방법(FL : Feedback Linearization) 의 적용에 대한 연구가 특히 많이 이루어지고 있다[20-24]. 본 연구 에서는 [19]의 연구에서 제시한 동적 확장을 통한 FL제어입력 유 도 방법을 기반으로 쿼드로터의 자이로 효과를 상쇄하기 위한 새 로운 제어입력을 제시하며, 주요 내용 및 구성은 다음과 같다.
2장에서 자이로 효과를 가지는 쿼드로터 모델에 대해 기술 하고, 3장에서는 FL에 기반한 제어입력의 유도 방법을 제시한 다. 4장은 시뮬레이션을 통해, 제시된 방법에 의해 자이로 효 과가 쿼드로터의 운동에 미치는 영향을 보이고, 마지막으로 5 장에서 결론을 맺는다.
2. 시스템 모델링
쿼드로터 시스템은 [Fig. 1]에 도시된 바와 같이 4개의 로터 에 의해 구동되며, 각 로터의 회전 속도에 의해 자세 및 위치 제 어를 수행한다. 본 연구에 사용된 로터는 x축과 y축에 대해 대 칭이고, 무게중심과 기하중심과의 거리는 0이며, 무게중심으 로부터 막대의 끝에 위치한 각 로터까지의 거리는 l (m)이다. 각 로터는 x-y 평면에 대하여 직각방향으로 추력 Fi (i = 1, 2, 3, 4)을 발생시킨다. Jx, Jy, Jz는 각 축에 대한 관성 모멘트 (Nms2/rad) 이며, m은 질량(kg)이다. 여기서, 식 (1)의 u1은 쿼 드로터의 수직력 제어, u2, u3, u4는 각각 roll (ϕ), pitch (θ), yaw (ψ) 제어입력이며, 로 두어 그 유도된 위치 운동방정식과 회전 운동방정식은 식 (1)~(4)와 같다.
| (1) |
| (2) |
| (3) |
| (4) |
여기서, [ϕ, θ, ψ]T는 오일러 각, 은 기체의 각속도, g 는 중력가속도를 나타내며, sin(*), cos(*), tan(*), sec(*)는 s(*), c(*), t(*), sc(*)로 표기하였다.
3. 제어기 설계
먼저 FL방법을 적용하기 위해 쿼드로터의 출력을 x, y, z와 ψ의 4개로 두고, 식 (2)의 우변에 제어입력 u2, u3, u4가 명시적 으로 나타날 때까지 연속 미분을 취하는 동적 확장(dynamic extension)을 수행한다[19].
[19]의 연구와 달리 본 연구에서는 자이로 현상이 반영되도 록 식 (3)~(4)로 정의하였기 때문에 동적 확장으로부터 얻어낸 가상의 제어입력은 와 같다. 유도과정은 Appendix 의 (A1)-(A6)에 보이며, 이를 식 (A7)로 정리하면 쿼드로터의 최종 출력방정식은 아래의 식 (5)와 같이 정의된다.
| (5) |
여기서, 이며, 오일러 각 를 대체하기 위한 실질적인 제어입력 u2, u3, u4은 식 (3)를 미분하여 식 (6)의 형태로 변환하여 얻어 질 수 있다.
| (6) |
여기서, 이고, 식 (6)을 정리하면 제 어입력은 아래의 식 (7)과 같다.
| (7) |
이제, 식 (7)의 가상 제어입력을 최종 출력방정식 식 (5)에 대입하여 정리하면 쿼드로터에서 발생되는 자이로 효과 가 반영되는 최종 제어입력 이 식 (8), (9)와 같이 정리된다.
| (8) |
| (9) |
여기서, uα1은 uα의 첫째 행, uR2는 uR의 둘째 행, uR3은 uR 의 셋째 행, uR4는 uR의 넷째 행이다. 동적 확장의 결과, 이제 식 (5)로부터 자이로 효과를 상쇄하기 위한 FL에 기반한 제어 입력은 식 (10)과 같다.
| (10) |
여기서,
| (11) |
| (12) |
여기서, U는 쿼드로터에 발생되는 자이로 토크를 상쇄하기 위한 최종 제어입력이며, U0는 자이로 효과가 포함된 쿼드로 터의 피드백 선형화를 위하여 동적 확장을 통하여 유도된 제 어입력이며, 는 Error dynamics를 계산하기 위한 가상 입력으로 이고 xd, yd, zd는 각각 해당하는 기준입력, kij>0 (i = 1, 2, 3, j = 1, 2, 3, 4)이다. 그리고 [19]의 연구를 참고하여 급속한 초기 안정성을 위해 yaw 제어는 식 (11)의 u4를 식 (13)으로 대체하였다.
| (13) |
식 (10)의 우변에서 FG, TR 은 식 (8)에서 나타나는 쿼드로 터의 자이로 효과를 상쇄하기 위한 제어입력으로 식 (14)와 같 으며, 두 항으로 분리되어 입력이 구성된 이유는 동적 확장을 통하여 새로운 피드백 선형화 입력 을 유 도하기 위하여 식 (3)을 미분하는 과정에서 기체의 각가속도 를 나타내는 식 (4)의 항이 두 가지 요소의 합으로 이루어져 있 기 때문이다.
| (14) |
4. 실험 및 결과
본 논문에서는 제안된 FL방법을 이용하여 쿼드로터를 제 어하는 시뮬레이션을 진행하였고 그 결과를 보인다. 먼저, 시 뮬레이션에 적용된 모델 파라미터 상수는 아래와 같다.
- l = 1 m,
- g = 9.81 m/s2,
- Jx = Jy = 0.02 Nms2/rad, Jz = 0.03 Nms2/rad.
쿼드로터의 초기 오일러 각은 ϕ0 = 20°, θ0 = 10°, ψ0 = 0°으 로 정하고, 비행 중 자이로 효과의 영향이 잘 드러나도록 나선 형 궤적을 따라 비행하도록 하였으며, 시뮬레이션은 30초(sec) 동안 진행하였다.
쿼드로터 시작지점(x0, y0, z0)은 (10, 0, 0)이며, 목표 도 착지점(xf, yf, zf)은 (10, 0, 20)이다. FL제어기의 게인 는 LQR (Linear Quadratic Regulator) 방법으로 계산된 값을 적용하였다[19].
[Fig. 2]는 지상에서 이륙한 쿼드로터가 나선형 궤적을 보이 며 목표고도에 도달하는 FL제어 결과를 나타낸다. [Fig. 3(a)]는 자이로 효과를 상쇄하기 위한 Fg, Tr항이 FL제어기에 포함 된 쿼드로터의 비행 궤적과 포함되지 않은 비행궤적 두 가지 를 z축 (+)방향에서 비교하여 보인다. 여기서 각 FL제어에 따 른 비행 궤적은 목표를 따라 잘 추종하고 있는 것으로 보이지 만 [Fig. 3(b)]에서 각 축 방향에서 발생하는 위치 오차를 확인 할 수 있다. 각 축 방향에서의 최대 오차는 x = 0.22 m, y = 0.20 m, z = 0.16 m 만큼 발생함을 보였다.
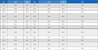
자이로 효과를 상쇄하기 위한 쿼드로터 FL제어 입력의 Fg, Tr항에서 측정된 결과는 [Fig. 4(a)], [Fig. 4(b)]에 보이며, 그 값은 아래와 같다.
[Fig. 5]는 자이로 효과를 상쇄하는 FL제어기를 적용한 쿼 드로터의 자세제어 결과와 그에 따른 위치추종 결과를 나타낸 다. 시뮬레이션 결과 [Fig. 5(a)]에서처럼 쿼드로터는 50° 이내 에서 자세가 안정화됨을 보였다. 그리고 쿼드로터가 지상에서 출발하면 u1 초기 값에 따라 상승지연이 발생하는데 실험에 서는 u1 초기 값을 9.81 rad2/ms2으로 정하였다. 그 결과 2.2 초 후 상승을 시작하여 [Fig. 5(b)]와 같이 목표 궤적을 따라 비행 하는 것을 확인할 수 있다. 그리고 시뮬레이션이 진행되는 동 안 로터의 출력 는 [Fig. 5(c)]에서 보이듯 6 rad2/ms2 이내로 유지됨을 보였다. 자이로 효과를 상쇄하지 않 는 FL제어 결과에 비해 자세제어 결과에서 각각 최대 ϕ = 1.42°, θ = 2.17°, ψ = 1.36°의 차이를 보였다.
![[Fig. 5] [Fig. 5]](/xml/26075/JKROS-15-3-248_F5.jpg)
Position, attitude response, and control inputs in case of the gyro effect control of the quadrotor UAV using FL
본 연구에서 제시한 피드백 선형화를 이용한 쿼드로터의 자 이로 효과를 제어하는 방법이 외란으로부터 받는 영향을 확인 해보았다. 외란은 각각 에 대하여 사각파형 (Frequency : 1.0 Hz, Amplitude : 1.0, Offset : 1.0, %Duty cycle : 50.0)과 사인 파형 (Frequency : 1.0 Hz, Amplitude : 1.0, Offset : 1.0, Sample per period : 9)을, 에는 랜덤 노이즈 (Frequency : 10, Mean : 0.0, Standard deviation : 1.0)로 30 초 동안 인가되도록 하였다. 실험 결과 입력 외란의 0.1 배 이내에서 제어시스템이 무리없 이 동작하는 것을 확인하였고, 오차는 각각 최대 x = 0.30 m, y = 0.53 m, z = 0.04 m 의 차이를 보였다.
5. 결론 및 향후과제
본 논문에서는 피드백 선형화를 이용하여 쿼드로터의 자이 로 효과를 상쇄하는 제어기를 제시하였다. 쿼드로터의 FL제 어 입력을 유도하기 위하여 2차 위치 운동방정식을 4차까지 미분하여 가상의 제어입력 이 드러나도록 유도 한 후 여기서 다시 회전 운동으로 발생되는 자이로 효과를 반 영하는 새로운 제어 입력 으로 정리하였다. 시뮬레이션을 통하여 쿼드로터의 비행에서 나타나는 자이로 효과의 크기를 확인해 보았고, 제한된 환경 내에서 자이로 효 과를 상쇄하는 제어기를 적용한 결과 최대 0.22 m의 위치 오차 가 제거되는 것을 확인할 수 있었다.
본 연구에서는 쿼드로터에서 발생되는 자이로 효과와 이를 제어하기 위한 FL제어기를 제시하였으나, 피드백 선형화 제 어의 특성상 외란이나 불확실한 파라미터를 가지는 쿼드로터 에서 보이는 자이로 효과에 대한 연구는 더 필요할 것으로 보 이며 이는 향후 연구로 남겨둔다.
References
-
S. Gupte, P. I. T. Mohandas, and J. M. Conrad, “A Survey of Quadrotor Unmanned Aerial Vehicles,” 2012 IEEE Southeastcon, Orlando, USA, pp. 1-6, 2012,
[https://doi.org/10.1109/SECon.2012.6196930]

-
S. W. Jung, J. M. Koo, K. Y. Jung, H. J. Kim, and H. Myung, “Vision-based Autonomous Landing System of an Unmanned Aerial Vehicle on a Moving Vehicle,” Journal of Korea Robotics Society, vol. 11, no. 4, pp. 262-269, Dec., 2016,
[https://doi.org/10.7746/jkros.2016.11.4.262]

-
P. K. Freeman and R. S. Freeland, “Agricultural UAVs in the U.S.: potential, policy, and hype,” Remote Sensing Applications: Society and Environment, vol. 2, pp. 35-43, Dec., 2015,
[https://doi.org/10.1016/j.rsase.2015.10.002]

- K. B. Kim and B. G. Chung, “Technology Acceptance of Industry 4.0 Applying UTAUT2: Focusing on AR and Drone Services,” Journal of Information Technology Applications & Management, vol. 26, no. 6, pp. 29-46, 2019,
-
K. B. Kim and I. O. Jeon, “Influential Factors of Intention to Use Drone Technology: an Application of Extended UTAUT Model,” Journal of Distribution and Management Research, vol. 21, no. 3, pp. 161-173, 2018,
[https://doi.org/10.17961/jdmr.21.3.201806.161]

- A. Benallegue, A. Mokhtari, and L. Fridman, “Feedback Linearization and High Order Sliding Mode Observer For A Quadrotor UAV,” 2006 International Workshop on Variable Structure Systems, Alghero, Italy, pp. 365-372, 2006,
-
S. U. Din, Q. Khan, F. U. Rehman, and R. Akmeliawanti, “A Comparative Experimental Study of Robust Sliding Mode Control Strategies for Underactuated Systems,” IEEE/Access, vol. 5, pp. 10068-10080, 2017,
[https://doi.org/10.1109/ACCESS.2017.2712261]

-
H. C. Choi and N. H. Shin, “A Perching Mechanism of a Quadrotor for Energy Harvesting,” Journal of Korea Robotics Society, vol. 13, no. 3, pp. 198-204, 2018,
[https://doi.org/10.7746/jkros.2018.13.3.198]

-
Y. M. Kim and W. B. Baek, “Adaptive Sliding Mode Control based on Feedback Linearization for Quadrotor with Ground Effect,” Journal of Advanced Information Technology and Convergence, vol. 8, no. 2, pp. 101-110, 2018,
[https://doi.org/10.14801/JAITC.2018.8.2.101]

- I. C. Cheeseman and W. E. Bennett, “The Effect of the Ground on a Helicopter Rotor in Forward Flight,” Aeronautical Research Council Technical Report, No. 3021, 1955, [Online], http://naca.central.cranfield.ac.uk/reports/arc/rm/3021.pdf.
-
T. Hamel, R. Mahony, R. Lozano and J. Ostrowski, “Dynamic Modeling and Configuration Stabilization for an X4-flyer,” IFAC, Barcelona, Spain, vol. 35. no. 1, pp. 217-222, 2002,
[https://doi.org/10.3182/20020721-6-ES-1901.00848]

-
S. Bouabdallah and R. Siegwart, “Full Control of a Quadrotor,” 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, pp. 153-158, 2007,
[https://doi.org/10.1109/IROS.2007.4399042]

-
X. Zhang, X. Li, K. Wang, and Y. Lu, “A Survey of Modelling and Identification of Quadrotor Robot,” Journal of Abstract and Applied Analysis, pp. 1-13, 2014,
[https://doi.org/10.1155/2014/320526]

-
H. Shraim, A. Awada, and R. Youness, “A Survey on Quadrotr: Configurations, Modeling and Identification, Control, Collision Avoidance, Fault Diagnosis and Tolerant Control,” Journal of IEEE Aerospace and Electronic Systems Magazine, Vol. 33, No. 7, pp. 14-33, 2018,
[https://doi.org/10.1109/MAES.2018.160246]

-
I. H. Choi, M. H. Park, and H. G. Kim, “Non-linear Adaptive Attitude Controller Design of Quadrotor UAV,” IEEE Aerospace and Electronic Systems Magazine, vol. 13, no. 6, pp. 2421-2427, 2012,
[https://doi.org/10.5762/KAIS.2012.13.6.2421]

-
E. Zheng and J. Xiong, “Quad-rotor Unmanned Helicopter Control via Novel Robust Terminal Sliding Mode Controller and Under-actuated System Sliding Mode Controller,” Optik, vol. 125, no. 12, pp. 2817-2825, Jun., 2014,
[https://doi.org/10.1016/j.ijleo.2013.11.069]

-
H. Kim, H. S. Jeong, K. T. Chong, and D. J. Lee, “Dynamic Modeling and Control Techniques for Multi-Rotor Flying Robots,” Transactions of Korean Society of Mechanical Engineers-A, vol. 38, no. 2, pp. 137-148, 2014,
[https://doi.org/10.3795/KSME-A.2014.38.2.137]

-
M. Elsamanty, A. Khalifa, M. Fanni, A. Ramadan, and A. Abo- Ismail, “Methodology for Identifying Quadrotor Parameters, Attitude Estimation and Control,” 2013 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Wollongong, Australia, pp. 1343-1348, 2013,
[https://doi.org/10.1109/AIM.2013.6584281]

-
D. Lee, H. J. Kim, and S. Sastry, “Feedback Linearization vs. Adaptive Sliding Mode Control for a Quadrotor Helicopter,” Journal of Control, Automation, and Systems, vol. 7, no. 3, pp. 419-428, 2009,
[https://doi.org/10.1007/s12555-009-0311-8]

-
H. Voos, “Nonlinear Control of a Quadrotor Micro-UAV using Feedback- Linearization,” 2009 IEEE International Conference on Mechatronics, Malaga, Spain, pp. 1-6, 2009,
[https://doi.org/10.1109/ICMECH.2009.4957154]

-
D. H. S. Maithrripala and J. M. Berg, “Robust Tracking Control for Underactuated Autonomous Vehicles Using Feedback Linearization,” 2014 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Besason, France, pp. 446- 451, 2014,
[https://doi.org/10.1109/AIM.2014.6878118]

-
S. A. Al-Hiddabi, “Quadrotor Control using Feedback Linearization with Dynamic Extension,” 2009 6th International Symposium on Mechatronics and its Applications, Sharjah, United Arab Emirates, 2009,
[https://doi.org/10.1109/ISMA.2009.5164788]

-
D. E. Chang and Y. S. Eun, “Global Chartwise Feedback Linearization of the Quadcopter With a Thrust Positivity Preserving Dynamic Extension,” IEEE Transactions on Automatic Control, vol. 62, no. 9, pp. 4747-4752, 2017,
[https://doi.org/10.1109/TAC.2017.2683265]

-
D. Lee, H. Lee, J. Lee, and D. H. C. Shim, “Design, Implementation, and Flight Tests of a Feedback Linearization Controller for Multirotor UAVs,” International of Aeronautical & SpaceScience, vol. 18, no. 4, pp. 740-756, 2017,
[https://doi.org/10.5139/IJASS.2017.18.4.740]

2009 동의대학교 메카트로닉스공학과(학사)
2011 동의대학교 지능시스템공학과(석사)
2015~현재 동의대학교 지능시스템공학과 (박사수료)
관심분야: 쿼드로터 UAV, 비선형 시스템 제어, 슬라이딩 모드 제어

![[Fig. 1] [Fig. 1]](/xml/26075/JKROS-15-3-248_F1.jpg)
![[Fig. 2] [Fig. 2]](/xml/26075/JKROS-15-3-248_F2.jpg)
![[Fig. 3] [Fig. 3]](/xml/26075/JKROS-15-3-248_F3.jpg)
![[Fig. 4] [Fig. 4]](/xml/26075/JKROS-15-3-248_F4.jpg)


