CrabBot: 이중 4절 링크를 활용한 꽃게 모사 8족 주행 로봇
© Korea Robotics Society. All rights reserved.
Abstract
Milli-scale crawling robots have been widely studied due to their maneuverability in confined spaces. For successful crawling, the crawling robots basically required to fulfill alternating gait with elliptical foot trajectory. The alternating gait with elliptical foot trajectory normally generates both forward and upward motion. The upward motion makes the aerial phase and during the aerial phase, the forward motion enables the crawling robots to proceed. This simultaneous forward and upward motion finally results in fast crawling speed. In this paper, we propose a novel alternating mechanism to make a crab-inspired eight-legged crawling robot. The key design strategy is an alternating mechanism based on double four-bar linkages. Crab-like robots normally employs gear-chain drive to make the opposite phase between neighboring legs. To use the gear-chain drive to this milli-scale robot system, however, is not easy because of heavy weight and mechanism complexity. To solve the issue, the double-four bar linkages has been invented to generate the oaring motion for transmitting the equal motion in the opposite phase. Thanks to the proposed mechanism, the robot crawls just like the real crab with the crawling speed of 0.57 m/s.
Keywords:
Bio-inspired Robot, Hexapedal, Tripod1. 서 론
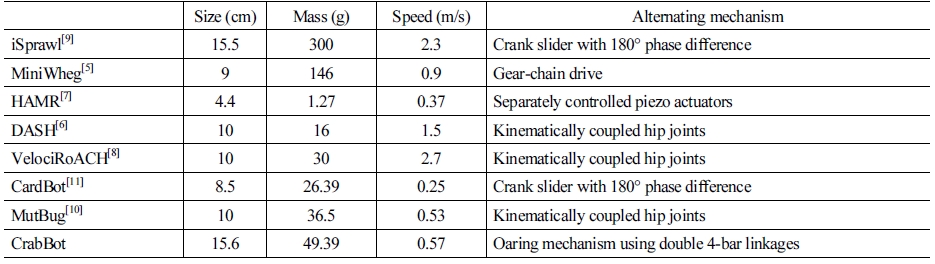
소형 다리형 로봇(crawling robot) 은 사람이 진입할 수 없는 동굴, 좁은 틈, 위험 지역 등을 정찰, 탐사할 수 있는 잠재력을 지니고 있다. 이렇듯 뛰어난 장점들을 가진 크롤링 로봇은 수 많은 로봇 연구자들에게 의하여 제작되었다[1-4]. MiniWhegs[5], DASH[6], HARM[7], VelociRoACH[8], iSprawl[9], MutBug[10], Cardbot[11] 등이 대표적인 소형 다리형 로봇이며, 크롤링 능력 에서 뛰어난 성능을 보여주었다.
언급된 로봇들은 세부적인 설계, 구조, 구동 방식, 성능에서 [Table 1]과 같이 차이가 존재한다. 그러나 기본적으로 다리의 교차적 움직임(alternating gait)이 성공적으로 구현되었다는 점에서 공통점을 가진다.
다리의 교차적 움직임은 소형의 다리형 로봇에서 중요한 의미를 가진다. 다리형 소형 로봇의 주행 속도를 높이기 위해 서는 로봇이 잠시라도 공중에 떠 있는 상태(aerial phase) 가 수 반되어야 한다. 공중에 띄우는 동시에 앞으로 밀어주는 모션 이 함께 나올 때, 소형 크롤링 로봇은 고속 주행을 위한 충분 조 건을 가지게 된다. 다리의 교차적 움직임은 aerial phase를 성 공적으로 만들어 내는 역할을 수행한다. 즉, 교차적 움직임이 제대로 수행되지 않으면, 로봇은 땅에 붙은 채로 저속의 주행 에 머무르게 된다.
성공적인 다리의 교차적 움직임을 만들기 위해, 다양한 형태의 메커니즘이 [Table 1]과 같이 사용되었다. iSprawl과 CardBot은 크랭크 슬라이드 메커니즘을 180° 위상차가 발생하 도록 하여 다리의 교차적 움직임을 구현하였다. Miniwheg는 기 어와 체인을 통해 각 다리의 일정한 위상차를 유지하였다. Smart composite microstructure (SCM) 생산방식 기반의 로봇들은 회전 조인트로 연결된 링크 설계를 통해 교차적 움직임을 만들었다. HAMR의 경우 각 다리당 2개씩의 piezo 구동기를 사용하여, 위 상차를 직접 제어하였다. DASH, VelociRoACH, MutBut는 hip joint가 지그재그 형태로 배치되도록 하였다. 위 로봇들은 다양 한 형태의 위상차 구현 메커니즘을 통해, 뛰어난 성능의 크롤링 로봇을 개발하였다. 또한, 로봇의 형태가 달라지면, 그에 따라 위상차 구현 메커니즘 역시 새로운 방식이 필요함을 알 수 있다.
본 논문에서는 새로운 형태의 위상차 구현 메커니즘에 기 반한 꽃게 모사 8족 크롤링 로봇 구현을 제안한다. 본 로봇은 좌우 두 쌍의 다리를 가지며, 각 다리는 두개의 발(point feet) 을 가진다. 두 쌍의 다리는 직렬(serial) 형태로 연결되어, 바깥 쪽의 다리에 반대 위상의 움직임을 전달하기 위한 메커니즘이 반드시 요구된다. 이를 해결하기 위해 4절 링크를 이중으로 사 용한 노 젓기 형태의 메커니즘을 고안하고 적용하였다. 이러 한 디자인 덕택으로, 기어 트레인을 단순화하는 동시에 구동 부를 몸체 가운데에 위치시킬 수 있었다.
이어질 섹션은 디자인, 모델링, 제작, 실험 및 결론 순으로 진행될 예정이다. 디자인 섹션에서는 로봇이 어떤 방식으로 구동되는지 소개할 것이다. 또한, 교차적 움직임(alternating gait)이 잘 일어날 수 있도록 기구의 운동학적(kinematic) 모델 링을 통해 발의 적절한 경로를 찾고 실험을 통해 실제 경로와 비교할 계획이다. 마지막으로 주행 테스트를 통해 교차적 움직 임(alternating gait)이 설계한 바와 같이 구현되는지 관찰한다.
2. 디자인
2.1 다리 디자인
본 로봇의 전체적인 디자인을 [Fig. 1]과 [Fig. 2] 나타내었다. 몸체 가운데에 구동부가 있으며, 구동부는 2개의 DC 모터를 가 지고 있다. 2개의 모터는 각각 왼쪽 다리와 오른쪽 다리의 구동 에 쓰인다. 구동부 양 옆으로는 2쌍의 다리가 위치하고 있다.
본 로봇의 다리 구동 메커니즘은 [Fig. 3]과 같이 Klann Linkage 의 모션을 이용하였다. Klann Linkage 모션은 회전 크랭크운 동을 타원형의 운동으로 바꿔준다. 이를 다리로 적용 시킬 경 우, 땅을 잡아 끄는 움직임을 보여준다. 이 같은 움직임을 이용 하여 Klann Linkage 두 개를 이어 붙여 한 쌍의 다리 구조를 완 성 시켰고, 이를 4개 배치하여 8족 로봇을 설계 하였다. 가운데 2쌍의 다리와 바깥쪽 2쌍의 다리가 서로 교차하며 움직이면서 앞으로 진행한다. 이때, 양 쪽의 DC모터의 속도를 제어하여 방향전환도 가능하다.
2.2 동력전달 디자인
2쌍의 다리당 하나의 DC모터로 구동된다. 이때 중요한 것 은 안쪽 다리와 바깥쪽 다리의 위상 차이가 180°로 항상 유지 되어야 성공적인 크롤링 모션 구현이 가능하게 된다. [Fig. 4], [Fig. 5]와 같이 이중 4절 링크에 기반한 노 젓기 메커니즘이 이 역할을 수행한다. 모터가 회전하면서 안쪽 다리에 동력을 전 달하고, 이중 4절링크를 거쳐 바깥쪽 다리로 반대 위상의 동력 이 전달된다. [Fig. 4]에 동작 방식이 묘사되어 있다. 시계방향 으로 모터가 회전하면 모터와 같은 위상에 있는 링크는 같은 방향으로 회전하고, 반대 방향에 연결된 링크는 모터와 역방 향의 위상(Reverse phase)을 가지게 된다. 이는 [Fig. 5]에도 나 와 있듯이, 고정된 링크(Fixed axis)와 이중 4절 링크(Double 4-bar)의 가운데 링크가 조인트로 연결되면서 2차원 움직임만 가능한 4절링크가 3차원 움직임으로 변화하며 가능한 메커니 즘이다. 때문에 모터와 연결된 링크와 반대 위상의 링크에 다 리 구조를 설치하면 교차로 기어가는(alternating gait)움직임 을 구현해낼 수 있다. 또한, 이러한 메커니즘을 응용하여 2개 의 이중4절 링크를 직렬로 추가한다면 1개의 모터로 수십 개 의 다리 주행 로봇을 설계할 수 있다.
2.3 제작
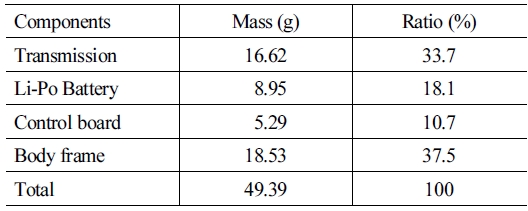
본 로봇은 [Fig. 6]과 같이 SCM (smart composite microstructure) 방식으로 제작되었다. 레이저 머시닝을 통해 도면이 옮겨진 종이 를 천을 사이에 두고 접착제로 부착한다. 이 같은 과정으로 천보다 상대적으로 강도가 높은 종이가 링크가 되며 천은 조인트 역할을 하게 된다. 나아가, SCM 공법은 나사와 같은 부품을 최소화 할 수 있어, 복잡한 링크를 편리하고 빠르게 구현 해볼 수 있다는 장점이 있다. 로봇 전체의 mass budget은 [Table 2]와 같다.
3. 다리 경로 분석
크롤링 로봇의 주행 속도를 결정하는 것은 발 경로(Foot path)의 모양이다. 경로가 원형보다는 납작한 타 원형에 가까 울수록 로봇은 진동을 최소화 하고 부드럽게 주행 가능하다. 납작한 타원형의 궤적은 왕복 운동시 발생하는 발 끝 궤적의 높낮이 차이를 줄여 주게 되어, 상하의 진동을 감소시키는 동 시에 안정적인 주행을 가능케 한다. 또한, 로봇의 속력 역시 최 대화 된다. 궤적이 납작한 타원에 가깝게 되면, 한 번에 치고 나갈 수 있는 보폭(Stride length)이 길어 지게 된다. 따라서, 같 은 속도의 모터를 사용할 경우, 주행 성능을 증대시킬 수 있다. 궤적 경로를 파악하기 위해, 발의 경로를 [Fig. 7]을 토대로 다 음과 같이 다리 끝의 위치 해석을 수행하였다.
| (1) |
| (2) |
| (3) |
| (4) |
식 (1)~(4)를 연립하여 모터 인풋 θ1에 대한 θ2, θ3, θ4, θ5 값 을 구한다. 구한 변수를 토대로 식 (5), (6)에 대입한다. 그리고 발 끝의 위치를 MATLAB의 fsolve 함수를 활용하여 분석한다.
| (5) |
| (6) |
4. 실험 및 결과
4.1 발 궤적 분석
앞서 말했듯이, 발의 궤적이 납작한 타원형에 가까울수록 빠르고 안정적인 주행을 할 수 있다. [Fig. 8]은 이론 식을 통해 구한 발의 궤적과 실제 다리 궤적의 비디오 분석을 통한 결과 를 나타낸 것이다. [Fig. 8]을 통해 이론 값과 실제 제작된 로봇 의 발 궤적 차이를 알 수 있다.
![[Fig. 8] [Fig. 8]](/xml/26096/JKROS-14-4-245_F8.jpg)
Foot trajectory of the front foot. The modeling data (left) and the experimental data (right). The shaded circles are when the leg goes outward in the air and the non-shaded circles are when the leg comes back.
전체적인 모양의 경우, 이론 값과 실제 궤적 모두 납작한 타 원형에 가까운 궤적을 보이고 있다. 그러나 세부적인 값에서 는 수 mm의 차이를 보인다. [Fig. 8(a)]의 이론 값은 발이 왕복 시에 1 mm 정도의 상하 차이가 발생하는 것을 볼 수 있다. 그 러나 실제 측정치의 경우에는 약 4 mm 정도의 상하 차이가 존 재한다. 이러한 오차는 제작 과정에서 발생하는 것으로 생각 된다. 설계 도면과 실제 제작 시에, 조인트 너비와 링크의 길이 는 레이저 커팅 머신의 정밀도에 따라 많게는 0.3 mm 정도의 오차가 발생할 수 있다. 이러한 길이 오차가 누적되면, 발의 궤 적에 영향을 끼칠 수 있다. 그러나, 전체적인 궤적의 모양을 보 았을 때, 의도한 바와 같이 납작한 타원형의 형태를 가지도록 설계된 것을 확인할 수 있다.
4.2 주행 테스트
이러한 주행 안전성을 직접 실험하기 위해, [Fig. 9]와 같이 고속 카메라 촬영을 통해 로봇의 질량 중심을 기준으로 주행 시 높이 변화를 관찰하였다. 이때, Kinovea 프로그램을 사용하여 데이터를 추출하여 그래프로 나타내었다. 그래프는 [Fig. 10(a)] 와 같다. 이때, 그래프를 분석해 보면, 최고점과 최저점을 극단 치(outlier)로 제외하였을 때 질량 중심의 높이 변화가 15 mm 내외를 유지하면서 주행하며, 이는 로봇 높이 86 mm의 17.4% 에 해당한다. 또한, [Fig. 10(b)]의 그래프를 보면 로봇의 수평 적 움직임을 관찰 할 수 있다. 즉, 시간당 거리 변화를 알 수 있 다. 이러한 데이터를 이용하여, 로봇의 평균속도가 0.57 m/s (3.65 body length/s) 라는 것을 판단 할 수 있다.
4.3 다리 궤적 모양에 관한 고찰
본 논문에서는 로봇이 원형 보다는 타원형에 가깝도록 의 도하여 설계하였다. 그 이유는 궤적의 높낮이 차이를 감소시 켜 로봇의 주행 안정성을 높이기 위함이다. 실제로 궤적의 높 낮이가 클 경우에는, 상하 진동이 함께 증가하여 로봇이 통통 튀는 모습을 보인다. 이를 방지하기 위해 궤적을 매우 납작한 타원형으로 구성할 경우에는 반대로 로봇의 주행 속도가 늦어 지게 된다. 로봇을 공중으로 띄워 마찰을 줄인 상태에서 밀어 주어야 하는데, 너무 납작한 경우에는 공중으로 띄워주는 것 이 어렵게 된다. 이에 대해서 경험적으로 학습하였기 때문에, 추가적인 정량적 분석이 필요할 것으로 판단된다.
5. 결 론
소형 크롤링 로봇은 각자의 로봇 형태에 맞는 고유한다리 위상차 구현 메커니즘을 보유하고 있다. 본 논문에서는 꽃게 모사 소형 8족 크롤링 로봇을 위한 이중 4절 링크 기반의 노 젓 기 메커니즘을 고안하고 적용하였다. 제안한 이중 4절 링크 기 반의 위상차 구현 메커니즘은 하나의 구동기를 사용하여, 이론적으로는 직렬로 무한개의 다리를 연결하여 구동할 수 있 다. 이중 4절 링크를 사용하여 불필요한 트랜스미션의 구성 요 소를 삭제할 수 있었고, 구동부을 로봇의 중심으로 위치시켜 주행 안정성을 확보하였다.
이러한 연구로 본 논문은 새로운 동력전달 구조를 소개하 고 효율성을 검증하였다. 나아가, 개발한 이중 4절링크를 응용 할 수 있는 새로운 로봇에 대한 연구가 가능할 것으로 생각된다.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korean Government (MSIP) (NRF-2016R1A5A1938472).
References
-
D.-S. Kim, S.-P. Jung, and G.-P. Jung, “A Milli-Scale Hexapedal Robot using Planar Linkages,” Journal of Korea Robotics Society, vol. 13, no. 2, pp. 97-102, Jun., 2018.
[https://doi.org/10.7746/jkros.2018.13.2.097]

-
G.-P. Jung, C. S. Casarez, S.-P. Jung, R. S. Fearing, and K.-J. Cho, “An Integrated Jumping-Crawling Robot using Height- Adjustable Jumping Module,” 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, pp. 4680-4685, 2016.
[https://doi.org/10.1109/ICRA.2016.7487668]

-
Y.-S. Kim, G.-P. Jung, H. Kim, K.-J. Cho, and C.-N. Chu, “Wheel Transformer: A Wheel-Leg Hybrid Robot With Passive Transformable Wheels,” IEEE Transactions on Robotics, vol. 30, no. 6, pp. 1487-1498, Dec., 2014.
[https://doi.org/10.1109/TRO.2014.2365651]

-
S. D. de Rivaz, B. Goldberg, N. Doshi, K. Jayaram, J. Zhou, and R. J. Wood, “Inverted and vertical climbing of a quadrupedal microrobot using electroadhesion,” Science Robotics, vol. 3, no. 25, p. eaau3038, 2018.
[https://doi.org/10.1126/scirobotics.aau3038]

- J. M. Morrey, B. Lambrecht, A. D. Horchler, R. E. Ritzmann, and R. D. Quinn, “Highly mobile and robust small quadruped robots,” 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, pp. 82-87, 2003
-
P. Birkmeyer, K. Peterson, and R. S. Fearing, “DASH: A dynamic 16g hexapedal robot,” 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO, USA, pp. 2683-2689, 2009
[https://doi.org/10.1109/IROS.2009.5354561]

-
A. T. Baisch, C. Heimlich, M. Karpelson, and R. J. Wood, “HAMR3: An autonomous 1.7g ambulatory robot,” 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, Francisco, CA, USA, pp. 5073-5079.
[https://doi.org/10.1109/IROS.2011.6095063]

-
D. W. Haldane and R. S. Fearing, “Running beyond the bio-inspired regime,” 2015 IEEE International Conference on Robotics and Automation, Seattle, WA, USA, pp. 4539-4546, 2015.
[https://doi.org/10.1109/ICRA.2015.7139828]

-
S. Kim, J. E. Clark, and M. R. Cutkosky, “iSprawl: Design and Tuning for High-speed Autonomous Open-loop Running,” (in en), The International Journal of Robotics Research, vol. 25, pp. 903-912, Sept., 2006.
[https://doi.org/10.1177/0278364906069150]

-
T.-Y. Kim, C. Kim, S.-H. Kim, and G.-P. Jung, “MutBug: A Lightweight and Compact Crawling Robot That Can Run on Both Sides,” IEEE Robotics and Automation Letters, vol. 4, no. 2, pp. 1409-1415, Apr., 2019.
[https://doi.org/10.1109/LRA.2019.2895896]

-
J.-E. Lee, G.-P. Jung, and K.-J. Cho, “Bio-inspired design of a double-sided crawling robot,” Conference on Biomimetic and Biohybrid Systems, pp. 562-566, 2017.
[https://doi.org/10.1007/978-3-319-63537-8_50]


![[Table 1]](../img/npr_tablethum.jpg)
![[Fig. 1] [Fig. 1]](/xml/26096/JKROS-14-4-245_F1.jpg)
![[Fig. 2] [Fig. 2]](/xml/26096/JKROS-14-4-245_F2.jpg)
![[Fig. 3] [Fig. 3]](/xml/26096/JKROS-14-4-245_F3.jpg)
![[Fig. 4] [Fig. 4]](/xml/26096/JKROS-14-4-245_F4.jpg)
![[Fig. 5] [Fig. 5]](/xml/26096/JKROS-14-4-245_F5.jpg)
![[Fig. 6] [Fig. 6]](/xml/26096/JKROS-14-4-245_F6.jpg)
![[Fig. 7] [Fig. 7]](/xml/26096/JKROS-14-4-245_F7.jpg)
![[Fig. 9] [Fig. 9]](/xml/26096/JKROS-14-4-245_F9.jpg)
![[Fig. 10] [Fig. 10]](/xml/26096/JKROS-14-4-245_F10.jpg)