평면기구 메커니즘을 이용한 소형 6족 로봇
© Korea Robotics Society. All rights reserved.
Abstract
A small and lightweight crawling robots have been actively studied thanks to their outstanding mobility and maneuverability. Those robots can navigate into more confined spaces that larger robots are unable to reach or enter such as debris and caves. In this paper, we propose a milli-scale hexapedal robot based on planar linkage design. To make this possible, two necessary conditions for successful crawling are satisfied: thrust force from the ground and aerial phase while running. These conditions are achieved through a newly developed leg design. The robot has a pair of legs and each leg has three feet. Those feet alternatively moves based on 1DOF planar linkage. This linkage is installed at each side of the robot and finally the robot shows the alternating gait and aerial phase during running. As a result, the robot runs with the crawling speed of 0.9 m/s.
Keywords:
Bio-inspired Robot, Hexapedal, Tripod1. 서 론
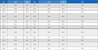
소형의 경량 크롤링(crawling) 로봇은 작고 가벼워 좁은 틈 과 같이 제한된 공간에 쉽게 접근할 수 있다는 장점을 가진다. 또한, 바퀴가 아닌 다리(legged crawling) 를 통해 보다 높은 장 애물을 극복 가능하다. 이러한 장점으로 연구자들은 다양한 형태의 구동 메커니즘을 가지는 소형 크롤링 로봇들을 [Table 1]과 같이 개발 하였다.
[Table 1], [Fig. 2]와 같이 로봇들은 제각기 다른 구동 방식 을 통해 설계되었다. 그러나 해당 소형 크롤링 로봇들은 성공 적인 주행을 위해 갖추어야 할 필수 조건을 공통적으로 가지 고 있다. 원활한 크롤링을 위해서는 다리들의 움직임 사이에 모든 다리가 공중에 떠 있는 시간(aerial phase) 과 로봇을 앞으 로 밀어주는 추진력이 필수적이다[1]. 연구자들은 이를 충족시 키기 위해 다양한 방식의 기구적 설계를 제안하였다.Table 2
RoACH[2] 는 smart composite microstructure (SCM)[3] 방식 으로 개발된 최초의 크롤링 로봇으로 2.4 g의 가벼운 질량, 3 cm의 작은 크기를 가진다. 또한, 형상 기억 합금(shape memory alloy) 구동기를 사용하여 노를 젓는 듯한 움직임 구현을 통해 0.03 m/s의 크롤링 속력을 달성하였다.
DASH[4] 는 하나의 DC 모터를 사용하여 1.5 m/s의 크롤링 속력을 달성하였다. RoACH와 동일하게 노 젓는 모션을 4절 링크와 모터-크랭크를 통해 구현하였다. VelociRoACH[5], [6] 는 DASH의 크롤링 속력을 극대화한 버전으로 2.7 m/s 의 속력 을 가진다. 모터-크랭크와 최적화된 4절 링크 디자인을 통해 고속의 노 젓기 모션을 달성하였다.
HAMR-VP[7-9] 는 동전 크기의 초소형 로봇으로 0.44 m/s의 속력으로 크롤링 가능하다. HAMR-VP 역시 노 젓는 모션을 구현하고자 하였다. Spherical 5 bar를 통해 힙 조인트(hip joint) 를 설계하였으며, 두 개의 압전 소자를 사용하여 다리를 구동 하였다.
CardBot[10] 은 양면 주행이 가능한 크롤링 로봇으로 8.5 cm 의 크기와 0.25 m/s의 주행 속력을 가진다. CardBot은 앞선 로 봇들과는 달리 평면 밖(out-of-plane) 모션이 아닌 평면 메커니 즘(planar mechanism) 을 통해 주행을 구현하였다. 평면 메커 니즘 구현을 위해 한 방향으로만 접히는 비등방성(anisotropic) 다리를 핵심 요소로 설계하였다.
Fig. 1과 같이 고속주행이 가능한 소형 6족 크롤링 로봇을 제안한다. 본 로봇은 좌우 한 쌍의 다리를 가지며 각 다리는 3 개의 발(point feet) 을 가진다. 3개의 발은 1자유도의 평면 기구 (planar linkage)로 구성되며, 하나의 DC 모터로 교차적 움직임 을 구현할 수 있다. 이를 통해, 로봇이 가지는 한 쌍의 다리는 삼각의 교차적 움직임(tripod alternating gait) 을 생성하여 성 공적인 크롤링 모션을 보여준다.
이어질 섹션은 디자인, 모델링, 제작, 실험 및 결론 순으로 진행될 예정이다. 디자인 섹션에서는 1자유도 다리 디자인과 어떤 방식으로 구동되는지 소개할 것이다. 또한, 교차적 움직 임(alternating gait)이 잘 일어날 수 있도록 기구의 운동학적 (kinematic) 모델링을 통해 발의 적절한 경로를 찾고 실험을 통 해 실제 경로와 비교할 계획이다. 마지막으로 주행 테스트를 통해 교차적 움직임(alternating gait)과 공중에 뜨는 위상(aerial phase)이 잘 나타나는지 확인할 것이다.
2. 로봇 디자인
2.1 다리의 교차적 움직임
성공적인 크롤링 모션을 구현하기 위해서는 로봇의 모든 다리가 공중에 뜨는 위상(aerial phase) 을 가져야한다. 본 로봇 은 다리의 교차적 움직임(alternating gait) 을 통해 걸음걸이 (gait) 중간에 공중에 뜨는 위상(aerial phase)이 발생할 수 있도 록 설계되었다. 로봇의 다리는 3개의 발(point feet)로 이루어 진 한 쌍의 다리(leg)를 가지며, 좌, 우에 하나씩 가지고 있다. 3 개의 발을 하나의 다리로 연결하기 위해서, 또 한 개의 모터로 3개의 발을 동시에 구동하기 위해서 본 로봇의 다리는 3개의 4 절 링크(four-bar linkage)로 구성되었다.
[Fig. 3]는 한 쪽 다리의 움직임을 연속 그림으로 보여준다. [Fig. 3 (a)]의 가장 오른쪽에 위치한 4절 링크에서, 파란색 점 과 연결된 노란색 링크는 동력원과 연결되어 크랭크 역할을 수행하며 다리에 동력을 전달한다. 오른쪽 4절 링크와 가운데 에 위치한 4절 링크는 하나의 크랭크를 공유하면서 동시에 움 직이게 된다. 그러나 이 때, 두 4절 링크는 180°의 위상 차이를 유지하며 구동한다. 따라서, 각 링크 끝에 위치한 다리 역시 반 대의 위상을 가지며, 한 다리가 땅에 닿으면 다른 다리는 공중 에 위치하게 되어 교차적 움직임을 생성한다. 또한, 가운데에 위치한 4절 링크의 한 변이 가장 왼쪽의 4절 링크 구동을 위한 크랭크 역할을 수행한다. 이로 인해, 왼쪽에 위치한 4절 링크 도 동시에 움직이게 된다. 뿐만 아니라, 오른쪽 4절 링크와 동 일한 움직임을 구현하고자 대칭 형태로 링크를 설계하였으며, 발의 위상 역시 오른쪽 4절 링크와 일치한다.
[Fig. 3]에 보이는 것처럼 각 4절 링크가 회전이 가능하도록 다리의 세 조인트를 몸체에 고정하고, 다른 조인트 하나는 회 전하는 동력원에 연결하여 이를 통해 다리에 동력이 전달되도 록 디자인하였다. [Fig. 3]의 그림을 순서대로 보면 동력원이 회전할 때 연결된 조인트도 같이 회전하며, 조인트의 움직임 에 따라 모든 링크들이 유기적으로 각각의 움직임을 가져는 것을 알 수 있다.
결론적으로 본 로봇의 다리는 3쌍의 4절 링크가 하나의 다 리를 구성하고 다리 하나가 1 자유도를 가지도록 설계되어, 하 나의 동력원만으로도 다리 전체가 교차적 움직임을 수행할 수 있도록 하였다. 로봇 전체적으로는 양쪽 다리가 위와 같은 움 직임을 반복하여 삼각의 교차적 움직임(tripod alternating gait) 를 형성한다.
2.2 다리 경로 디자인
크롤링 로봇의 성공적인 주행 조건으로 교차적 다리 움직 임 뿐만 아니라, 발의 경로 역시 중요하다. 로봇이 주행하기 위 해서는 지면에 닿은 상태에서 로봇을 앞으로 밀어줄 수 있는 추진력이 필요한다. 교차적 움직임으로 공중에 뜨는 위상 (aerial phase)을 만들어 주더라도 앞으로 밀어주지 못한다면 로봇은 제자리에 머무를 수 밖에 없다. 또한, 다리의 경로에 따 라 로봇이 움직이는 방향이 달라진다. 따라서 본 로봇은 발이 땅을 미는 모션을 위하여, 발이 타원형에 가까운 경로를 따르 도록 디자인 하였다.
[Fig. 4]는 다리가 움직일 때 나타나는 발의 경로를 보여준 다. 주행성을 높이려면 땅을 미는 모션이 비교적 길게 나타나 야 한다. [Fig. 4]에서 세 발의 경로 모두 타원형에 가까운 것을 볼 수 있으며, 상하 움직임([Fig. 4 (a)]의 A) 보다는 좌우의 길 이([Fig. 4 (a)]의 B)가 긴 것을 알 수 있다. 납작한 타원형의 경 로를 통해 로봇은 앞으로 움직일 수 있는 추진력을 충분히 얻 을 수 있다.
3. 다리 경로 분석
앞서 논의한 바와 같이, 원활한 크롤링 모션을 구현하기 위 해서는 공중에 뜨는 위상(aerial phase)과 추진력(thrust force) 을 적절히 만들어내는 것이 중요하다. 이를 가능케하기 위해 본 논문에서는 타원형의 다리 경로를 설계하였고, 모델링을 통해 심층적으로 분석하였다.
[Fig. 5]는 가운데 4절 링크와, 오른쪽 4절 링크의 모식 도를 나타낸다. 위 4절 링크를 기반으로 위치 해석을 수행 하면 다음과 같은 식을 얻을 수 있다. 식 (1), (2)는 오른쪽 4절 링크, 식 (3), (4)는 가운데 4절 링크의 기하학적 관계 를 나타낸다.
| (1) |
| (2) |
| (3) |
| (4) |
식(1)-(4) 연립하여 링크의 현재 위치들을 모두 알 수 있으 며, 이를 바탕으로 발의 경로를 계산할 수 있다. 발의 경로는 식(5)와 (6)으로 주어진다. 식(5)는 가운데 발의 위치인 A점, 식 (6)은 오른쪽 발의 위치인 B점을 나타낸다.
| (5) |
| (6) |
3. 실험 및 결과
3.1 실제 로봇의 다리 위상 차이 및 경로 확인
크롤링 로봇의 주행 조건을 만족시키기 위해 공중에 뜨는 위상(aerial phase) 생성을 위한 다리의 교차적 움직임과 추진 력 발생을 위한 다리 경로를 모델링과 실험을 통해 확인한다. [Fig. 6]는 모델링과 실험으로 얻어진 발의 경로를 보여준다. 왼쪽 발의 경우 오른쪽 발과 대칭적으로 디자인 되었기 때문 에 중간 발과 오른쪽 발에 대해서만 비교를 하였다.
[Fig. 6 (a), (b)]에 나타난 것처럼, 실험 데이터와 모델링 데이터 모두 비슷한 형태의 경로를 보인다. 납작한 타원 형의 모습을 가지며, 로봇을 공중에 띄울 수 있는 상하 움 직임이 비교적 짧게 나타난다. 반대로, 로봇을 앞으로 밀 어줄 수 있는 좌우 움직임이 비교적 길게 나타난다. 이와 같이 설계된 발의 경로에 의해 로봇은 공중에 띄워지고, 추진력을 통해 앞으로 움직일 수 있다.
그러나 위상차에 있어서는 정반대의 움직임을 보인다. [Fig. 6 (b)]의 실험 데이터에서는 발의 위상을 시간에 따라 다 른 색깔로 나누어 표현하였다. 데이터와 같이 가운데 발이 지 면과 닿아 박차고 나갈 때, 오른쪽 발은 허공에서 움직이며 다 시 땅을 밀어줄 준비를 한다. 반대로, 오른쪽 발이 땅에 닿을 경우에는 가운데 발이 허공에 위치한다. 이와 같이 정 반대의 위상차를 나타내며, 두 다리가 교차적으로 움직이면서 연속적 으로 땅을 계속 치게 된다. 이는 간헐적으로 로봇을 공중으로 띄우는 상태를 발생시켜, 원활한 주행을 가능하게 한다.
3.2 주행 테스트
모델링에 따른 경로 디자인을 실제 로봇에 적용하여주행 테스트를 수행하였다. 주행 테스트에서는 크게 두 가지를 확 인하고자 하였다. 우리는 오픈 소스 비디오 분석 프로그램인 키노베아(Kinovea) 를 활용하여 질량 중심의 수직 방향 위치 변화와 수평 방향 이동 거리[11]를 조사하였다.
로봇의 주행 중 수직 위치 변화는 적을수록 안정적이며[12], 심한 위치 변화는 에너지 효율 측면에서 주행성을 떨어뜨린 다. 뿐만 아니라, 동적 안정성에도 악영향을 미쳐 로봇의 전복 가능성을 증해 시킬 수 있다. [Fig. 7]은 시간에 따른 질량 중심 의 수직 위치 변화를 나타낸다. 그래프에서 보듯이 대략적인 사인파의 형태를 나타내고 있으며, 진폭은 약 5 mm 내외로 로 봇은 수직 방향으로 큰 위치변화없이 주행한다. 즉, 6개의 발 이 교차적인 삼각 걸음걸이(tripod gait)를 형성하면서 로봇을 공중에 간헐적 또는 연속적으로 띄우게 되는데, 그 띄우는 높 이를 어느 정도 일정하게 유지시켜주고 있다는 뜻으로 해석할 수 있다. 뿐만 아니라, 수직 높이를 일정하게 함으로써 로봇이 고속에서도 안정성을 잃지 않고 주행할 수 있게 된다.
[Fig. 8]은 로봇의 주행 스피드를 측정하기위해 시간대 비 수평 이동 거리를 나타낸 것이다. [Fig. 8]에서 기울기 를 측정한 결과, 로봇은 약 0.9 m/s의 주행 스피드를 보여 주며, 이는 대략 8 body length/s의 몸 길이 대비 속력이다. [Table 1]에서의 다른 크롤링 로봇들과 비교하여 중간 정도 의 속력을 가짐을 알 수 있다.
[Fig. 9]은 실제 크롤링 로봇의 주행 모습을 보여준다. 연 속 주행 장면에서 볼 수 있듯이 로봇 몸체의 수직 위치 변화 는 약 5 mm 정도 내외로 크지 않다. 또한, 0.4초 동안 약 360 mm 정도를 이동하여 고속 주행이 가능함을 확인하였다.
3.3 Discussion
본 로봇은 한 쌍의 다리를 양 쪽에 가지며, 양 쪽 다리는 각 각 세 개의 발을 가지고 있다. 세 개의 발은 3쌍의 4절 링크로 연결되어 하나의 모터를 통해 항상 함께 움직이도록 설계되었 다. 즉, 본 로봇은 총 2개의 DC 모터를 통해 좌우의 다리를 독 립적으로 제어할 수 있다. 따라서 좌우 DC모터의 회전 속도를 다르게 제어하면 각 다리의 구동 속도를 제어할 수 있고, 이에 따라 로봇은 방향 전환이 가능하다. 현재는 PWM (pulse width modulation) 신호를 통해 양 다리의 구동 속도만 동일하게 제 어하고 있으며, 중요하다고 생각되는 위상 차이는 제어하지 않고 있다.
고속 카메라 촬영을 통해 비디오를 분석해보면, 로봇이 정 확하게 삼각의 교차적 움직임(tripod alternating gait)를 보여주 지는 않는다. 그러나 대부분의 경우 tripod alternating gait에 가 까운 형태를 보여주고 있으며, 이 덕분에 질량 중심의 수직 위 치 변화가 어느 정도 작게 유지되고 있는 것으로 추정된다. 추 후에는 다리의 위상 상태 센싱 또는 모터 제어를 통해 위상 차 이에 따른 로봇의 gait 변화, 수직 및 수평 움직임 변화 등의 조 사가 필요하다고 생각된다. 이는 본 크롤링 로봇 뿐만 아니라 크롤링 로코모션(locomotion) 자체를 이해하는 데에 도움이 될 것이라 생각한다.
4. 결 론
본 논문에서는 소형, 경량의 6족 크롤링 로봇을 제안하였 다. 소형 크롤링 로봇의 필수 조건인 교차적 다리 움직임 (alternating gait)과 모든 다리가 공중에 위치할 수 있는 위상 (aerial phase)을 1자유도 planar linkage 디자인을 통해 달성하 였다. 로봇은 2개의 다리를 가지며, 각 다리는 3개의 발을 가진 다. 3개의 발은 기구학적 디자인에 따라 교차적인 움직임을 보인 다. 이러한 다리를 양 옆으로 배치하여 자연스러운 alternating tripod gait를 생성할 수 있도록 하였다. 또한 모델링을 통해 교 차적 움직임을 극대화 하였고, 주행 테스트를 통해 실제 다리 의 교차적 움직임을 확인할 수 있었다.
Acknowledgments
This study was financially supported by Seoul National University of Science & Technology.
References
- L. H. Ting, R. Blickhan, R. J. Full, “Dynamic and static stability in hexapedal runners”, Journal of Experimental Biology, (1994), 197, p251-269.
-
A.M. Hoover, E. Steltz, R.S. Fearing, RoACH: An autonomous 2.4g crawling hexapod robot, 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems, Nice, France, p26-33, (2008).
[https://doi.org/10.1109/iros.2008.4651149]

-
R.J. Wood, S. Avadhanula, R. Sahai, E. Steltz, R.S. Fearing, Microrobot Design Using Fiber Reinforced Composites., J. Mech. Des., (2008), 130, p052304.
[https://doi.org/10.1115/1.2885509]

-
P. Birkmeyer, K. Peterson, R.S. Fearing, DASH: A dynamic 16g hexapedal robot, 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems, St. Louis, MO. USA, p2683-2689, (2009).
[https://doi.org/10.1109/iros.2009.5354561]

-
D.W. Haldane, K.C. Peterson, F.L.G. Bermudez, R.S. Fearing, Animal-inspired Design and Aerodynamic Stabilization of a Hexapedal Millirobot, 2013 IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, p3279-3286, (2013).
[https://doi.org/10.1109/icra.2013.6631034]

-
D.W. Haldane, R.S. Fearing, Running beyond the bio-inspired regime, 2015 IEEE International Conference on Robotics and Automation, Seattle, WA, USA, (2015).
[https://doi.org/10.1109/icra.2015.7139828]

- A.T. Baisch, R.J. Wood, Pop-up Assembly of a Quadrupedal Ambulatory MicroRobot_HARM, 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, (2013).
-
A.T. Baisch, O. Ozcan, B. Goldberg, D. Ithier, R.J. Wood, High speed locomotion for a quadrupedal microrobot., Int. J. Robot. Res., (2014), 33, p1063-1082.
[https://doi.org/10.1177/0278364914521473]

-
A.T. Baisch, C. Heimlich, M. Karpelson, R.J. Wood, HAMR3: An autonomous 1.7g ambulatory robot, 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, p5073-5079, (2011).
[https://doi.org/10.1109/iros.2011.6095063]

-
J-E. Lee, G-P. Jung, K-J. Cho, Bio-inspired Design of a Double-Sided Crawling Robot, Conference on Biomimetic and Biohybrid Systems, vol. 10384, Stanford, CA, USA, p562-566, (2017).
[https://doi.org/10.1007/978-3-319-63537-8_50]

-
Y. Lee, J. Park, Real-Time Force Control of Biped Robot to Generate High-Speed Horizontal Motion of Center of Mass., Journal of Korea Robotics Society, (2016), 11(3), p183-192.
[https://doi.org/10.7746/jkros.2016.11.3.183]

-
J. Piao, J. Jung, X. Jin, S. Park, J-O. Park, S.Y. Ko, Vibration Analysis of Planar Cable-Driven Parallel Robot Configurations., Journal of Korea Robotics Society, (2016), 11(2), p73-82.
[https://doi.org/10.7746/jkros.2016.11.2.073]