입자 크기의 구성 비율에 따른 휨강성 최적화 가능성의 탐구
© Korea Robotics Society. All rights reserved.
Abstract
As an interpretation of existing jamming effects, the main variables affecting the increase in stiffness due to jamming are known as system density, jamming density, pressure, and particulate temperature. The main variable, jamming density, is closely related to the distribution of particle size and contact properties such as particle shape and friction. However, the complexity of these variables makes it difficult to fully understand the mechanism of the jamming effect. In this paper, we focus on the jamming effects of particles that have more elastic properties than particles such as sand and coffee powder, which are commonly used as constituent particles of existing jamming, in order to reduce complicated factors such as temperature and concentrate on jamming effects based on elastic characteristics of particles. It was experimentally explored the possibility of increasing stiffness by mixing particles of different sizes rather than simply increasing the bending stiffness by controlling the particle size. Through simulations and experiments, we found a case where the stiffness of each particle size distribution is larger than the stiffness of each particle size.
Keywords:
Variable-stiffness, Jamming Effect, Mixture, Size Distribution1. 서 론
최근에는 기존의 하드 로봇의 단점을 극복하기 위해 소프트 로봇에 대한 연구가 활발히 진행되고 있다. 하드 로봇은 일반적인 환경에서 정밀하게 구동 될 수 있다는 이점이 있지만 제조 방법 및 제어 논리가 복잡하고 어렵 다. 또한 딱딱한 재질로 되어 있어 구조 변형이 어렵기 때문에 비정형 환경에서 구동하기에 부적합하다. 반면, 소프트 로봇은 부드러운 소재로 만들어져 비정형 환경 에서도 구조적으로 변형되어 효과적으로 작동 할 수 있 게 된다. 따라서 소프트 로봇은 불안정한 환경에서 장애 물을 극복 할 수 있어, 인간과의 직접적인 상호 작용이 요구되는 환경인 의료 산업 및 재난 로봇에 사용할 수 있다.
소프트 로봇의 재질 특성으로 인해, 설계되지 않은 환 경에서도 유연하게 대처할 수 있지만, 반면에 작은 강성 때문에 설계된 작업을 수행하는 데 부족함이 있다. 앞서 기술한 의료 산업 및 재난 로봇에 사용되기 위해서는 소프트 로봇의 강성을 조절하여 소프트 로봇이 외력에 저항 할 수 있도록 해야 한다. 이에 따라 다양한 강성 조절 메커니즘들(variable-stiffness mechanism)이 개발 되어 왔다[1-3].
본 논문에서는 재밍 효과를 사용한 소프트 로봇의 휨 강성(bending stiffness) 증가에 기여하기 위해 재밍 효과 의 강성 증가에 대한 연구를 진행하였다. 자세히 기술하 면, 서로 다른 크기를 갖는 두 입자의 구성 비율인 입자 크기 분포(particle size distribution)에 따른 강성 추이를 시뮬레이션과 실험을 통해 탐구하였다.
2장에서는 소프트 로봇의 강성 조절 메커니즘에 대한 연구들을 소개하며, 3장에서는 시뮬레이션을 수행하기 위한 해석 배경 및 목표, 역학적 분석과 주요 변수의 설 정 과정을 제시하였다. 4장에서는 시뮬레이션의 수행과 결과를 제시하였고, 5장에서는 이론과 시뮬레이션을 검 증하기 위한 실험이 다뤄진다. 마지막으로, 시뮬레이션 과 실험의 결과를 해석 및 정리하였다.
2. 관련 연구
이 장에서는 소프트 로봇의 강성 조절 메커니즘에 관 련된 연구들을 살펴본다.
2.1. 최근 가변 강성 메커니즘
연성 로봇의 개발을 위해 액추에이터(actuator), 센서 및 제어 기술과 같은 다양한 분야에서 연구가 진행되고 있다. 이 중 가변 강성 메커니즘은 소프트 로봇의 개발에 서 가장 중요한 부분이다[4]. 소프트 로봇에 적용되는 가 변 강성 메커니즘의 경우 로봇 자체가 변형되지 않는 상태에서 강성을 조정해야 하기 때문에 적용 할 수 있는 기술에는 한계가 있다. 따라서 로봇 자체의 변형을 일으 키지 않고 강성을 변화시킬 수 있는 형상 기억 물질, 재 밍 등을 이용한 기술이 적용되어 왔다.
2.2. 입자상 재밍 효과
입자상 재밍(granular jamming)은 얇은 막에 작은 입 자가 차 있는 구조에서 일어난다. 일반적으로 작은 입자 로 인해 액체와 같은 거동을 하나, 음압이 가해지면 막과 입자 사이의 상호 작용으로 강성이 증가한다. 이렇게 강 성이 증가하는 현상을 이용하여 소프트 로봇 분야에 다 양하게 적용된다. 적용 분야로서는, 그리퍼(gripper)에 처음으로 적용되었으며, Fig. 1에 나타난 스티프-플롭 (stiff-flop)과 같은 수술 로봇의 가변 강성 메커니즘으로 도 적용되었다[4,5,12]. 입자상 재밍 효과를 사용하는 가변 강성 메커니즘은 반응 속도가 빠르고 효과적이라는 점 에서 유리하다. 그러나 재밍 효과에 의한 강성의 증가 정도가 다른 방법보다 좁으며 정확한 작동 원리는 명확 하지 않는 것이 단점이다[6]. 재밍 효과에 있어 중요한 역할을 하는 막에 대한 연구도 있었다. 라텍스, 비닐 등 의 재질을 사용하여 막이 강성에 어떤 영향을 미치는 가에 대해서 연구가 진행되었다[11]. 또한 구성 입자의 모 양에 따른 재밍 효과에 대한 연구 또한 진행되었다[14].
3. 모델 분석
이 장에서는 실험의 최적화를 위한 모델의 역학적 분 석을 수행하고 실험을 위한 가설을 제시한다.
기존 재밍 효과에 대한 해석으로서, 재밍에 의한 강성 증가에 미치는 주요한 변수는 시스템 밀도, 재밍 밀도, 압력, 입자상 온도라고 알려져 있다. 주 변수인 재밍 밀 도는 입자 크기의 분포와 입자 모양과 마찰과 같은 접촉 특성과 깊은 관련이 있다[7-9]. 따라서 재밍 효과에 큰 영 향을 주는 변수는 입자 특성, 압력과 입자상 온도라고 볼 수 있다.
그러나 이러한 변수들이 복잡하게 얽혀있어 재밍 효 과의 매커니즘을 온전히 이해하기 힘든 실정이다. 이에 이 논문에서는 온도 등 복잡한 요인을 줄이고 입자의 탄성 특징에 기초한 재밍 효과에 집중하기 위해 기존 재밍의 구성 입자로 많이 쓰이는 모래와 커피 가루 같은 입자보다 탄성의 특징을 가지고 있는 입자, 쉽게 접할 수 있는 구형 스티로폼 입자에 대한 재밍 효과에 대한 분석을 진행하려 한다.
연구의 목표는 단순히 입자 크기의 조절로 휨강성을 증가시키는 효과보다, 서로 다른 크기의 입자를 섞음으 로써 강성을 더 크게 증가시킬 수 있는 가능성에 대한 탐구이다. 입자의 크기가 달라짐에 따라 재밍에 의한 강 성은 단순 증가, 감소 함수로 나타날 것이다 그러나 각각 의 해당 입자 크기에 의한 강성보다 입자 크기 분포가 있을 경우의 강성이 더 클 수 있다는 예측에 착안하여 이 연구를 진행하였다. 이에 서로 다른 크기의 입자 비율 분포인 입자 크기 분포(particle size distribution)을 제어 변수로 선택하여 강성 측정 시뮬레이션과 실험을 진행 하였다.
4. FEM 시뮬레이션
이 장에서는 시뮬레이션의 목표와 진행에 필요한 변 수의 설정, 진행 및 결과를 소개한다.
4.1. 시뮬레이션 목표와 설정
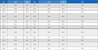
이 시뮬레이션은 두 개의 서로 다른 지름을 갖는 구형 입자들(spherical particles)을 갖고 진행된다. 그리고 이 입자들을 질량 비율로 섞어 만든 케이스들을 라텍스 막 (latex membrane)으로 둘러싼다. 막의 두께는 4 mm, 막 의 단면의 지름은 24 mm이고, 막의 길이는 140 mm으로 설정하였다. 입자의 크기로는 지름 18.5 mm의 ball 1과 10 mm의 ball 2를 사용하였다. 두 입자의 밀도는 30 kg/m3와 포아송 비는 0.5로 같다. 구형 스티로폼의 영률 은 50 kPa, 라텍스 막의 영률은 10 kPa로 설정하였다. 두 입자와 막과 입자 사이의 최대 정지 마찰계수는 0.5로 설정하였다. 각 실험 케이스는 ball 1 (B1)과 ball 2 (B2) 의 질량 비율을 달리해 Table 1과 같이 시뮬레이션 경우 를 6가지로 세분화하였다.
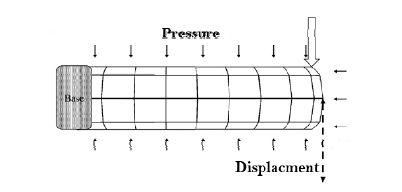
Fig. 2는 시뮬레이션으로 실행할 구조를 나타낸 것이 다. Abaqus 프로그램을 사용하여 Fig. 2와 같이 기저를 제외한 부분에 균일한 압력 60 kPa을 가하였다. 그리고, 일정한 힘 10 gf이 막의 꼭대기 부분에 -y 방향으로 가해 끝 단의 변위를 얻었다. 그 변위는 재밍 효과의 강성 증 가 메커니즘의 강성 증가의 정도를 결정하기 위해 사용 된다.
4.2. 시뮬레이션 방법
시뮬레이션의 모델은 Fig. 3와 같다.
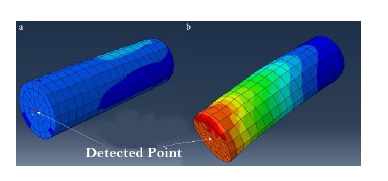
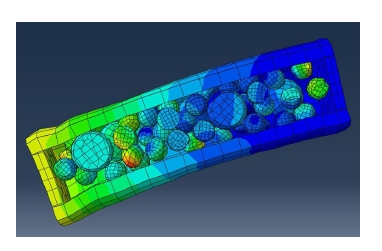
Solidworks 프로그램을 사용하여 모델을 Fig. 3과 같 이 만든 뒤, Abaqus에 적용하였다. 각각의 경우에 같은 힘을 주어 생긴 변위를 Fig. 4과 같이 측정하였다. 구조 해석 프로그램 Abaqus를 사용해 얻은 단면도는 Fig. 5과 같다.
4.3. 시뮬레이션 결과
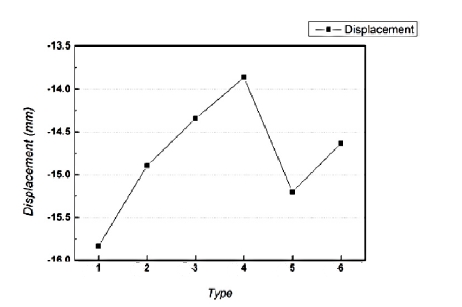
이 시뮬레이션에서 얻은 끝 단의 변위가 작을수록 재 밍 효과가 효과적으로 일어났다고 간주한다. 6가지로 나 눈 경우들에 대한 각각 변위는 Fig. 6과 같다.
1번 케이스와 6번 케이스를 비교해보면, 단일 크기 입 자의 재밍 강성의 경우 입자의 지름이 작을수록 컸음을 알 수 있다. 그러나 단일 크기의 입자로만 구성한 1, 6번 케이스보다 입자 크기 분포가 존재하는 4번 케이스의 경우의 강성이 더 큰 것을 확인할 수 있다. 이는 입자 크기 분포로 재밍 강성을 최적화 할 수 있다는 가능성을 보여준다. 그렇지만 2번과 5번 케이스의 결과에 의하면 입자 크기 분포에 의한 강성이 오히려 단일 입자 크기에 의한 강성보다 줄어들 수 있다는 결과를 보여주고 있다. 이에 대한 해석은 아래 진행된 실험 결과와 같이 다룰 것이다.
5. 실 험
5.1. 실험 구성
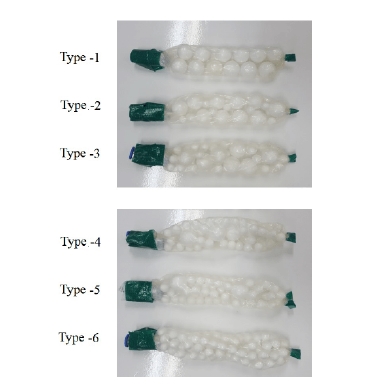
실험은 시뮬레이션의 결과를 검증하기 위해 진행되었 다. 실험을 진행하기 위한 구성품은 Fig. 7과 같이 a) 얇 은 라텍스 막 b) 크기가 다른 구형 스트로폼 c) 음압을 제공하기 위한 공압 연결부 d) 부직포로 구성되었다. 라 텍스 막을 제외한 나머지 조건과 물성치는 모두 시뮬레 이션의 것과 동일하다. 실험 모델은 Fig. 8과 같이 제작 하였다.

Components of soft robot model a) a thin latex membrane, b) shperical particle of two different radius, c) a pnuematic connector for giving a negative pressure, d) a nonwoven fabric
실험은 Fig. 9과 같이 진공 펌프를 통해 60 kPa에 달하 는 음압을 소프트 로봇에 가하고, 소프트 로봇의 끝 단에 10 gf에 해당하는 일정한 힘을 가해주어 끝 단의 변위를 줄자를 통해 측정하였다. 이 실험은 앞서 Table 1에서 언급된 각 케이스에 대해 세 번 반복되었다.
5.2. 실험 결과
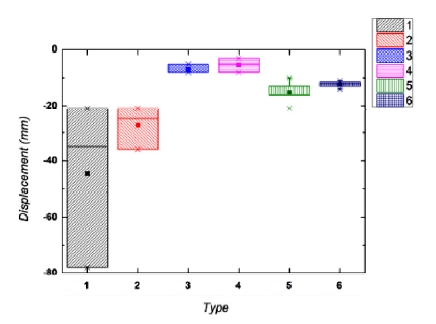
세 번의 실험을 통하여 얻은 변위의 값을 나타낸 막대 그래프와 변위의 평균값을 그래프로 정리하면 Fig. 10 과 같다.
시뮬레이션과 마찬가지로 실제 실험에서도 4번 케이 스의 강성이 가장 좋은 결과를 보였다. 또한 4번과 5번 케이스는 입자 크기 분포의 조절로 인해 강성 관점에서 이득을 본 것도 마찬가지이다. 2번과 5번 케이스에 관해 서도 단일 입자 크기에 의한 강성보다 낮게 나올 수 있다 는 결과가 도출되었다.
다른 타입의 실험과는 다르게, 첫 번째 타입의 변위의 변동이 가장 크게 나왔다. 이는 강도가 낮은 스티로폼을 사용하여 반복되는 실험에 의한 영구적 변형에 의한 변 위의 증가로 보여진다. 또한 재밍 효과를 효과적으로 확 인하기 위해 필요한 입자 수가 충분치 못해 발생하는 오차이기도 하다.
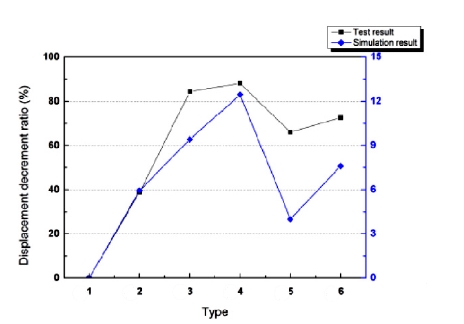
Fig. 11는 시뮬레이션 실험과 실제 실험의 데이터 추 이를 비교한 그래프이다. 시뮬레이션과 실험의 결과는 4번 케이스, 큰 입자 대 작은 입자의 질량비가 40 : 60인 경우 가장 큰 강성 증가를 보였다는 점에서 동일한 결과 를 보였다. 그러나 시뮬레이션 결과의 경우 실제 실험의 결과에 비해서 변화의 폭이 매우 작다. 이는 시뮬레이션 의 모델 중 라텍스 막의 두께가 실제 모델의 막의 두께와 큰 차이를 보이기 때문인 것으로 파악된다.
6. 결 론
본 논문의 목적은 단순히 입자 크기의 조절로 휨강성 (bending stiffness)을 증가시키는 효과보다, 서로 다른 크 기의 입자를 섞음으로써 강성을 더 크게 증가시킬 수 있는 가능성에 대해 실험적으로 탐구하는 것이었다. 시 뮬레이션과 실험을 통해 각각의 해당 입자 크기에 의한 강성보다 입자 크기 분포가 있을 경우의 강성이 더 큰 케이스를 발견하였다. 다시 기술하면, 서로 다른 크기의 입자 비율 분포인 입자 크기 분포(particle size distribution) 를 제어 변수로 선택하여 강성을 증가시키는 방법이 존 재함을 보였다.
앞으로의 연구 진행 방향은 다음과 같다. 우선적으로, 입자 크기 분포에 의한 강성 증가의 원인을 규명하는 것 이다. 원인을 설명할 수 있는 한 가지 예로, 입자 간 힘의 전달을 표현하는 연쇄힘(force chain)을 들 수 있다[10,13]. 크기가 다른 입자 간의 연쇄힘의 특징을 탐구하면 원인 을 발견할 수 있을 것이다. 또한 본 논문에서 다루는 주 제가 강성이므로, 해당 연쇄힘에 의한 변형을 무시할 수 없다. 연쇄힘과 연쇄힘에 의한 변형의 관계를 탐구하면 강성 증가의 원인을 규명할 수 있을 것으로 판단된다.
두번째로, 주어진 입자 크기에 대해 어떤 입자 크기 분포를 구성해야 최적의 강성 증가를 얻을 수 있을 지에 대한 구체적인 연구이다. 이를 달성하기 위해서는 discrete element method (DEM) 등을 통한 가상 해석을 이용할 수 있을 것이다. 이를 사용하여 입자의 배치를 손 쉽게 다양하게 배치하여 보다 신뢰적인 데이터 취득에 도움 이 될 것으로 보인다.
그밖에 다양한 하중에 대한 데이터를 취득하여 stressstrain 그래프를 얻어 세밀한 분석을 수행해야 할 것이다. 이에 더해 스티로폼 같이 강도가 낮은 입자 대신에, 보다 뛰어난 물성을 갖는 입자를 통해 다양한 시험 데이터를 취득한다면 분석에 도움이 될 것이다. 이러한 데이터를 바탕으로 재밍 효과 중 강성 증가를 설명하는 적절한 입자간 상호작용을 제시하는 것이 궁극적 목표이다.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 20162016R1A 2B4009858)
References
-
Hannan, M., Walker, I., Kinematics and the implementation of an elephant’s trunk manipulator and other continuum style robots, J. Robot. Syst, (2003), 20(2), p45-63.
[https://doi.org/10.1002/rob.10070]

-
Laschi, C., Mazzolai, B., Mattoli, V., Cianchetti, M., Dario, P., Design of a biomimetic robotic octopus arm, Bioinspir. Biomim, (2009), 4(1), p015006.
[https://doi.org/10.1088/1748-3182/4/1/015006]

-
Cianchetti, M., Arienti, A., Follador, M., Mazzolai, B., Dario, P., Laschi, C., Design concept and validation of a robotic arm inspired by the octopus, Mater. Sci. Eng. C, (2011), 31(6), p1230-1239.
[https://doi.org/10.1016/j.msec.2010.12.004]

-
Manti, M., Cacucciolo, V., Cianchetti, M., Stiffening in soft robotics: a review of the state of the art, IEEE Robot. Autom. Mag, (2016), 23(3), p93-106.
[https://doi.org/10.1109/mra.2016.2582718]

-
Ranzani, T., Cianchetti, M., Gerboni, G., Falco, I., Menciassi, A., A soft modular manipulator for minimally invasive surgery: design and characterization of a single module, IEEE Trans. Robot, (2016), 32(1), p187-200.
[https://doi.org/10.1109/tro.2015.2507160]

-
Cheng, N.G., Lobovsky, M.B., Keating, S.J., Seatapen, A.M., Gero, K.I., Hosoi, A.E., Design and analysis of a robust, low-cost, highly articulated manipulator enabled by jamming of granular media, IEEE International Conference on Robotics and Automation, (2012), Cambridge, United States.
[https://doi.org/10.1109/icra.2012.6225373]

-
Majmudar, T., Sperl, M., Luding, S., Behringer, R., Jamming transition in granular systems, Phys. Rev. Lett, (2007), 98(5).
[https://doi.org/10.1103/physrevlett.98.058001]

-
Corwin, E., Jaeger, H., Nagel, S., Structural signature of jamming in granular media, Nature, (2005), 435(7045), p1075-1078.
[https://doi.org/10.1038/nature03698]

-
Chen, D., Torquato, S., Confined disordered strictly jammed binary sphere packings, Phys. Rev. E, (2015), 92(6).
[https://doi.org/10.1103/physreve.92.062207]

-
Peters, J., Muthuswamy, M., Wibowo, J., Tordesillas, A., Characterization of force chains in granular material, Phys. Rev. E, (2005), 72(4).
[https://doi.org/10.1103/physreve.72.041307]

-
Jiang, A., Ranzani, T., Gerboni, G., Lekstutyte, L., Althoefer, K., Dasgupta, P., Nanayakkara, T., Robotic granular jamming: Does the membrane matter?, Soft Robotics, (2014), 1(3), p192-201.
[https://doi.org/10.1089/soro.2014.0002]

-
Brown, E., Rodenberg, N., Amend, J., Mozeika, A., Steltz, E., Zakin, M., Lipson, H., Jaeger, H., Universal robotic gripper based on the jamming of granular material, Proc. Natl. Acad. Sci. USA, (2010), 107(44), p18809-18814.
[https://doi.org/10.1073/pnas.1003250107]

-
Hidalgo, R.C., Herrmann, H.J., Parteli, E.J., Kun, F., “Force chains in granular packings,” inProceedings-International School Of Physics Enrico Fermi, vol. 155, Ohmsha, (2004), 1999, p153-172.
[https://doi.org/]

-
Athanassiadis, A.G., Miskin, M.Z., Kaplan, P., Rodenberg, N., Lee, S.H., Merritt, J., Jaeger, H.M., Particle shape effects on the stress response of granular packings, Soft Matter, (2014), 10(1), p48-59.
[https://doi.org/10.1039/c3sm52047a]

2016 성균관대학교 기계공학부(공학사)
2017~현재 성균관대학교 기계공학부(공학 석사 과정)
관심분야: 소프트 로봇의 가변 강성 메커니즘, 칼만 필터, Serial Elastic Actuator
1996 포항공과대학교 기계공학과(공학사)
1998 포항공과대학교 기계공학과(공학석사)
2005 Mechanical Engineering from the University of Michigan(공학박사)
2005~2007 Carnegie Mellon Univ. Post‐doctoral Fellow
2008~현재 성균관대학교 기계공학부 교수
관심분야: Robotic manipulation, hydraulic robots, SLAM, mobile robot navigation, polymer-based sensors and actuators
1984 서울대학교 기계공학과(공학사)
1986 KAIST 기계공학과(공학석사)
1994 포항공과대학교 기계공학과(공학박사)
1986~1989 LG전자 정보기술 연구소 주임연구원
1993~1995 일본정부 문부성 초청 동경대학 연구원
1999~2000 일본 AIST 초빙 연구원
1995~현재 성균관대학교 기계공학부 교수
관심분야: Dexterous mechanism, field application of robots and soft mechatronics