[ ARTICLE ]

The Journal of Korea Robotics Society - Vol. 12, No. 2, pp.194-205

ISSN: 1975-6291 (Print) 2287-3961 (Online)

Print publication date May 2017

Received 11 Jan 2017 Revised 14 Apr 2017 Accepted 24 Apr 2017

DOI: https://doi.org/10.7746/jkros.2017.12.2.194

평면형 3자유도 병렬 메커니즘의 여유 구동 특성 분석

전정인¹ ; 오현석¹ ; 우상훈¹ ; 김성목¹ ; 김민건² ; 김희국^†

Analysis of the Redundant Actuation Characteristics of the Planar 3-DOF Parallel Mechanism

Jung In Jeon¹ ; Hyun Suk Oh¹ ; Sang Hun Woo¹ ; Sung Mok Kim¹ ; Min Gun Kim² ; Whee Kuk Kim^†

1Electro-Mechanical System Engineering, Korea University at Sejong darkas2000@korea.ac.krmozozo@korea.ac.krsang-hun.woo@kr.abb.comsungmok.kim@kohyoung.com
2Advanced Mechanical Engineering, Kangwon National University mgkim@kangwon.ac.kr

†Corresponding author : Electro-Mechanical System Engineering, Korea University at Sejong, Korea ( wheekuk@korea.ac.kr)

Abstract

A redundantly actuated planar 3-degree-of-freedom parallel mechanism is analyzed to show its high application potential as a haptic device. Its structure along with the closed form forward position solutions is briefly discussed. Then its geometric and kinematic characteristics via singularity analysis, the kinematic isotropy index, and the input-output force transmission ratio are investigated both for the redundantly actuated cases and for the non-redundantly actuated case. In addition, comparative joint torque simulations of the mechanism with different number of redundant actuations as well as without redundant actuation are conducted to confirm the improved joint torque distribution characteristics. Through these analyses it is shown that the geometric and kinematic characteristics of the redundantly actuated mechanism are superior to the ones of the mechanism without redundant actuation. Thus, it can be concluded that the suggested planar mechanism with redundant actuation has a very high potential for haptic device applications.

Keywords:

Redundant Actuation, Parallel Mechanism, Singularity Analysis, Kinematic Characteristics, Haptic device

1. 서 론

병렬 메커니즘은 외팔보의 형태를 가지는 하나의 체 인으로 구성되는 직렬 메커니즘과는 달리 출력판 (또는 운동판)이 다수의 부속체인으로 지지되는 구조이므로 직렬 메커니즘에 비하여 작업공간은 상대적으로 작지만 정밀도와 강성 측면에서는 우수한 특성을 나타내며 또 한, 무거운 모터를 지면 가까이 배치함으로써 낮은 관성 은 물론 중력 효과를 최소화 할 수 있는 장점이 존재한다. 특히, 병렬 메커니즘의 병렬 특이형상은 이들 부속 체인 간의 구속조건으로 인해 발생되며 유용한 작업공간의 크기를 더욱 제한하는 요소중의 하나이다. 따라서, 이들 병렬 특이형상에 대한 분석 또는 이들 특이형상을 회피 할 수 있는 방안에 대한 연구는 매우 중요한 문제중의 하나로 인식되고 있다.

하지만, 병렬 메커니즘의 경우 여유구동을 활용하게 되면 특이형상 회피는 물론 기구학 특성, 최대 출력 하 중, 그리고 고장에 대한 강인성 등을 개선할 수 있는 이 점이 있다. 따라서, 이러한 여유구동 특성을 효과적으로 활용하는 다양한 병렬 구조 메커니즘에 대한 특성 분석 이 수행되었으며 이와 더불어 최소 놈에 기반한 기법과 다수의 목적 함수에 우선 순위를 부여하는 기법 등 다양 한 여유구동 알고리즘이 제시되었다^[1-8].

병렬 메커니즘의 특이형상의 분석은 일반적으로 부속 체인의 구조로부터 발생되는 직렬 특이형상과 구동관절 에 의해 운동판에 가해지는 구동렌치들간의 비독립성으 로 발생되는 병렬 특이형상이 있다. 이들에 대한 분석을 위해서는 해당 행렬의 디터미넌트가 영이 되는 조건으 로부터 구하는 기법^[9]과 Grassmann Line Geometry (GLG) 기법^[9,10], 그리고 Grassmann Cayley Algebra 기 법^[11-13] 등이 활용되고 있다. 특히, 평면형 메커니즘의 경우와 같이 구조가 단순한 경우 GLG 기법을 통하여 대부분의 특이형상을 규명할 수 있다^[9,10].

병렬 메커니즘의 기구학 특성 분석은 자코비안의 최 소 특이값이나 최대 특이값, 또는 최소-대-최대 특이값 으로 정의되는 기구학 등방성지수가 사용되고 있으나 기구학 등방성지수의 경우 작업공간내의 형상에서 모든 방향으로 입출력 속도 전달비가 얼마나 균일하게 전달 되는 가를 나타내므로 일반적인 기구학 특성을 표현하 는 목적으로 사용된다^[14-19]. 병렬 메커니즘의 입출력 특 성 분석은 최소 입출력전달비나 최대 입출력전달비, 또 는 최소-대-최대 입출력전달비로 정의되는 등방성 입출 력전달비가 제시되어 활용되고 있다^[3,17,20].

한편, 병렬 메커니즘의 특이형상이 작업공간내에 존 재하는 경우 실시간 구동시 여유구동을 활용하여 특이 형상을 회피할 수 있는 다양한 방법이 문헌에 제시되었 으며 최근에는 다양한 방법들에 대한 성능 및 효율성 비교에 관한 연구가 수행되었다^[21].

회전관절은 미끄럼 관절에 비하여 마찰력이 적기 때 문에 최소 마찰력이 요구되는 작업에 적용하기 위해 회 전관절만을 사용하는 다양한 형태의 로봇이나 햅틱기기 가 개발되었다^{[3,9,14-17,22-25]}. 그러나, 이들 회전관절만을 사용하는 대부분의 병렬 메커니즘은 정위치 해석해가 존재하지 않으며 따라서 병렬 특이형상 부근에서 수치 해석해는 발산하는 경향을 나타내므로 메커니즘의 성능 이 심각하게 저하되는 경향이 있다.

최근 정위치 해석해를 가지며 무한 회전을 가지는 평 면형 3자유도 병렬 로봇이 제시되어 그 활용 가능성을 보였으며^[24] 햅틱기기로서의 활용 가능성을 검증하기 위 한 목적으로 정위치 해석 및 기구학 해석이 수행되었다^[26,27]. 또한, 하나의 여유구동을 활용하는 위와 동일한 구조에 대한 기구학 특성, 최대 하중, 특이형상 회피 등과 같은 성능을 개선하기 위한 연구와 더불어 시작품이 제작되 었으며 가상벽의 구현을 통한 활용성 및 우수성에 대한 예비실험이 수행되었다.^[26,27] 이와 더불어 엑츄에이터의 최대/최소 토크 한도를 피할 수 있는 여유구동 기법이 제시되었으며 제작된 시작품을 통한 검증 실험이 수행 되었다^[6].

이러한 연구에 이어 본 연구에서는 동일한 평면형 3자 유도 병렬 메커니즘^[6,26,27]에 다수의 여유구동 관절이 장 착되었을 경우의 특이형상 분석, 기구학 등방성 특성, 그 리고 입출력 전달 특성에 대한 분석을 통하여 햅틱기기 로서의 우수성 및 높은 활용 가능성을 확인하고자 한다.

본 논문은 다음과 같이 구성된다. 2장에서는 다수의 여유구동 관절을 가지는 평면형 3자유도 병렬 메커니즘 의 구조 및 기구학 해석에 관한 내용이 요약 기술되며 3장에서는 다양한 수의 여유 구동 관절을 가지는 병렬 메커니즘의 특이형상 분석, 기구학 등방성 특성 분석, 입출력 전달 특성에 대한 분석이 기술된다. 끝으로 결론 을 맺는다.

2. 메커니즘 구조 및 기구학 모델

이 장에서는 먼저 메커니즘 구조에 대해 요약 소개한 다. 그리고 스크류 이론을 활용한 여유구동을 가지는 메 커니즘의 기구학 모델에 대해 요약 기술한다.

2.1. 메커니즘 구조

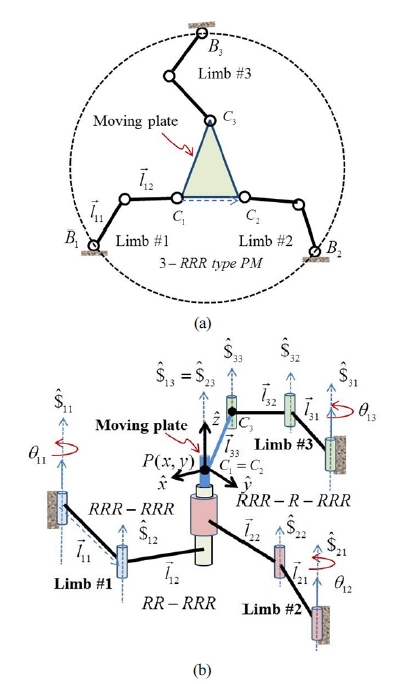
Fig. 1(a)와 Fig. 1(b)는 각각 일반적인 평면형 3자유도 병렬 메커니즘과 정위치 해석해를 가지는 평면형 3자유 도 병렬 메커니즘의 구조를 나타낸다. 사실, Fig. 1(b)의 구조는 Fig. 1(a)의 구조에서 첫 번째 부속체인의 세 번째 관절 축과 세 번째 부속체인의 세 번째 관절 축이 일치하 는 경우에 해당된다(즉, C₁ = C₂). Fig. 1(b)의 병렬 메커 니즘은 기저판, 운동판(moving plate), 그리고 세 개의 회전관절로 이루어진 세 개의 직렬형 부속체인으로 이 루어진다. Fig. 2에서 빨간 원은 병렬 메커니즘을 구동하 는 세 개의 관절을 나타내며 녹색 점선 원은 여유구동 관절로 선택될 수 있는 관절을 나타낸다. 각 부속체인의 두 번째 회전관절이 우선적으로 여유구동 관절로 설정 된 이유는 지면에 고정된 모터로부터 벨트-풀리 전동장 치를 통하여 두 번째 회전관절까지의 구동력 전달이 가 능하여 모터로 인한 관성효과를 최소화할 수 있기 때문 이다. 구체적으로 Fig. 2(a)의 경우에서와 같이 하나의 여유구동 관절이 추가되는 경우 세 번째 부속체인의 두 번째 회전관절이 여유구동 관절로 선정되었으며 Fig. 2(b)의 경우에서와 같이 세 개의 여유구동 관절이 추가 되는 경우 각 부속체인의 두 번째 회전관절이 모두 여유 구동 관절로 선정되었다.

Fig. 1

The planar 3-DOF parallel mechanisms: (a) a typical 3-DOF PM and (b) a modified 3-DOF PM

Fig. 2

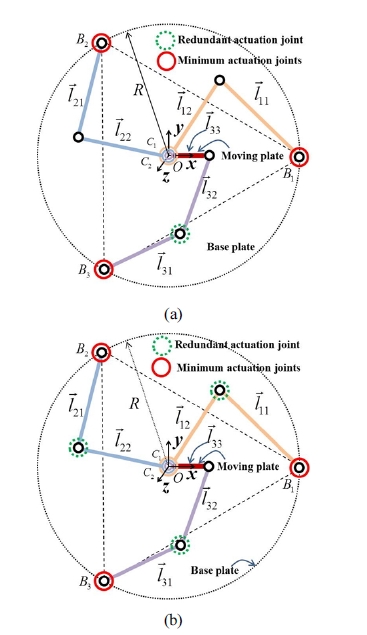
Locations of redundantly actuated joints: (a) one redundant actuation joint and (b) three redundant actuation joints

메커니즘의 기준 좌표계 $(x^b, y^b, z^b)$ 는 하판의 중앙에 위치하며 출력 좌표계 $(x^t, y^t, z^t)$ 는 점 C₁ = C₂ 에 위치한 다. 메커니즘의 출력벡터는 x - y 출력 위치와 회전각 (x_t, y_t, ψ_t) 로 정의되며 여기서 ψ_t 은 EQ 축에 대한 회 전으로 $x^b$ 축으로부터 $x^t$ 까지의 사이 각을 나타낸다. 벡 터 $x^t$ 는 벡터 $l → 33$ 와 동일한 방향이다. 일반적으로 벡터 $l → i j$ 는 $l → i j = l i j l^i j$ 으로 표기되며 여기서 l_ij 는 i 번째 부속체 인의 j 번째 링크의 길이를, $l^i j$ 는 벡터 $l → i j$ 뱡향의 단위 벡터를 나타낸다. θ_ij 는 i 번째 부속 체인의 j 번째 관절의 회전각을 나타낸다. 모든 세 개의 부속체인의 첫 번째 관절 은 각각 하판의 중앙에 위치하며 반경 R 를 가지는 원상에 균일한 오프셋 각 γ_bi (0°, 120°, 240°)의 위치에 설치된다.

2.2. 위치 해석

메커니즘의 역위치 해석은 메커니즘의 출력 위치가 주어졌을 때 입력 관절 변위 값을 구하는 작업이다. 편의 상, 위치 해석에 있어 메커니즘의 입력 관절은 각 부속 체인의 첫 번째 회전 관절로 가정한다. 메커니즘의 각 부속 체인은 모두 직렬 구조이므로 각 부속 체인의 끝 단에 해당되는 메커니즘의 출력 위치가 주어졌을 때 각 부속 체인의 입력 회전 관절 변위 값을 구하는 역위치 해석해는 쉽게 구할 수 있으므로 생략한다^[19].

정위치 해석은 입력 관절 변위 값이 주어졌을 때 출력 위치를 구하는 작업으로 다음과 같은 과정에 따라 수행 될 수 있다. 특히, Fig. 1(b)에 보인 바와 같이 메커니즘의 첫 번째 부속 체인의 세 번째 회전 관절 축과 두 번째 부속 체인의 세 번째 회전 관절 축이 일치한다. 따라서, 축의 위치를 나타내는 점 C₁ (또는 C₂ )의 좌표를 구하기 위해서는 이 들 두 회전 축을 하나의 축으로 간주하여 첫 번째 부속 체인과 두 번째 부속 체인으로 구성되는 5절 기구 폐 체인을 해석함으로써 수행될 수 있다 ^[11,13] . 일단, 점 C₁ 의 좌표 값이 결정되면 C₁ 의 회전 관절을 포함한 세 번째 부속 체인은 4절 기구로써 세 번째 부속 체인의 입력 회전 관절 값이 주어졌을 때 메커니즘 출력 링크의 회전각에 대한 해석해를 구할 수 있다. 이러한 상세한 위치해석 과정은 지면상 생략한다 ^[18,25] .

2.3. 일차 기구학 모델

메커니즘의 일차 기구학 모델은 스크류 이론 (부록 참 조)을 활용하여 유도될 수 있으며^[6,9,27] 다음과 같이 요약 된다. Fig. 2의 평면형 병렬 메커니즘의 각 부속 체인은 동일한 출력 속도를 가지도록 구속되어 있으므로 메커 니즘의 출력 속도 벡터 $(u ˙ = (v x v y ω z) T)$ 와 각 부속 체인의 입력 관절 속도 벡터 $(θ ˙ i = (θ ˙ i1 θ ˙ i2 θ ˙ i3) T, (i = 1, 2, 3))$ 와의 관계식은 다음과 같이 표현된다:

u ˙ = [$^11 $^12] θ ˙ 1 = [$^21 $^22] θ ˙ 2 = [$^31 $^32 $^33] θ ˙ 3 .

(1)

여기서 각 부속 체인의 관절 스크류는 메커니즘의 출력 점 C₁ = C₂ 에 위치한 기준좌표계에 대해 다음과 같이 표현된다:

$^i 1 = (z^(− l → i 1 − l → i 2) × z^) T, $^i 2 = (z^− l → i 2 × z^) T, $^i 3 = (z^0_) T, (i = 1, 2),

(2)

$^31 = (z^(− l → 33 − l → 32 − l → 31) × z^) T, $^32 = (z^(− l → 33 − l → 32) × z^) T, $^33 = (z^− l → 33 × z^) T .

(3)

편의상, 본 논문에서는 위 식에서와 같이 평면형 메커 니즘의 모든 관절 스크류는 3차원 공간에 해당되는 여섯 개의 요소를 가지는 일반적인 형태로 표기되었다. 하지 만, 본 논문에 표기된 모든 트위스트와 렌치는 평면형 공간에서의 운동을 나타내므로 여섯 개의 요소 중에서 평면형 공간 변수에 해당되는 첫 번째, 두 번째, 그리고 여섯 번째 요소만을 취하면 된다:

한편, i 번째 부속 체인내 임의의 구동 관절에 의해 메 커니즘의 출력판에 가해지는 구동 렌치(actuation wrench)는 동일한 부속체인에서 해당 구동 관절을 제외한 나머지 모든 관절에 대한 역수 스크류를 구함으로써 얻어진다. 따라서, 각 체인의 첫 번째와 두 번째 구동 관절에 의해 출력판에 가해지는 구동 렌치는 다음과 같이 구해진다:

$^i 1 r = (l^i 2 0_), $^i 2 r = (l^i 12 0_), (i = 1, 2), $^31 r = (l^32 − l → 33 × l^32), $^32 r = (l^312 − l → 33 × l^312) .

(4)

위 식에서 $l → i12 = l → i1 + l → i2$ 이며 $l^i 12$ 는 $l^i 12$ 각각 해당 방향 의 단위 벡터를 나타낸다.

여유 구동 병렬 메커니즘의 속도 관계식은 (1)의 각 부속 체인 관계식에 (4)에 표현된 각 역수 스크류 (구동 렌치)의 수직 곱 오퍼레이터를 적용한 후 이를 하나의 행렬식으로 정리하면 다음과 같은 형태의 관계식이 얻 어진다^[7]:

[A] u ˙ = [B] θ ˙ a,

(5)

여기서 행렬 A의 각 행 벡터는 구동 렌치를 나타내며 행렬 B 의 비 대각 성분은 구동 렌치와 역수 관계를 가지 므로 모두 영으로 나타난다. 한편, 행렬 B 의 대각 성분 은 각 구동 관절 트위스트와 해당 역수 스크류와의 수직 곱 오퍼레이터를 적용함으로써 얻어진다.

Fig. 2(b)와 같이 각 부속 체인의 첫 번째와 두 번째 관절을 모두 구동하는 $θ ˙ a = (θ ˙ 11 θ ˙ 12 θ ˙ 21 θ ˙ 22 θ ˙ 31 θ ˙ 32) T$ 의 경 우 (5)에서의 행렬 A와 B 는 각각 다음과 같이 얻어진다:

[A] = [$ 11 r T $ 12 r T $ 21 r T $ 22 r T $ 31 r T $ 32 r T] T,

(6)

[B] = [$ 11 r ∘ $ 11 00000 0 $ 12 r ∘ $ 12 0000 00 $ 21 r ∘ $ 21 000 000 $ 22 r ∘ $ 22 00 0000 $ 31 r ∘ $ 31 0 00000 $ 32 r ∘ $ 32]

(7)

여기서 행렬 B 의 대각 성분은 각각 다음과 같이 표현 된다:

$ i 1 r ∘ $ i 1 = l → i 1 ⋅ l^i 2 × z^, $ i 2 r ∘ $ i 2 = l → i 2 ⋅ l^i 12 × z^, (i = 1, 2), $ 31 r ∘ $ 31 = (l → 31 − l → 33) ⋅ l^32 × z^, $ 32 r ∘ $ 32 = l → 32 ⋅ l^312 × z^.

(8)

(5)~(7)에서 원하는 여유 구동 관절들에 대한 식 만을 취함으로써 다양한 위치 및 다수의 여유 구동 메커니즘 에 대한 일차 기구학 관계식을 얻을 수 있다.

(5)의 행렬 B 의 역행렬이 존재하는 경우 메커니즘의 역속도 관계식은 다음과 같이 얻어지며

θ ˙ a = J − 1 u ˙,

(9)

여기서

J − 1 = [B] − 1 [A] .

(10)

메커니즘의 입력 토크(τ)와 출력(f)과의 힘/토크 관 계식은 가상일의 정리로부터 다음과 같이 얻어진다:

f = J − T τ .

(11)

편의상, 지금부터 J^-T 를 나타내기 위해 J_f 가 사용된다 (즉, J^-T =J_f ).

3. 여유 구동 관절수에 따른 기구학 특성 분석

본 장에서는 메커니즘의 병렬 특이 형상 분석, 기구학 등방성 특성, 그리고 입출력 전달 특성이 차례로 기술된다.

3.1. 병렬 특이 형상 분석

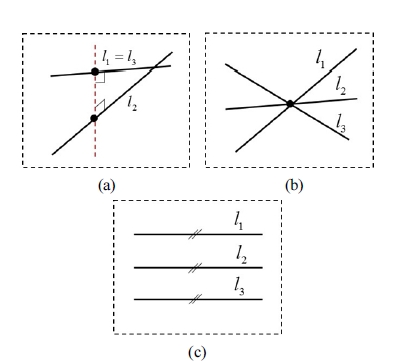
메커니즘의 작업공간내의 병렬 특이 형상을 분석하기 위하여 Grassmann Line Geometry(GLG) 기법이 사용되 었다^[9,10]. 본 연구에서 분석하려는 평면형 3자유도 병렬 메커니즘의 운동판에 전달되는 구동 렌치는 모두 영-피 치(zero-pitch) 렌치로서 간단히 선으로 표기될 수 있으 며 따라서 선의 독립성을 분석함으로써 병렬 특이 형상 을 규명할 수 있다. Fig. 3은 타입 2 특이 형상을 나타낸 다^[9,10]. 메커니즘의 병렬 특이 형상 가운데 하나는 Fig. 3(a)와 같이 모든 구동 렌치가 서로 평행하지도 않고 서 로 만나지 않는 두 개의 선중의 하나와 일치하는 경우에 해당된다. Fig. 3(b)는 모든 구동 렌치가 하나의 공통 교 차점을 가지는 특이 형상을 나타내며 Fig. 3(c)는 모든 구동 렌치가 평행인 특이 형상을 나타낸다.

Fig. 3

Three conditions for Type 2 singularity[9,10]

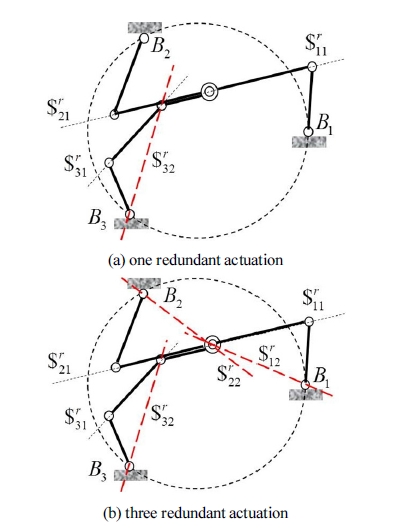
Fig. 4(a)와 Fig. 4(b)는 각각 하나의 여유 구동 관절과 세 개의 여유 구동 관절을 가지는 경우에 대한 구동 렌치 를 나타낸다. 검은 점선은 각 부속 체인의 첫 번째 구동 관절에 의한 구동 렌치를 그리고 굵은 적색 점선은 여유 구동 관절에 해당하는 구동 렌치를 나타낸다. 특히, Fig. 4(a) 는 모든 네 개의 구동 렌치가 하나의 공통 교차점을 가지는 형상을 나타내며 따라서 하나의 여유관절을 가 지는 메커니즘의 경우 적어도 하나 이상의 병렬 특이 형상이 작업공간내에 존재함을 확인할 수 있다. Fig. 4(b) 에서 볼 수 있는 바와 같이 네 개의 구동 렌치의 경우 존재하는 Fig. 4(a)의 특이 형상은 추가된 구동 렌치를 활용함으로써 회피할 수 있음을 알 수 있다. 이로부터 두 개 이상의 여유 구동 관절을 활용하는 경우 본 연구에 서 분석하고자 하는 평면형 3자유도 메커니즘의 병렬 특이 형상은 피할 수 있음을 알 수 있다.

Fig. 4

Removal of parallel singularity via redundant actuation

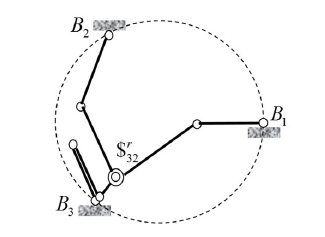
특히, Fig. 5는 메커니즘의 세 번째 부속 체인의 첫 번째와 두 번째 링크가 완전히 겹쳤을 때의 직렬 특이 형상을 나타낸다. 이러한 직렬 특이 형상은 Fig. 6, Fig. 7, 그리고 Fig. 8에서 출력 회전각 y = 270o 일 때의 작업 공간 왼쪽 아래 부분에 있는 흰 원으로 표기된 부분에 해당한다. 특히, 이러한 직렬 특이 형상은 병렬 특이 형 상과는 달리 여유 구동을 통하여 피할 수 없는 특이 형상 이 아니다.

Fig. 5

A serial singularity configuration

Fig. 6

Contour plots of the kinematic isotropy index

Fig. 7

Contour plots of maximum input-to-output force/torque transmission ratio

Fig. 8

Desired motion trajectory and output force

3.2. 기구학 등방성 특성 분석

기구학 등방성 지수(σ_I)는 메커니즘의 등방성 특성을 측정하기 위하여 사용되며 다음과 같이 정의된다:

σ I = σ min σ max

(12)

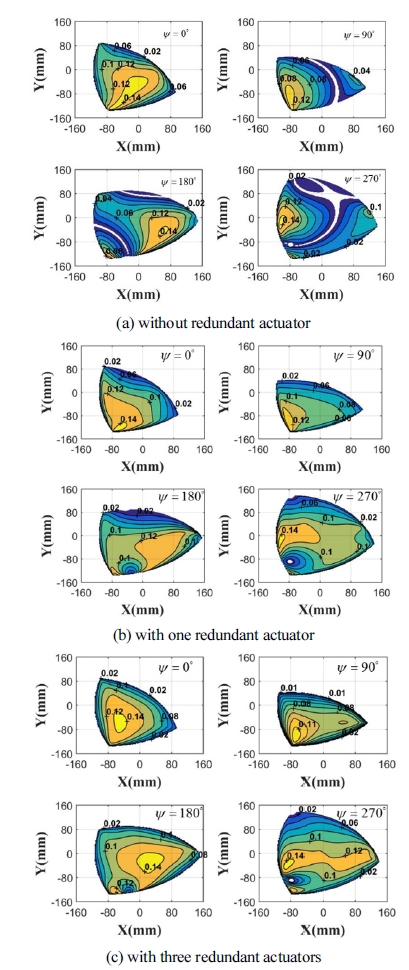
여기서 σ_min 과 σ_max 은 각각 (10)에서 얻어진 역자코비 안 (J^-1)의 최소 특이값과 최대 특이값을 나타낸다. 기 구학 등방성 지수는 정의된 바와 같이 0에서 1사이의 값을 가지며 값이 클수록 우수한 등방성 특성을 나타내 게 된다. Fig. 6(a), Fig. 6(b), 그리고 Fig. 6(c)는 각각 메커니즘이 여유 구동 관절이 없거나, 하나, 또는 세 개 있을 경우에 대해 출력 회전각(ψ)이 각각 0°, 90°, 180° 180 , o and 270°일 때 전체 작업공간내에서의 기구학 등 방성 등고선도를 나타낸다. Fig. 6(a)에서 작업공간내 흰 영역은 기구학 등방성 지수 값이 σ_I=0.01 이하인 병렬 특이 형상의 부근을 나타낸다. 여유 구동이 없는 메커니 즘의 특이 형상은 Fig. 6(a)에서 흰색으로 표현된 영역의 중앙 부근을 지나는 선 또는 점으로써 여유 구동의 존재 여부에 따라 메커니즘 작업공간의 크기는 거의 변하지 않는다. 하지만, Fig 6(a)에 나타난 흰색으로 표현된 특이 형상 부근의 영역은 기구학 특성이 매우 나쁜 영역으로 Fig. 6(b)와 Fig. 6(c)에서와 같이 하나 이상의 여유 구동 을 활용하는 경우 유용한 작업공간의 크기가 증가할 뿐 아니라 작업공간의 중앙부분에 특이 형상이 없기 때문 에 작업공간의 유용성이 크게 개선됨을 알 수 있다. 또 한, Fig. 6(b)와 Fig. 6(c)의 경우 Fig. 6(a)와의 비교할 때, 더 많은 여유 구동 관절이 추가됨에 따라 작업공간 전반에 걸쳐 기구학 등방성 특성이 보다 균일하고 우수 한 영역이 더 많이 확보된다는 사실을 확인할 수 있다.

3.3. 입출력 전달 특성 분석

여유 구동 관절 수에 따른 메커니즘의 성능 비교를 위하여 입출력 힘/토크 전달 특성 분석이 조사하였다. (11)로부터 입출력 전달비의 범위는 다음과 같이 얻어질 수 있다:

σ min ≤ | f | | τ | = τ T J T f J f τ τ T τ ≤ σ max,

(13)

여기서 σ_min 과 σ_max 는 각각 Hermitian 행렬 $J f T J f$ 의 최 소 특이값과 최대 특이값을 나타낸다.

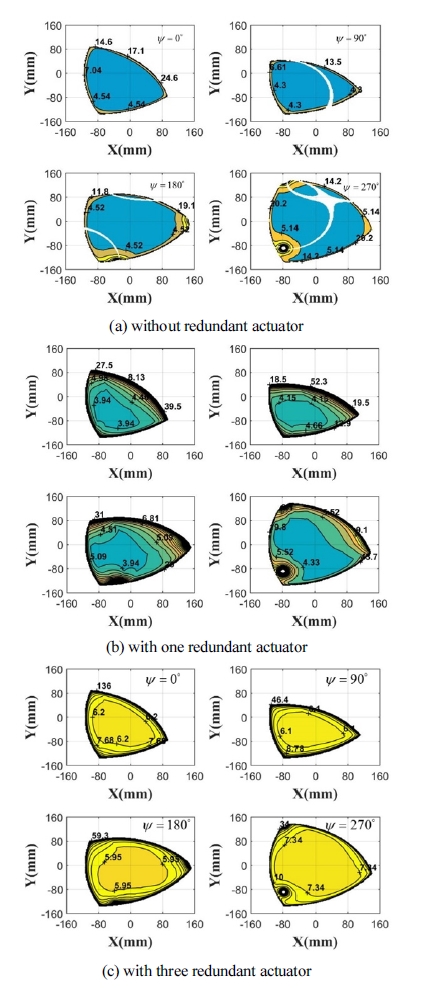
Fig. 7(a), Fig. 7(b), 그리고 Fig. 7(c)는 메커니즘이 여 유구동 관절이 없거나, 하나 또는 세 개의 여유 구동 관 절이 있는 각각의 경우에 대해 출력 회전각(ψ)이 각각 0°, 90°, 180°그리고 270°일 때의 (13)에 정의된 최대 입 출력 힘/토크 전달비 등고선도를 나타낸다. Fig. 7에서도 Fig. 6에서 이미 언급한 바와 같이 병렬 메커니즘의 작업 공간내 흰 부분은 병렬 특이 형상의 부근을 나타낸다. Fig. 7로부터 여유 구동 관절 수가 늘어감에 따라 작업공 간내 최대 입출력 전달비 값이 증가되며 보다 균일한 전달비 특성을 가지는 영역이 확대됨을 확인할 수 있다. 이러한 결과는 여유 구동 관절의 수가 증가됨에 따라 더 큰 값의 구동 렌치가 운동판에 가해지기 때문이라는 것을 쉽게 알 수 있다.

3.4. 여유 구동수에 따른 관절토크 모의실험 비교 분석

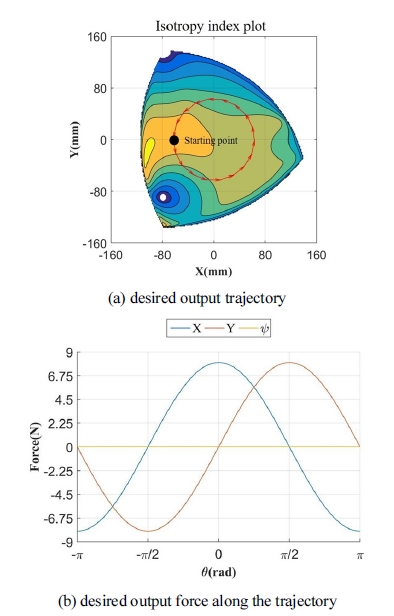
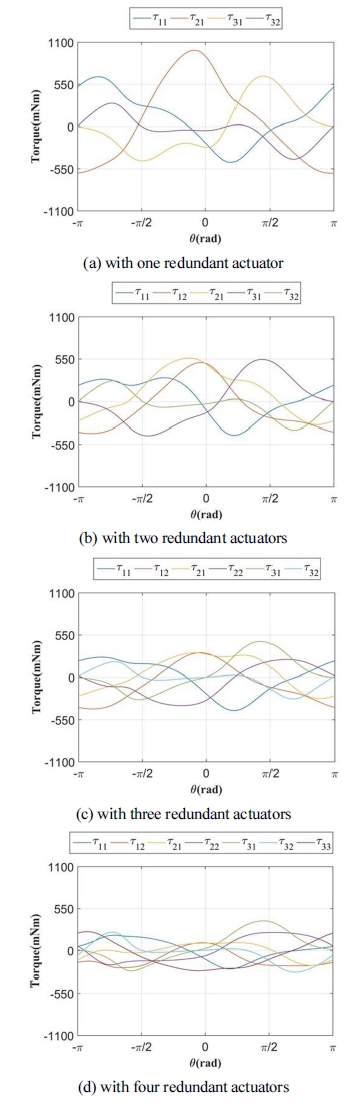
Fig. 8(a)와 같이 원점을 중심으로 반경이 60 mm인 원을 따라 Fig. 8(b)와 같은 출력을 생성하고자 할 때 여유 구동수에 따라 관절토크가 어떻게 분포되는 가를 확인하기 위해 모의실험을 수행하였다. 편의상 여유구 동에 대한 해로서는 관절 토크 최소 놈(joint torque minimum norm : $‖ τ ‖ 2$ ) 해를 활용하였다. Fig. 9(a) ~ Fig. 9(c)는 메커니즘이 지정된 궤적을 따라 이동하되 여유구 동이 하나, 둘, 그리고 셋인 각각의 경우에 대하여 얻어 진 관절토크를 나타낸다. 그리고 Fig. 10(a)는 여유구동 의 수가 다른 각 경우에 대한 관절 토크 최소 놈( $‖ τ ‖ 2$ )을 나타내며 Fig. 10(b)는 Fig. 9(a) - Fig. 9(c) 각각의 경우에 서 얻어진 관절 토크 해에 대한 최대 절대 관절토크 ( ¥ t )값을 나타낸다.

Fig. 9

Joint torques of the PM along the trajectory

Fig. 10

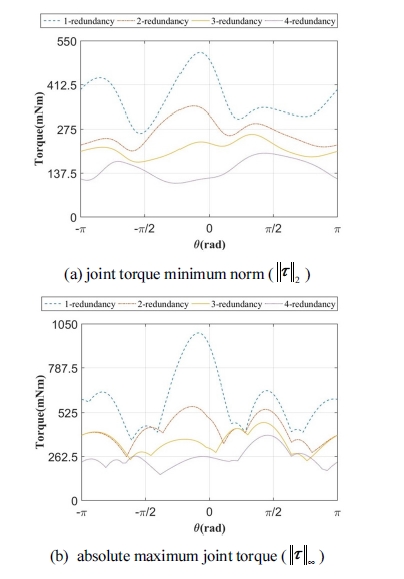
Joint torque minimum norm and absolute maximum joint torque of the PM having different number of actuator redundancy along the trajectory

Fig. 10(a)에서 확인할 수 있는 바와 같이 여유구동수 가 늘어날수록 관절토크 최소 놈의 크기가 현격히 작아 지는 것을 확인할 수 있다. 이러한 결과는 여유구동 수를 늘림으로써 입력관절에서의 에너지를 최소화 할 수 있 음을 나타낸다. 한편, Fig. 10(b)에서도 Fig. 10(a)와 유사 하게 여유구동 수가 늘어날수록 최대 절대 관절 토크의 크기가 작아지는 경향을 확인할 수 있다. 이러한 결과는 최대/최소 관절토크의 제한을 가능한 회피할 수 있도록 Fig. 9에서 확인할 수 있는 바와 같이 모든 관절토크가 균등하게 분배됨을 의미한다. 출력 힘/토크의 측면에서 는 관절토크의 출력토크 제한을 가능한 넘지 않으면서 메커니즘이 발휘할 수 있는 출력 힘/토크의 크기를 증가 시키는 효과를 얻을 수 있음을 의미한다.

4. 결 론

본 논문에서는 햅틱기기로써 제시한 정위치 해석해를 가지며 무한 회전이 가능한 평면형 3자유도 병렬 메커니 즘이 다양한 수의 여유 구동을 가지는 경우 각각에 대한 기구학 특성 분석과 입출력 전달비 특성을 조사하였다. 이러한 해석 결과로부터 본 연구에서 햅틱기기로써 제 시한 여유구동을 가지는 평면평 3자유도 메커니즘은 다 음과 같이 요약되는 매우 우수한 구조 및 기구학 특성을 가지고 있음을 확인하였다: i) 정위치 및 역위치 해석해 가 존재한다, ii) 메커니즘은 출력 링크의 무한 회전이 가능한 구조를 가진다, iii) 회전 관절만을 활용함으로써 최소한의 마찰력을 가진다, iv) 여유 구동을 활용하는 경우 기구학 특성과 힘 전달 특성이 크게 증진될 수 있다, 그리고 v) 두 개 이상의 여유구동을 가지는 경우 작업공 간내에 병렬 특이 형상 회피가 가능한 구조이다.

이러한 결과로부터 본 논문에서 햅틱기기로써 제시한 메커니즘이 여유 구동을 활용하는 경우 보다 우수한 기 구학 특성 및 햅틱기기로서의 우수한 특성을 보유하고 있다는 점을 확인하였으며 기존의 평면형 3자유도 햅틱 기기들 보다 그 응용 가능성 및 우수성이 매우 높다 하겠 다. 한편, 본 연구에서 얻어진 결과들은 본 메커니즘을 여유구동 매니퓰레이터로 활용하는 경우에 유사하게 적 용될 수 있다. 따라서, 향후 과제로 보다 효율적인 여유 구동 기법에 대한 연구 및 슬레이브 메커니즘과의 인터 페이스를 통한 햅틱기기로서의 실시간 활용 성능 분석 에 대한 연구가 추진중에 있다.

부 록^[6,7]

스크류(screw)는 물체의 임의 위치(기준 좌표계 원점) 에서의 속도와 각속도를 나타내는 트위스트(twist)와 힘 과 토크를 나타내는 렌치(wrench)로 나누어진다. 트위스 트는 다음과 같이 정의된다:

$ T = (ω → r → × ω → + v →) = ω (s^r → × s^+ v ω s^) = ω $^T,

(14)

여기서 $s^$ 는 단위 벡터로 트위스트 축을 나타내며 $ω → = ω s^$ 와 EQ $v →$ 스트 축 방향으로의 병진 속도를 나타낸다. $r →$ 은 기준 좌표계로 부터 트위스트 축까지의 위치 벡터이다. 따라서 $r → × ω →$ 는 각속도 $ω →$ 에 의해 발생되는 기준 좌표계 원점의 병진 속도를 의미한다. 그리고 v/ω 는 트위스트 피치 그리고 $$^T$ 는 단위 트위스트라 불리운다.

한편, 렌치는 다음과 같이 정의된다:

$ W = (f → r → × f → + τ →) = f (s^r → × s^+ τ f s^) = f $^W,

(15)

여기서, $f →$ 와 $τ →$ 는 각각 렌치 축 방향으로의 힘과 렌치 축에 대한 토크를 나타낸다. $r →$ 는 기준 좌표계의 원점으 로부터 렌치 축까지의 위치 벡터를 나타내며 따라서, $r → × f →$ 는 힘 $f →$ 에 의해 기준 좌표계의 위치에서 받게 되 는 토크를 나타낸다. 그리고 τ / f 는 렌치 피치 그리고 $$^W$ 는 단위 렌치로 불리운다.

관절 스크류 (트위스트)는 관절 운동에 의해 발생되는 기준 좌표계 원점의 병진 속도와 기준 좌표계의 각속도 로 정의된다. 따라서, 회전 관절 트위스트와 미끄럼 관절 트위스트는 각각 다음과 같이 표현된다:

$ T = (ω → r → × ω →)

(16)

$ T = (0_v →) .

(17)

그리고 기준 좌표계 원점( P )의 병진속도 $(v → p)$ 와 기준 좌 표계의 각속도( $ω →$ )를 나타내는 트위스트는 다음과 같이 표현된다:

$ T p = (ω → v p →) .

(18)

트위스트와 렌치는 각각 속도/각속도와 힘/토크를 나 타내므로 다음과 같이 정의되는 수직 곱(orthogonal product) 오퍼레이터를 통해 이들로 인한 전달 동력(transmission power)를 산출할 수 있다.

$ T ∘ $ W = (ω → r → × ω → + v →) ∘ (f → r → × f → + τ →) = ω → ⋅ (r → × f → + τ →) + (r → × ω → + v →) ⋅ f → .

(19)

특히, 위 수직 곱 오퍼레이터의 결과가 영이 되는 경우 해당 트위스트와 렌치는 서로 역수(reciprocal)라고 불리 우며 이들 간의 상호작용으로부터 동력 전달은 없다는 것을 의미한다.

References

Hollerback, J, Redundancy resolution of manipulators through torque optimization, IEEE Trans. Rob. Autom, (1987), 3(4), p308-316. [https://doi.org/10.1109/JRA.1987.1087111]
Nakamura, Y, Hanafusa, H, Yoshikawa, T, Taskpriority based redundancy control of robot manipulators, Int J. Rob. Res., (1987), 6(2), p3-15. [https://doi.org/10.1177/027836498700600201]
Kock, S, Schumacher, W, A parallel x-y manipulator with actuation redundancy for high-speed and activestiffness applications, IEEE Trans. Int. Conf. Robot. Auto, (1998, May), p2295-2300.
Kim, T. J, Yi, B-J, Suh, I.H, Load distribution algorithms and experimentation for a redundantly actuated, singularity-free 3-DOF parallel haptic device, In Proceedings of the IEEE int'l conference on intelligent robotics and systems, (2004), p2899-2904.
Saglia, J. A, Dai, J. S, Caldwell, D. G, Geometry and Kinematic Analysis of a Redundantly Actuated Parallel Mechanism That Eliminates Singularities and Improves Dexterity, ASME Journal of Mechanical Design, (2008), 130(12), p124501_1-5. [https://doi.org/10.1115/1.2988472]
Woo, S. H, Kim, S. M, Kim, M. G, Yi, B.-J, Kim, W.K, Torque Balancing Algorithm for the Redundantly Actuated Parallel Mechanism, Mechatronics, (2017), 42, p41-51. [https://doi.org/10.1016/j.mechatronics.2017.01.002]
Tsai, L. W, Robot Analysis: The Mechanics of Serial and Parallel Manipulators, Wiley-Interscience, (1999).
Lee, G, Park, S, Lee, D, Park, F. C, Jeong, J. I, Kim, J, Minimizing energy consumption of parallel mechanism via redundant actuation, IEEE/ASME Trans. Mechatron., (2015), 20(6), p2805-2812. [https://doi.org/10.1109/tmech.2015.2401606]
Merlet, J. P, Parallel Robots, Kluwer Academic Publishers, (2000).
Hao, F, McCarthy, J. M, Conditions for line-based singularities in spatial platform manipulators, J. of Robotic Sys., (1988), 15(1), p43-55. [https://doi.org/10.1002/(sici)1097-4563(199812)15:1<43::aid-rob4>3.0.co;2-s]
White, N. L, Grassmann-Cayley algebra and robotics, Journal of Intelligent Robot Systems, (1994), 11, p91-107. [https://doi.org/10.1007/bf01258296]
Ben-Horin, P, Shoham, M, Application of Grassmann-Cayley algebra to geometrical interpretation of parallel robot singularities, International Journal of Robotics Research, (2009), 28(1), p127-141. [https://doi.org/10.1177/0278364908095918]
Shin, K, Yi, B.-J, Kim, W, Parallel singularity-free design with actuation redundancy: A case study of three different types of 3-degree-of-freedom parallel mechanisms with redundant actuation, Proceedings of the Institution of Mechanical Engineers, Part C: J Mechanical Engineering Science, (2014), 228(11), p2018-2035. [https://doi.org/10.1177/0954406213512246]
Yi, B.-J, Kim, S.M, Kwak, H.K, Kim, W.K, Multi-task oriented design of an asymmetric 3T1R type 4-DOF parallel mechanism, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, (2013), 227(10), p2236-2255. [https://doi.org/10.1177/0954406212473726]
Kim, S. M, Yi, B.-J, Kim, W. K, Forward kinematic singularity avoiding design of a sch nflies motion generator by asymmetric attachment of subchains, International Journal of Control, Automation, and Systems, (2013), 11(1), p116-127. [https://doi.org/10.1007/s12555-012-0005-5]
Park, J. H, Kim, S. M, Kim, W. K, Analysis on Kinematic Characteristics of the Revolute joint-based Translational 3-DOF Parallel Mechanisms, Journal of Korea Robotics Society, (2015), 10(2), p119-132. [https://doi.org/10.7746/jkros.2015.10.2.119]
Kim, S. M, Shi, K. S, Yi, B.-J, Kim, W. K, Development of a novel two-limbed parallel mechanism having sch nflies motion, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, (2015), 229(1), p136-154. [https://doi.org/10.1177/0954406214532633]
Oh, H.S, Yi, B.-J, Kim, W.K, Kinematic Characteristic Analysis of a Planar 3-DOF Parallel Mechanism Having Closed-form Position Solution, The 8 th Korea Robotics Society Conference, (2013), p390-391.
Oh, H.S, Kinematic Characteristic Analysis of a Planar 3-DOF Parallel Mechanism Having Closed-form Position Solution, Master's thesis, Korea university, (2013, June).
Lee, J.H, Yi, B.-J, Oh, S.R, , Optimal design and development of a five-bar finger with redundant actuation, Mechatronics, (2001), 11, p27-42. [https://doi.org/10.1016/s0957-4158(99)00089-6]
Kim, S.H, Park, J.H, Singularity Avoidance Algorithms for Controlling Robot Manipulator: A Comparative Study, Journal of Korea Robotics Society, (2017), 12(1), p42-54. [https://doi.org/10.7746/jkros.2017.12.1.042]
Tsai, L.W, Walsh, G. C, Stamper, R. E, Kinematics of a novel three DOF translational platform, Proceedings of the IEEE Int. Conf. Robot. Auto, (1996), p3446-3451.
Wua, J, Wanga, J, You, Z, A comparison study on the dynamics of planar 3-DOF, 4-RRR, 3-RRR and 2-RRR parallel manipulators, Robotics and Computer-Integrated Manufacturing, (2011), 27, p150-156. [https://doi.org/10.1016/j.rcim.2010.07.001]
Arakelian, V, Briot, S, Yatsun, S, Yatsun, A, A new 3-DoF planar parallel manipulator with unlimited rotation capability, 13th World Congress in Mechanism and Machine Science, (2011, June), IMD-123.
Fu, Y, Yang, Y, Pan, B, Wang, S, Dynamic modeling and analysis of a 3-DOF parallel haptic device, Proceedings of 2013 IEEE Conf. on Mechatronics and Automation, Japan, (2013), p110-115.
Jeon, J.I, Oh, H.S, Park, J.H, Kim, W.K, Implementation of the redundantly actuation planar parallel mechanism having closed-form forward position solution, Proceedings of the KSPE Conf, (2013), Fallp313-314.
Jeon, J.I, Redundant Actuation Characteristics Analysis and Practical Redundancy Algorithm of a Planar 3-DOF Parallel Mechanism Having Closed-form Position Solution, Master's thesis, Korea university, (2014, Dec).

전 정 인

2013 고려대학교 제어계측공학과(공학사)

2015 고려대학교 대학원 제어계측공학과(공 학석사)

2015~현재 주) 삼영기계 기술연구소 선임연 구원

관심분야: 로봇 메커니즘 설계, 기구학 모델링, 햅틱기기, 여유구동 로봇, 시스템 자동화

오 현 석

2011 고려대학교 전자 및정보공학부(공학사)

2013 고려대학교 대학원 제어계측공학과(공 학석사)

2014~현재 두림 야스카와 기술 연구소 주임 연구원

관심분야: 로봇 메커니즘 설계, 기구학 모델링, 햅틱기기., 마이크로 프로세서 응용

우 상 훈

2014 고려대학교 제어계측공학과(공학사)

2017 고려대학교 대학원 제어계측공학과 (공학석사)

2017~현재 ABB Ltd., robotics advanced engineering team, project engineer

관심분야: 로봇 메커니즘 설계, 기구학 모델링, 햅틱기기, 여유구동 로 봇 기전융합시스템, 로봇 응용 시스템

김 성 목

2011 고려대학교 대학원 제어계측공학과 (공학석사)

2017 고려대학교 대학원 제어계측공학과 (공학박사)

2017~현재 주) 고영테크놀러지 Advanced Medical Instrument team 과장

관심분야: 병렬 메커니즘 설계, 기구학 모델링, 모바일 로봇, 의료 로봇

김 민 건

1986 일본 Keoi대학교 기계공학과(공학박사)

1986~현재 강원대학교 기계메카트로닉스 공학부 교수

관심분야: 파괴, 바이오 메커니즘 설계 분석 및 응용

김 희 국

1990 텍사스 주립대학교 기계공학과(공학 박사)

1990 텍사스 주립대학교 기계공학과 Post Doc.

1991~현재 고려대학교 제어계측 공학과 교수

관심분야: 병렬 메커니즘 설계, 기구학 및 동역학 모델링, 모바일 로봇, 여유구동 로봇, 햅틱기기, 의료 로봇