병렬로봇의 설계 공차가 궤적 정밀도에 미치는 영향 분석

1. 서 론

일반적인 직렬기구의 오차는 각 관절들이 직렬로 연결되 므로 공차에 의한 오차 또한 누적되는 경향을 가지는 것이 자명하다. 그러나 병렬기구는 각 관절이 병렬로 연결되므로 오차가 누적되지 않고 평활화되는 경향이 있어 단편적으로 예측하기 어렵다. 이러한 문제를 분석하기 위한 관련된 연 구로 델타로봇 오차 모델링에 관한 연구^[1]가 있다. 연구^[1]에 서 로봇의 오차를 계통오차와 우연오차 요인으로 크게 두가 지 종류로 구분하고 있다. 계통오차는 주로 제작시 발생하 는 가공 오차, 조립오차 등과 같은 기구학적으로 모델링이 가능한 오차를 말하고, 우연오차는 주로 작업시 발생하는 외란, 변형, 백래시 등과 같이 모델링이 불가능한 오차를 말한다.

본 저자들은 선행연구를 통해 문헌^[2]에서 우연오차가 병 렬로봇의 위치정밀도에 미치는 영향은 배제하고 계통오차 에 의해 발생되는 기구적 오차를 분석한바 있다. 이를 통해 작업공간상의 특정 개수의 점들에서의 오차를 분석하는 알 고리즘을 개발하고 적용하여 그 경향성 분석을 진행하여 최종 위치정밀도에 영향을 민감하게 주는 설계 파라미터와 둔감한 파라미터를 구분할 수 있었다.

본 논문에서는 각 포인트에서의 에러를 분석하는 연구를 더욱 발전시켜 목표궤적을 추종하는 경우에 경로를 따라 발생하는 실제 에러의 경향성을 면밀히 분석함으로써 설계 자가 설계단계에서 각각의 설계 파라미터가 로봇 말단의 오차에 어떤 영향을 미치는지에 관한 더욱 풍부한 정보를 제공하고자 한다. 설계자는 자신이 설계한 로봇이 주로 사 용되는 모션(궤적)에서 어떠한 경향성을 가지고 에러를 발 생시키는지를 한눈에 파악할 수 있으므로 설계단계에서 기 구적 부정확성이 최종 제작되는 병렬로봇의 궤적정밀도에 어떠한 영향을 미치는지를 이해하고 대책을 마련하는데 효 과적으로 활용될 수 있을 것이다.

2. 3자유도 병렬로봇의 기구학 및 설계 파라미터 정의

최근에 점차 병렬로봇이 고속화, 정밀화 되고 있으며 이 와 같은 이유로 델타로봇^[3,4,5]에 대한 수요가 급속히 증가하 고 있다. 따라서 본 연구에서는 델타로봇을 대상으로 궤적 정밀도를 분석하였다.

직렬로봇의 경우 정기구학(Forward Kinematics)이 쉽고 역기구학(Inverse Kinematics)이 어려우나 병렬로봇인 델 타로봇^[5]의 경우 쌍대성 원리^[6]에 의해 역기구학(Inverse kinematics)은 쉬우나 정기구학(Forward kinematics)은 어 렵다^[8,9]. 따라서 정기구학은 수치해석적인 방법을 통해 해 를 구한다. 역방향기구학은 끝단의 위치(Pc)가 주어질 때, 능동 조인트, 즉, 모터의 회전각을 계산하는 것이고 정기구 학은 반대로 모터의 회전각이 주어질 때, 끝단의 위치를 계산하는 것이다^[7].

기구적 요인에 의해서 발생하는 궤적에러를 분석하기 위 하여 주요 설계 파라미터를 정의하는 것이 필요한데, 본 논문에서는 문헌^[2]에서 정의된 좌표계(Fig. 1), 델타 로봇 암의 기구학적 단순화 모델(Fig. 2), 그리고 해석파라미터 (Fig. 3)를 동일하게 적용한다. 로봇의 베이스 플랫폼의 중 앙에 원점을 가지는 좌표계 {b}를, Traveling plate 중앙에 좌표계 {p}를 정의한다. 좌표계 {b}의 축 방향에 첫 번째 암이 설치되고 반 시계 방향 120° 간격으로 각각 두 번째, 세 번째 암이 설치된다. Fig. 2의 단순화 모델을 통해서 각 암의 운동 구속식을 식 (1)과 같이 표현할 수 있고, 이를 통해 로봇 끝단의 위치를 구할 수 있다.

Fig. 1

Definition of Coordinates of parallel kinematic robot

Fig. 2

Simple model of the parallel kinematic robot of Fig. 1

Fig. 3

Definition of kinematic parameter for analysis

본 연구에서 해석하고자 하는 설계 파라미터는 Fig. 3과 같이 정의 된다. 또한 본 연구에서는 중앙 회전축에 의한 회전 각도는 모터에 의한 직접적인 회전으로 간주하여 오차 가 발생하지 않는 것으로 무시하고 해석한다.

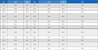
Table 1은 Fig. 3에 표시된 해석 파라미터(설계의 기구적 변수)의 명칭과 기호 그리고 대응되는 공차의 명칭을 요약 하고 있다. 이들 공차의 변동에 의하여 델타로봇 말단이 원형궤적을 그릴 때 발생하는 오차를 계산함으로써 해석 파라미터가 궤적오차에 미치는 영향을 분석한다.

Table 1

Definition of design parameter

Fig. 4

Definition of a circle trajectory for the analysis of trajectory tracking errors

3. 궤적추종오차 해석 방법 정의

본 연구에서는 궤적오차의 분석을 위하여 측정한 반경을 가지는 원을 그렸을 때 주어진 공차에 의하여 나타나는 궤 적에러를 분석하였다. 이를 위하여 아래의 단계를 거치는 해석 절차를 구현하였다.

• 1) 원형 궤적의 원점 정의: P1(0,0,-250)을 원점으로 하는 반지름 200인 원을 5도 간격으로 72등분하는 위치를 $$ {\overrightarrow{P}}_c$$로 정의 한다.
• 2) 공차의 정의 : Fig. 3과 Table 1에 정의된 바와 같이 공차 를 정의한다(d는 하한공차, u는 상한공차를 의미한다).
• 3) 모든 파라미터에 공차가 없을 경우에 해석위치( $$ {\overrightarrow{P}}_c$$)에 대한 능동 조인트 각도 $$ {\overrightarrow{\theta }}_n$$를 역기구학 해석(Inv_Kin) 을 통해 구한다( $$ {\overrightarrow{P}}_{ck}$$ 위치에서 능동조인트의 각도 $$ {\overrightarrow{\theta }}_k$$).
• 4) 기구학 파라미터에 공차가 있을 경우의 로봇의 말단 의 위치를 구한다.
• 5) 기구학 파라미터에 공차가 없을 경우의 로봇의 말단 의 위치와 기구학 파라미터에 상한 공차가 있을 경우 의 로봇의 말단 위치와의 오차의 RMS(Root Mean Square)를 연산한다. 각각의 오차에 대한 에러를 $$ {\overrightarrow{e}}_n^u\left(1\right),{\overrightarrow{e}}_n^u\left(2\right),\hspace{0.17em}\cdots {\overrightarrow{e}}_n^u\left(8\right)$$ 로 표시한다. 여기서
  

  $\[ \begin{array}{l}{\overrightarrow{e}}_n^u\left(1\right)=\left[e_n^u\left(1\right),e_n^u\left(1\right),\cdots ,e_n^u\left(1\right)\right]\\ {\overrightarrow{e}}_n^u\left(2\right)=\left[e_n^u\left(2\right),e_n^u\left(2\right),\cdots ,e_n^u\left(2\right)\right]\\ {\overrightarrow{e}}_n^u\left(3\right)=\left[e_n^u\left(3\right),e_n^u\left(3\right),\cdots ,e_n^u\left(3\right)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\overrightarrow{e}}_n^u\left(8\right)=\left[e_n^u\left(8\right),e_n^u\left(8\right),\cdots ,e_n^u\left(8\right)\right]\end{array} \]$

  
  이다.
  기구학 파라미터에 공차가 없을 경우의 로봇의 말단의 위치와 기구학 파라미터에 하한 공차가 있을 경우의 로봇의 말단 위치와의 오차의 RMS (Root Mean Square)를 연산한다. 각각의 오차에 대한 에러를 로 표시한다. 여기서
  

  $\[ \begin{array}{l}{\overrightarrow{e}}_n^d\left(1\right)=\left[e_n^d\left(1\right),e_n^d\left(1\right),\cdots ,e_n^d\left(1\right)\right]\\ {\overrightarrow{e}}_n^d\left(2\right)=\left[e_n^d\left(2\right),e_n^d\left(2\right),\cdots ,e_n^d\left(2\right)\right]\\ {\overrightarrow{e}}_n^d\left(3\right)=\left[e_n^d\left(3\right),e_n^d\left(3\right),\cdots ,e_n^d\left(3\right)\right]\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}⋮\\ {\overrightarrow{e}}_n^d\left(8\right)=\left[e_n^d\left(8\right),e_n^d\left(8\right),\cdots ,e_n^d\left(8\right)\right]\end{array} \]$

이다.

개발된 오차 해석 알고리즘을 시각화하여 간단히 정리 하면 Fig. 5와 같다. 위첨자 u는 공차의 상한을 d는 하한을 나타낸다. $$ P_{r1},P_{r2},\cdots ,P_{rn}$$ 은 해석을 진행하는 로봇의 말단 위치를 의미하며 θ_n 은 P_rn 에 도달하기 위 해 역기구학을 풀어서 계산된 조인트 각도를 의미한다.

Fig. 5

Flow chart of error analysis of trajectory tracking error

4. 오차 해석 결과 및 분석 순서

3장에서 요약된 해석 절차를 통하여 7종류의 설계 파라미 터의 공차 수준에 의해 발생하는 로봇 말단의 궤적오차를 분석하였다. 우선 이러한 분석을 자동화 하여 수행할 수 있도록 궤적오차 해석 프로그램을 개발하였다. Fig. 6은 개 발된 해석 프로그램의 실행화면을 보여준다. 본 장에서는 해석결과를 시각적으로 보이기 위하여 개발된 프로그램의 결과 화면을 캡처하여 첨부한다.

Fig. 6

The developed program to analyze trajectory tracking error

아래의 결과 분석을 위한 그림들은 설계 공차의 상한과 하한이 적용되었을 때 원형 경로를 추정하는 과정에서 발생 하는 오차로 표현된다. Fig. 7, 9, 11, 13, 15, 17, 19, 21에서 x, y, z축은 각각 수직, 수평방향을 의미하며 x, y 축의 단위 는 mm이다. Fig. 8, 10, 12, 14, 16, 18, 20, 22에서 가로축 은 x축을 기준으로 원형궤적 상에서의 위치를 표시하기 위 한 각도이고, y축은 궤적 상에서의 위치오차를 나타낸다.

Fig. 7

Trajectory simulation with no tolerance of “base joint offset (OB )” (Green), with upper limit tolerance (Red) and with lower limit tolerance (Blue). Unit of x, y and z is millimeter

Fig. 8

Trajectory errors caused by “base joint offset (OB )” (Red: x directional error, Green: y directional error, Blue: z directional error)

Fig. 9

Trajectory simulation with no tolerance of “base joint angle (AS )” (Green), with upper limit tolerance (Red) and with lower limit tolerance (Blue). Unit of x, y and z is millimeter

Fig. 10

Trajectory error caused by “base joint angle (AS )” (Red: x directional error, Green: y directional error, Blue: z directional error)

Fig. 11

Trajectory simulation with no tolerance of “base radius (RB )” (Green), with upper limit tolerance (Red) and with lower limit tolerance (Blue). Unit of x, y and z is millimeter.

Fig. 12

Trajectory error caused by “base radius (RB )” (Red: x directional error, Green: y directional error, Blue: z directional error)

Fig. 13

Trajectory simulation with no tolerance of “platform radius (Rp )” (Green), with upper limit tolerance (Red) and with lower limit tolerance (Blue). Unit of x, y and z is millimeter.

Fig. 14

Trajectory error caused by “platform radius (Rp )” (Red: x directional error, Green: y directional error, Blue: z directional error)

Fig. 15

Trajectory simulation with no tolerance of “motor installation height (HM )” (Green), with upper limit tolerance (Red) and with lower limit tolerance (Blue)

Fig. 16

Trajectory error caused by “motor installation height (HM )” (Red: x directional error, Green: y directional error, Blue: z directional error)

Fig. 17

Trajectory simulation with no tolerance of “arm length (LA )” (Green), with upper limit tolerance (Red) and with lower limit tolerance (Blue). Unit of x, y and z is millimeter

Fig. 18

Trajectory error caused by LA “arm length (LA )” (Red: x directional error, Green: y directional error, Blue: z directional error)

Fig. 19

Trajectory simulation with no tolerance of “leg length (LL )” (Green), with upper limit tolerance (Red) and with lower limit tolerance (Blue). Unit of x, y and z is millimeter.

Fig. 20

Trajectory error caused by “leg length (LL )” (Red: x directional error, Green: y directional error, Blue: z directional error)

Fig. 21

Trajectory simulation with no tolerance of all parameters (Green), with upper or lower tolerance(Blue). Unit of x, y and z is millimeter.

Fig. 22

Trajectory error caused by all parameters (Red: x directional error, Green: y directional error, Blue: z directional error)

5. 결 론

본 논문은 작업공간상의 임의의 포인트에서의 로봇 말단 의 에러를 분석하는 연구를 더욱 발전시켜 목표궤적을 추종 하는 경우에 경로를 따라 발생하는 실제 에러의 경향성을 면밀히 분석함으로써 설계자가 설계단계에서 각각의 설계 파라미터가 로봇 발단의 오차에 어떤 영향을 미치는지에 관한 더욱 풍부한 정보를 제공한다. 설계자는 자신이 설계 한 로봇이 주로 사용되는 모션(궤적)에서 어떠한 경향성을 가지고 에러를 발생시키는지를 한눈에 파악할 수 있으므로 설계단계에서 기구적 부정확성이 최종 제작되는 병렬로봇 의 궤적정밀도에 어떠한 영향을 미치는지를 이해하고 대책 을 마련하는데 효과적으로 활용될 수 있을 것이다.

References

• W.J. Shin and N.G. Cho, “A study on the error compensation of three-DOF translational parallel manipulator,” Transactions of the Korean Society of Machine Tool Engineering, vol.13, no.3, pp.44-52, Jun. 2004.
• C.H. Park, “The effects of design parameters on the mechanical precision of an end effector on a parallel kinematic robot,” Journal of Institute of Control, Robotics and Systems, Vol.22, no.10, pp.847-852, October, 2016 [https://doi.org/10.5302/J.ICROS.2016.16.0169]
• R. Clavel, “Conception d’un robot parallèle rapide à 4 degrés de liberté,” Ph.D. Thesis, EPFL, Lausanne, Switzerland, 1991.
• R. Clavel, “Device for the movement and positioning of an element in space,” US Patent No.4,976,582, Dec. 1990
• J.-P. Merlet, Parallel Robots, Kluwer Academic Publishers, 2000. [https://doi.org/10.1007/978-94-010-9587-7]
• K. Miller, “Modeling of dynamics and model-based control of DELTA direct-drive parallel robot,” Journal of Robotics and Mechatronics, Vol.17, no.4, pp.344-352, 1995. [https://doi.org/10.20965/jrm.1995.p0344]
• S.H. Lee, “Dynamic modeling of a novel ATC mechanism based on 4-bar linkage,” Journal of Institute of Control, Robotics and Systems, vol.22, no.4, pp.307-314, 2016. [https://doi.org/10.5302/J.ICROS.2016.15.0182]
• P. J, “Vibration analysis of planar cable-driver parallel robot configurations,” Journal of Korea Robotics Society, Vol.11, no.2, pp.73-82, 2016. [https://doi.org/10.7746/jkros.2016.11.2.073]
• J.H. Park, “Analysis on Kinematic Characteristics of the Revolute joint-based Translational 3-DOF Parallel Mechanisms,” Journal of Kora Robotics Society, Vol.10, no.2, pp.119-132, 2015. [https://doi.org/10.7746/jkros.2015.10.2.119]