평면형 케이블 구동 병렬로봇의 구조에 따른 진동분석

1. 서 론

케이블 구동 병렬로봇(이하 케이블 로봇)은 전통적인 직렬 로봇과 달리 가볍고 유연한 케이블로 엔드이펙터 와 프레임을 연결하여 케이블을 감고 푸는 방식으로 구 동된다. 따라서 케이블 로봇은 케이블의 가벼운 무게와 길이의 가변성으로 높은 가반하중, 넓은 작업공간, 고속 작동 가능 등의 장점을 갖고 있다. 또한 케이블 로봇은 작업공간과 작업환경에 따라 프레임과 엔드이펙터를 사 용자가 원하는 형태로 구성할 수 있다. 이러한 장점으로 케이블 로봇은 태양광패널 설치, 전파망원경(aperture spherical radio telescope), pick and place 작업 등의 영역 에서 효과적으로 사용될 수 있다^[1-3]. 그러나 케이블의 탄성과 유연성은 케이블의 진동문제를 일으켜 엔드이펙 터 이동 정밀도를 저해하고 작업의 진행에 어려움을 가 져다 줄 수 있다.

케이블 로봇의 진동문제를 해결하기 위해 진동제어와 진동분석에 관한 여러 가지 연구가 진행되어 왔다. 그 중에는 극점배치, 선형이차, 퍼지PID, 반작용 휠 을 사용 하여 진동을 줄이는 연구들과^[4-8] 특정한 응용시스템에 대한 진동분석의 연구가 있었다. 케이블 로봇의 진동은 케이블의 횡 방향 진동과 축 방향 진동으로 나눌 수 있는 데 많은 연구자들이 축 방향의 진동만 고려하여 운동방 정식을 유도해왔다^[9-11]. 케이블 횡 방향 진동이 엔드이펙 터 진동에 대한 영향을 분석하기 위해 Diao와 Ma는 횡 진동과 축 진동을 비교 분석하여 횡 방향 진동의 영향이 충분히 작으므로 무시할 수 있다는 결론을 얻었다^[12]. 최 근에 설치중인 세계 최대 전파망원경 FAST (Five-hundredmeter Aperture Spherical radio Telescope)를 기반으로 Z. Liu 등은 큰 공간에서는 횡 진동도 연구할 필요가 있다는 관점에서 케이블 처짐을 고려하여 파동방정식으 로 횡 진동에 대한 분석을 하였지만^[13] 횡 진동의 영향이 적어 케이블 로봇 구동 시의 자유진동에 대한 분석은 축 방향 진동으로 모델링 하였다^[14]. Tang, Li 등은 Tendon-based 케이블 로봇의 진동분석으로 엔드이펙터 의 이심률과 질량이 어떤 특정한 가진 주파수에서 시스 템을 불안정하게 하는데 중요한 역할을 한다는 결론을 얻었다^[15]. 지금까지의 연구들은 특정한 응용 시스템에 대한 진동분석과 진동제어에 초점을 두었으며 일반적인 케이블 로봇에서의 고유진동수를 고려한 프레임과 엔드 이펙터 형상 및 케이블 연결방식에 대한 설계 방안은 없었다.

본 논문에서는 완전구속 평면형 4케이블 로봇을 기반 으로 로봇 형상 변화에 따른 진동분석을 통해 고유진동 수 측면에서 진동에 강한 케이블 로봇 디자인을 제안하 고자 한다. 케이블 로봇의 구조에는 프레임 형상, 엔드이 펙터 형상과 케이블 연결방식이 포함될 수 있다. 케이블 로봇 형상변화에 대한 진동분석을 하기 위해 프레임과 엔드이펙터의 면적을 고정시키고 가로 세로의 비율을 무차원 파라미터로 정하였다. 케이블은 선형 스프링으 로 모델링 하였고 정상연결, 위아래 교차연결과 좌우 교 차연결에 대해 각각 분석하였다. 분석 결과 일반적인 평 면형 케이블 로봇에서 외란에 강한 로봇구조를 제안할 수 있었다.

2. 기구학과 운동방정식

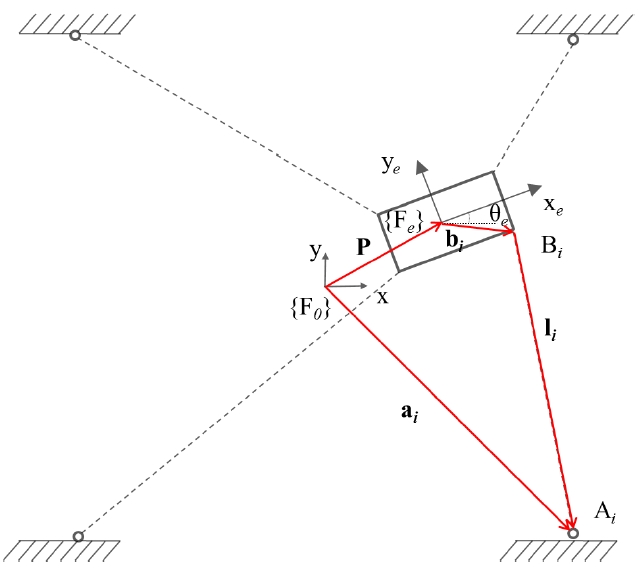
본 연구실에서는 Fig. 1과 같은 구성의 완전구속 (fully-constrained) 평면형 4케이블 로봇을 개발 중에 있 으며, Fig. 2는 본 평면형 케이블 로봇의 도식화된 기구 학을 보여준다. {F0}는 기준 좌표계이고 {Fe}는 엔드이 펙터 좌표계이다. Ai, Bi (i=1, 2, 3, 4)는 각각 프레임과 엔드이펙터에 위치한 고정점이다. ai는 기준 좌표계 {F0}를 기준으로 표현된 Ai 상수 위치벡터이고, bi는 엔 드이펙터 좌표계 {Fe}를 기준으로 표현된 Bi 상수 위치 벡터이며, li는 케이블 길이와 방향을 표시하는 벡터이 다. 위의 관계로 위치벡터 P는 다음과 같이 표시할 수 있다.

Fig. 1

Configuration of a real planar four cable robot

Fig. 2

Kinematic of a fully-constrained planar four cable robot

식 (1)에서 R는 {F0} 기준의 {Fe}의 방향을 표시한 회전행렬이다. 식 (1)을 사용하여 케이블 길이를 식 (2) 와 같이 나타낼 수 있다.

케이블 로봇의 축 방향 진동을 분석하기 위해 케이블 은 선형 스프링으로 모델링하고 2.5 mm 직경인 LIROS D-Pro 01505-0250 Dyneema SK 75 fiber의 강성 120,000 N/m을 선택하였다^[16]. 완전구속 평면형 4케이블 로봇의 운동 방정식은 식 (3)의 라그랑주 방법을 적용하여 얻을 수 있다.

식 (3)에서 위치행렬 q는 [x, y, θ]T이고 운동에너지 T 와 위치에너지 U 는 식 (4), 식 (5)에서 나타내고 있다.

진동 시의 위치행렬 P′와 회전행렬 R′를 식 (7)과 같 이 정의할 수 있다.

여기서 x0, y0, θ0는 엔드이펙터가 진동하기 전 위치와 회전각도이다. 케이블의 길이는 엔드이펙터 자세(x0, y0, θ0)에 따라 달라지고 따라서 식 (6)에 의하여 케이블 강 성 또한 케이블 길이에 의해 달라진다.

라그랑주 방법으로 유도된 방정식은 복잡한 비선형 방정식이다. 진동분석을 간편히 하기 위해 비선형 방정 식을 선형화하였고^[17] 선형화된 방정식은 아래와 같이 표현된다.

여기서

m는 엔드이펙터 질량이고 Iz는 평면에 수직인 방향의 회전모멘트이다. 강성행렬 K는 각 케이블의 강성 k1, k2, k3, k4의 조합으로 이루어진 3×3대칭행렬이다.

3. 평면형 케이블 로봇의 고유진동수

평면형 케이블 로봇에서의 로봇 구조에 따른 진동수 변화분석을 하기 위해 고유진동수를 구하였다. 식 (8)은 x, y, θ가 결합된 연결방정식이므로 강성행렬에 대한 질량 정규화를 하였다^[18].

식 (10)에서 표시된 질량 정규화된 강성행렬은 MATLAB 의 eigenvalue 함수로 고유치를 구하고 고유치의 제곱근 으로 고유진동수를 계산하였다. 엔드이펙터가 작업범위 내의 임의의 위치에 있을 때 계산된 고유진동수의 정확 성을 검증하기 위해 시뮬레이션 소프트웨어 MSC ADAMS 와 계산결과를 비교하였다. 프레임 형상을 정방형으로 정하고(가로×세로=4 m×4 m) 엔드이펙터 형상을 장방 형으로 정하였다(가로×세로=0.4 m×0.2 m). 엔드이펙터 질량 m를 5 kg이라고 가정하면 평면에 수직인 축에 대 한 질량 모멘트 I_z는 0.0833 kg.m²이였다. 비교의 일반성 을 얻기 위해 임의의 2개 자세를 취하였고 Table 1에서 이에 대한 파라미터를 보여주고 있다. 그 중 pose1은 엔 드이펙터의 초기상태가 회전되지 않았고 pose2는 회전 된 것이다. 비교한 결과 Table 2에서와 같이 본 논문에 사용된 고유진동수 계산 방법은 ADAMS 시뮬레이션 결 과와 잘 일치했다.

Table 1

End-effector poses and cable stiffness parameters

Table 2

Comparison of natural frequencies between a mathematical model by MATLAB and a numerical model by ADAMS

4. 케이블 로봇 진동분석

서론에서 언급했듯이 본 연구는 진동에 강한 평면형 케이블 로봇 구조를 제안하는데 그 목적이 있다. 주변환 경의 낮은 진동수의 외란은 주로 1차 고유진동수에 영향 을 주어 로봇의 1차 고유진동수와 공진을 일으킬 수 있 다. 따라서 최대한으로 높은 1차 고유진동수를 가질 수 있게 로봇 구조를 설계해야 한다. 이 장에서는 케이블 로봇의 프레임 형상, 엔드이펙터 형상과 케이블 연결방 식을 변화하면서 작업공간 내의 1차 고유진동수를 계산 하여 진동에 강한 구조를 분석하였다. 평면형 4케이블 로봇의 경우, 프레임과 엔드이펙터의 형상으로는 주로 대칭성이 좋은 정방형과 장방형을 사용하고, 케이블 연 결방식은 Fig. 3과 같이 정상연결, 위아래 교차연결과 좌우 교차연결을 사용할 수 있다. 참고로, 본 논문에서 정의되는 프레임과 엔드이펙터의 형상의 케이블이 연결 되는 점이 그리는 형상을 기준으로 정의되었다. 고정된 프레임 면적과 엔드이펙터 면적에서 프레임과 엔드이펙 터 형상변화에 의한 진동을 분석하기 위해 프레임과 엔 드이펙터의 가로 세로 비율(P_Frame 와 P_EE)을 무차원 변 수로 설정하였다.

Fig. 3

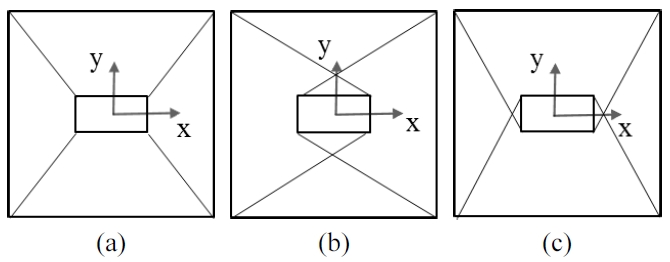
Cable connection methods: (a) Normal connection (b) Up-Down (U-D) cross connection (c) Left-Right (L-R) cross connection.

식 (11)에서 W_F, H_F는 프레임의 폭, 높이이고 W_F, H_F 는 엔드이펙터의 폭, 높이이다. 같은 값의 무차원 파라미 터 P_Frame 와 P_EE에서도 프레임과 엔드이펙터의 크기는 다를 수 있으며, 그 예로 W=4 m, H=1 m일 때와 W=200 m, H=50 m일 때 P=2²으로 동일할 수 있다. 또한, 프레임 면적과 엔드이펙터 면적 사이의 차이가 크고 작을 때 케이블 로봇 강성에 영향이 있을 수 있기 때문에 같은 엔드이펙터 면적에 작은 프레임과 큰 프레임 2가지로 나누어 분석했다. 한 예로 동일한 엔드이펙터 면적 0.02 m²에 프레임 면적을 400배 차이인 8 m²와 40000배 차이 인 800m²으로 선택하였다. 그 파라미터 들은 Table 3, 4(프레임)와 Table 5(엔드이펙터)에서 나타내고 있다. 그 중 W_LF, H_LF는 800 m²의 큰 프레임(Large frame)에 해당 되는 폭, 높이 이고 W_SF, H_SF는 8 m²의 작은 프레임(Small frame) 해당되는 폭, 높이이다. 프레임이 직사각형인 경 우 작업공간은 사분면이 대칭이므로 분석범위를 제1사 분면으로 선택하였다. 엔드이펙터 질량은 5 kg으로 하였 고, 평면에 수직인 축 방향에 대한 모멘트는 엔드이펙터 의 형상에 따라 결정 된다.

Table 3

Frame parameters of small frame (8 m2)

4.1. 로봇 구조에 따른 주요 영향

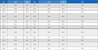
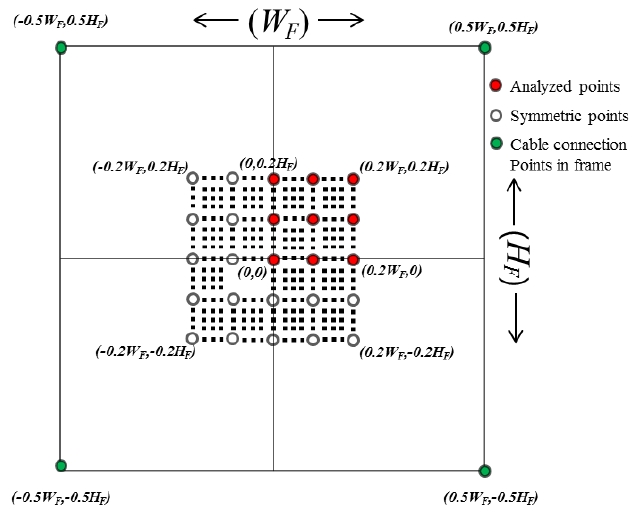
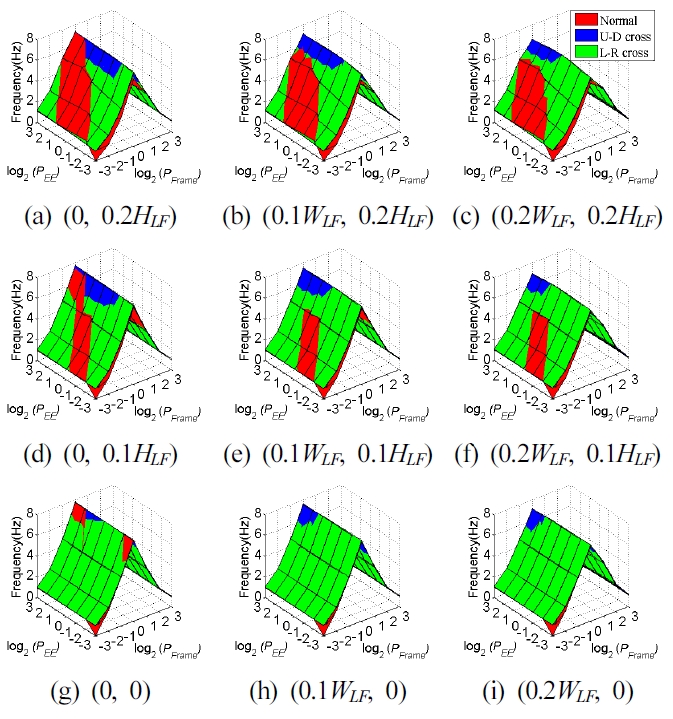
프레임 형상, 엔드이펙터 형상과 케이블 연결방식 중 에서 1차 고유진동수의 크기에 가장 큰 영향을 주는 인 자를 찾기 위해 엔드이펙터 중심이 Fig. 4에서와 같이 위치했을 때의 1차 고유진동수를 분석하였다. 엔드이펙 터의 위치가 Fig. 4의 9개 분석점(Analyzed points)에 위 치했을 때 Table 3, Table 4와 Table 5의 파라미터를 사용 하여 1차 고유진동수를 구하였고, 그 결과를 각각 Fig. 5와 Fig. 6에서 (a)부터 (i)까지 나타내었다. 본 그림에서 는 프레임과 엔드이펙터 크기 변화에 따른 1차 고유진동 수 변화를 효과적으로 나타내기 위해 log₂ 스케일을 사용 하였다. 예를 들면 log₂(P_Frame)이 2인 점은 프레임의 가로 세로 비율이 2², 즉 4:1인 점이다. Fig. 5의 경우 8m²의 작은 프레임일 때이고 Fig. 6은 800 m²의 큰 프레임일 때이다. Fig. 5와 Fig. 6에서 보면 프레임 형상변화에 의 한 1차 고유진동수 변화가 제일 크고 엔드이펙터 형상변 화와 케이블 연결방식의 변화로는 1차 고유진동수가 작 은 범위에서 변하므로, 프레임 형상이 주도적인 영향을 준다는 것을 알 수 있다. 큰 프레임의 1차 고유진동수와 작은 프레임의 1차 고유진동수 크기 는 다르지만 장방형 에서 정방형으로 가깝게 갈수록 1차 고유진동수는 모두 높아지는 경향을 볼 수 있다. 따라서, 정방형 프레임에서 1차 고유진동수가 제일 높으며 낮은 진동수의 외란의 영향도 적게 받는다.

Fig. 4

The distribution of analyzed points

Table 4

Frame parameters of large frame (800 m2)

Table 5

End-effector parameters

Fig. 5

Change of the first natural frequency according to end effector positions in small frame (8 m2 )

Fig. 6

Change of the first natural frequency according to end effector spositions in large frame (800 m2 )

4.2. 로봇 구조에 따른 세부적인 영향

4.2.1. 엔드이펙터 형상과 케이블연결방식에 의한 영향

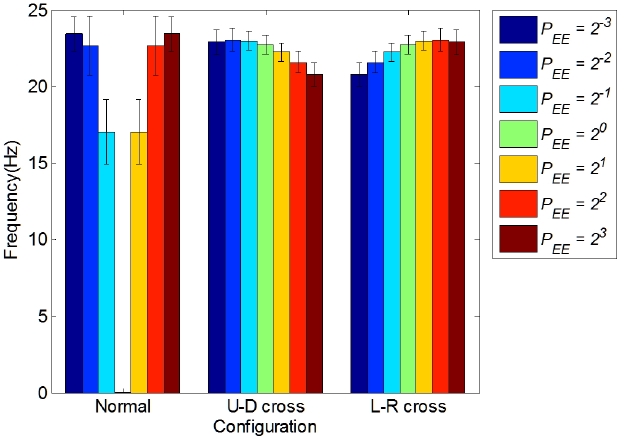
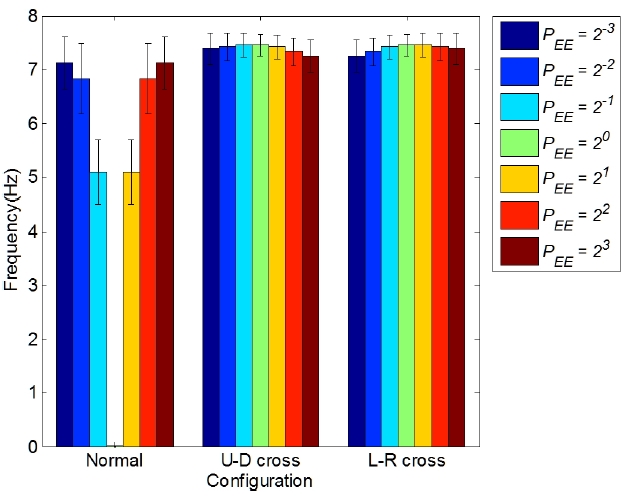
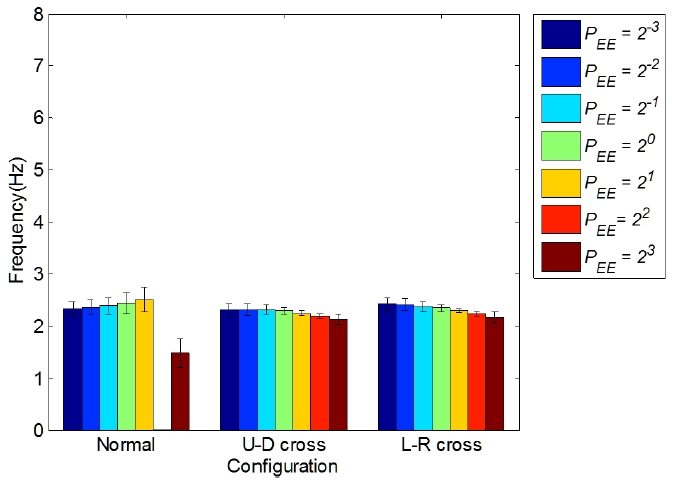
Fig. 5와 Fig. 6의 분석으로 케이블 로봇 구조에서 프레 임의 형상이 1차 고유진동수 크기에 주도적인 영향을 준다는 것을 알 수 있었다. 세부적으로 엔드이펙터 형상 과 케이블 연결방식이 1차 고유진동수 변화에 주는 영향 을 관찰하기 위해 프레임의 형상을 고정시키고 엔드이 펙터 형상과 케이블 연결방식을 변화하였다. 정방형 프 레임 일 때 1차 고유진동수가 제일 높지만 실제 상황에 서 정방형 프레임을 구현하기 어려울 수 있으므로 장방 형 프레임을 사용할 때의 엔드이펙터 형상변화에 따른 진동분석도 수행하였다. 작업공간 내에서 1차 고유진동 수가 높은 로봇 구조를 분석하기 위해 Fig. 4의 (0~0.2)W_F 와 (0~0.2)H_F내에서 121개 위치에 엔드이펙터 중심을 놓 고 1차 고유진동수 평균과 표준편차를 구하였다. 작고(8 m²) 큰(800 m²) 정방형 프레임(P_Frame=2⁰)과 장방형 프레 임(P_Frame=2²)에서 진동수변화 경향을 비교분석하기 위 해 작은 정방형 프레임, 큰 정방형 프레임, 작은 장방형 프레임, 큰 장방형 프레임에 대해 각각 분석을 수행하였 고 Fig. 7, 8, 9, 10은 그 결과를 나타내고 있다. 정방형 프레임일 때의 Fig. 7과 Fig. 8에서 보면 정상연결(normal connection) 상태에서의 정방형 엔드이펙터(P_EE=2⁰)와 정방형에 가까운 엔드이펙터(P_EE=2^-1과 P_EE=2¹)일 때를 제외하고 엔드이펙터 형상과 케이블 연결 방식에 따른 1차 고유진동수 차이는 작았다. 또한 엔드이펙터가 정방 형(P_EE=2⁰) 일 때 1차 고유진동수가 0을 갖게 되고 정방 형 부근 (P_EE=2^±1)일 때 1차 고유진동수는 다른 경우와 비교했을 때 크게 낮다는 것을 볼 수 있다. 이는 엔드이 펙터의 가로 세로 비율과 프레임의 가로 세로 비율이 같을 때(P_EE=P_Frame) 계산상 식 (8)에서 행렬의 계수(rank) 가 3에서 2로 떨어지는 특이점이 생기기 때문이다. 특이 점 부근에서 회전강성이 급격히 감소하여 1차고유진동 수가 낮아지며 해당모드의 진동이 쉽게 발생하게 된다. 일반적으로 정상연결은 구현하기가 간단하고 반면에 교 차연결은 케이블 간의 간섭 등의 문제로 하드웨어 제작 에 있어 추가적인 고려가 필요하게 된다. 따라서 정방형 프레임일 경우, 정방형 엔드이펙터로 인한 특이점의 영 향을 받는 영역은 교차연결을 사용하고 그 외에는 정상 연결을 사용하는 것이 적합하다.

Fig. 7

Mean frequencies with small square frame (8 m2, PFrame=20)

Fig. 8

Mean frequencies with large square frame (800 m2, PFrame=20)

Fig. 9

Mean frequencies with small rectangular frame (8 m2, PFrame=2 2 )

Fig. 10

Mean frequencies with large rectangular frame (800 m2 , PFrame=22)

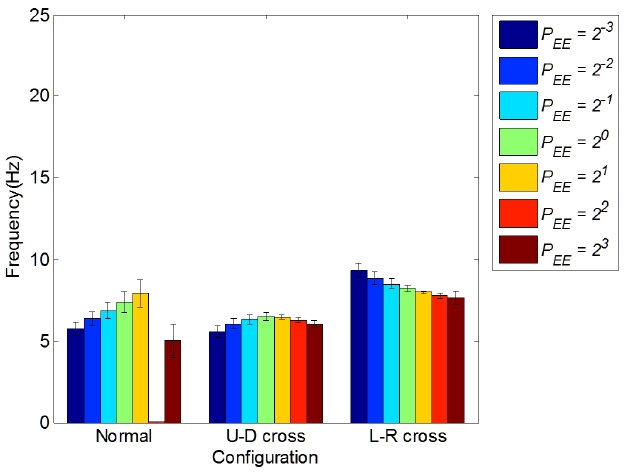
장방형 프레임일 때의 Fig. 9와 Fig. 10에서 보면 정상 연결에서 엔드이펙터의 가로 세로 비율과 프레임의 가 로 세로 비율이 같을 때(P_EE=P_Frame=2²) 1차 고유진동수 는 0을 갖게 된다. 큰 프레임(800 m²)에서 엔드이펙터 형상과 케이블 연결형태에 따른 고유진동수의 차이가 작지만 작은 프레임(8 m²)에서는 일정한 차이가 있었다 (높은 높이의 장방형 엔드이펙터(P_EE=2^-3)일 때 좌우 교 차연결(L-R cross)의 1차 고유진동수 평균이 정상연결의 약 1.5배). 폭이 넓은 엔드이펙터(P_EE=2¹)에서는 3가지 연결형태의 차이가 별로 없지만 엔드이펙터의 높이가 높아짐(가로 세로 비율(P_EE)이 작아짐)에 따라 정상연결 의 1차 고유진동수는 낮아지고 좌우 교차연결의 고유진 동수가 높아지기 때문이다. 따라서, 특이점 영향을 받는 영역을 피한 아래 조건일 때 작은 프레임(8 m²)에서는 엔 드이펙터가 긴 방향으로 교차하는 것이 좋고 (P_Frame=2ⁿ, P_EE=2^m이라고 가정하면 n>0일 때 m<n-5와 n<0 일 때 m>n+5) 나머지 경우는 정상연결을 하는 것이 적합하다. 큰 프레임(800m²)에서는 케이블 연결방식에 따라 1차 고유진동수의 차이가 작으므로 정상연결을 추천하되 특 이점 (P_Frame=P_EE)의 영향을 받는 영역은 피하여야 한다.

4.2.2. 정상연결 특이점의 영향 영역

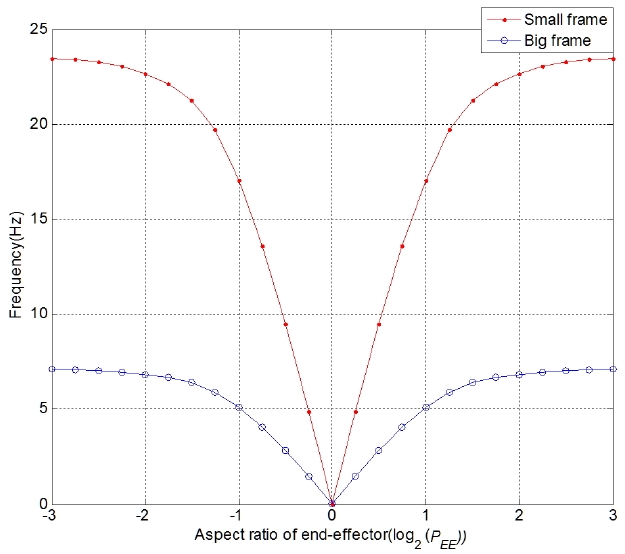
정방형 프레임(P_Frame=2⁰)과 장방형 프레임(P_Frame=2²) 에서 케이블을 정상연결 했을 때 생기는 특이점 영역을 분석하기 위해, 엔드이펙터 변화범위(P_EE=2^-3에서 P_EE=2³ 까지)를 log₂(P_EE) 스케일에서 25등분하여 1차 고유진동

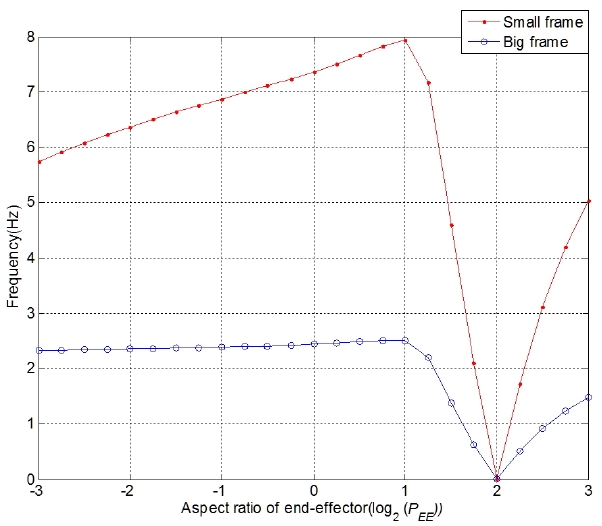
수를 계산하였다. Fig. 11과 Fig. 12에서 각각 정방형 프레임인 경우와 장방형 프레임인 경우 진동수변화에 대해 나타내고 있다. Fig. 11에서 보면 정방형 엔드이펙 터(P_EE=2⁰)에서 그 부근 (P_EE=2^±1.5)까지 1차 고유진동수 가 급격히 증가하고 장방형 엔드이펙터 P_EE=2^±1.5부터는 상승추세가 낮아 진다. Fig. 12에서 보면 장방형 프레임 (P_Frame=2²)에서는 엔드이펙터의 가로 세로 비율과 프레 임의 가로 세로 비율이 같을 때(P_EE=P_Frame=2²)의 양쪽으 로 1차 고유진동수는 급격히 증가하되 엔드이펙터의 폭 이 작아지는 쪽으로 더 빨리 증가하여 폭이 높이의 두배 일 때(P_EE=2¹) 최고치를 갖고 폭이 더 작아지면 점점 낮 아지는 추세를 갖는다. 따라서 정방형 프레임에서 특이 점의 영향을 받는 영역은 (2^-1.5≤P_EE≤2^1.5)이고 장방형 프레임에서 특이점의 영향을 받는 영역은(P_EE=2ⁿ, P_EE=2^m 일 때 n+1≥m≥n-1)이다.

Fig. 11

The first natural frequency with normal connection in square frame (PFrame=20)

Fig. 12

The first natural frequency with normal connection in rectangular frame (PFrame=22)

5. 결 론

본 논문에서는 일반적인 완전구속 평면형 케이블 로 봇에서 진동에 강한 구조를 설계하기 위해, 프레임의 형 상, 엔드이펙터의 형상과 케이블 연결방식에 따른 진동 분석을 수행하였다. 진동 분석은 프레임과 엔드이펙터 의 면적을 고정시키고 가로 세로의 비율을 무차원 파라 미터로 선정하여 엔드이펙터의 1차 고유진동수에 대한 분석을 수행하였다. 분석결과 프레임의 형상이 제일 큰 영향인자였고 정방형에 가까울수록 평면형 케이블 로봇 은 높은 1차 고유진동수를 갖게 되였다. 다양한 작업공 간에 적용 시 정방형 프레임을 구현하기 어려울 수 있으 므로 정방형 프레임과 장방형 프레임일 때 엔드이펙터 의 형상 선택과 케이블 연결방식의 영향에 대해 각각 분석하고 높은 1차 고유진동수를 가질 수 있는 구조를 제안하였다. 같은 P_EE, P_Frame에 프레임과 엔드이펙터의 크기가 다를 수 있으므로 그 영향을 고려하여 프레임을 큰 프레임과 작은 프레임으로 나누어 분석하였다. 분석 결과, 프레임 크기에 의해 1차 고유진동수의 크기 차이 는 있지만, 경향에는 큰 영향이 없었다. 따라서 큰 프레 임에서는 특이점의 범위를 제외한 엔드이펙터 형상과 케이블 연결방식에 따른 1차 고유진동수 차이가 작으므 로 무시할 수 있지만 프레임이 작을수록 엔드이펙터 형 상과 케이블 연결방식에 대한 영향이 크게 되므로 작은 프레임의 로봇구조 설계 시 이를 고려해야 한다. 향후 연구로 공간상 6자유도 케이블 로봇에서 주로 사용되는 케이블 연결방식을 선택하여 엔드이펙터 형상과 프레임 형상에 따른 진동분석으로 6자유도 케이블 로봇에서의 진동에 강한 구조 설계에 대한 연구를 수행할 예정이다. 또한 중력의 크기와 방향이 고유진동수에 어떤 영향을 미치는지에 대한 연구도 진행될 예정이다.

Acknowledgments

This research was supported by Leading Foreign Research Institute Recruitment Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (MSIP) (2012K1A4A3026740).

References

• Pott, A, Meyer, C, Verl, A, “Large-scale assembly of solar power plants with parallel cable robots”, 41st International Symposium on Robotics and 6th German conference on Robotics, (2010), Jun, p999-1004.
• Williams, R, “Five-hundred meter aperture spherical radio telescope (FAST) cable-Suspended robot model and comparison with the Arecibo observatory”, Internet publication, (2015), July.
• Albus, J, Bostelman, R, Dagalakis, N, “The NIST robocrane”, Journal of Robot Systems, (1993, Jul), 10(5), p709-724. [https://doi.org/10.1002/rob.4620100509]
• Jamshidifar, H, Fidan, B, Gungor, G, Khajepour, A, “Adaptive vibration control of a flexible cable driven parallel robot”, 15th IFAC Symposium on Information Control Problems in Manufacturing, (2015, Aug), 48, p1302-307. [https://doi.org/10.1016/j.ifacol.2015.06.265]
• Weber, X, Cuvillon, L, Gangloff, J, “Active vibration canceling of a cable- driven parallel robot in modal space”, IEEE International Conference on Robotics and Automation, (2015), May, p1599-1604. [https://doi.org/10.1109/icra.2015.7139402]
• Du, J, Bao, H, Cui, C, Yang, D, “Dynamic analysis of cable-driven parallel manipulators with time-varying cable lengths”, Finite Elements in Analysis and Design, (2012, Jan), 48, p1392-1399. [https://doi.org/10.1016/j.finel.2011.08.012]
• Shao, Z-F, Tang, X, Wang, L-P, You, Z, “A fuzzy PID approach for the vibration control of the FSPM”, International Journal of Advanced Robotic Systems, (2013, Jan), 10. [https://doi.org/10.5772/53278]
• Du, J, Duan, X, Qiu, Y, “Dynamic analysis and vibration attenuation of cable-driven parallel manipulators for large workspace applications”, Advances in Mechanical Engineering, (2013), 5. [https://doi.org/10.1155/2013/361585]
• Behzadipour, S, Khajepour, A, “Stiffness of cable-based parallel manipulators with application to stability analysis”, Journal of Mechanical Design, (2006), 128(1), p303-310. [https://doi.org/10.1115/1.2114890]
• Kawamura, S, Kino, H, Won, C, “High-speed manipulation by using parallel wire-driven robots”, Robotica, (2000, Sep), 18(1), p13-21. [https://doi.org/10.1017/s0263574799002477]
• Mukherjee, P, Dasgupta, B, Malik, A, “Dynamic stability index and vibration analysis of a flexible Stewart platform”, Journal of Sound and Vibration, (2007, Nov), 307(3), p495-512. [https://doi.org/10.1016/j.jsv.2007.05.036]
• Diao, X, Ma, O, “Vibration analysis of cable-driven parallel manipulators”, Multibody system dynamics, (2009, May), 21(4), p347-360. [https://doi.org/10.1007/s11044-008-9144-0]
• Liu, Z, Tang, X, Shao, Z, Wang, L, Tang, L, “Research on longitudinal vibration characteristic of the six-cable-driven parallel manipulator in FAST”, Advances in Mechanical Engineering, (2013), 5. [https://doi.org/10.1155/2013/547416]
• Tang, X, Liu, Z, Shao, Z, Wang, L, “Self-excited vibration analysis for the feed support system in FAST”, International Journal of Advanced Robotic Systems, (2014, Jan), 11, p1392-1399. [https://doi.org/10.5772/58521]
• Tang, AF, Li, Y, Kong, LF, Cheng, XJ, “Vibration analysis of tendon-based parallel robot for processing”, Advanced Materials Research, (2013, Jan), 655-657, p1086-1091.
• Kraus, W, Schmidt, V, Rajendra, P, Pott, A, “System identification and cable force control for a cable-driven parallel robot with industrial servo drives”, 2014 IEEE International Conference on Robotics & Automation, (2014), June, p5921-5926. [https://doi.org/10.1109/icra.2014.6907731]
• Piao, J, Jung, J, Seon, J-A, Park, S, Park, J-O, Ko, SY, “Simulation of effect of cable robot configuration on natural frequency”, IEEE International Conference on Mechatronics and Automation, (2015), Aug, p1828-1833. [https://doi.org/10.1109/icma.2015.7237764]
• Inman, D, Engineering Vibration, (2007), , Pearson Education, Inc, USA.