이동 로봇의 상대적 위치 추정을 위한 직사각형 기반의 기하학적 방법

1. 서 론

본 논문에서는 이동 로봇이 작업 환경의 특징을 이용 하여 자기 위치를 상대적으로 추정함에 있어^[1] 단일 영 상 기반에서 장면의 직사각형 특징을 활용하는 새로운 기법을 제시한다. 이동 로봇의 작업 환경이 실내이거나 인공물이 많은 공간일 경우 사각형 특징을 갖는 표식물 이 존재할 가능성이 높다. 예를 들어, 실내의 경우 출입 문이나 가구, 실외의 경우 간판, 외벽이나 창문이 이에 해당한다^[2,3,4]. 위와 같은 명시적인 사각형 외에도 선분 패턴이나 소실선 등에 의해 묵시적인 사각형이 정의되 기도 한다^[5]. 이러한 사각형 특징을 이용하여 이동 로봇 의 위치를 추정할 수 있다면 명시적으로 부착한 특별한 표식자나 센서에 대한 의존도를 줄일 수 있을 것이다.

하지만, 장면내 사각형을 이용하여 이동 로봇의 위치 를 추정하기 위해서는 몇 가지 해결할 문제들이 있다. 우선 계산이 간단하고 정확해야 한다. 만약, 단일 영상에 서 추출한 하나의 사각형에 간단한 대수식을 적용하여 위치를 추정할 수 있다면 바람직할 것이다. 반대로 bundle adjustment와 같은 방법은 특징의 기하학적 형태에 대한 사전 조건없이(예, 특징이 직사각형이라는 사실) 일반적 인 상황에서 장면을 복원하여 위치를 추정할 수 있지만 계산량이 매우 많은 방법으로 이동 로봇에는 적합하지 않을 수 있다^[6,7]. 또한, 장치적인 부담이 적어야 한다. 만약, 일반적인 웹 카메라 한대 만을 사용하고 카메라 캘리브레이션 및 특별한 마커의 사용이 필요없다면 실 용적인 면에서 매우 우수할 것이다.

본 논문에서는 이동 로봇의 위치 추정을 위해서 계산 량이 적고 장치적 부담이 적어야 한다는 제약조건을 만 족시키는 새로운 방법을 제시한다. 즉, 카메라에서 취득 한 단일 영상에서 종횡비가 알려져 있지 않은 사각형을 추출하여 이를 복원하고 그에 상대적으로 카메라의 위 치와 방위를 계산할 수 있는 방법이다. 이때 카메라는 단순한 기하학적 모델을 가정하며 캘리브레이션 정보를 사용하지 않는다.

제안된 방법은 기존의 기하학적 컴퓨터 비젼에서 주 로 활용하고 있는 절대 코닉(absolute conic)이나 호모그 라피 방법^[7,8]이 아닌 선분 카메라쌍(coupled line cameras, CLC)이라는 새로운 도구를 이용하고 있다^[9,10,11,12]. 특 히, 선분 카메라쌍은 직사각형 기반의 투사구조에 특화 되어 있기 때문에 유도된 해석해가 단순하여 구현이 매 우 용이하다.

본 논문의 구성은 다음과 같다. 먼저 2절에서는 이전 연구에서 소개된 선분 카메라쌍의 주요 이론을 설명한 다. 3절에서는 제안된 방법을 설명하고, 4절에서는 실험 결과를 제시하고, 5절에서 본 논문을 맺는다.

2. 선분 카메라쌍

기하 컴퓨터 비젼(geometric computer vision) 분야에 서 비교적 새로운 이론인 선분 카메라쌍은 직사각형을 촬영할 때 발생하는 특별한 투사구조를 기하학적 성질 에 기반하여 대수적으로 기술하고자 고안되었다^[9]. 최초 에는 직사각형을 투사하는 프로젝터에 대한 연구에서 직접적인 영감을 받았고^[13], 후속 연구에서 그 해가 효율 화 및 일반화 되어 발전하였다^[10,11,12]. 기존의 절대 코닉 (absolute conic)이나 호모그라피 방법과 달리 카메라 캘 리브레이션(예, 내부 인수 f)이나 장면 직사각형의 종횡 비에 대한 선행 지식 없이 투사 구조를 모델링 할 수 있는 것이 특징이다.

아래에서는 제안 방법에서 활용되는 CLC의 중요 이 론에 대해서 요약한다. 먼저 선분 카메라쌍은 카메라의 주축(principal axis)이 직사각형의 중심, 즉 두 대각산의 교점을 통과하는 특수한 경우를 기술하는 것에서 출발 하였다. 이를 위해서 처음 고안된 것은 1차원 이미지를 촬영하는 선분 카메라(line camera)이다. 선분 카메라 두 개가 주축을 공유하도록 결합하여 선분 카메라쌍을 정 의하게 된다. 주축이 사각형의 중심을 통과하지 않는 경 우는 전처리를 통해 CLC를 적용할 수 있다.

2.1. 선분 카메라

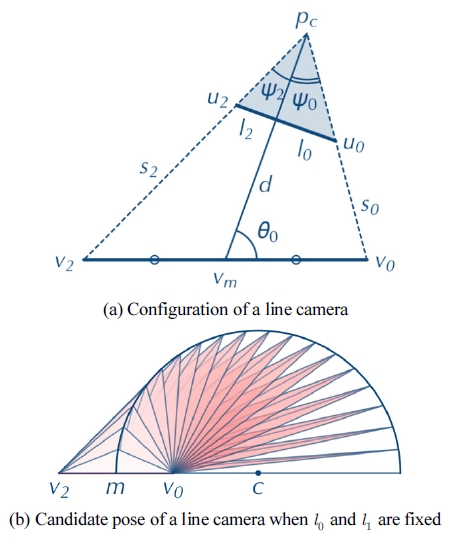
선분 카메라는 장면의 선분을 촬영하여 이미지 선분 을 생성하는 가상의 카메라이다. 즉, 선분 υ₀υ₂를 촬영하 면 이미지 선분 u₀u₂를 얻는다. 이때 주축은 항상 장면 선분 υ₀υ₂의 중심 υ_m을 통과한다. Fig. 1(a) 참조.

Fig. 1

Geometric configuration of a line camera[11]

주축이 이미지 선분 u₀u₂을 통과하여 l₀와 l₂의 비로 분할할 때 이를 이용하여 선분 카메라의 자세식을 아래 와 같이 정의할 수 있다.

$\[ \text{cos} {\theta }_0=d\frac{l_0\text{−}{l}_2}{l_0+l_2}=d{\alpha }_0 \]$

(1)

위 식에서 d는 주축의 길이, θ₀는 주축의 방위이며, α₀는 이미지 선분의 분할 계수이며 측정가능한 값이다. 특히, l₀와 l₂의 분할비가 알려져 있을 때 선분 카메라의 위치 P_c는 원 위에 존재함이 알려져 있다. Fig. 1(b)의 원주 위의 점 P_c와 선분 υ₀υ₂를 이용하여 선분 카메라를 정의할 때 그 분할 계수는 α₀로 고정되어 있다. 즉 원주 위의 어느점에서 선분을 촬영해도 l₀와 l₂의 분할비를 얻게 된다.

2.2. 선분 카메라쌍

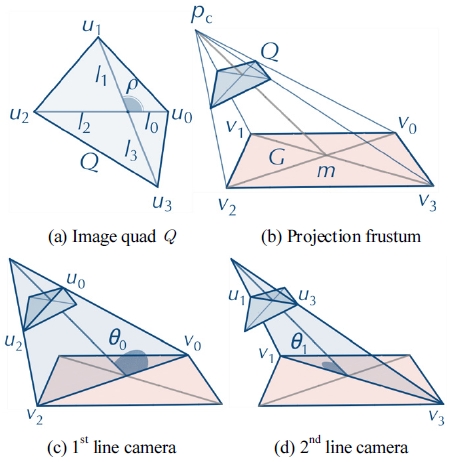
선분 카메라쌍은 두개의 선분 카메라를 직사각형 G의 대각선에 배치하여 정의할 수 있다. 이 때 영상으로 일반 사각형 Q가 얻어진다. Fig. 2 참조. 이 때 두 선분 카메라 가 주축을 공유하므로 주축의 길이 d와 카메라의 위치 P_c는 동일한 값을 갖게 되며 각 선분 카메라의 방위 θ₀와 θ₁은 독립적으로 정의된다. 또한 두 선분 카메라의 분할 계수 α_i도 독립적으로 정의된다.

Fig. 2

Configuration of coupled line cameras (CLC)[9-11]

위 구성을 선분 카메라의 자세식을 이용하여 다음과 같이 표현할 수 있다.

$\[ d=\frac{\text{cos} {\theta }_0}{{\alpha }_0}=\frac{\text{cos} {\theta }_1}{{\alpha }_1} \]$

(2)

$\[ \beta =\frac{l_1}{l_0}=\frac{\text{sin} {\theta }_1\left(d\text{−cos} {\theta }_0\right)}{\text{sin} {\theta }_0\left(d\text{−cos} {\theta }_1\right)} \]$

(3)

식 (2)는 두 선분 카메라가 주축을 공유하도록 하며, 식 (3)은 두 선분 카메라의 상대적 크기를 맞춰주는 역할 을 한다.

식 (2)와 (3)은 선분 카메라쌍의 자세식에 해당한다. 즉, 이미지 사각형 Q의 대각선의 분할비 l_i를 알고 있다 면 카메라의 자세를 결정하는 d와 θ_i를 계산할 수 있음 을 의미한다. 먼저 는 아래의 대수식으로 표현가능하다.

$\[ \begin{array}{l}d=\sqrt{\frac{A_0}{A_1}}\\ A_0={\left(1\text{−}{\alpha }_1\right)}^2{\beta }^2\text{−}{\left(1\text{−}{\alpha }_0\right)}^2\\ A_1={\alpha }_0^2{\left(1\text{−}{\alpha }_1\right)}^2{\beta }^2\text{−}{\left(1\text{−}{\alpha }_0\right)}^2{\alpha }_1^2\end{array} \]$

(4)

위에서 α_i는 식 (1)에 정의되어 있으며, β=l₁/l₀이다. 즉 식 (4)는 관찰된 이미지 사각형 Q의 대각선의 분할비 l_i만으로 카메라의 주축의 길이가 결정됨을 의미한다. 또한 식 (4)는 대각선 분할비를 통해 관찰된 이미지 사각 형 Q가 직사각형의 이미지인지를 판별할 수 있게 한다. 즉, A0A1>0의 조건을 만족시키지 않으면 직사각형으로 부터 투사된 이미지가 아니라고 판별할 수 있다. 식 (4) 는 중심 사각형의 대수적 일반해에 해당하며 투사 이미 지로부터 직사각형 여부를 판별하는 필요충분조건에 해 당한다. 식 (4)는 선분 카메라쌍의 대수해의 일부로 자세 한 유도과정은 이전연구^[9,10,11]에 설명되어 있다.

식 (4)를 통해 공유 주축의 길이 d를 알고 있으면 식 (1)의 선분 카메라 자세식을 이용하여 각 선분 카메라의 방위 θ_i를 계산할 수 있다. 다음으로는 이미지 사각형 Q의 대각선의 사이각 ρ를 이용하여 장면 직사각형 G의 사이각 ϕ를 아래의 대수식으로 계산할 수 있다.

$\[ \text{cos}\phi =\text{cos}\rho \text{sin}{\theta }_0\sin {\theta }_1+\text{cos}{\theta }_0\text{sin}{\theta }_1 \]$

(5)

사이각 ϕ는 직사각형의 종횡비를 결정하므로 이 과정 에서 직사각형이 복원된 것으로 볼 수 있다. 마지막으로 카메라의 위치 p_c를 아래의 대수식으로 계산할 수 있다.

$\[ \begin{array}{l}{p}_c=\frac{d}{\text{sin}\phi }\left(\text{sin}\phi \text{cos}{\theta }_0,\text{cos}{\theta }_1\right)\\ \text{−cos}\phi \text{cos}{\theta }_0, \text{sin}\rho \text{sin}{\theta }_0\text{sin}{\theta }_1\end{array} \]$

(6)

한가지 주의할 것은 p_c의 좌표계는 복원된 장면 직사 각형 G에 대해서 상대적으로 결정된다는 점이다. 즉, 사 각형의 중심 m=(0,0,0)을 원점으로 하고 첫번째 꼭짓 점 υ₀=(1,0,0)과 두번째 꼭짓점이 υ₁(cosϕ, sin ϕ,0)이 xy평면 위에 결정된다.

이 절에서는 카메라의 주축이 장면 직사각형 G와 이 미지 사각형 Q의 중심을 통과하는 특수한 경우에 대해 서 선분 카메라쌍을 정의하고 그 자세식을 이용하여 관 찰된 이미지 사각형 Q의 속성 (l_i와 d)에서 알려지지 않 은 장면 직사각형 G를 복원하고 카메라의 위치 p_c를 계 산하는 방법을 설명하였다.

2.3. 비중심 직사각형의 처리

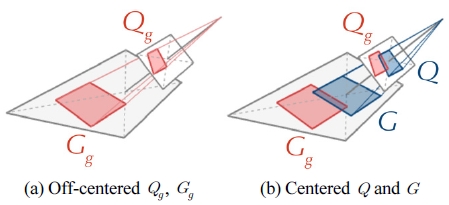
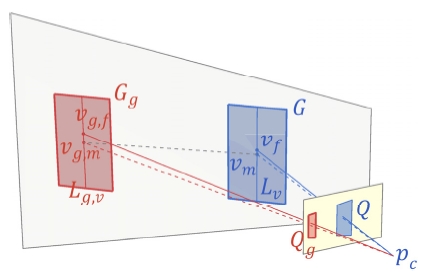
Fig. 3에서 장면에 종횡비가 알려지지 않은 직사각형을 G_g라고 하자. Fig. 3 참조. 이를 영상에서 추출하면 Q_g가 된다. 일반적으로 카메라의 주축은 장면 직사각형의 중 심을 통과하지 않는다. 따라서 2.2절의 선분 카메라쌍 기반 직사각형 복원 및 카메라 캘리브레이션방법을 적 용하기 위해서는 먼저 Q_g로 부터 특별한 직사각형 Q를 유추해야 한다.

Fig. 3

Application of CLC for an off-centered case

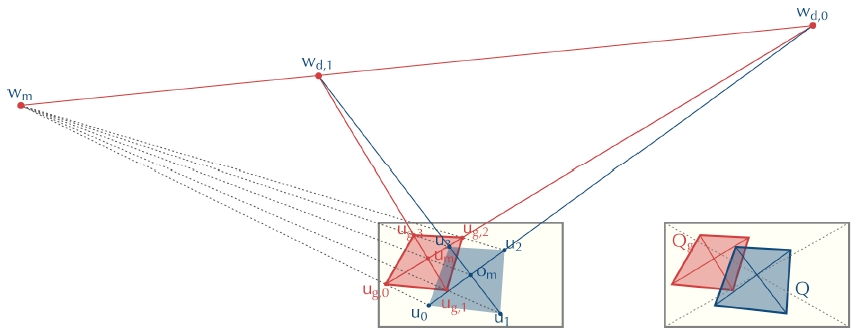
즉 Q는 장면내 가상 (proxy) 직사각형 G의 투사 이미 지며 카메라의 주축은 G와 Q의 중심을 통과한다. 또한, 직사각형 G와 G_g는 합동이다. 이전 연구 ^[11]에는 주어 진 사각형 Q_g로부터 가상 중심 사각형 를 유추하는 방법 이 자세히 설명되어 있다. 계산 과정은 순차적인 선분 교차 연산만으로 구성되어 있어서 매우 간단한 편이다. 이를 기하학적으로 도해하면 Fig. 4와 같다. 최근에는 비중심 사각형에 투영기하의 성질(projective conjugate harmonic)을 적용한 새로운 계산 방법이 발견되기도 하 였다^[14].

Fig. 4

Geometric method to infer a centered quad from an off-centered quad[11]

최종적으로 중심 사각형 G로부터 관심 직사각형 G_g 까지의 이동 벡터 υ_mυ_g,m도 기하학적으로 계산할 수 있다. 즉, 중심 이미지 사각형 Q와 중심 직사각형 G가 정의된 상황에서 perspective-to-Euclidean 변환을 사용하게 된 다. 이 변환을 통해 이미지의 좌표를 평면의 좌표로 변환 할 수 있고, 반대의 과정에서는 Euclidean-to-perspective 변환을 사용하게 된다. 이는 기존의 방법에서 호모그라 피를 이용한 평면간 변환에 해당한다^[7,8].

일련의 과정에서 카메라에 대한 캘리브레이션, 장면 직사각형의 종횡비 정보를 전혀 사용하지 않았고, 기존 의 호모그라피 방법도 사용하지 않은 것이 선분 카메라 쌍을 이용한 직사각형 투사구조의 복원의 중요한 특징 이라고 할 수 있다.

3. 이동 로봇의 사각형 기반 위치추정

3.1. 문제 정의

본 논문에서 다루는 이동 로봇의 위치 추정 문제는 평면에서 이동하는 로봇에 부착된 카메라로 촬영한 영 상 한장에서 사각형 영역을 추출하여 이에 해당하는 장 면내 직사각형으로부터 로봇까지의 상대적인 거리 및 방위를 계산하는 것이다. Fig. 5 참조.

Fig. 5

Geometric configuration of rectangle-based localization

카메라의 위치 p_c가 로봇의 위치를 대표한다고 하자. 예를 들어 p_c에 위치한 이동 로봇이 기하학적 정보가 알 려지지 않은 장면내 출입문 G_g의 정면 가운데로 이동해 야 하는 경우, G_g가 촬영된 영상에서 해당 이미지 사각형 Q_g를 추출하여 이로부터 로봇과 출입문과의 상대적 위 치를 계산해야 한다. 아래에서는 이를 위한 계산방법을 제시한다.

4. 실험 및 토의

제안된 방법은 간단한 대수적 해를 갖는 선분 카메라 쌍 기반 장면 복원 방법에 몇 가지 벡터 연산을 추가하여 이동 로봇의 상대 위치를 계산할 수 있으므로 전체적인 계산은 매우 효율적이다. 아래에서는 본 방법을 적용한 실험 결과를 소개한다.

4.1. 예제 영상에 적용

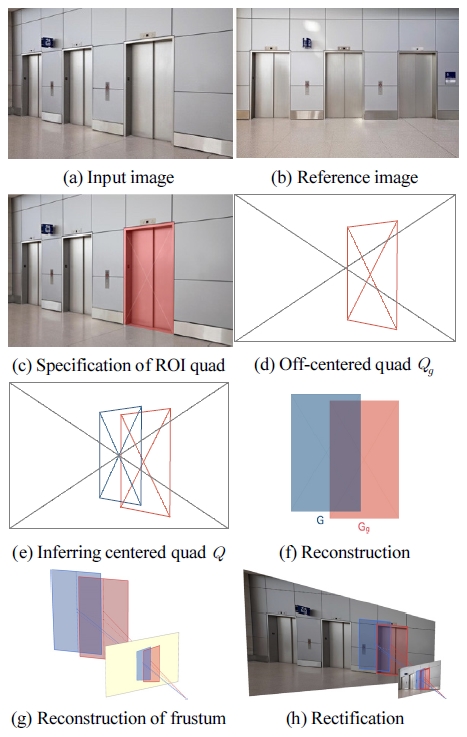
Fig. 6은 제안된 방법을 예제 영상에 적용한 예를 보여 준다. 이 예에서는 장면내 엘리베이터 문과 로봇의 상대 적 위치를 계산한다. 입력 영상 Fig. 6(a)와 참조 영상 Fig. 6(b)는 구글 이미지 검색을 통해 얻었으며 촬영한 카메라 정보는 알려져 있지 않다. 선분 카메라쌍의 가정 에 따라 주축이 영상의 중심을 통과하는 핀홀 카메라 모델로 가정하였다.

Fig. 6

Illustrative example of the proposed method

Fig. 6(c)는 입력 영상 6(a)에서 관심 사각형을 검출할 결과이다. 이후 계산 과정에서는 영상을 따로 활용하지 않고 Fig. 6(d)에서처럼 검출 사각형의 기하학적인 표현 Q_g를 계산에 이용하게 된다. Fig. 6(e)는 선분 카메라쌍 기반 복원 방법을 적용하기 위해 Q_g로부터 중심 사각형 Q를 추출한 결과이다. Fig. 6(f)는 중심 사각형 Q에 선분 카메라쌍을 적용하여 계산한 중심 직사각형 G이고 perspective-to-Euclidean 변환을 통해 Q_g로 부터 계산한 최종 목표 직사각형 G_g이다. Fig. 6(g)는 최종적으로 카 메라의 투사 구조를 복원한 결과이다. Fig. 6(h)는 주어 진 영상을 rectify한 예이다.

Fig. 6(g)와 같이 선분 카메라쌍에 의한 최종 복원이 완료된 상황에서 3.2절에서 소개된 위치 추정 방법을 적 용하면 방위 ψ =5.9279 및 거리 d_g,f=4.1324를 얻을 수 있었다. Fig. 6(b)의 참조영상이 출입문에 대한 정면 영 상이라고 가정하고, Fig. 6(a)로부터 복원된 직사각형과 의 종횡비(≈1.6916)를 비교했을 때 0.4%의 차이가 발생 하여, 제안된 전반적인 계산은 신뢰할 수 있다고 볼 수 있다. 다만 이 예에서는 인터넷에서 구한 영상을 사용하 였기 때문에 실제 카메라의 위치를 알 수 없지만 다음절 의 시뮬레이션 실험에서 계산의 정확성을 확인 할 수 있었다.

위 계산 과정은 Mathematica 10.2.0에서 구현되었고 OS X 10.11.2 환경에서 실험하였다. 계산 시간은 Q_g가 추출된 이후부터 위치 추정을 위한 방위 ψ와 거리 d_g,f를 계산할 때까지 0.001초 미만으로(2.8 GHz Intel Core i7 프로세서 기준), 실제 로봇 하드웨어에서 실시간에 계산 하기에 무리가 없을 것이다.

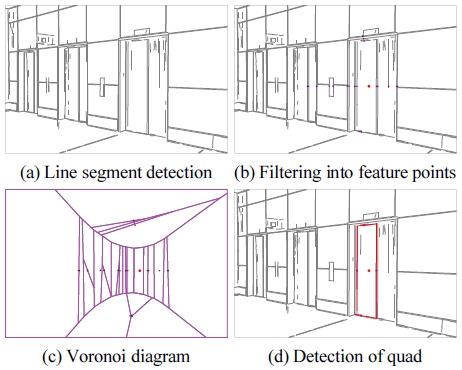
이 방법을 실제 이동 로봇에 적용하기 위해서는 촬영 된 영상에서 해당 이미지 사각형 Q_g를 추출하는 과정이 먼저 선행되어야 한다. Fig. 6(c) 참조. 이를 위한 구체적 인 계산 방법은 본 논문의 주제에서 벗어나서 구체적으 로 다루지는 않다^{[15,16,17,18]}. 본 논문에서는 자동 사각형 검출을 위해서 선분 검출 ^[19]와 보로노이 다이어그램을 이용한 기하학적 방법을 적용하고 있다. Fig. 7 참조. 기하 학적 자동 검출 방법은 수동 검출 또는 형태학(morphology) 기반의 검출에 비해 정밀도가 우수함이 알려져 있다^[20].

Fig 7

Automatic extraction of image quad: an example

4.2. 시뮬레이션 결과

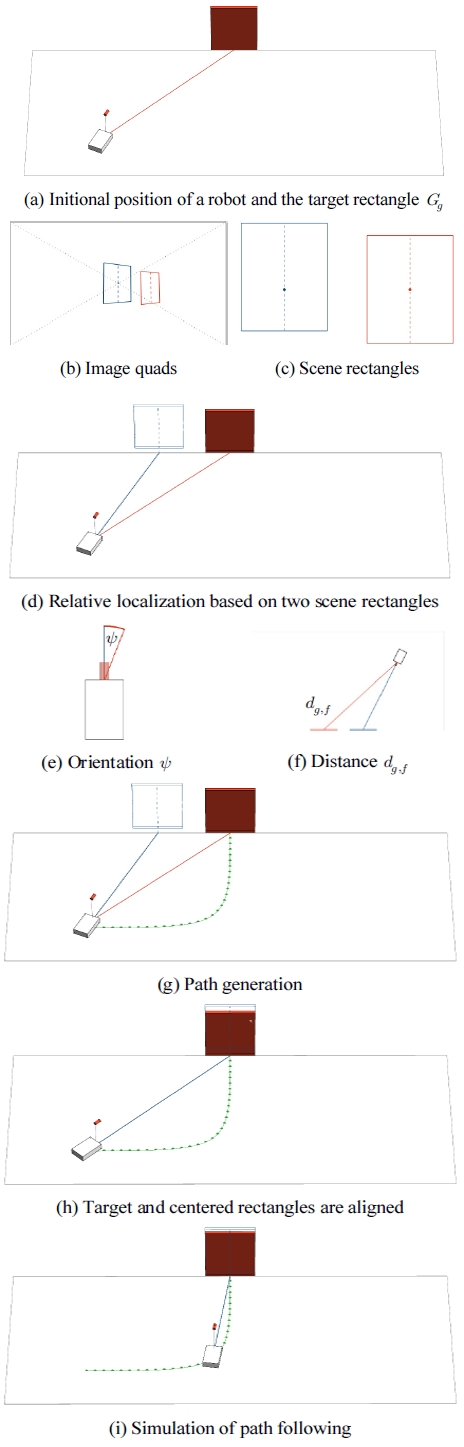
시뮬레이션 장면에서의 이동 로봇의 위치 추정 결과 를 제시한다. 본 시뮬레이션은 제안 방법을 고안하게 된 주요 동기가되는 시나리오에 기반한다. 즉, 물류로봇이 전역지도나 명시적 마커에 의존하지 않고 엘리베이터와 같은 출입문으로 진입함에 있어 출입문을 표현하는 직 사각형을 검출하여 제안 방법을 이용하여 상대 위치를 추정하고 비주얼 서보잉 방식으로 경로추종을 할 수 있 음을 보인다. 시뮬레이션은 4.1절과 동일하게 Mathematica 10.2.0 및 OS X 10.11.2 환경에서 수행되었다. 기본적인 환경은 Fig. 8(a)과 같다.

시뮬레이션에 사용한 이동 로봇은 가상의 로봇으로전 방향 이동이 가능하다고 가정한다. 로봇의 전면 상단에 카메라가 부착되어 있고 이를 통해 장면에 직사각형(붉 은색 문)에 대한 영상을 촬영하여 사각형을 검출하게 된 다. 시뮬레이션이므로 사각형의 검출은 정확한 계산이 가능하다. 실제 영상에서는 Fig. 7과 같은 자동 검출을 사용한다.

Fig. 8(b)-(c)는 Fig. 6과 유사하게 검출된 영상 사각형 에 선분 카메라쌍 방법을 적용한 결과를 보인다. Fig. 8(b)에서 붉은색 사각형 Q_g는 검출된 출입문이며 파란색 사각형 Q는 Fig. 4의 방법으로 유추한 중심사각형이다. 선분 카메라쌍 방법을 적용하면 Fig. 8(c)와 같이 직사각 형을 복원할 수 있다. 푸른색 직사각형이 복원된 가상 중심 직사각형 G이고, 붉은색 직사각형 G_g가 목표 직사 각형으로 출입문에 해당한다.

Fig. 8

Simulation of a moving logistics robot based on relative localization of the proposed method

Fig. 8(d)-(f)는 직사각형 출입문을 기준으로한 상대적 인 위치 추정의 결과를 보여준다. Fig. 8(d)에서 현재 위 치에서의 카메라 주축을 파란색 선으로, 목표 출입문의 중심까지를 붉은색 선으로 보여주고 있다. 이때 두 선은 로봇의 이동 평면에 투사된 상태이며 이 상태에서 방위 를 결정하게 된다. Fig. 8(e)는 이동 평면의 수직방향에서 로봇을 중심으로 Fig. 8(d)를 그린 것으로 파란색 주축과 붉은색 방위선 사이의 각도 ψ가 목표 직사각형을 중심 으로 한 로봇의 상대적 방위가 된다. Fig. 8(f) 역시 Fig. 8(e)를 이동 평면의 수직방향에서 그린 것으로 로봇과 출입문을 모두 표현하였다. 붉은색 선이 출입문의 중심 에서 로봇까지의 거리를 나타내고 있다.

이 때 위치 추정의 결과는 거리기준으로 오차 e≪10^-6 이내로 매우 정확한 결과를 준다. 이 수치는 목표 직사각 형의 크기에 대한 상대적인 크기이며 Fig. 8의 예에서는 다음과 같이 구하게 된다. 장면의 원점 (0,0,0)은 목표 직사각형과 바닥이 만나는 곳의 중심이다. 이동 로봇의 기준 좌표는 p_r=(x_r, y_r,0)이고 제안 방법으로 구한 측정 좌표는 p_m=(x_m, y_m,0)이라고 하자. 이 때 측정좌표는 선 분 카메라쌍의 좌표계에서 장면 좌표계로 변환하여 얻게 된다. 이 때 오차는 e|p_r-p_m|로 계산한다. Fig. 8(d)에 서의 실제 오차는 3.55612×10^-12이고상대오차는 5.93888× 10^-14이다.

이 위치 추정의 결과를 이용하여 가용한 경로 생성 및 추정 알고리즘에 적용한 예를 보여준다. Fig. 8(g)는 베지어 곡선을 이용하여 로봇의 현재 위치에서 목표 직 사각형의 중심까지의 경로를 생성한 예를 보여준다. Fig. 8(d)에서 최초의 로봇은 그 진행 방향(청색선)이 목표 직사각형의 방향(적색선)과 차이가 있다. 이는 위치 추 정 과정에서 계산된다. (이 예에서는 ψ=20.5°.) Fig. 8(h) 에서는 로봇이 목표 직사각형의 중심으로 회전을 한 경 우를 보여준다. 이 때 가상 중심 직사각형이 목표 직사각 형과 수선의 발 관점에서 일치함을 보여준다. Fig. 8(i)는 이러한 조건을 만족하며 이동 로봇이 경로를 추정하는 예를 보여준다.

4. 결 론

이동 로봇에 부착된 카메라로 장면에 존재하는 직사 각형 특징을 촬영하고 이를 이용하여 이동 로봇의 상대 적 위치를 추정하는 기하학적 방법을 제안하였다. 특히, 장면내 직사각형의 종횡비를 모르는 경우에도 캘리브레 이션되어 있지 않은 카메라로 촬영한 한장의 영상을 통 해 위치를 추정할 수 있음을 보였다. 제안 방법은 기하학 적 컴퓨터 비젼 분야의 선분 카메라쌍 이론에 근거하므 로 직관적인 기하학적 해석이 가능하고 간단한 대수해 에 기반하므로 계산이 효율적이다. 실험에서는 실제 이 미지 및 시뮬레이션에 제안 방법을 적용해 보았다.

향후에는 실제 이동 로봇에 제안 방법을 적용하여 위 치 추정 및 주행에 활용할 계획이다^[20,21]. 이를 위해서는 우선 영상내 사각형 특징을 실시간에 추출할 수 있는 정확하면서도 효율적인 방법을 발굴하여 결합하는 것이 필요하다. 현재는 [22]의 방법을 사용하고 있으나 아직 실시간 성능에는 못 미치고 있다. 또한, 복잡한 환경으로 인한 불확실성과 영상 품질 저하에 강건하게 대응할 수 있는 방법이 필요하다^[23,24]. 예를 들어 식 (4)의 판별식의 엄밀함을 완화하여 선분 카메라쌍의 근사해를 주는 것 이 필요하다.

또한, 제안된 직사각형 기반의 위치 추정 기법은 방법 은 팬-틸트 모터로 제어되는 기구부와 결합한 카메라-프 로젝터 시스템의 캘리브레이션과 제어에도 활용될 예정 이다^[25].

사 사

본 연구는 MOTIE/KEIT의 로봇산업 융합 핵심기술 개발사업(10048920, 10051155) 및 MSIP/IITP의 IT SW 융합산업 원천기술 개발사업(10041743)의 지원을 받아 수행되었습니다.

References

• Se, Stephen, David, Lowe, Jim, Little, “Mobile robot localization and mapping with uncertainty using scaleinvariant visual landmarks”, The international Journal of robotics Research, (2002), 21(8), p735-758. [https://doi.org/10.1177/027836402761412467]
• Shaw, David, Nick, Barnes, “Perspective Rectangle Detection”, In Proc. of the Workshop of the Application of Computer Vision in conjunction with ECCV 2006, (2006).
• Hartl, Andreas, Gerhard, Reitmayr, “Rectangular target extraction for mobile augmented reality applications”, Pattern Recognition (ICPR), 2012 21st International Conference on, (2012), p81-84.
• Korah, Thommen, Christopher, Rasmussen, “2D lattice extraction from structured environments”, In Image Processing 2007. ICIP 2007. IEEE International Conference on. IEEE, (2007), 2, pII-61. [https://doi.org/10.1109/icip.2007.4379092]
• Elloumi, Wael, Sylvie, Treuillet, Rémy, Leconge, “Realtime camera orientation estimation based on vanishing point tracking under Manhattan World assumption”, Journal of Real-Time Image Processing, (2014), p1-16.
• Triggs, Bill, Philip, F, McLauchlan, Richard, artley, I, Andrew W, Fitzgibbon, “Bundle adjustment—a modern synthesis”, Vision algorithms: theory and practice, (2000), Springer Berlin Heidelberg, p298-372. [https://doi.org/10.1007/3-540-44480-7_21]
• Szeliski, R, Computer Vision: Algorithms and Applications, (2010), Springer.
• Hartley, R, Zisserman, A, Multiple View Geometry in Computer Vision, (2003), Cambridge University Press.
• Lee, J-H, “Camera Calibration from a Single Image based on Coupled Line Cameras and Rectangle Constraint”, In Pattern Recognition (ICPR) 2012 21st International Conference on, (2012), p758-762.
• Lee, J-H, “A New Solution for Projective Reconstruction Based on Coupled Line Cameras”, ETRI Journal, (2013), 35(35), p939-942. [https://doi.org/10.4218/etrij.13.0213.0087]
• Lee, J-H, “New Geometric Interpretation and Analytic Solution for Quadrilateral Reconstruction”, In Pattern Recognition (ICPR) 2014 22nd International Conference on, (2014), p4015-4020. [https://doi.org/10.1109/icpr.2014.688]
• Lee, J-H, “Single View Reconstruction of Cuboids and Transformation in Perspective”, ETRI Technical Report, (2015).
• Lee, J-H, “An Asnalytic Solution to Projector Pose Estimation Problem”, ETRI Journal, (2012), 34(6), p978-981. [https://doi.org/10.4218/etrij.12.0212.0089]
• Lee, J, Lee, J-H, Kim, J, “Analysis on Coupled Line Cameras using Projective Geometry”, In PSIVT Workshop on Vision Meets Graphics Nov, (2015).
• Lagunovsky, Dmitry, Sergey, Ablameyko, “Straightline- based primitive extraction in grey-scale object recognition”, Pattern Recognition Letters, (1999), 20(10), p1005-1014. [https://doi.org/10.1016/s0167-8655(99)00067-7]
• Jung, C R, Schramm, R, “Rectangle Detection Based On A Windowed Hough Transform”, In Proc. 17th SIBGRAPI, (2004), p113 -120. [https://doi.org/10.1109/sibgra.2004.1352951]
• Zhang, Zhengyou, Li-wei, He, “Note-taking with a camera: whiteboard scanning and image enhancement”, Acoustics, Speech, and Signal Processing, 2004. Proceedings.(ICASSP'04). IEEE International Conference on, (2004), 3, piii-533, IEEE.
• Keller, Christoph Gustav, Christoph, Sprunk, Claus, Bahlmann, Jan, Giebel, Gregory, Baratof, “Real-time recognition of US speed signs”, In Intelligent Vehicles Symposium IEEE, (2008), 2008, p518-523, IEEE.
• von, Gioi, Rafael, Grompone , , “LSD: A Fast Line Segment Detector With A False Detection Control”, IEEE Transactions on Pattern Analysis & Machine Intelligence, (2008), 4, p722-732.
• Jung, M-K, Song, J-B, “Robust Global Localization based on Environment map through Sensor Fusion”, Journal of Korea Robotics Society, (2014), 9(2), p96-103. [https://doi.org/10.7746/jkros.2014.9.2.096]
• Hwan, H, Song, J-B, “Global Localization Based on Ceiling Image Map”, Journal of Korea Robotics Society, (2014), 9(3), p170-177. [https://doi.org/10.7746/jkros.2014.9.3.170]
• Lee, J-H, “Geometric Method for Detection of Image Quadrilateral”, In Circuits/Systems Computers and Communications (ITC-CSCC) the 30th International Technical Conference on, (2015), p482-48.
• Doucet, Arnaud, Simon, Godsill, Christophe, Andrieu, “On sequential Monte Carlo sampling methods for Bayesian filtering”, Statistics and computing, (2000), 10(3), p197-208. [https://doi.org/10.1023/A:1008935410038]
• Pomárico-Franquiz, Juan, Sanowar, H Khan, Yuriy, S Shmaliy, “Combined extended FIR/Kalman filtering for indoor robot localization via triangulation”, Measurement, (2014), 50, p236-243. [https://doi.org/10.1016/j.measurement.2013.12.045]
• Lee, A, Lee, J-H, Lee, J-H, “Sampling-based Control of SAR System Mounted on A Simple Manipulator”, Transactions of the Society of CAD/CAM Engineers, (2014), 19(4), p356-367. [https://doi.org/10.7315/cadcam.2014.356]