물체 운반을 위한 다수 로봇의 협조제어

1. 서 론

현대 사회의 지능형 로봇산업의 급속도의 성장으로 인하여 로봇의 역할과 수행이 증가하여 산업 현장뿐만 아니라 일상 생활에서도 많이 활용되고 있다^[1]. 로봇의 성능은 컴퓨터의 기술, 센서기술, 구동기 관련 기술 등 로봇관련 기술의 전반적인 발전으로 꾸준히 향상되어왔다^[2]. 특히, 단일 로봇의 성능 이상을 위하여 다수의 로봇을 이용하여 각 로봇이 주변 상황을 인식하고, 필요에 따라 하나의 목적을 위해 주위의 로봇과 협력하여 작업을 수행하는 군집 로봇 시스템에 대한 관심이 증대되고 있다^[3]. 최근 이동로봇의 연구는 로봇 한 대의 행동계획 에 대한 연구에서 다수 로봇의 행동 계획이나 협조에 관한 연구로 그 범위가 확대되고 있다^[4]. 다수의 로봇이 각자가 가진 능력만으로 해결하기 어려운 작업을 주위의 로봇들 간에 상호작용과 협력을 통해 주어진 작업을 원활하게 수행할 수 있도록 구성된 시스템을 군집로봇 시스템이라고 한다^[5]. 군집 로봇 시스템에서 주어진 목표를 달성하기 위한 필수 요소는 로봇들 간의 협력적인 공동 작업을 위한 전략이다. 최근 들어, 군집 지능이론은 집단 로봇 시스템의 설계화 구현에 새로운 접근 방법을 제공함으로써 상대적으로 간단한 구조를 가진 다수의 로봇들의 상호 협력을 통해 견실하고 유연한 방법으로 복잡한 임무를 수행할 수 있는 군집 로봇 시스템의 고성을 가능하게 하였다^[6]. 군집로봇 시스템의 기술은 군집행동제어 기술, 군집 상황인지 기술, 군집 네트워킹 기술, 군집 시스템 통합 기술 등 크게 4부분으로 분류될 수 있으며, 본 연구에서는 군집 로봇의 전체적인 시스템에 대해 기술하고자 한다. 상황과 행동은 주어져 있으며, 전체적인 움직임 방법과 통신 방법에 대해 연구하였다. 본 논문은 3대의 로봇이 하나의 물체를 운반 하기 위한 협조제어방법에 대해 연구 하였다. 논문의 구성은 다음과 같다. 본론에서 encoder 값을 이용해 로봇의 위치를 구하는 방법, 로봇이 물체를 들어올리기 위해 접근하는 거리를 고려한 머니퓰레이터의 경로계획에 대하여 설명한다. 결론에서 실제 실험을 통하여 얻은 결과 값을 통해 전체적인 시스템을 검증한다.

2. 이동 로봇의 제어

Figure 1은 실제 실험을 위해 제작된 로봇이다. 2개의 모터로 구동되며, Embedded Computer를 이용하여 제어하였다. 상단 머니퓰레이터는 서보 모터를 사용하였다. 로봇의 위치를 구하고, 선도-추종 방법을 이용하여 로봇을 제어하였다^[7,8].

Figure. 1.

Mobile robot

2.1. 위치 제어

모바일 로봇의 위치 인식 방법은 모바일 로봇의 몸체 중심점의 위치를 구해서 양쪽 바퀴의 위치를 구할 수 있도록 하였다. Fig. 2는 위치를 구하기 위해 모바일 로봇 하단부를 도식적으로 나타낸 그림이다. 그림과 같이 좌표계를 설정하면 모바일 로봇의 중심부 좌표 x_m, y_m 을 수식 (1)을 이용하여 구할 수 있다^[9,10].

Figure. 2.

Position of mobile robot

$$ \left(x_m,y_m\right)=\left(R\mathrm{\phi }\mathit{cos}\mathrm{\theta },R\mathrm{\theta }\mathit{sin}\mathrm{\theta }\right)$$

(1)

여기서 R 은 바퀴의 반지름 이며, φ 는 양쪽 바퀴의 평균 회전각도이고, θ 값은 몸체의 회전 각도이다.

$$ \mathrm{\phi }=\frac{1}{2}\left({\mathrm{\phi }}_r+{\mathrm{\phi }}_l\right)$$

(2)

φ_r 은 오른쪽 바퀴, φ_l 은 왼쪽 바퀴의 회전 각도이다.

몸체가 회전하는 경우 Fig. 3과 같이 도식적으로 나타낼 수 있다. 몸체의 회전은 양쪽 바퀴의 주행 거리가 다르다는 것을 활용하여 도식적으로 나타낸 것이다. 바퀴가 굴러가서 만든 원의 호의 길이는 θ 에 의한 원주의 길이와 같아야 한다. 따라서 수식 (3)으로 몸체의 회전 각도를 구할 수 있다. W 는 몸체 두 바퀴 사이 거리이다.

Figure. 3.

Rotation angle of mobile robot

$$ \mathrm{\theta }=\frac{R}{W}\left({\mathrm{\phi }}_r-{\mathrm{\phi }}_l\right)$$

(3)

2.2. Master-slave 모드 제어

3대의 모바일 로봇이 주행할 때 물체로 접근하고, 들어올리고, 운반하는 경우를 각각 고려할 필요가 있다. 따라서 아래와 같이 3가지 경우로 분류하고 그에 따른 제어 알고리즘을 구성하였다.

(1) 물체를 들고 있지 않은 경우

먼저 모바일 로봇이 물체를 찾아야 한다. 카메라와 초음파 센서 등을 이용하여 위치와 거리를 파악하는 단계가 되어야 하지만, 현재는 그에 대한 연구가 진행 중이므로 카메라 없이 물체의 위치를 정확히 알고 있다고 가정한다. 또한 모바일 로봇의 시작 위치 역시 알고 있다고 가정한다. 따라서 첫 번째 단계는 들어올려야 할 물체가 있는 곳으로 접근하는 것이다. 목표 위치와 시작 위치를 알고 있으므로 로봇이 쉽게 목표 위치로 접근이 가능하다.

(2) 물체를 들어올리는 경우

물체를 들어 올리기 위해서 역기구학 해석을 통해 머니퓰레이터의 움직임을 해석하였다. 물체를 들어올리는 동작에서 팔이 위로 올라갈수록 역기구학적으로 모바일 로봇이 물체 쪽으로 접근해야만 한다. 회전 동작은 존재 하지 않으며 오로지 필요한 거리만큼 접근만 한다. 따라서 물체를 들어 올릴 때의 모바일 로봇의 접근 거리를 역기구학 해석을 통해 고려하였다.

(3) 물체를 들고 움직이는 경우

물체를 완전히 들어 올리고 난 뒤에는 3대의 모바일 로봇이 동시에 같은 방향으로 움직여야 한다. 또한 로봇 사이의 거리 및 각도가 일정하게 유지되어야 한다. 로봇이 움직이는 속도 거리 방향이 모두 같아야지만 물체를 운반하는 과정에서 물체 파손의 위험 없이 안정적으로 운반 할 수 있다. 본 논문에서는 직선 주행만 실험하였다.

3대의 로봇은 1대의 Master 로봇과 2대의 Slave 로봇으로 구성되어있다. Master 로봇은 각 상황을 판단하여 Slave 로봇과 통신정보를 주고 받도록 되어있다. 로봇의 제어 알고리즘은 Fig. 4를 통해 볼 수 있다. 가장 먼저 3대의 로봇은 각자의 목표위치를 찾아가도록 한다. 3대의 로봇이 모두 정확한 위치에 도달하면, 로봇은 팔을 뻗어 물체를 잡는다. 이때 Slave 로봇들이 물체를 파지하는 동작을 완료하면 물체를 파지했다는 완료신호를 Master로봇으로 보낸다. Master로봇은3대의로봇이물체를잡았음을 확인하면 물체를 함께 들어올리도록 명령한다. Slave 로봇들이 동작을 완료하면 물체를 다 들어 올렸음을 Master로봇에게 완료신호를 보내고 Master로봇이 물체를 들어올렸음을 확인하면 다음의 주행동작을 위해 Master 로봇을 Leader로 Slave로봇을 Follower로 설정되어 목표 위치로 이동하는 알고리즘이다.

Figure. 4.

Behavior rule for swarm robots

물체를 들어 올린 것을 확인하면 그 위치를 Leader로봇을 기준으로 하여 현재의 거리와 각도를 유지하면서 주행하도록 한다.

로봇간의 위치를 유지하고 이동하기 위해 선도-추종방법을 이용하였다. 식 (4)을 이용하여 Fig. 5와 같이 한 대를 리더 로봇으로 정하고 리더로봇으로부터 각자의 위치를 계산 할 수 있다. 여기서 d_LF 는 Leader 로봇과 Follower 로봇 사이의 거리이다.

Figure. 5.

Leader-follower method for swarm robots

$$ \begin{array}{c}\mathit{LeaderP}\left(x_i,y_j\right)\\ \mathit{RP}\left(x_i,y_j\right)=\left[\left(x_i-d_{\mathit{LF}}\mathit{sin}\mathrm{\theta }\right),\left(y_i-d_{\mathit{LF}}\mathit{cos}\mathrm{\theta }\right)\right]\\ \mathit{LP}\left(x_i,y_j\right)=\left[\left(x_i-d_{\mathit{LF}}\mathit{sin}\mathrm{\theta }\right),\left(y_i+d_{\mathit{LF}}\mathit{cos}\mathrm{\theta }\right)\right]\end{array}$$

(4)

Fig. 6과 같이 리더 로봇을 따라 일정한 상대 위치를 유지하도록 하여 3대의 로봇이 리더로봇 방향으로 움직이도록 하였다. 리더 로봇으로부터의 위치를 유지하기 위해 Wi-Fi 통신을 사용하여 각각의 위치를 계산 하도록 하였다.

Figure. 6.

Driving method of swarm robots

2.3. 머니퓰레이터 제어

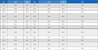
머니퓰레이터는 모바일 플랫폼의 상단에 장착되어 있으며 roll 축으로 회전이 가능하다. 3대의 로봇이 하나의 물체를 들어 올리는 협조작업을 위해서 end-effector의 위치를 파악해야 한다. Fig. 7과 같이 기구학적 모델링을 이용하여 end-effector의 좌표를 구할 수 있다^[11]. 기구학적 모델링은 D-H 방법을 이용하면 Table 1와 같은 DH table 2을 얻을 수 있다.

Figure. 7.

Behavior rule for swarm robots

Table 1.

D-H table

Table 2.

Parameter of Mobile Robot

물체를 집기 위한 정확한 목표지점을 알고 있다. 따라서 역기구학을 이용해 end-effector의 위치를 목표지점으로 옮기기 위해 역기구학을 이용한다. 따라서 아래의 식 (5)와 같은 동차 행렬을 구할 수 있다.

$$

(5)

한 측면에서 봤을 때 물체를 들어올리는 동작은 Fig. 8과 같이 붉은색 실선과 같은 사다리꼴 형태에서 두 대의 로봇이 접근함으로써 점선형태의 직사각형 형태로 변하면서 들어올려지는 형태로 볼 수 있다. 물체를 내려놓는 동작은 들어올리는 동작의 반대로 진행된다.

동차 행렬을 통해 x, y, z 값을 다음의 식 (6)~(8)과 같이 나타낼 수 있다.

Figure. 8.

Behavior rule for swarm robots

$$ x=\mathit{cos}{\mathrm{\theta }}_1\left(l_3\cos \left({\mathrm{\theta }}_2+{\mathrm{\theta }}_3\right)+l_2\cos {\mathrm{\theta }}_2\right)$$

(6)

$$ y=\sin {\mathrm{\theta }}_1\left(l_3\cos \left({\mathrm{\theta }}_2+{\mathrm{\theta }}_3\right)+l_2\cos {\mathrm{\theta }}_2\right)$$

(7)

$$ z=l_3\mathit{sin}\left({\mathrm{\theta }}_2+{\mathrm{\theta }}_3\right)+l_2\mathit{sin}{\mathrm{\theta }}_1+l_1$$

(8)

머니퓰레이터 end-effector의 시작 좌표와 목표 좌표가 주어지면 머 니퓰레이터의 좌표값을 계산할 수 있다. 여기서 목표 높이 z지점으로 이동하면서 변하는 x값의 변화를 통해 모바일 로봇이 접근하는 거리를 구할 수 있다.

동일한 모바일 머니퓰레이터 2대를 이용하여 하나의 물체를 들어 올리는 동작은 붉은 실선 형태의 사다리꼴 형태가 붉은 점선 형태의 사격형태로 바뀌면서 end-effector의 위치가 A에서 B로 이동하며 물체를 들어 올리게 되는 것이다. 머니퓰레이터의 움직임은 동일하다. 따라서 각 로봇의 관절은 서로 대칭을 이룬다. 따라서 평행사변형 형태에서 직사각형 형태로 바뀌는 동안 관절 각도의 합이 90° 임을 알 수 있다.

첫 번째 링크의 회전은 제자리에서 몸체만 회전하는 경우에만 일어나서 몸체 회전에도 불구하고 물체를 들고 있을 수 있도록 유지하게 된다. 따라서 다음의 수식 (9)를 얻을 수 있다.

$$ \begin{array}{c}{\mathrm{\theta }}_1=-\mathrm{\phi },\\ {\mathrm{\theta }}_2+{\mathrm{\theta }}_3={90}^{\mathrm{°}}\end{array}$$

(9)

머니퓰레이터 움직임에서 end-effector의 시작 위치와 목표 위치 역시 주어진 상태로 실험하였다. 또한 실험에서 몸체의 회전은 없었기 때문에 φ 는 0이된다.. 따라서 식 (9)를 식 (6)에 대입하면 식 (10)을 구할 수 있다.

$$ {\mathrm{\theta }}_2={\mathit{cos}}^{-1}\left(\frac{x-l_1}{l_2}\right)$$

(10)

위 식을 이용하여 end-effector를 원하는 위치로 이동시킬 수 있다.

3. 시스템 구성 및 실험

위의 테이블을 이용하여 행렬을 구할 수 있다. 그 결과를 이용하여 MSRDS 3D Simulation을 이용해 수식의 적합성을 먼저 검증하였다. 2대의 로봇을 이용하여 물체를 양 쪽에서 협조하여 들어올리는 동작을 앞에서 구한 역기구학 식들을 이용하여 Simulation하였다. 시뮬레이션 결과 모바일 로봇의 거리가 안정적으로 감소하면서 머니퓰레이터가 움직이는 것을 Fig. 9를 통해 확인할 수 있었다. 이것을 이용하여 3대로 확장하여 연구를 진행하였다.

Figure. 9.

3D simulation result

모바일 로봇은 다음과 같이 Fig. 10의 임베디드 컴퓨터와 ARM, 모터드라이버, Wi-Fi 모듈을 이용하여 Fig. 11과 같이 회로를 구성하였다. 임베디드 컴퓨터 자체에서 RS485통신 을 통해 Dynamixel 이라는 서보모터와 통신하여 머니퓰레이터를 제어 할 수 있다.

Figure. 10.

Hardware of the mobile robot

Figure. 11.

System configuration

각 로봇은 Embedded Computer가 제어한다. 처음에는 Embedded Computer에서 Encoder값을 바로 받아왔으나 Encoder값 인식 속도차이로 ARM에서 Encoder 값을 받아오도록 하였다. 로봇의 Embedded Computer는 각각 다른 로봇의 Embedded Computer와 Wi-Fi 통신으로 연결 되어있다.

Fig. 12와 같이 로봇과 운반할 물체를 배치하고 협조제어 시스템을 시험하였다. 삼각형의 물체를 두고 3대의 로봇이 특정 위치에서 물체를 잡을 목적지까지 주행 한 후 머니퓰레이터를 이용해 물체를 들어올린다. 물체를 들어올린 후 한 방향으로 직선 주행을 하도록 실험을 하였다.

Figure. 12.

Configuration environment for cooperative control.

각 로봇이 물체를 향해 접근 한 후 물체를 들어 올린 후 한 방향으로 직선 주행하는 것을 좌표로 나타내었다. 로봇들이 물체를 향해 각각 (0,0), (55,0), (30,250)에서 출발하여 (10,100), (45,100), (30,150)으로 이동하여 물체를 들어 올린 후, 전체 로봇이 y축 방향으로 30cm 정도 이동한 결과이다. Encoder 값에 PD제어기를 사용함으로써 비교적 주행 제어가 잘 되는 것을 Fig. 13에서 확인 할 수 있다.

Figure. 13.

Driving result of mobile robot

Fig. 14 및 15와 같이 실제 실험에서 세 대의 로봇들이 함께 물체를 파지하고 운송하는 것을 볼 수 있다.Fig .15

Figure. 14.

Result of experiment (before)

Figure. 15.

Result of experiment (after)

4. 결 론

본 논문은 역기구학 해석을 사용하여 다수 로봇의 협조제어 시스템에 대한 연구이다. 협조 제어나 군집 제어는 대부분의 연구가 이론과 시뮬레이션을 통한 연구에 그치고 있어 그 알고리즘의 실효성을 보지지 못하고 있으므로, 본 논문에서는 실제 다수로봇이 협동적으로 하나의 물체를 운반하기 위한 전체적인 시스템을 구성하여 Master-slave 모드로 협조하면서 하나의 물체를 이동할 수 있음을 보였다. Encoder와 Kinematics에 기반하여 모바일 로봇의 위치를 구하고, 목표 위치로 협동적으로 움직이게 하였으며, 들어올리는 동작과 내려놓는 동작을 이동로봇의 상부에 부착된 머니퓰레이터의 협조 제어로 수행할 수 있음을 보였다. 본 연구를 통하여 물체의 무게에 따라 협조제어 시 오차가 달라지는 것을 확인 할 수 있었으며, 향후 힘 제어 기법을 이용하여 무게와 외부 환경에도 강인한 제어 성능을 가질 수 있도록 설계 할 계획이다. 또한 향후 머니퓰레이터 상단에 부착된 카메라를 이용하여 전체적인 시스템을 완성할 것이며, 로봇 간의 통신을 구현하여 좀 더 정밀하고 효율적으로 물체를 협동적으로 운반하고 조립하는 시스템을 연구할 계획이다.

References

• Tak, MH, Cho, YJ, Joo, YH, "Behavior Control for Cooperative Exploration for Swarm Robots", Proceedings of KIIS Fall Conference, Korea, (2011, Dec), 21(2), p169-170.
• Jung, WG, Choi, YS, Seo, HC, Lee, SG, Lee, DH, "A Study on Cooperative Behaviors of Multiple Autonomous Robots", Proceedings of KIEE Summer Conference, Korea, (1999), p3030-3032.
• Lee, IJ, Baek, SM, Son, KO, Guk, TY, "Behavior Synchronization Control Algorithm for Swarm Robot", Proceedings of the 13th KACC, Korea, (1998, Oct), p252-255.
• Lee, DW, Sim, KB, "Study on Cooperative Behaviors and Cooperative Control in Collective Autonomous Mobile Robots", Proceedings of Institute of Electronics and Information Engineers Conference, Korea, (1997, Jan), p68-71.
• Kim, HC, Kim, JS, Ji, YK, Park, JH, "Path Planning of Swarm Mobile Robots Using Firefly Algorithm", Journal of Institute of Control. Robotics and Systems, (2013, May), 19(5), p435-441. [https://doi.org/10.5302/j.icros.2013.13.9008]
• Kim, JS, Yeom, DH, Joo, YH, Park, JB, "Hierarchical Control of Multiple Mobile Robots", Proceedings of KIEE Summer Conference. Pyeongchang-gun, Korea, (2011, Jul), p1890-1891.
• Park, BS, “Leader-Follower Based Formation Control of Multiple Mobile Robots Using the Measurements of the Follower Robot”, Journal of Institute of Control. Robotics and Systems, (2013), 19(5), p385-389. [https://doi.org/10.5302/j.icros.2013.13.9001]
• Oh, YS, Park, JH, Kim, JH, Huh, UY, “Obstacle Avoidance of Leader-Follower Formation, Trans. KIEE, (2011), 60(9), p856-861. [https://doi.org/10.5370/kiee.2011.60.9.1761]
• Lee, KT, Jung, CB, Jung, DU, Chung, WJ, “Accurate Calibration of Kinematic Parameters for Two Wheel Differential Drive Robots by Considering the Coupled Effect of Error Sources”, Journal of Korea Robotics Society, (2014), 9(1), p39-47. [https://doi.org/10.7746/jkros.2014.9.1.039]
• Jung, CB, Moon, CB, Jung, DU, Chung, WJ, “Design of Experimental Test Tracks for Odometry Calibration of Wheeled Mobile Robots”, Journal of Korea Robotics Society, (2014), 9(3), p160-169. [https://doi.org/10.7746/jkros.2014.9.3.160]
• Choi, HS, “A Study on the Control of Tow-Cooperating Robot Manipulators for Fixtureless Asscembly”, Trans. Korean Soc. Mech. Eng. (A), (1997), 21(8), p1209-1217.