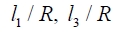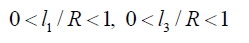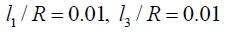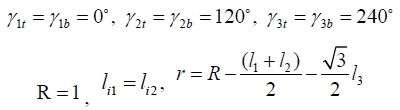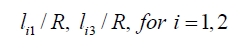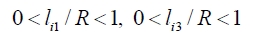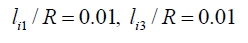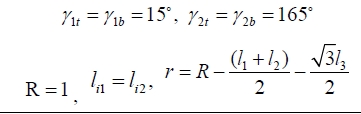회전관절만을 활용하는 병진 3자유도 병렬 메커니즘의 기구학 특성 분석

2.1. 메커니즘 구조

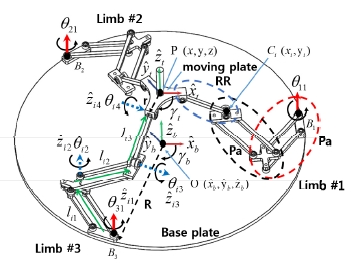
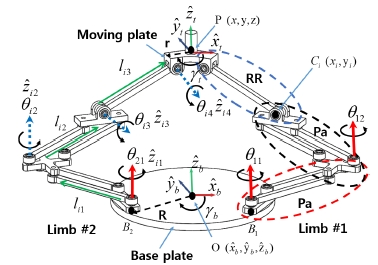
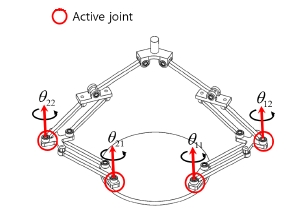
Fig. 1과 같이 3 −P_aP_aRR 형 메커니즘은 고정판과 운동 판 그리고 이들을 연결하는 3개의 P_aP_aRR 형 부속체인으 로 구성된다. 각 부속체인은 고정판과 운동판에 대칭성을 유지하도록 배치되어 있으며 평행사변형 모듈( P_a ) 2개와 회전 관절( R ) 2개로 이루어져 있다. 평행사변형 모듈은 4 개의 링크와 4개의 회전 관절로 이루어지며 각 모든 회전 관절 축은 모두 고정판에 수직인 방향을 가진다 ( zˆi1zˆi2zˆ for i = 1,2,3 ). 여기서 ""•ˆ" "는 단위 벡터를 나타 낸다. 나머지 두 개의 회전관절 축은 고정판에 평행한 방 향으로 서로 평행하다( zˆi3zˆi4 for i= 1,2,3). 3 −P_aP_aRR 형 메커니즘의 구동 관절은 고정판에 고정된 첫 번째 관 절들 θ_a = (θ₁₁,θ₂₁,θ₃₁) ^T 로 설정하여 모든 엑츄에이터를 모 두지면에 배치하였다.

Fig. 1.

3 −PaPaRR type PM

메커니즘의 기저 좌표계 xˆb,yˆb,zˆb 와 출력 좌표계 xˆt,yˆt,zˆt 는 각각 고정판과 운동판의 중앙에 위치한다. 각 부속체인의 첫 번째 관절은 고정판의 중심에 위치한 반경 R 인 원상에 xˆb 축으로부터 오프셋 각 γ _ib 의 위치에 고정 되며, 운동판에 연결되는 회전관절은 운동판의 반경 r 인 원상에 xˆt 축으로부터 오프셋 각 γ _it 의 위치에 고정된다. θ _ij 와 l→ij 는 각각 i 번째 부속체인의 j 번째 회전 관절각 및 링크를 의미 한다.

2.2. 모빌리티 분석

본 논문에서 제시된 3 −P_aP_aRR 형 병렬 메커니즘과 같 이 모든 부속체인이 동일한 하나의 공통 운동판을 가지는 병렬 메커니즘에 대한 모빌리티(M)는 다음과 같은 Modified Grübler − Kutzbach 의 공식을 활용하여 구할 수 있다^[8]:

여기서 d(= 6 −λ )는 메커니즘의 모든 관절 스크류(screw) 를 포함하는 스크류 시스템의 차원수, n 는 링크의 수, g 는 지면을 포함한 관절의 수, f_i 는 관절의 자유도, 그리고 υ 와 λ 는 각각 모든 부속체인에 의해 운동판에 가해지는 독립적인 과다구속렌치(redundant constraints wrench) 수와 독 립적인 공통구속렌치(common constraints wrench) 수를 나타 낸다.

다음은 운동판의 중앙에 고정된 기준(출력) 좌표계에 대 한 각 부속체인의 모든 관절 스크류를 나타낸다.

여기서 zˆi3 다음과 같으며

(2)와 (3)에서와 같이 평행사변형 모듈은 원호를 따라 선형 운동을 가지되 방위각은 변화하지 않는 일반화된 관절 (generalized kinematic pairs)로 표현되었다^[9].

한편, 각 부속체인의 모든 관절 스크류 (2)~(5)에 대한 reciprocal screw (즉, 메커니즘의 운동판에 가해지는 구속렌 치)는 다음과 같이 구해진다.

(7)로부터 모든 부속체인에 의해 공통으로 메커니즘의 운 동판에 가해지는 공통 구속렌치는 z 축 방향의 infinitepitch wrench(토크) $ˆi1r 한 개임(λ = 1 )을 알 수 있다. 따라 서, 각 부속체인에 속한 관절들의 허용 운동공간 차원수는 전체 운동공간에서 공통 구속렌치 차원 수를 제외함으로 써 즉, d = 6 − λ 와 같이 5임이 확인된다. 그리고 (7)에서 공통구속렌치를 제외한 나머지 구속렌치는 모두 동일 평 면상의 infinite-pitch wrench(토크)이므로 결과적으로 독립적 인 구속렌치는 두 개이며 따라서 한 개의 과다구속렌치가 존재함을 확인할 수 있다 (υ = 1).

이상의 결과를 (1)에 대입 함으로서 메커니즘의 자유도 는 다음과 같이 3임이 확인된다:

여기서 총 링크 수는 운동판과 고정판 그리고 각 부속체 인 링크 3개로 총 11개이며 총 관절 수는 각 부속체인에 4 개씩 총 12개로서 모든 관절이 1자유도를 가진다. 특히, 평 행사변형 모듈의 경우 한 개의 가상링크와 하나의 가상 미끄럼 관절로 단순화된 관절모델로 사용하였다.

2.3 역위치 해석

역위치 해석에서는 출력 변수 위치벡터 u = (x y z) ^T 가 주어졌을 경우 구동 관절의 변수 벡터 θ_a = (θ₁₁,θ₂₁,θ₃₁) ^T 를 구한다. 본 논문에서 소개하는 3 −P_aP_aRR 형 메커니즘의 오프셋 각 γ _bi 와 γ _ti 는 각 부 속체인이 고정판과 운동판 사이에 대칭으로 배치되도록 아래와 같은 값을 갖도록 설정하였다.

3 −P_aP_aRR 형 병렬 메커니즘의 역위치 해석은 두 단계 로 이루어진다. 첫 번째 단계에서는 주어진 출력 위치벡터 값으로부터 각 부속 체인의 세 번째 관절 값( θ _i3 )을 구한 후 이로부터 세 번째 관절의 위치 x_i y_i^T ( i = 1,2,3 )를 산출한다. 두 번째 단계에서는 x_i y_i^T 을 이용하여 첫 번째 관절각( θ _i1 )을 구한 후, 이를 이용하여 두 번째 관절 각( θ _i2 )을 구하는 순서로 이루어진다.

2.4. 정위치 해석

정위치 해석에서는 구동 관절 변수 벡터 θ_a = (θ₁₁,θ₂₁,θ₃₁) ^T 가 주어졌을 경우 출력 변수 위치벡터 u = (x y z) ^T 를 구한다. 각 부속체인에 대하여 얻어진 (19)는 입력변수벡터와 출력 위치 벡터와의 관계식을 나타 내며 이 식을 이용하여 정위치 해석을 수행할 수 있다. 하 지만, 3 −P_aP_aRR 형 메커니즘의 정위치 해석해는 존재하 지 않으므로 Newton-Raphson기법과 같은 수치 해법을 통 하여 계산할 수 있다.

2.5. 일차 기구학 모델

본 논문에서는 스크류 이론을 이용하여 얻어진 일차 기 구학 모델에 관하여 기술한다. (2)~(5)에 주어진 부속체인의 관절 스크류 중에서 구동관절 스크류를 제외한 나머지 관 절 스크류에 reciprocal 한 렌치는 구동관절에 의해 운동판 에 가해지는 구동렌치를 의미하며 다음과 같이 구해진다. 먼저, reciprocal 렌치 $ˆi1r 가 다음과 같은 형태를 가진다고 할 때,

다음의 reciprocal 스크류 조건들로부터

구하고자 하는 reciprocal 렌치 $ˆi1r 는 다음과 같이 얻어진다.

여기서

메커니즘의 운동판에 고정된 기준 좌표계의 운동 스크류 ($ _p )는 각 부속체인의 관절에 의해 다음과 같이 표현된다.

(32)의 양변에 각 부속체인의 구동관절에 의해 운동판 에 가해지는 렌치 $ _i1^r 와의 orthogonal product operation 를 아 래와 같이 적용한다.

(33)을 행렬식으로 정리하면 다음과 같이 메커니즘에 대 한 일차 기구학 모델이 얻어진다^[10]:

A의 역행렬이 존재하는 경우, (34)로부터 정속도 관계식은 다음과 같이 얻어진다.

2.6. 병렬 특이형상

3 −P_aP_aRR 메커니즘의 병렬 특이형상은 (36)의 행렬 A 의 행($ˆi1r , for 1,2,3), 즉, 구동관절에 의해 운동판에 가 해지는 구동렌치를 나타내는 reciprocal 렌치들이 메커니즘 의 출력공간인 병진 3자유도 공간(translational 3-DOF space) 내에서 서로 종속적인가를 확인함으로써 규명할 수 있다. 특히, 본 메커니즘의 경우 구동렌치 및 구속렌치가 모두 zero-pitch렌치 또는 infinite-pitch 렌치의 형태로서 모두 선 으로 나타낼 수 있다. 따라서, GLG(Grassmann Line Geometry)기법을 사용하여 이들 선들의 종속성을 분석함 으로써 특이형상을 규명한다.

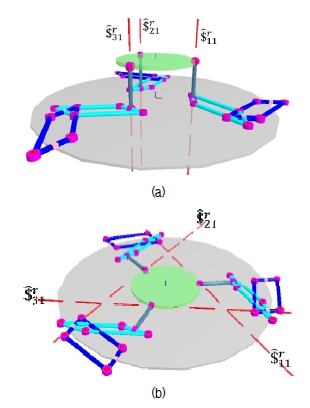
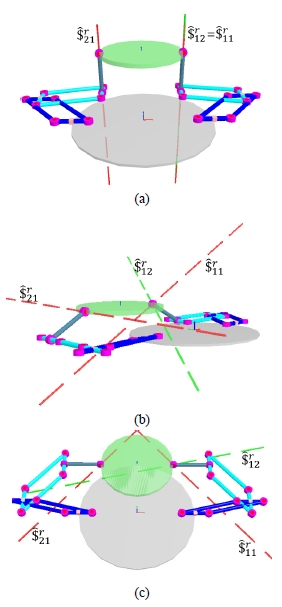
Fig. 2(a)와 Fig. 2(b)는 각각 3 −P_aP_aRR 형 메커니즘이 가 지고 있는 병렬 특이형상이다. Fig. 2(a)의 경우 세 개의 구 동렌치 축(선)이 모두 고정판에 수직한 경우를 나타낸다. 이러한 형상에서는 세 개의 구동관절에 의해 운동판에 가 해지는 구동렌치는 모두 고정판에 수직한 방향( z 축 방향) 으로의 힘만을 제공할 수 있으므로 x − y 평면에 놓인 임 의 축 방향으로의 구동토크는 메커니즘에 가해진 구속렌 치에 의해 발휘되지 못하며, 단지 z 축 방향으로의 힘만을 제공할 수 있다. 따라서, 메커니즘의 병진 3자유도 출력공 간 중 나머지 두 개의 방향으로는 힘을 제공하지 못한다.

Fig. 2(b)의 경우 세 개의 구동렌치 축(선)이 모두 고정판 에 평행한 경우를 나타낸다. 이러한 형상에서는 구동관절 에 의해 가해지는 구동렌치는 x − y 평면 위의 힘 만을 전 달할 수 있으므로, z 축 방향의 힘을 제공하지 못한다.

Fig. 2.

Singularity configurations of the 3-PaPaRRtype PM

2.7. 최적설계

병렬 메커니즘이 대칭구조를 가지므로 각 부속체인의 링크길이는 같다고 가정한다: 즉, l₁ = l_i1, l₂ = l_i2, l₃ = l_i3 그리고 l₃ = l_i3 ( i = 1,2,3 ). 따라서, 기구학 설계인자로서는 R, r, l₁, l₂ 그리고 l₃ 인 총 다섯 개의 인자를 고려해야 하 지만 설계를 단순화하기 위하여 다음과 같이 두 개의 구 속조건을 추가하였다: 즉, l₁ = l₂ 그리고 R=r+l1+l22+32l3. 특히 두 번째 구속조건은 운동판 의 위치가 (0,0, l₃/ 2) 일 때 즉, 작업공간의 중앙에 있을 때, 운동판의 중앙점에서 각 부속체인의 첫 번째 관절의 위치벡터 방향으로 투영된 해당 부속체인에 포함된 두 평 행사변형 링크의 길이가 (l₁ + l₂) / 2 인 값을 가지도록 하 는 조건으로 작업공간의 크기를 효과적으로 최대화하기 위한 목적이었다. 나머지 세 개의 설계 변수에 대해서는 R 에 대해 정규화 함으로써( R = 1 ) 최종적으로 l₁ / R 과 l₃ / R인 두 개의 설계변수로 축소한 후 이들 각각 정규화 된 인자들의 값의 범위(즉, 0 부터 0.5 까지의 범위)내에 서 최적설계를 수행하였다. Table 1은 설계인자, 검색범위, 최적설계 검색시 설계인자 분해능, 그리고 추가로 부여된 설계구속조건의 요약이며 Table 2는 작업공간 검색에서 설 정된 격자크기 및 작업공간 검색범위를 나타낸다.

Table 1.

Design parameters and design constraints

Table 2.

Search conditions in workspace simulation

최적 설계 지수로는 전역 기구학 등방성 지수(global kinematic isotropy index) σ _GI 와 작업공간 크기 W 를 활용 하였다. σ _GI 는 다음과 같이 정의된다:

여기서 σ _min 과 σ _max 는 각각 자코비안 행렬의 특이값 (singular value)의 최소와 최대 값을 나타내며, σ _min/ σ _max 값은 해당 형상에서의 지역 기구학 등방성 지수를 나타낸 다. 그리고 작업공간 크기 W 는 일반적으로 모든 도달 가 능한 공간을 활용하지만 편이상 특히 본 시뮬레이션에서 는 병렬 특이형상을 포함하지 않으면서 메커니즘의 중앙 에 위치한 영역만을 작업공간으로 설정하였다. 이러한 작 업공간의 경계는 병렬 특이형상이나 직렬 특이형상의 형 태로 나타내며 시뮬레이션에서는 자코비안 행렬의 디터미 넌트 (determinant) 값의 부호가 바뀌는 경계로 확인할 수 있다.

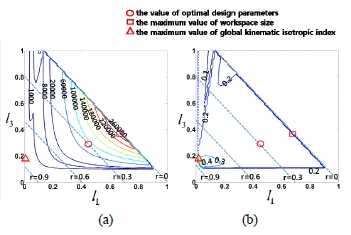
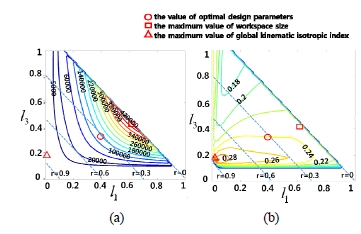
Fig. 3(a)와 Fig. 3(b)는 각각 정규화된(즉, 설계인자들의 기 준 값인 고정판의 반경을 단위 값으로 설정한 경우) 두 설 계인자 l₁ / R 과 l₃ / R들에 대한 메커니즘의 전역 기구학 등방성 지수 등고선도와 작업공간의 크기를 나타낸다. 이 시뮬레이션에서 작업공간의 크기는 작업공간 내 정의된 격자 형태의 교차점(node)의 수로 산출하였으며 전역 기구 학 특성을 분석하기 위한 시뮬레이션에서는 작업공간 내 에 정의된 모든 격자 교차점에서의 지역 등방성 기구학 지수 값들의 평균치로 산출하였다. 구체적으로 작업공간 내 x 축, y 축 그리고 z 축 각 방향으로의 각 설계인자들 에 대한 간격은 0.01 × R 인 값으로 사용하였으며 따라서 각 격자 셀의 크기는 공통적으로 (0.01 × R)³인 크기를 갖 는다.

Fig. 3.

(a) Global kinematic isotropy index plot and (b) workspace size

이들 결과로부터 원하는 메커니즘의 작업공간의 크기와 기구학 등방성 지수 특성을 고려하여 메커니즘의 최적 설 계인자를 설정하였다. Fig. 3에 표시된 기호 와 기호 는 각각 최대 전역 등방성 지수와 최대 작업공간 크기를 나 타낸다. 그림으로부터 l₁ / R 과 l₃ / R 가 클수록 작업공간 의 크기는 커지는 경향이 있는 반면 적을수록 전역 등방 성 지수 특성이 좋아지는 경향이 있음을 알 수 있다. 한편, Fig. 3에서 점선으로 표기된 사선은 운동판의 반경 값을 나 타낸다. 실제 메커니즘의 구현 시 운동판의 반경이 작을 경우 부속체인을 연결하는 회전관절의 설치가 어려운 점 을 고려하여 r = 0.3 R 이며 기호 와 기호 를 연결하는 선상에 있는 기호 의 위치에 해당하는 인자 값들을 최적 설계인자로서 선정하였으며 그 값은 각각 다음과 같다:

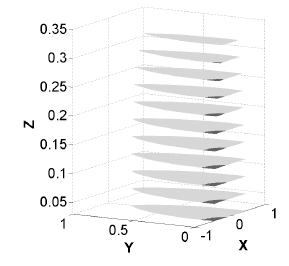
Fig. 4와 Fig. 5의 경우는 선정된 최적인자들의 값 r = 0.3 , l₁ = l₂ = 0.45 그리고 l₃ = 0.3에 해당하는 메커니 즘에 대한 x − y 평면상에서의 기구학 등방성 지수 등고선 도와 메커니즘의 전체 작업공간을 나타낸다. Fig. 4와 Fig. 5 에서 x, y, z 각 축의 단위는 모두 R = 1인 기준 값에 대 해 정규화하였다. Fig. 4에서 바깥 경계 부근에 나타나는 흰 색 영역은 기구학 등방성 지수 값이 매우 낮은 영역으로 서 그 중앙부근에는 특이형상이 존재한다. 이러한 사실은 Fig. 5에서 재확인될 수 있다. Fig. 5에서는 도달 가능한 작 업공간을 자코비안의 디터미넌트 값의 부호에 따라 회색 영역과 검은색 영역으로 표기하였으며 따라서, 특이형상 궤적은 회색 영역과 검은색 영역의 경계에 해당된다. 이러 한 결과로부터 본 메커니즘은 작업공간의 크기와 작업공 간의 중앙부근에서 우수한 기구학 등방성 특성, 그리고 작 업공간의 중심으로부터 경계부근까지 비교적 완만하게 감 소하는 추세를 나타내는 전반적인 기구학 등방성 특성을 고려할 때 햅틱기기로 활용하기에 매우 적합함을 확인할 수 있다.

Fig. 4.

Kinematic isotropy index plots

Fig. 5.

Workspace plot

3.1. 메커니즘 구조 및 모빌리티 분석

2 −P_aP_aRR형 메커니즘은 Fig. 6과 같이 고정판과 운동 판 그리고 이들 두 개의 판을 연결하는 2개의 부속체인으 로 구성되어 있다. 각 부속체인은 3 −P_aP_aRR 형 부속 체 인과 동일한 구조를 가진다. 따라서, 제시된 2 −P_aP_aRR형 병렬 메커니즘의 자유도는 3 −P_aP_aRR 형 병렬 메커니즘과 유사한 방법으로 다음과 같이 얻어진다.

Fig. 6.

A 2 −PaPaRR type PM

각 부속체인의 관절 스크류는 (2)~(6)과 유사하게 표현되 며 이들 모든 관절 스크류에 대한 reciprocal 스크류(부속체 인에 의해 운동판에 가해지는 구속렌치) 또한 (8)과 유사 한 형태로 표현된다. 그러나, 2 −P_aP_aRR형 병렬 메커니즘 의 경우 부속체인이 두 개이므로 공통구속렌치는 하나로 동일하지만 나머지 두 개의 구속렌치가 모두 독립적인 렌 치이므로 과다구속렌치는 존재하지 않는다. 즉, λ = 1, d = 6 − λ = 5, 그리고 υ = 0.

한편, 3 −P_aP_aRR 형 병렬 메커니즘과 마찬가지로 2 −P_aP_aRR형 메커니즘의 단순화된 관절모델에 대한 링크 수는 총 8개이고 관절은 모두 1자유도로서 총 8개로 표현 된다. 따라서, Modified Grübler − Kutzbach 공식으로부 터^[8] 2 −P_aP_aRR 형 메커니즘의 모빌리티는 다음과 같이 3자유도를 갖는다.

그러나, 두 부속체인간의 오프셑 각의 차이가 γ_2t - γ_1t = 180° 인 경우 공통 구속렌치(λ )는 2개를 가지므 로 메커니즘의 자유도는 다음과 같이 4자유도를 갖는다:

본 논문에서는 3자유도를 가지는 경우로 한정하여 γ_2t - γ_1t = 180° 인 메커니즘에 대한 해석은 제외하였다.

3.2. 정위치 해석

제시된 2 −P_aP_aRR 형 메커니즘이 비여유 구동이 되는 경우는 모빌리티 분석결과에서 알 수 있는 바와 같이 세 개의 구동관절이 요구되며 그 위치로서는 첫 번째 부속체 인의 첫 번째와 두 번째 관절, 그리고 두 번째 부속 체인 의 첫 번째 관절을 설정하였다 (θ_a = (θ₁₁,θ₁₂,θ₂₁) ^T). 따라 서, 본 절에서의 정위치 해석에서는 설정된 구동 관절의 변수 벡터 θ_a = (θ₁₁,θ₁₂,θ₂₁) ^T 가 주어졌을 경우 출력 변수 위치벡터 u = (x y z) ^T 를 구한다.

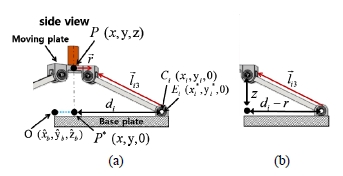
Fig. 7은 2 −P_aP_aRR 형 메커니즘의 측면도를 보여준다. 출력점 P가 고정판에 투영된 점을 P* , 부속체인의 세 번 째 관절의 위치를 C_i ( x_i, y_i, 0) , 그리고 부속체인의 두 번 째 관절의 위치를 E_i ( x_i*, y_i*, 0) 로 각각 정의하였다. 여기 서 C _i 와 E _i 는 동일한 점에 위치 한다, 그리고 P*와 C _i 의 거리를 d _i 로 정의 하였으며 d ₁ 과 d ₂ 의 거리는 같다.

Fig. 7.

Side view of the upper plate and the link li3 of the 2 −PaPaRR type PM

첫 번째 부속체인에 관련 위치벡터 OC1→와P∗C1→ 는 각 각 다음과 같이 표현된다:

한편, 두 번째 부속체인의 OE2→와P∗E2→ 는 각각 다음과 같이 표현된다:

(45)와 (46)을 이용하면 P∗C1→와P∗E2→ 에 대한 루프 방 정식이 아래와 같이 얻어진다:

(48)를 각각 제곱하여 더한 후 d ₁ 에 관하여 정리하면 다음 과 같다.

여기서

(49)로부터 d ₁ 는 다음과 같이 얻어 진다.

한편, Fig. 7(b)으로부터 세 번째 관절과 운동판의 기하 관 계로부터 d ₁ 는 다음과 같이 얻어진다:

(45)와 (54)로부터 운동판의 위치인 출력 벡터 u = (x y z) ^T 는 다음과 같이 표현된다.

3.3. 역위치 해석

2 −P_aP_aRR 메커니즘의 역위치 해석은 3 −P_aP_aRR 메커 니즘의 역위치 해석과 유사한 방법으로 구할 수 있으며 본 논문에서는 생략한다.

3.4. 일차 기구학 모델

2 −P_aP_aRR 형 병렬 메커니즘의 기구학 모델의 경우도 3 −P_aP_aRR 형 병렬 메커니즘의 경우와 유사하므로 그 과 정은 생략한다. 최종적인 일차 기구학 모델은 다음과 같이 표현된다.

여기서

A의 역행렬이 존재하는 경우, (56)으로부터 정속도 관계식 은 다음과 같이 얻어진다.

3.5. 병렬특이형상

2 −P_aP_aRR형 메커니즘의 병렬 특이형상은 (58)의 행렬 A 의 행들인 reciprocal 렌치 $ˆi1r,$ˆ12r , 그리고 $ˆ21r 들이 서로 종속하는 가를 확인함으로써 규명할 수 있다. Fig. 8은 병렬 특이형상을 나타내며 Fig. (a)는 모든 {$ˆi1r,$ˆ12r for i = 1,2 } 가 평행한 경우, Fig. 8(b)는 $ˆ11r와$ˆ12r 축이 놓인 평면에 $ˆ21r 축이 평행할 경우, 그리고 Fig. (c)는 $ˆ11r축,$ˆ12r 축, 그 리고 $ˆ21r 축이 모두 한 평면에 위치하는 경우이다.

Fig. 8.

Parallel singularities of the 2 −PaPaRR type PM

3.6. 최적설계

2 −P_aP_aRR 형 메커니즘의 설계인자와 구속조건은 3 −P_aP_aRR 형 메커니즘과 동일하며 평가지수의 경우도 3 −P_aP_aRR 형 메커니즘에서 사용된 성능지수와 동일한 전 역 등방성 등방성 지수( σ _GI )와 작업공간 크기(W )로 활용 하였다.

최적 설계 인자를 선정하기 위해 일차적으로 운동판 과 고정판의 오프셑 각 γ _it 와 γ _ib 의 최적 값을 먼저 선정하 였다. 이를 위해 고정판 반지름을 단위 값으로 ( R = 1 ) 정 규화하여 운동판 반지름은 r = 0.35로, 그리고 모든 링크 길이는 l₁ = l₂ = l₃ = 0.35로 고정하였으며, 두 다리와 운동 판의 오프셑 각의 차(γ_2t - γ_1t)에 대한 최적의 각을 검색 하였다. 편의상 γ_2t = γ_2b 그리고 γ_1t = γ_1b 로 설정하였으 며, 앞에서 언급한 바와 같이 메커니즘의 자유도가 4가 되 는 운동판과 고정판의 오프셑 각들이 각각 0° 와 180° 인 경우는 배제하였다. 검색 결과 운동판과 고정판에 대한 최 적의 오프셑 각의 차는 150° 로 선정되었으며, 이에 따라 γ _it 와 γ _ib 는 각각 대칭구조를 이루는 15° 와 165° 로 설 정하였다. Fig. 9(a)는 이러한 최적인자 값을 활용한 메커니 즘의 작업공간을 나타내며 Fig. 9(b)는 특히 z = 0.25 일 때에 대한 기구학 등방성 지수 등고선도를 나타낸다.

Fig. 9.

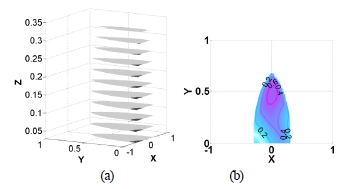
(a) Workspace plot and (b) kinematic isotropy index plot, with respect to optimal offset angles of the upper plate and the base plate

Table 3와 Table 4는 각각 앞에서와 마찬가지로 최적설계 를 수행하는데 적용한 조건을 나타낸다. 그리고 최적설계 는 3 − P_aP_aRR 형 메커니즘과 동일한 방법으로 수행하였다.

Fig. 10.

(a) Global kinematic isotropy index plot and (b) workspace size.

Table 3.

Design parameters and design constraints

Table 4.

Search conditions in workspace simulation

Fig. 10(a)와 Fig. 10(b)는 각각 정규화된 설계인자들에 대 한 메커니즘의 전역 기구학 등방성 지수 등고선도와 작업 공간의 크기를 나타내며, 특히, 이들 그림에 표시된 기호 와 기호 는 각각 최대 전역 기구학 등방성 지수와 최대 작업공간 크기를 나타낸다. 그리고 기호 는 Fig. 3에서와 동일한 방법으로 기호 와 기호 를 연결하는 선상에 있 는 값들 중에서 전역 등방성 지수와 작업공간크기 그리고 제작의 용이성을 고려하여 임의로 선정된 최적 설계인자 의 위치를 나타내며 그 값은 다음과 같다.

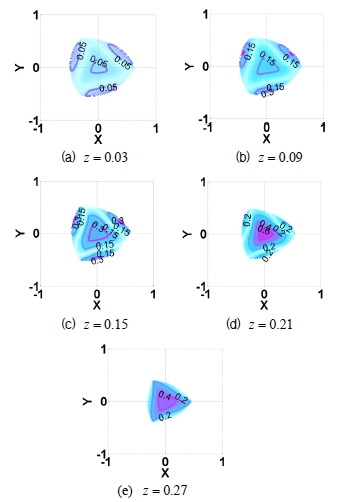
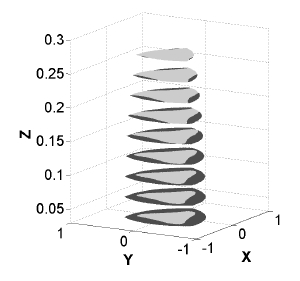
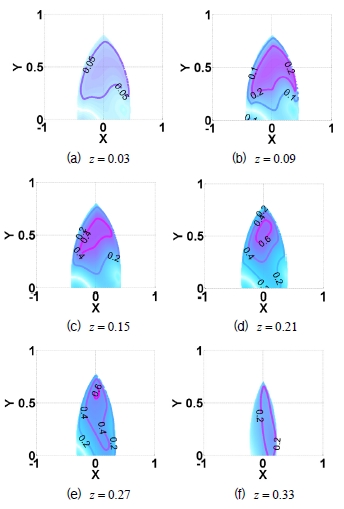
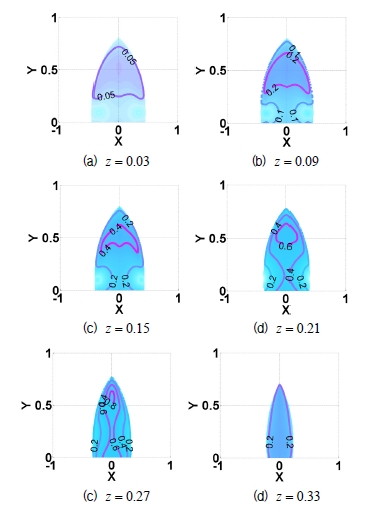
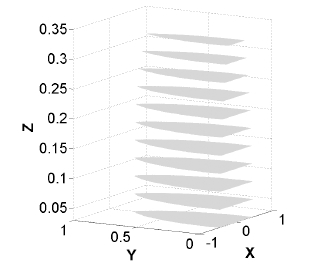
Fig. 11과 Fig. 12는 각각 고정판이 R = 1일 때, 최적 인자 들의 실제 값이 각각 r = 0.3, l₁ = l₂ = 0.4 그리고 l₃ = 0.35일 때 메커니즘의 작업공간과 기구학 등방성 지 수 등고선도이다. 앞에서 설정한 최적 설계인자를 가지는 병렬 메커니즘에 대해 z = 0.03, 0.09, 0.15, , 0.21 , 0.27 , 그리고 0.33인 경우 각각 x − y 평면상에서의 기구학 등 방성지수 등고선도를 나타낸다. 기구학 특성 분석을 위해 σ _I = σ _min /σ _max 로 정의되는 지역 기구학 등방성 지수 (σ _I )가 사용되었다. 여기서 σ _min 와 σ _max 는 각각 (63)에 서 구한 자코비안 행렬의 최소 특이값과 최대 특이값을 나타낸다. 특히, Fig. 12에서 등방성 지수의 문턱 값으로는 σ _th = 0.01 를 사용하였으며 이러한 문턱 값은 그림에서의 작업공간 경계를 나타낸다.

Fig. 11.

Workspace of the optimal 2 −PaPaRR type PM

Fig. 12.

Kinematic isotropy index plot of the optimal 2 −PaPaRR type PM

그림에서 얻어진 작업공간 크기 및 기구학 등방성 특성 으로부터 메커니즘이 어느 정도 유용한 기구학 특성을 가 지고 있는 것으로 판단할 수 있다. 하지만 Fig. 11에서 검은 색 부분 또는 Fig. 12에서 흰색으로 나타나는 좌측 하단 부 분은 메커니즘의 병렬 특이형상으로서 작업공간의 한 부 분의 유용성을 급격히 저하시키고 있음을 확인할 수 있다. 따라서, 이와 같은 작업공간 내부에 존재하는 병렬 특이형 상을 제거하기 위한 방안으로서 다음절에서는 여유구동을 활용하는 경우에 대한 특이형상 및 기구학 특성 분석을 수행함으로써 더 넓은 작업공간을 확보할 수 있음을 조사 하였다.

3.7. 여유구동으로 인한 병렬 특이형상 제거

Fig. 13은 각 부속체인의 첫 번째와 두 번째 관절을 구동 관절로 설정하여 총 4개의 구동관절을 가지는 여유구동 2 −P_aP_aRR 메커니즘을 나타낸다. 이러한 여유구동 메커 니즘의 일차 기구학 모델은 B_r 의 역행렬이 존재한다면 다음과 같이 얻어진다:

Fig. 13.

Redundantly actuated 2 −PaPaRR type PM

여기서

정속도 관계식은 (65)로부터 다음과 같이 얻어질 수 있 다

여기서 [J ^-1_r]⁺ 는 유사역행렬(pseudo-inverse matrix)로서 다 음과 같이 표현된다:

Fig. 14와 Fig. 15는 각각 3.6절에서와 동일한 설계인자 를 가지는 병렬 메커니즘에 대해 z = 0.03, 0.09, 0.15, 0.21, 0.27, 그리고 0.33인 경우 각각 x − y 평면상에서의 기구학 등방성지수 등고선도와 전체 작업공간의 크기를 나타낸다. 지역 기구학 등방성 지수에 사용된 특이값 σ _min와 σ _max 는 각각 (72)에 나타난 유사 역행렬([J ^-1_r]⁺ )의 최소 특이값 과 최대 특이값을 나타낸다. Fig. 14와 Fig. 15에서 등방성 지수의 문턱 값으로는 σ _th = 0.01 를 사용하였으며 이러한 문턱 값은 그림에서의 작업공간 경계를 나타낸다.

Fig. 14.

Kinematic isotropy index contour plot of the redundantly actuated 2 −PaPaRR type PM

Fig. 12와 Fig. 13에서와 같이 여유구동이 없는 2 −P_aP_aRR 형 메커니즘의 작업공간 좌측 하단에는 병렬 특이형상이 존재하지만 하나의 여유 구동을 가지는 2 −P_aP_aRR형 메커니즘의 경우에는 Fig. 15와 같이 작업공 간 내에서는 특이형상이 완전히 제거되어 넓은 유용한 작 업공간을 확보할 수 있을 뿐 아니라 기구학 등방성 특성 이 향상된 것을 확인할 수 있다.

Fig. 15.

Workspace plot of the redundantly actuated 2 −PaPaRR type PM