저가형 LIDAR를 장착한 소형 무인항공기의 3차원 실내 항법 및 자동비행
†Corresponding author: Dept. of Aerospace Engineering, Korea Advanced Institute of Science and Technology, 291 Daehak-ro, Yuseong-gu, Daejeon, Korea ( hcshim@kaist.ac.kr)
© KROS
Abstract
The Global Positioning System (GPS) is widely used to aid the navigation of aerial vehicles. However, the GPS cannot be used indoors, so alternative navigation methods are needed to be developed for micro aerial vehicles (MAVs) flying in GPS-denied environments. In this paper, a realtime three-dimensional (3-D) indoor navigation system and closed-loop control of a quad-rotor aerial vehicle equipped with an inertial measurement unit (IMU) and a low-cost light detection and ranging (LIDAR) is presented. In order to estimate the pose of the vehicle equipped with the two-dimensional LIDAR, an octree-based grid map and Monte-Carlo Localization (MCL) are adopted. The navigation results using the MCL are then evaluated by making a comparison with a motion capture system. Finally, the results are used for closed-loop control in order to validate its positioning accuracy during procedures for stable hovering and waypoint-following
Keywords:
3-D Indoor Navigation, Autonomous Navigation System, Monte-Carlo Localization, Octree Grid Mapping, Micro Aerial Vehicle서 론
지난 십수년간 GPS (Global Positioning System)를 항법 장치로 사용함으로써 야외에서 비행하는 무인항공기의 자 율비행 기술은 크게 발전하였다. 그리고 최근 소형/고성능 의 관성항법센서, 마이크로컨트롤러, 리튬-폴리머(Li-Po) 배 터리, 모터 기술이 발전함에 따라 이제는 실내에서도 소형 무인항공기(Micro Aerial Vehicle)를 안정적으로 비행할 수 있게 되었다. 그러나 아직까지 건물 내부 또는 지하와 같은 실내에서는 여전히 GPS를 사용할 수 없다. 따라서 이러한 실내 환경에서도 무인항공기의 자율비행이 가능하 도록 하기 위해서는 무인항공기에 장착된 센서만을 사용 하는 자율적인 위치추정 방법이 필요하며, 그런 방법은 실 외에서도 차폐 또는 전파방해에 의해 GPS가 사용 불가능 할 경우 매우 유용하게 사용될 수 있을 것이다.
로봇 및 무인항공기의 자율 항법을 위해서 카메라를 사 용하여 항법을 추정하는 방법[1-7]이 주로 연구되어 왔지만, 최근들어 소형 무인항공기에 탑재할 수 있는 소형 및 경 량의 2-D LIDAR (Two-dimensional Light Detection and Ranging)가 개발되면서 이를 사용해 2차원 평면에서의 Scan-matching과 SLAM (Simultaneous Localization and Mapping) 기반의 자율항법[8-10]이 연구되었다. 그리고 최근 에는 3차원 점유격자지도 기반의 무인항공기 실시간 위치 추정에 관한 연구[11,12]도 진행되고 있다. 그러나 수십미터 를 측정할 수 있는 고가의 2-D LIDAR와 각종 센서 및 컴 퓨터를 장착한 무인항공기는 추락할 경우 비용 측면의 손 실이 크기 때문에 좁은 실내 및 장애물 환경에서 적극적 인 실험이 꺼려지게 된다.
따라서 본 논문에서는 저가형 LIDAR가 장착된 무인항 공기가 3차원 실내지도 내에서 실시간으로 자기위치를 추 정하는 기법을 제시한다. 먼저, 수미터 이내의 짧은 거리 만 측정가능한 저가의 2-D LIDAR 및 관성측정장치(IMU: Inertial Measurement Unit)가 장착된 실내비행용 무인항공기 시스템의 구성을 설명하고, 실내 지도작성 및 위치추정에 효율적으로 사용될 수 있는 Octree기반 3차원 지도작성기 법과 작성된 지도에서의 몬테카를로 위치추정기법(MCL: Monte-Carlo Localization)을 설명한다. 제시한 항법을 사용 한 실내 자동비행 실험결과와 모션캡쳐시스템의 측정결과 를 비교하고 그 결과를 고찰하였다.
본 론
실내항법을 위한 2-D LIDAR 및 IMU가 탑재된 쿼 드로터 플랫폼 구성
실내 비행실험용 쿼드로터 기반 무인항공기의 하드웨어 및 소프트웨어 구성은 다음과 같다. 실험에 사용된 쿼드로 터 프레임은 모터간 거리 45 cm, 중량 1.6 kg의 소형 기체 이며 프레임의 하부에는 Li-Po 배터리 및 Gumstix기반의 소형 비행제어컴퓨터가 장착되어 있다. 중앙 상단에는 Microstrain 3DM-GX3-25 IMU와 최대측정거리 4 m의 Hokuyo URG-04LX LIDAR가 장착되어 있다.
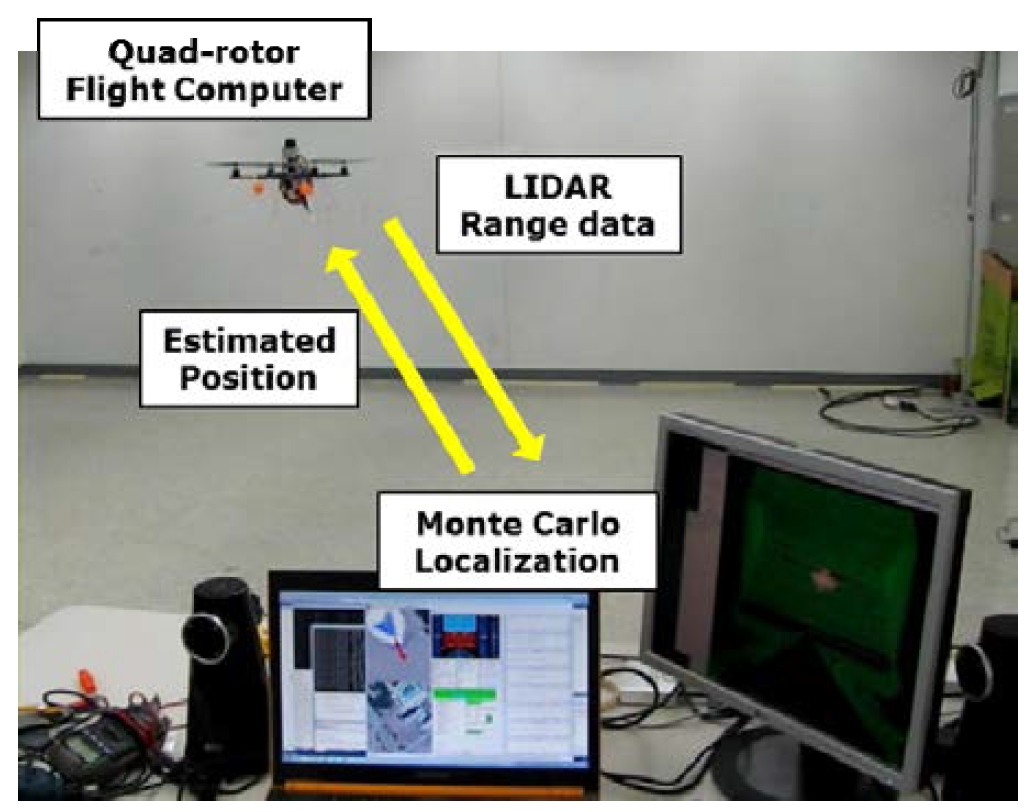
Fig. 1과 같이 LIDAR의 후방 좌/우 부분에는 반사거울을 장착하였고, 이를 통해 LIDAR의 레이저를 일부분 반사시 켜 무인항공기의 전면 180°뿐만 아니라 상/하 방향으로도 거리측정이 가능하다. LIDAR 거리측정 데이터는 블루투스 (Bluetooth) 어댑터를 거쳐 무선통신으로 지상 컴퓨터에 전 송된다. 지상 컴퓨터로는 Intel i7 CPU 기반 노트북 컴퓨터 를 사용하였으며, 무인항공기에서 전송받은 LIDAR 데이 터에 MCL을 적용해 무인항공기의 현재 위치 및 자세를 계산한다. 계산된 무인항공기의 위치/자세 정보는 Wi-Fi를 통해 다시 무인항공기로 전송된다. Fig. 2.
무인항공기에 장착된 비행제어컴퓨터는 Wi-Fi로 전송받 은 위치/자세 추정결과와 IMU 측정값을 확장칼만필터 (EKF: Extended Kalman Filter)로 결합해 최종 항법해를 계산 한다. EKF는 많은 무인항공기에서 사용되는 GPS-aided INS (Inertial Navigation System)와 같은 구조이지만 실외의 위치 정보를 제공하는 GPS를 대신하여 본 논문에서 제시하는 실내 위치추정값을 입력받도록 하였다. 무인항공기에 장착 된 비행제어컴퓨터에 비행제어를 위한 Multi-loop PID 제어 기를 구성하였고, 계산된 비행제어명령은 4개의 모터 컨트 롤러에 각각 인가된다. 이를 통해 무인항공기는 실내에서 위치, 속도, 자세를 제어하여 주어진 경로점을 추종하며 자동으로 비행할 수 있다.
3-D Monte-Carlo Localization
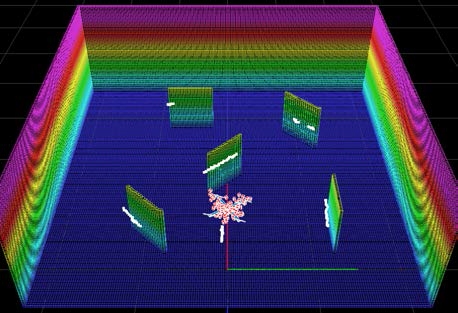
본 연구에서는 무인항공기의 실시간 3차원 위치추정을 위하여 Octree 기반 점유격자지도(Occupancy Grid Map)에서 의 2-D LIDAR 측정값을 이용한 몬테카를로 위치추정기법 을 수행하였다. Octree는 3차원 공간을 계층적으로 분할하 여 표현할 수 있는 데이터 구조로써 이를 사용하면 복잡 한 물체의 3차원 세부형상을 보다 효율적으로 저장할 수 있고, 저장된 데이터를 빠르게 읽어 지도 정보 계산과 화 면에 출력하기 위한 목적으로 사용할 수 있다[13]. Octree기 반의 지도작성기법을 사용해 약 8.0 x 9.0 x 2.5 m 크기의 실 험실 환경의 3차원 지도를 Fig. 3과 같이 작성하였다. 이 지 도의 가장 작은 단위 셀인 unit voxel (volumetric pixel)의 직 경은 5 cm이며, 약 60,000개의 unit voxel이 사용되었다.
무인항공기의 위치 및 자세의 실시간 추정을 위해 파티 클 필터(Particle Filter)에 기반한 몬테카를로 위치추정기법 을 사용하는데, 이 기법은 점유격자지도가 주어진 환경에 서 기체의 위치/자세에 의한 파티클의 Sampling, 측정값과 의 Likelihood 계산, Resampling 단계를 반복하여 항법결과 로 평균값과 공분산 값을 제공한다[14]. 베이지안 필터에 기 반한 로봇 위치/자세의 확률 모델은 다음 식과 같이 표현 할 수 있다.
| (1) |
위 식에서 xt, ut, zt, mo, η 는 각각 무인항공기의 State, IMU 입력값, LIDAR 측정값, Octree grid map, 그리고 Scale factor이다.
무인항공기의 6-DOF 위치 및 자세를 모두 MCL로 추정 하려면 파티클의 양이 증가하고 이에 따른 계산량이 커지 므로 실시간 처리가 어려워진다. 따라서 본 연구에서는 무 인항공기의 Roll 및 Pitch 자세는 장착된 IMU를 이용해 바 로 계산하고, 3차원 위치 및 Yaw 자세를 포함한 4개의 State만을 MCL로 추정해 계산의 실시간성을 확보하였다.
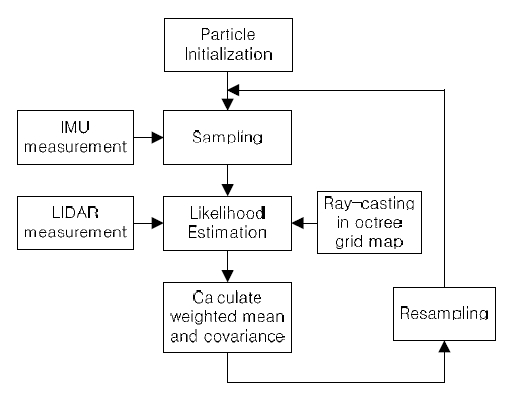
본 논문에 사용된 MCL의 전체 흐름은 Fig. 4의 순서도 와 같이 요약할 수 있다. 먼저, Sampling 단계에서는 아래 의 식과 같이 비행체의 motion model에 기반하여 무인항공 기 State에 IMU 적분값의 증분 Δximu 과 가우시안 랜덤 노 이즈 wt 를 더한다.
| (2) |
Likelihood 계산 과정에서는 다음 측정모델에 기반하여 Octree 지도와 LIDAR 측정값으로 각 파티클의 확률을 계 산한다. 아래의 식에서 σhit 은 LIDAR beam model의 파라 미터이며, zt 과
| (3) |
무인항공기의 고도는 위/아래로 반사된 수십 개의 LIDAR 측정값들에서 이상치(outlier)를 제거한 중간값 (median)과 현재 무인항공기 위치 및 자세에서 수직 위/아 래 방향 Ray-casting이 만나는 격자 셀의 고도를 더하여 사 용한다.
마지막으로 파티클의 Likelihood에 따른 가중치 합을 구 하여 최종 항법 결과인 무인항공기의 위치 평균과 분산을 계산한다. 계산된 항법 결과는 Wi-Fi를 통해 무인항공기에 전송되고, 파티클은 Resampling되어 다시 다음번 항법 계 산에 사용된다.
Experiment
본 연구에서 제시한 실시간 위치추정 알고리듬의성능을 평가하기 위해 Fig. 5와 같이 모션캡쳐시스템이 설치된 장 소에서 비행실험을 수행하였다. 비행실험을 위해 실내 3차 원 지도를 Fig. 3과 같이 작성하였으며, 그 지도 내 공간에 지정된 경로점을 따라 약 100초간 자동으로 비행하였다. MCL 항법결과를 실시간으로 사용해 자동비행을 수행하였 으며, 모션캡쳐시스템은 이와 별도로 LIDAR위에 장착된 마커의 위치를 기록하여 항법결과를 비교하는 용도로만 사용되었다.
MCL에 사용된 파티클 수는 약 100-120이며 이보다 파 티클 수를 줄이면 더 빠른 추정이 가능한 반면에 움직임 에 대한 반응이 늦어지고 심할 경우 추정에 실패하여 실 제 비행체와 다른 위치에 파티클이 수렴하는 현상이 발생 할 수 있다. 이와 반대로, 이보다 파티클을 늘리면 빠른 움 직임에 대하여 추정에 실패하는 현상은 줄어들지만 계산 시간이 늘어나 항법 출력이 지연되므로 무인항공기의 제 어 성능이 저하된다. 현재 실험장비 구성으로 MCL의 1회 계산시간은 약 80-140 ms를 유지하고 있다. LIDAR의 전송 지연을 제외한 MCL 계산시간이 약 200 ms을 초과하면 호 버링 제어시 한 위치에 수렴하지 못하고 진동하게 되며, 결국 위치가 반경 1 m를 초과하게 되어 실내 비행이 어려 워진다.
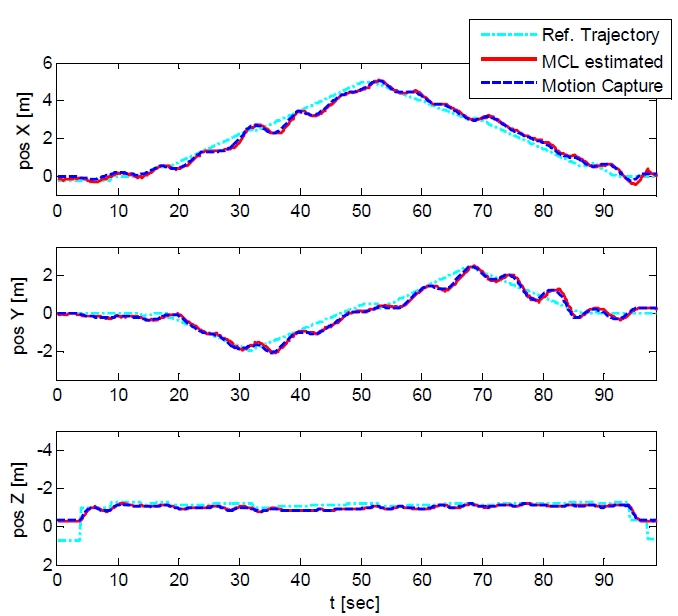
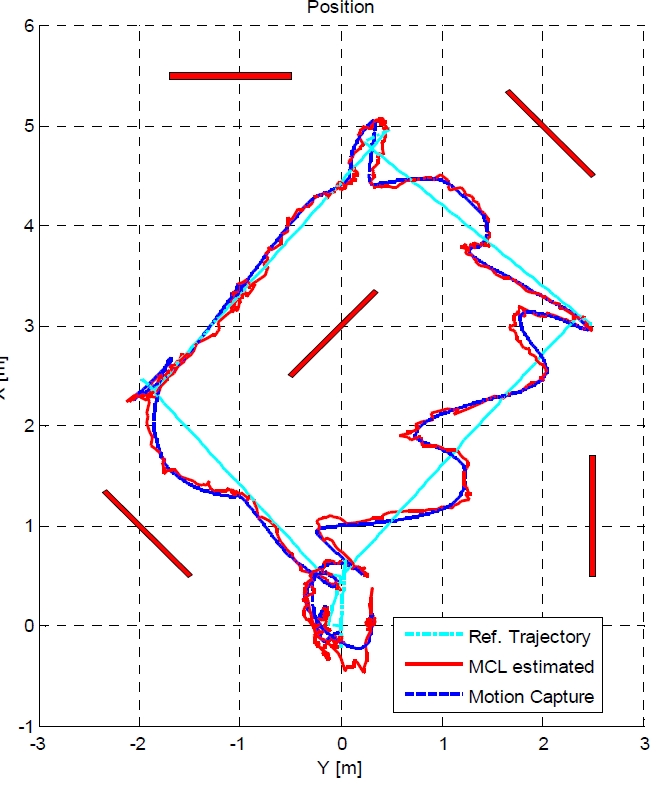
Fig. 6 및 Fig. 7의 그래프는 LIDAR를 사용한 MCL 방법 으로 추정한 3차원 항법결과와 모션캡쳐시스템으로 측정 한 위치를 보여준다. MCL 계산시간 및 통신 지연 때문에 순간적으로 제어 성능이 저하되어 주어진 비행경로를 약 간씩 벗어나는 경우는 있지만, 추정한 무인항공기의 궤적 은 모션캡쳐시스템과 거의 유사함을 Fig. 6 및 Fig. 7에서 확인할 수 있다.
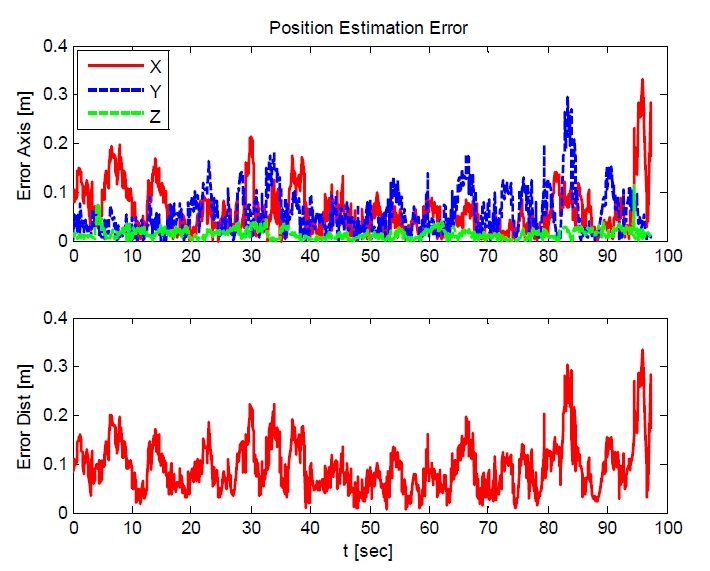
Fig. 8은 비행시간 동안 측정된 위치 오차를 보여주며, 전체 비행실험 중의 RMSE (Root mean square error)는 0.16 m 로 기록되었다. 1000 Hz의 측정 주기 및 0.5 mm의 오차로 위치를 측정하는 모션캡쳐시스템에 비교할 때, 최대 스캔 주기 10 Hz의 저가형 LIDAR를 사용해 MCL로 추정한 3차 원 항법은 다소 부드럽지는 않으나 그 위치추정 결과는 상당히 정밀함을 확인할 수 있다.
다만 Hokuyo UTM-30LX와 같이 최대 30 m의 거리를 40 Hz로 측정할 수 있는 고가의 LIDAR에 비해 센서의 측정 속도가 느리므로 무인항공기의 빠른 기동 시에는 항법계 산에 지연이 발생하는 취약점이 존재한다. 하지만 실내에서 비행하는 쿼드로터 무인항공기는 안정성 및 충 돌위험 때문에 빠른 속도로 비행할 수 없는 경우가 많다. 따라서 이를 고려하면 오히려 본 논문에서 제안한 저가형 LIDAR를 사용하는 실내항법 시스템이 다수의 무인항공기 를 운용하거나 충돌위험이 높은 좁은 공간, 또는 벽이나 구조물에 의해 가려져 모션캡쳐시스템을 사용할 수 없는 공간에서의 각종 실험을 수행하기에 비용측면에서 적합할 수 있다.
또한 MCL을 사용하는 항법은 3차원 지도의 부정확성에 도 일정 수준의 강건성이 유지된다. LIDAR 측정값과 지도 간의 유사한 부분이 많을 수록 높은 Likelihood를 가지게 되는 파티클 필터의 특성상 위치 추정의 모호성을 크게 증가시키지 않는 범위 내에서의 환경 변화는 용인된다. 따 라서 실제 환경이 제작된 지도와 부분적으로 다르거나 비 행 중에 사람이 무인항공기로 접근하더라도 위치추정 정 밀도를 유지할 수 있으므로 복잡하고 동적인 3차원 환경 에서의 정밀한 실내 비행에 더욱 적합하다고 볼 수 있다.
결 론
본 논문에서는 저가형 2-D LIDAR를 장착한 소형 무인 항공기의 실시간 3차원 실내 항법과 이를 이용한 자동비 행 결과를 제시하였다. Octree를 기반으로 한 3차원의 실내 지도에서 Monte-Carlo Localization을 적용함으로써 저가의 2-D LIDAR와 IMU를 장착한 무인항공기도 실내에서의 정밀 한 3차원 자동비행이 가능함을 확인할 수 있었다. 본 연구에 서 제안한 기법을 사용하면 저비용으로도 실내 환경에서 비 행하는 무인항공기의 항법을 제공할 수 있으므로 다양한 실 내 비행실험 및 임무수행에 응용될 수 있을 것이다.
REFERENCES
-
Kim, J, Sukkarieh, S, “Real-time Implementation of Airborne Inertial-SLAM”, Robotics and Autonomous Systems, (2007), 55(1), p62-71.
[https://doi.org/10.1016/j.robot.2006.06.006]

-
Steder, B, Grisetti, G, Stachniss, C, Burgard, W, “Visual SLAM for Flying Vehicles”, IEEE Transactions on Robotics, (2008), 24(5), p1088-1093.
[https://doi.org/10.1109/tro.2008.2004521]

-
Ahrens, S, Levine, D, Andrews, G. G, How, J. P, “Vision-based Guidance and Control of a Hovering Vehicle in Unknown, GPS-denied Environments”, (2009, May), IEEE International Conference on Robotics and Automation (ICRA).
[https://doi.org/10.1109/robot.2009.5152680]

-
Weiss, S, Scaramuzza, D, Siegwart, R, “Monocular- SLAM–Based Navigation for Autonomous Micro Helicopters in GPS-Denied Environments”, Journal of Field Robotics, (2011), 28(6), p854-874.
[https://doi.org/10.1002/rob.20412]

-
Fraundorfer, F, Heng, L, Honegger, D, Lee, G. H, Meier, L, Tanskanen, P, Pollefeys, M, “Vision-Based Autonomous Mapping and Exploration Using a Quadrotor MAV”, (2012), IEEE International Conference on Intelligent Robots and Systems (IROS).
[https://doi.org/10.1109/iros.2012.6385934]

-
Han, J, Ok, J, Chung, W. K, “Localization and Autonomous Control of PETASUS System II for Manipulation in Structured Environment”, Journal of Korea Robotics Society, (2013), 8(1), p037-042.
[https://doi.org/10.7746/jkros.2013.8.1.037]

-
Huh, S, Shim, D. H, Kim, J, “Integrated Navigation System using Camera and Gimbaled Laser Scanner for Indoor and Outdoor Autonomous Flight of UAVs”, (2013), IEEE International Conference on Intelligent Robots and Systems (IROS).
[https://doi.org/10.1109/iros.2013.6696805]

-
Bachrach, A, Prentice, S, He, R, Roy, N, “RANGE—Robust Autonomous Navigation in GPSDenied Environments”, Journal of Field Robotics, (2011), 28(5), p644-666.
[https://doi.org/10.1002/rob.20400]

-
Shen, S, Michael, N, Kumar, V, “Autonomous Multi-Floor Indoor Navigation with a Computationally Constrained MAV”, (2011, May), IEEE International Conference on Robotics and Automation (ICRA).
[https://doi.org/10.1109/icra.2011.5980357]

-
Grzonka, S, Grisetti, G, Burgard, W, “A Fully Autonomous Indoor Quadrotor”, IEEE Transactions on Robotics, (2012), 28(1), p90-100.
[https://doi.org/10.1109/tro.2011.2162999]

-
Huh, S, Cho, S, Shim, D. H, “3-D Grid Mapping and Monte Carlo Localization Method for Indoor Navigation of UAVs”, (2012, April), KSAS (Korean Society for Aeronautical and Space Sciences) Spring Conference.
[https://doi.org/]

-
Bry, A, Bachrach, A, Roy, N, “State estimation for aggressive flight in GPS-denied environments using onboard sensing”, (2012, May), IEEE International Conference on Robotics and Automation (ICRA).
[https://doi.org/10.1109/icra.2012.6225295]

-
Hornung, A, Wurm, K. M, Bennewitz, M, Stachniss, C, Burgard, W, “OctoMap: An Efficient Probabilistic 3D Mapping Framework based on Octrees”, Autonomous Robots, (2013), 34(3), p189-206.
[https://doi.org/10.1007/s10514-012-9321-0]

-
Thrun, S, Burgard, W, Fox, D, Probabilistic Robotics, (2005), MIT Press.
[https://doi.org/]