[ ARTICLE ]

Journal of Korea Robotics Society - Vol. 9, No. 2, pp.117-123

ISSN: 1975-6291 (Print) 2287-3961 (Online)

Print publication date May 2014

Received 13 Feb 2014 Revised 30 Mar 2014 Accepted 23 Apr 2014

DOI: https://doi.org/10.7746/jkros.2014.9.2.117

COAG 특징과 센서 데이터 형상 기반의 후보지 선정을 이용한 위치추정 정확도 향상

김동일¹ ; 송재복^† ; 최지훈²

1기계 공학, 고려 대학교 astronovic@korea.ac.kr
2UGV 기술 이사회, 국방 개발기구 ji_hoon_choi@add.re.kr

Improvement of Localization Accuracy with COAG Features and Candidate Selection based on Shape of Sensor Data

Dong-Il Kim¹ ; Jae-Bok Song^† ; Ji-Hoon Choi²

1Mechanical Engineering, Korea University astronovic@korea.ac.kr
2UGV Technology Directorate, Agency for Defense Development ji_hoon_choi@add.re.kr

※This research was supported by the UTRC (Unmanned Technology Research Center) at KAIST, originally funded by DAPA and ADD.
†Corresponding author: Mechanical Engineering, Korea University, Anam-Dong, Seongbuk-Gu, Seoul, Korea ( jbsong@korea.ac.kr)

Abstract

Localization is one of the essential tasks necessary to achieve autonomous navigation of a mobile robot. One such localization technique, Monte Carlo Localization (MCL) is often applied to a digital surface model. However, there are differences between range data from laser rangefinders and the data predicted using a map. In this study, commonly observed from air and ground (COAG) features and candidate selection based on the shape of sensor data are incorporated to improve localization accuracy. COAG features are used to classify points consistent with both the range sensor data and the predicted data, and the sample candidates are classified according to their shape constructed from sensor data. Comparisons of local tracking and global localization accuracy show the improved accuracy of the proposed method over conventional methods

Keywords:

Monte Carlo Localization, Particle Filter, Localization, COAG Features

1. 서 론

로봇이 다양한 환경을 주행하기 위해서는 환경 정보를 이용하여 로봇 위치를 추정하는 기술, 최적화된 주행 경로 를 생성하고, 장애물을 회피하기 위한 기술 등이 필요하다 ^[1-3]. 로봇의 위치를 정확하게 파악하는 것이 다른 기술을 원활하게 수행하기 위해 필수적이므로, 위치추정은 가장 중요한 기술이다. 특히, 실외환경에서 로봇의 위치추정은 GPS를 사용하여 개발되어 왔으나^[4], GPS 정보는 건물이나 장애물이 많은 환경에서 불확실성이 높아진다는 단점이 있다. 그러므로 GPS 신호가 들어오지 않는 상황을 고려해 야 하는 국방 관련 분야에서는 사전 환경지도와 센서융합 기반의 위치추정 기술에 대한 많은 연구가 진행되고 있다. 대표적으로는, 마코프 위치추정, 칼만필터 기반의 위치추 정, 파티클 필터 기반의 Monte Carlo Localization(MCL) 등이 연구되었다^[5]. 이런 다양한 위치추정 기술 중에 MCL^[6]은 야외환경에서 로봇 위치에 대한 불확실성을 줄이고 환경 변화에 강인하게 작용하는 장점이 있다.

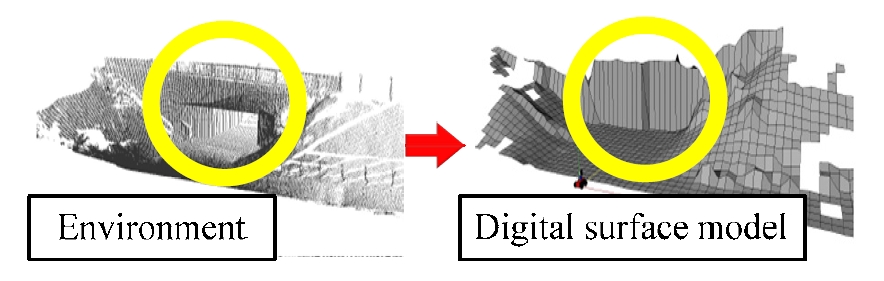
이와 관련된 연구로서 다층 표면지도(multi-level surface map)와 같은 지도를 이용하여 위치추정을 수행한 연구가 있는데^[7], 이 연구는 널리 사용하는 지도를 사용하지 않아 일반적인 지도 기반의 기술을 사용할 수 없다는 단점이 있다. 따라서 본 연구에서는 실외환경에 대한 기본 지도로 DSM(digital surface model)을 사용한다. 그림 1은 본 연구의 실험 환경과 이를 나타내는 DSM이다. 이 지도는 실험 환 경을 작은 격자(0.25m x 0.25m)로 나누는데, 각 격자는 하나 의 고도정보를 가진다. 이러한 지도는 항공 레이저 측량 (Light Detection and Ranging(LiDAR) 시스템을 항공기에 장착하여, 레이저 펄스를 지표면에 주사하고, 반사된 레이저 펄스의 도달시간을 측정함으로써 반사 지점의 공간 위치 좌표를 계산해 내어 지표면에 대한 지형정 보를 추출하는 측량 기법)을 이용하여 작성되며, 실외환 경을 표현하는 대표적인 지도로서 지질분석 및 군사용 로 봇 등 다양한 분야에서 사용하고 있다^[8].

DSM을 이용하여 정밀한 MCL을 수행하기 위하여, 이전 연구에서는 COAG(commonly observed from air and ground)^[9] 특징을 추출하여 환경정보로부터 예측한 센서 데이터와 실제 센서 데이터가 유사한 지점을 선별하여, 이를 후보지 로 선정하는 알고리즘을 접목하여 위치추정 성능을 향상 시켰다^[10]. 본 연구에서는 이를 개선하기 위하여 센서 데이 터의 형상(shape)을 이용한 후보지 선정 기법을 제안하였 다. 새로운 후보지 선정 기법을 이용한 MCL은 이전 연구 보다 우수한 위치추정 정확도를 가지며, 이를 실제 환경에 서 수집한 실시간 센서 데이터를 이용한 전역 및 국부 위 치추정 시뮬레이션으로 증명하였다.

본 논문의 구성은 다음과 같다. 2장에서는 COAG 특징 추출 기법에 대하여 간략하게 설명하고, 3장에서는 제안한 후보지 선정 기법에 대하여 기술한다. 4장에서는 본 연구 에서 개발한 기술을 이용한 시뮬레이션 결과에 대해 설명 하고, 마지막으로 5장에서 전체 내용에 대한 결론을 언급 한다.

2. COAG 특징 추출 기법

본 장에서는 DSM의 한계를 극복하기 위해 개발된 COAG 특징 추출 기법에 대하여 간략하게 설명한다^[9]. DSM은 환경을 동일한 격자로 나누어 표현하며, 각 격자 는 격자 내에서 가장 높은 하나의 고도를 가진다. 따라서 그림 2에서 원으로 표시한 다리는 아래가 비어 있어서 로 봇이 자유로이 다닐 수 있는 환경임에도 불구하고, DSM에 서는 막혀 있는 벽 환경으로 처리되어 로봇이 지나다닐 수 없게 된다. 따라서 실제 거리센서로 측정한 데이터와 지도를 이용하여 예측한 데이터가 달라진다. COAG 특징 추출 기법은 필드로봇이 거리센서로 측정한 지형 데이터 와 DSM으로부터 예측한 지형 데이터가 유사한 지점을 탐 색한다.

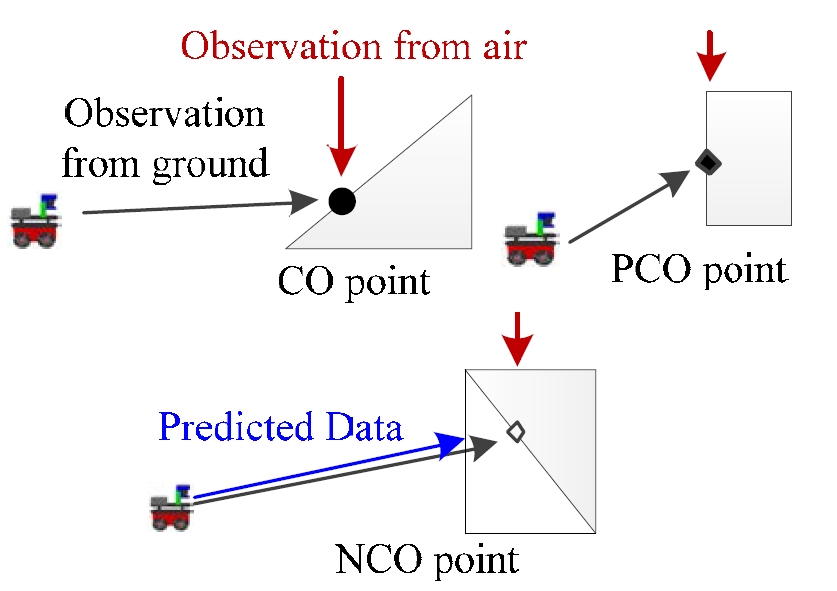
COAG 특징은 2차원 레이저 스캐너를 상하로 틸팅하면 서 추출한다. 지면과 평행한 평면에 배치된 센서 위치에서 위로 45도까지 회전시키며 레이저 스캔 데이터를 수집하 면, 로봇 주변의 실외환경에 대한 거리데이터를 3차원 점 군(point cloud)으로 얻을 수 있다. 점군을 분석하면 그림 3 과 같이 레이저 스캐너의 각도에 따른 지형 데이터의 배 치를 측정할 수 있다.

데이터 배치를 분석하면 환경의 형상에 따라 다음의 4 가지로 분류할 수 있다. 첫째로, CO(commonly observed) 지 점은 센서로 감지하는 방향에서 측정된 지점보다 높이 위 치한 점들이 측정된 지점보다 높이 있는 점들이 멀리 위 치한 경우이며, 항공에서 측정한 고도지도상의 데이터와 지상에서 관측하는 센서 데이터가 가장 유사할 수 있는 지점이다. 둘째로, PCO(potentially commonly observed) 지점 은 측정된 지점보다 높이 있는 점들이 유사한 높이에 위 치한 경우이다. 벽과 같은 환경에서 데이터를 수집하였을 때 추출이 가능하며, CO 지점에 비해 실제 센서 및 예측한 데이터 간의 유사도가 떨어진다. 셋째로, NCO(not commonly observed) 지점은 측정된 지점보다 높이 있는 점 들이 로봇에 가까이 위치한 경우이며, 이러한 환경을 고도 지도에서는 정확하게 표현할 수 없으므로 예측한 거리와 실제 센서 데이터간의 오차가 크게 발생할 수 있다. 그림 3에서 보듯이 NCO 지점을 측정한 각도로 DSM을 이용하 여 관측정보를 예측하면 실제 센서데이터와 차이가 있다. 마지막으로, UN(unknown) 지점은 위 세 특징의 조건에 맞 지 않아 데이터 간의 유사도를 판별할 수 없는 부분을 의 미한다.

3. 센서 데이터 형상 기반 후보지 선정 기법을 사용한 위치추정

본 장에서는 COAG 특징 정보를 활용하여 센서 데이터 를 다각형 모델로 만들고, 예측 데이터로 만든 다각형과 실제 센서 데이터로 만든 다각형을 비교하여 후보지를 선 정하는 방법에 대하여 설명한다.

3.1. 센서 데이터로 수립한 다각형 및 유사도 지표

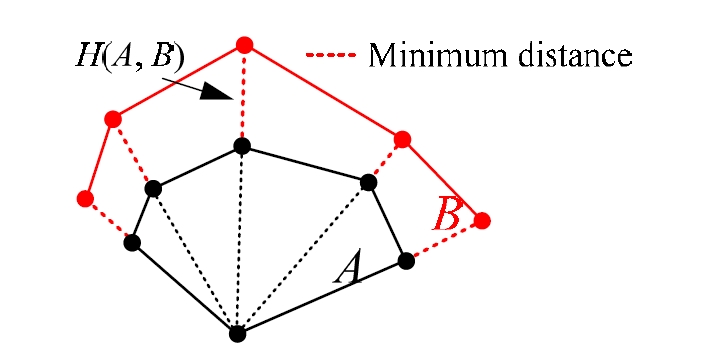
먼저, 임의의 로봇 위치에서 센서 데이터를 수집하여 CO 지점 및 PCO 지점만을 추출하고, 추출한 특징들을 실 선으로 이어 그림 4의 다각형 A를 생성한다. 또한, 임의 위치의 각 샘플에서 각 특징의 각도와 동일한 방향에서의 센서 데이터를 예측하고, 이를 이용하여 다각형 B를 생성 한다. 유사도 지표란 언급한 두 도형의 형상에 대한 유사 도를 나타낼 수 있는 지표를 의미한다. 본 연구에서는 두 도형의 위치와 무관하게 형상만을 비교하기에 용이한 Hausdorff 거리^[11]와 두 도형의 평균 최소거리를 이용하여 유사도 지표를 수립한다.

Hausdorff 거리는 각 도형의 꼭지점을 기준으로 거리를 비교하여 각 점 간의 최소거리들 중 가장 긴 거리를 의미 한다. 그림 4에서의 5개의 최소거리 중에서 가운데 거리가 가장 크므로, 이 최소거리가 Hausdorff 거리가 되고 H(A, B) 로 나타낸다.

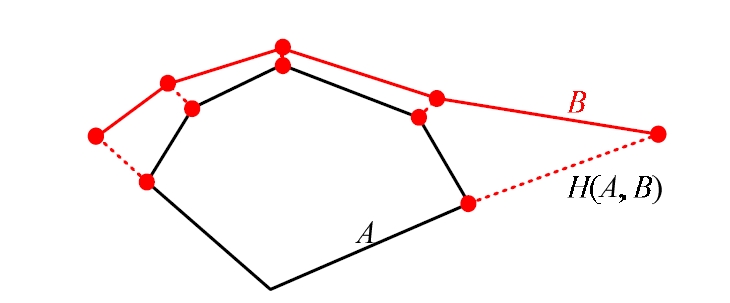
또한, 이들 5개의 최소거리의 평균으로부터 평균 최소거 리를 구할 수 있다. 그림 5와 같이 지도와 환경간의 정보 차이로 인해 일부 센서 데이터의 오차가 큰 지점이 발생 하면 Hausdorff 거리만으로 두 다각형의 유사도를 비교하 는 것이 부정확하므로, 이러한 경우를 대비하여 평균 최소 거리를 함께 사용한다.

위에서 정의된 두 거리는 서로 다른 척도로서 상호간의 연관성이 작으므로, 유사도 지표는 두 거리에 대해 각각 수립한다. 각 지표는 도형의 형상이 유사할수록 커져야 하 고, 확률은 0과 1사이에 수렴해야 하므로, Hausdorff 거리에 대한 지표 E_Hausdorff와 평균 최소거리에 대한 지표 E_mean는 다 음과 같이 수립하였다.

E Hausdroff = d max - H A, B n d max

(1)

E mean = d max - d mean A, B n d max

(2)

3.2. 수립한 지표 기반의 후보지 선정

MCL에서는 임의로 분포된 샘플 위치에서의 예측 정보 와 실제 센서 데이터 간의 유사도를 비교하여 위치추정을 수행한다. 따라서 샘플 후보지를 실제 로봇 위치와 유사한 곳에 선정하면 위치추정 정확도를 높일 수 있다. 제시한 두 거리는 작아질수록 두 도형이 유사하므로, 식 (1) 및 (2) 의 유사도 지표는 커질수록 두 도형이 유사하다. 이를 이 용한 후보지 선정 알고리즘은 아래와 같다.

Input : m
for all samples ndo
for all measurements to CO point i
d_mean = average(D(A,B(n))
ifE_Hausdorff >σand Emean >σthen
E(n) = 1
else
E(n) = 0
end if
end for
end for

위 알고리즘에서 m은 필드로봇에서 측정한 센서데이터 와 각 샘플에서 지도로부터 예측한 데이터를 의미하며, 샘 플이 실제 로봇 위치와 유사한 곳에 배치되었는지를 판단 하는 척도로 E(n)을 제시한다. D(A, B(n))은 도형 A와 도형 B(n)의 모든 최소거리들의 집합이다. 실제 센서 데이터로 만든 도형 A와 n번째 샘플에서 예측한 정보로 만든 도형 B(n)을 이용하여 Hausdorff 거리와 평균 최소거리를 각각 구하고, 이를 이용하여 유사도 지표를 계산한다. 계산한 값이 임계값 σ보다 작을 경우, 후보지가 아니라 판단한다. 이와 같은 후보지 선정 기법을 적용하면 800 x 800개의 격 자로 구성되는 지도 상에 무작위로 20,000개의 샘플을 배 치할 때, 그림 6과 같은 결과를 얻을 수 있다.

위 그림에서 초기위치(Initial position)란 지도상에서 로봇 의 주행 시작지점을 의미한다. 그림에서 보듯이, 무작위로 샘플이 배치되지 않고, 선별된 모습을 볼 수 있다. 이러한 후보지 선정과정은 매 위치추정 시 반복하여 수행되며 많 은 샘플들이 지도상에서의 실제 로봇 위치와 가까운 곳에 분포하게 되어 위치오차가 감소하게 된다.

3.3. 가중치 부여(importance weighting)

가중치 부여 과정은 샘플을 사용하는 MCL에서 로봇 위치와 샘플 위치 간의 유사도를 결정하는 과정이므로 매 우 중요하다. 가중치는 어떤 샘플 위치에서 예측한 센서 데이터와 실제 센서 데이터를 비교하여 센서 모델을 수립 하여 구한다. 샘플 n에 대한 가중치는 베이시안 갱신규칙 에 기반하여 확률적으로 아래와 같이 표현할 수 있다^[3].

ω t n = bel x t n bel - x t n = η ⋅ p z t x t n

(3)

위 식에서 η는 정규화 상수를 의미하며, ω_t⁽ⁿ⁾는 가중치, z_t 는 관측한 센서 데이터, x_t⁽ⁿ⁾는 시간 t에서의 n번째 샘플의 위치이다. 최종 가중치는 이에 식 (1), (2)를 이용해 도출한 E_t(n)을 곱하여 다음과 같이 나타낼 수 있다.

ω t_final n = ω t n ⋅ E t n

(4)

각각의 샘플은 가중치 부여 과정을 통하여 확률을 갱신 한다. 이런 과정을 반복하여 새로운 샘플을 갱신하며, 후 보지 선정 기법이 적용되어 로봇의 실제 위치 근처에 샘 플이 계속하여 분포하게 된다.

3.4. 위치추정 과정

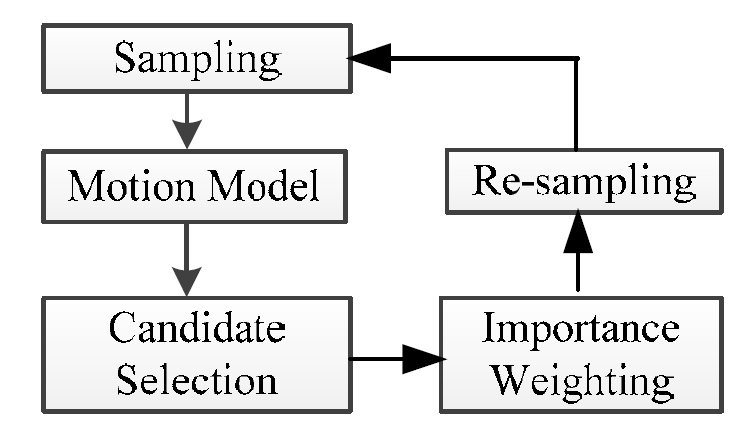
위치추정은 MCL에 본 연구에서 제안한 기법을 적용하 여 수행한다. 본 연구에서는 sampling importance resampling (SIR) 알고리즘이 적용되었다^[12]. 이 알고리즘은 샘플 분포, 가중치 부여, 샘플 재배치의 세 단계로 진행되며, 이 단계 들이 반복되면서 위치추정을 수행한다. 먼저, 샘플 분포 과정 전에 COAG 특징 추출 기법을 수행한다. 초기 샘플 을 분포할 때는 초기 센서 데이터를 이용하여 후보지 선 정 알고리즘을 적용한다.

전체 과정은 그림 7의 흐름도와 같다. 먼저 초기 샘플들 을 배치하면(Sampling), 이동정보를 기반으로 샘플을 이동 시킨다(Motion model). 이동한 샘플의 각 위치에서 후보지 선정(Candidate selection) 및 가중치 부여를 수행하고 (Importance weighting), 얻은 가중치를 기반으로 샘플을 재 배치한다(Re-sampling). 재배치된 샘플은 유사도가 높은 위 치 주변으로 수렴하게 되며, 샘플의 분산도에 따라 계속하 여 미리 설정한 최소 개수까지 계속하여 줄어들게 된다. 이와 같은 과정을 반복하여 위치추정을 수행하고, 실제 위 치와 유사한 가중치를 가진 샘플을 기반으로 로봇의 위치 를 결정한다.

4. 시뮬레이션 결과

본 장에서는 Hausdorff 거리 기반의 후보지 선정을 이용 하여 향상된 위치추정 성능을 검증하고자 한다. 아래의 환경에 대하여 전역 위치추정과 국부 위치추정의 두 종류 의 반복적 시뮬레이션을 통하여 향상된 위치추정 성능을 검증하였다.

4.1. 실험장비 구성

본 연구에서는 그림 8과 같은 Pioneer 3AT 모델을 사용 하여 실험하였다. 장착된 거리센서는 SICK사의 LMS291 모델로, 전방 180°범위를 1°간격으로 최대 80m까지의 거리를 측정할 수 있다. 이 스캐너는 회전 모터와 연결되 어, 지면과 평행한 방향부터 상하로 45°까지 반복 회전되 며 센서 데이터가 수집되었다. 이 로봇은 그림 1의 환경을 주행하며 전역 및 국부 위치추정을 수행하였다.

4.2. 전역 위치추정

전역 위치추정은 로봇의 초기 위치를 모르는 상황에서 지도 전체를 대상으로 로봇의 위치를 추정하는 기술이다. 실험은 20,000개의 샘플로 수행하였다. 위치추정 성공 여 부는 샘플의 수가 500개 이하로 수렴하고, 실제 로봇의 이 동과 유사한 방향으로 이동하고 있을 때 성공하였다고 판 단하였다. 먼저, 20,000개의 샘플을 그림 9의 (a)와 같이 지 도 전체에 임의로 분포하였다. 그림에서 보듯이, 샘플들이 일정한 간격으로 지도 전체에 분포된 것이 아니라, 선별되 어 배치된 모습을 볼 수 있다. 반복적인 MCL 수행을 이용 하여 샘플들은 재분포되고 높은 확률을 가지는 샘플들은 그림 (b)와 같이 수렴하게 된다. 결과적으로, 그림 (c)와 같 이 실제와 유사한 위치로 샘플들이 수렴하게 된다.

4.3. 국부 위치추정

국부 위치추정(local tracking)은 로봇의 초기위치를 알고 있는 상황에서 국부 지역을 대상으로 로봇의 위치를 추정 하는 기술이다. 본 연구에서는 500개의 샘플을 초기위치 주변에 배치하여 시뮬레이션을 수행하였다. 그림 10의 (a) 는 실험 수행 중인 모습이다. 그림에서 보듯이, 샘플이 조 밀하게 수렴하여 로봇의 위치가 실제 위치와 유사하게 추 정되고 있다. 이렇게 반복하여 실험한 결과, 그림 (b)와 같 이 실제와 유사하게 예측 주행경로를 얻었다.

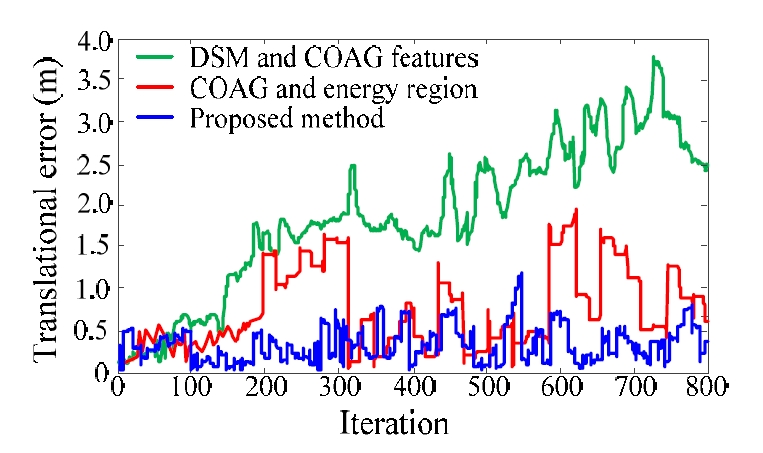
반복된 위치추정 실험을 이용하여 그림 11과 같이 비교 결과를 얻을 수 있었다. 본 결과는 약 100번의 반복 위치 추정 수행을 기준으로 기존의 COAG 특징을 이용한 국부 위치추정 결과^[9]를 초록색 실선으로, 에너지함수 기반 후 보지 선정을 이용한 방법^[10]을 붉은 실선으로나타내어 파 란색 실선으로 표시한 제안된 방법과 반복 수행시 위치오 차를 비교한 것이다. 그래프를 보면 제안한 기법의 결과가 기존의 결과에 비하여 위치오차가 줄어든 모습을 보이며 그래프의 변화폭 역시 감소하여 위치추정의 정밀도가 향 상되었음을 알 수 있다. 전체 추정 결과에 대해 평균 위치 오차를 비교하면, 이전의 기법이 평균 1.9m 및 0.7m의 오 차를 보이는 데 비하여, 제안한 방법은 평균 0.6m의 위치 오차를 보였다.

5. 결 론

본 연구에서는 실외환경에서의 위치추정 기술을 향상시 키기 위하여 센서 데이터를 통해 추출한 COAG 특징을 이 용하여 다각형을 수립하고, 이를 이용한 후보지 선정 방법 을 제안하였다. 선별된 후보지에서 MCL을 수행하여 위치 추정의 정밀도가 향상되었으며 이는 전역 및 국부 위치추 정 시뮬레이션을 통해 검증하였다. 이 방법은 MCL이 아 니더라도 기존의 확률 기반 위치추정 기법에서의 정합에 응용해서 다양하게 사용될 수 있으므로 실용적인 연구라 판단된다.

REFERENCES

Nashashibi, F, Fillatreau, P, Dacre-Wright, B, Simeon, T, “3-D Autonomous Navigation in a Natural Environment,”, (1994), IEEE International Conference of Robotics and Automation, p433-439. [https://doi.org/10.1109/robot.1994.351258]
Noh, C. B, Kim, M. H, Lee, M. C, “Path Planning for the Shortest Driving Time Considering UGV Characteristic and Driving Time and Its Driving Algorithm,”, Journal of Korea Robotics Society, (2013), 8(1), p43-50. [https://doi.org/10.7746/jkros.2013.8.1.043]
Ryu, H, Chung, W. K, “Local Map-based Exploration Strategy for Mobile Robots,”, Journal of Korea Robotics Society, (2013), 8(4), p256-265. [https://doi.org/10.7746/jkros.2013.8.4.256]
Ohono, K, Tsubouch, T, Shigematsu, B, Yuta, S, “Differential GPS and Odometry-based Outdoor Navigation of a Mobile Robot,”, Advanced Robotics, (2004), 18(6), p611-635. [https://doi.org/10.1163/1568553041257431]
Thrun, S, Burgard, W, Fox, D, “Probabilistic Robotics”, (2006), The MIT Press.
Fox, D, “Monte Carlo Localization: Efficient Position Estimation for Mobile Robots,”, (1999), Proc. of AAAI-99, Orlando, FL.
Kummerle, R, Triebel, R, Pfaff, P, Burgard, W, “Monte Carlo Localization in Outdoor Terrains Using Multilevel Surface Maps”, Journal of Field Robotics, (2008), 25(6-7), p346-359. [https://doi.org/10.1002/rob.20245]
Frederick, P, Kania, R, Rose, M. D, Ward, D, Benz, U, Baylot, A, Willis, M. J, Yamauchi, H, “Spaceborne Path Planning for Unmanned Ground Vehicles (UGVs)”, (2005), IEEE Conference of Military Communications (MILCOM), p3134-3141. [https://doi.org/10.1109/milcom.2005.1606139]
Kwon, T. B, Song, J. B, “A New Feature Commonly Observed from Air and Ground for Outdoor Localization with Elevation Map Built by Aerial Mapping System,”, Journal of Field Robotics, (2011), 28(2), p227-240. [https://doi.org/10.1002/rob.20373]
Kim, D. I, Song, J. B, “Accurate Localization with COAG Features and Self-Adaptive Energy Region,”, (2013), The 6th International Conference on Intelligent Robotics and Applications, p576-583. [https://doi.org/10.1007/978-3-642-40852-6_58]
Rucklidge, W, “Efficient visual recognition using the Hausdorff distance”, Lecture Notes in Computer Science, (1995).
Doucet, A, “Sequential Monte Carlo Method in Practice,”, (2001), Berlin, Springer.