야지 고속 주행 로봇을 위한 패시브 메커니즘의 안정성 비교 분석
†Corresponding author: Mechatronics Engineering, Chungnam National University, Gung-Dong, Youseong-Gu, Daejeon, Korea ( jihong@cnu.ac.kr)
© KROS
Abstract
The robot mechanisms that were previously researched had only been conducted for the purpose of overcoming the obstacles stably at low speed driving and enhancing the stability against high speed circuitous driving, and yet, the mechanism satisfying two purposes. However, in order to stably drive with high speed on rough terrain, there is a need for satisfying both of these purposes, as well as testing the efficiency of the mechanisms at high speed driving. There, this paper simulated some of the passive mechanisms and focused on checking the performances of passive mechanisms through simulations and analyzing each mechanism on the basis of an evaluation index. The simulation was conducted by Adams (The Multi-body Dynamics Simulation Solution) and used various types of passive mechanisms which were introduced in the robotics field. As a result, the study confirmed that passive mechanisms have a number of situations that affect the driving stability on each direction of roll and pitch. Further study is needed about active mechanism.
Keywords:
rough terrain, passive mechanism, overcoming the obstacle, stability of turnin, high speed1. 서 론
현재 군사적으로나 재난 구조[1], 탐사 등의 다양한 목적 들에 의해 기존의 차량 메커니즘이 아닌 야지의 특성에 맞게 고속으로 주행 할 수 있는 메커니즘들이 많은 관심 을 받고 있다. 일반적으로 야지 주행을 목적으로 하는 로 봇들은 On-road 상에서의 주행을 목적으로 하는 로봇보다 주행 안정성 부분에 초점을 맞춰 설계가 이루어지며, 야지 라는 환경이 가지는 다양한 특성들로 인하여 다음의 변수 들을 가진다.
첫째는 지형의 생김새 이다. On-road의 경우 장애물이 없 고 평평한 지형인 것에 반해 야지환경은 지면이 고르지 못하고 안정적인 주행을 방해하는 큰 굴곡과 구렁 등의 위험 요소가 많이 존재 한다. 지형의 굴곡으로 인한 로봇 의 무게 중심 변화는 각 바퀴에 작용하는 견인력에 영향 을 주어 경사가 심한 지형을 극복하는데 어려움이 있을 수 있다.
둘째는 지면을 구성하고 있는 지질이다. On-road는 아스 팔트나 콘크리트 등으로 지질의 변화가 없이 고르게 구성 되어 있지만 야지의 경우 잔디, 자갈, 모래, 흙 등 다양한 지질이 복합적으로 구성 되어 있다.
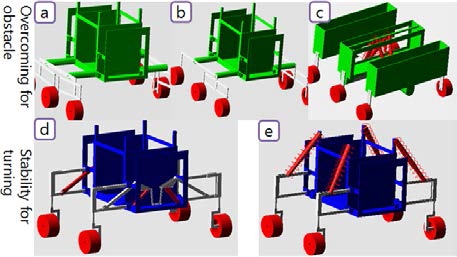
위의 두 요소를 갖는 야지 환경에서는 바퀴가 구렁에 빠져서 헤어나오지 못하게 되거나 고속 주행 시 장애물들 로 인하여 로봇이 전복될 우려가 있다.[2] 따라서 로봇이 최 적화된 주행 궤도를 따라 안정적으로 고속 주행을 하기 위해서 야지의 다양한 지형 및 지질을 안정적으로 극복할 수 있는 구조 설계가 필요하다. 선행 연구에서는 재난 구 조목적의 ROBHAZ-DT3[3], KOH- GA[4]와 탐사를 위한 CRAB[5-7]. RCL-E[7-8], ROBUROC6[9-10] 등 복잡한 제어 알고 리즘을 사용하지 않는 다양한 패시브 타입(Passive type) 메 커니즘의 로봇을 설계하여 장애물이 있는 경우에도 로봇 몸체 안정성을 유지하고자 하였다. 하지만 이러한 메커니 즘들은 대부분 저속 주행을 기준으로 모델링 되었으며 고 속 주행에서 각 메커니즘의 성능을 보장할 수 없다. 또한, 일부 연구에서는 고속 회전에서의 안정성을 유지하기 위 한 목적으로 PUSH ROD SUSPENSION[11-13] 시스템, ANTI ROLL[14-15] 시스템 등의 설계 모델이 있으나 이들은 일반 차량에 적용을 하기 위한 목적으로 설계되어 야지환경에 서 나타나는 장애물을 안정적으로 극복하기 위한 부분은 고려 되지 않았다. 위의 메커니즘들을 분류하여 정리하면 아래의 Table 1과 같다.
Table 1에서 정리된 바와 같이 선행 연구된 로봇 메커니 즘들은 저속 주행 시 장애물을 안정적으로 극복하거나 고 속 선회주행에 대한 안정성만을 증대 시키기 위한 목적으 로 진행되어 왔으며, 두 가지 목적을 만족하는 메커니즘은 연구되지 않았다. 하지만 야지환경에서 안정적으로 고속주 행을 하기 위해서는 위에 제시된 두 가지 목적을 모두 달 성할 필요가 있으며, 위의 메커니즘들의 고속 주행에서의 성능도 확인해 볼 필요가 있다.
본 논문에서는 다물체 동역학 해석 프로그램인 ADAMS 를 사용하여 앞서 제시된 패시브(Passive)타입의 다양한 메 커니즘들을 모델링하고, 장애물을 극복하기 위한 메커니즘 들의 고속 주행 시 안정성 여부와 장애물과 경사가 있는 지형에서의 하중 분배 정도를 분석하여 각 모델들의 구조 적 특징을 비교하고 야지 고속 주행에 적합한 패시브 (passive) 메커니즘을 찾아보고자 한다.
2. 메커니즘 분석을 위한 시뮬레이션 환경
2.1. 메커니즘 분석을 위한 모델의 선정 및 고속에 대한 정의
ADAMS를 통해 시뮬레이션을 하기 위하여 서론에 서 언급한 다양한 메커니즘을 갖는 로봇들을 선정하여 모 델링 하였다.
Fig. 1의 (a), (b), (c) 모델은 Table 1.에서 구분하였듯이, 저 속 주행일 때 장애물을 극복하기 위한 모델들로써, 구동부 가 모두 링크구조로 되어있다. 반면에, (d) 모델은 고속회전 주행에서 안정성을 유지하는 구조를 갖는 모델로써, 각 바 퀴에 독립된 서스펜션(suspension)과 링크 구조를 동시에 갖고 있으며 (e) 모델은 가장 단순한 구조를 갖는 주행 로 봇 모델이다. Fig. 1에 나타난 모든 모델은 각각 고유의 메 커니즘을 그대로 가지고 있다. 하지만, 데이터 분석의 편 의를 위해 모든 모델의 바퀴 크기는 16cm, 로봇의 무게는 50kg로 맞춰주었으며 또한 로봇 몸체의 높이도 통일 시켜 주었다. 추가적으로, 타이어에 대한 변수는 고려하지 않았 고, (c), (d), (e) 모델의 서스펜션의 강성계수(k)와 댐핑계수(c) 는 각 모델의 무게를 고려하여 설정하였다. 그리고 대부분 의 야지 주행 로봇의 최고 속력이 12~14m/s(40~50km/h)정 도인 것을 고려 하여 일반 고속 주행 전차 1/7크기인 a, b, c, d, e가 주행할 수 있는 최고 속력을 14m/s의 1/7인 2m/s로 정의하였다.
2.2. 모델의 주행 안정성 시뮬레이션 지형 선정
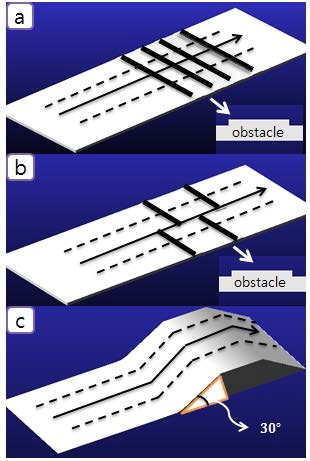
앞 절에서 선정된 모델들의 구조적 성능을 확인하기 위 한 지형을 모델링 하는 것이 필요하다. 본 논문에서는 3개 의 지형을 모델링 하였으며 각각의 지형은 Fig. 2에 나타내 었다. 먼저 Fig. 2의 (a)는 로봇 몸체의 Pitch 방향으로의 움 직임을 확인하기 위한 지형으로, 바퀴지름의 1/2에 해당하 는 높이의 장애물(bump)을 일정한 간격으로 4개를 배치하 였다. (b)는 로봇의 Roll방향으로의 안정성을 확인하기 위한 지형으로 (a)지형과 마찬가지로 바퀴지름의 1/2에 해당하 는 높이의 장애물(bump)을 일정한 간격으로 번갈아 배치 하였다. 마지막으로 (c)는 경사지형에서의 무게 중심 위치 변화를 확인하기 위한 지형으로 경사지형의 기울기는 30°이다.
추가적으로, 실제 야지 환경에서는 다양한 지질의 특성 들로 인하여 마찰계수가 계속적으로 변하지만, 본 논문에 서는 각 로봇들의 구조적 특징만을 비교하기 위하여 시뮬 레이션 상에서 모든 지형의 마찰계수를 0.9로 맞춰주었다.
2.3. 주행 안정성 판단을 위한 평가 지표
본 논문에서 제시하는 시뮬레이션 분석 기준은 크게 두 가지로써 서론에서 제시된 메커니즘 모델을 고속 주행 시 켰을 때 안정성을 유지하는가와 각각의 지형에서 각 바퀴 의 하중이 고르게 유지 되는가 이다. 먼저 장애물을 고속 으로 통과하는 경우 저속으로 주행을 하는 경우 보다 로 봇 몸체의 움직임의 변화가 더 크게 나타날 것을 예측 할 수 있다. 만약 몸체 움직임의 변화가 크다면 무게 중심을 안정적으로 유지하지 못하게 되고, 안전한 고속 주행이 불 가능하며 심한 경우 로봇이 전복될 우려가 있다. 따라서 로봇 몸체의 z축 방향으로의 변위, Roll 방향으로의 각속도, Pitch 방향으로의 각속도 데이터를 FFT 분석을 통해 수식 (2), (3)과 같이 주파수와 진폭의 피크(peak)값에 따른 안정 성을 평가하고자 한다. 또한 각 바퀴의 수직 항력 변화에 따른 불안정성을 나타내는 수식을 정의하여 로봇 모델에 따른 주행 안정성 정도를 평가하고자 한다.
| (1) |
| (2) |
| (3) |
위 식 (1)에서의 X(k)는 몸체 중심의 진동을 FFT로 표 현하기 위한 식이며 k는 주파수를 의미한다. 식 (2), (3)에서 Ia는 FFT의 진폭이 가장 큰 부분의 값을 나타내고 If 는 그 때의 주파수를 의미한다. 그리고 x[n]은 시뮬레이션을 통해 측정된 값을 함수화한 것이며 N은 총 샘플 수 이다.
| (4) |
식 (4)는 각 바퀴의 수직항력 변화에 따른 불안정성을 판단하기 위해 정의된 식으로서 Is 라 정의 하였다. Fis는 안 정적인 상태 즉, 단단한 평지에서 각 바퀴에 걸리는 수직 항력을 의미하고, Fia는 주행에 따라 실시간으로 변하는 각 바퀴의 수직항력을 의미하며, w 은 바퀴의 개수를 의미한 다. 또한 Is 의 값을 무차원화 하기 위해 Fia를 Fis로 나누어 주었다. 일반적으로 무게중심 변화에 따라 수직항력의 변 화가 일어나지만, 서론에 제시된 로봇 메커니즘들은 장애 물을 안정적으로 극복하기 위하여 무게 중심 변화를 완화 해주는 구조로 설계되었다. 따라서 메커니즘에 따라서 수 직항력의 변화가 다르게 나타날 수 있다. 수직항력의 변화 가 크게 나타나는 즉, Is 수치가 크게 나타나는 메커니즘의 경우, 특정바퀴에 무리한 수직항력이 가해지거나, 또는 너 무 작은 수직항력이 가해져 견인력을 상실하게 되는 등의 문제가 발생할 수 있으며, 이 또한 야지 환경에서의 고속 주행을 안정적으로 하기 위한 방해요소가 될 수 있다. 따 라서 FFT 분석결과와, Is 를 비교하여 패시브 타입(Passivetype) 의 메커니즘들만으로 고속 주행 로봇에 적합 가능할 것인가에 대한 여부를 판단하였다.
3. 시뮬레이션 결과 비교 분석
각각의 패시브 타입(Passive-type)의 메커니즘을 분석하기 위하여 ADAMS와 SIMULINK를 연동하여 시뮬레이션 하 였다. ADAMS를 통해 각 로봇 모델과 지형을 설계 하였으 며, 로봇이 주행하면서 장애물과 부딪히는 경우 방향을 잃 지 않게 하기 위하여 SIMULINK를 사용하여 위치제어와 함께 0.5m/s, 1m/s, 2m/s의 3가지의 속도로 시뮬레이션을 해 주었다. 서론에서 언급한 것과 같이, 분석을 위해 선택된 메커니즘들은 모두 저속에서의 안정성을 보장하는 메커니 즘이다.
따라서, 속도를 단계적으로 올려서 시뮬레이션 함으로써 패시브 타입(Passive –type)의 메커니즘으로 주행 가능한 최 대 속도를 확인해보고자 하였다. Table 2에 각 메커니즘 모 델의 시뮬레이션 결과 값을 정리하여 나타내었다. 앞 절에 서 언급한 것과 같이 Ia 와 If 는 FFT의 진폭이 가장 큰 부 분의 주파수 대역과 피크(peak)값을 나타내며, Average Is수 치는 식(4)를 사용한 계산 결과의 평균 값을 나타낸다. 또 한 시뮬레이션 중 로봇이 전복되는 경우는 안정성을 완전 히 잃은 상태라고 분류하여 데이터 분석 표에서는 포함하 지 않았다. 그리고 각각의 메커니즘에 따른 최대 속도를 비교 해본 결과 범퍼 지형1과 범퍼 지형2에서 Basic 모델 이 가장 빠른 주행을 할 수 있었지만, 30°의 경사지형에 서는 매우 저속으로 달려야 했다. 하지만 Crab의 경우 모 든 지형에서 빠른 속도를 유지하면서 달릴 수 있다는 것 을 알 수 있다.
3.1. 로봇 몸체 움직임에 대한 FFT 분석
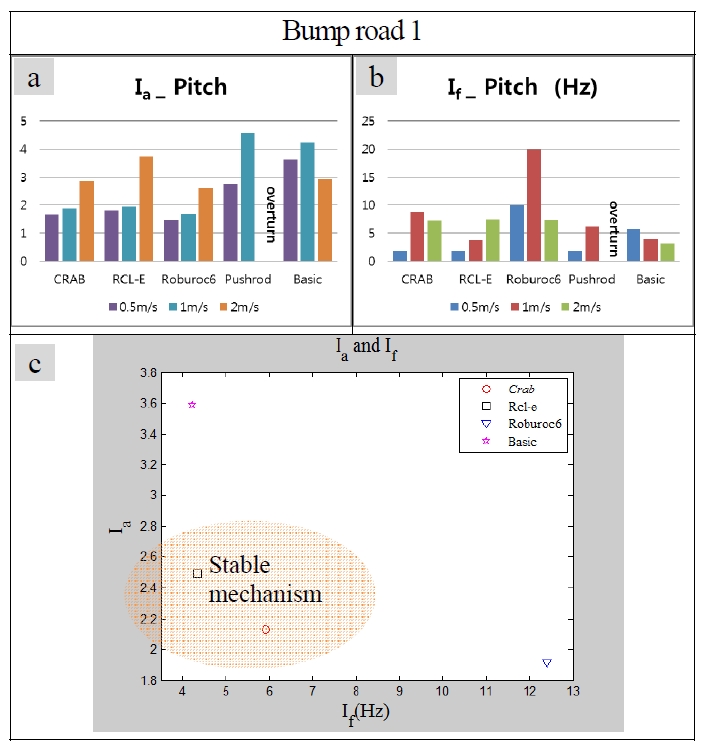
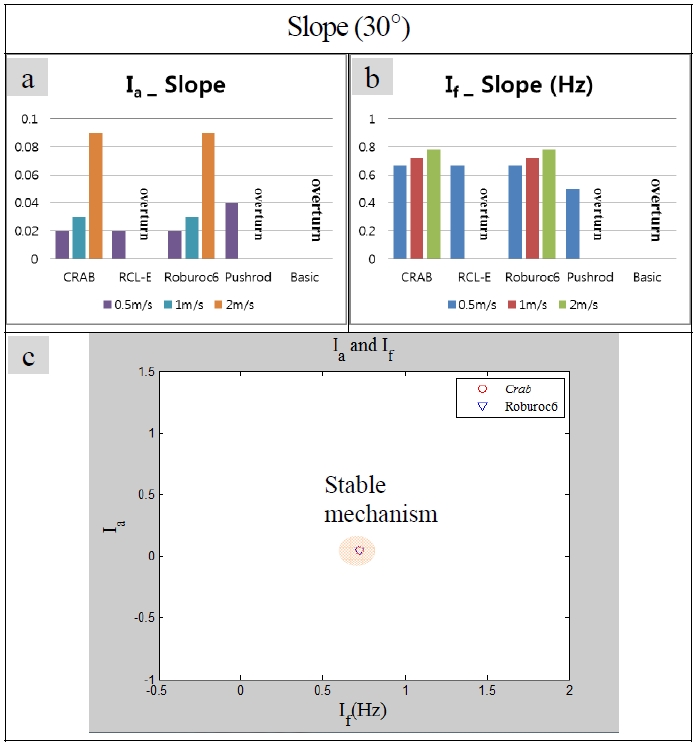
장애물 지형에서 로봇의 주행 안정성을 판단하기 위한 방법으로 FFT 분석을 선택하였다. 먼저 범퍼지형1은 Pitch 방향으로의 안정성 확인하기 위한 지형이므로, FFT 분석을 위해 로봇 몸체의 Pitch 방향으로의 각속도 변화 데이터를 사용하였으며, 범퍼지형2는 Roll 방향으로의 안정성을 확 인하기 위하여 로봇 몸체의 Roll 방향으로의 각속도 변화 데이터를, 마지막으로 Slope 지형에서는 로봇 몸체의 z축 변위 데이터를 사용하였다. Fig. 3 - 5 는 Table 2에 정리한 Ia 값과 If 을 그래프로 나타낸 것이다. 각각의 a, b는 속도에 따른 Ia와 If 값을 표현한 것이고 c는 각 메커니즘 마다 얻 은 Ia의 평균 값과 If의 평균 값을 2차원으로 표현한 그래 프이다. a와 b의 결과 값을 통해 로봇의 속도가 증가할수록 각 지형에서 대체적으로 If값이 증가하는 형태를 나타나고 있는 것으로 속도가 증가함에 따라 진동이 잦아진다는 것 을 알 수 있다.
또한, Ia 값도 대체적으로 증가하는 형태를 보이지만,
모델에 따라서는 속도에 따른 영향을 받지 않는 것도 있음을 확인할 수 있다. 먼저, 범퍼지형1(Bump road1)에서 Roburoc6 의 모델은 1m/s 의 속도일 때 If값이 가장 크게 나타나지만, Ia값을 고려해 볼 때, 불안정성이 많이 증가했 다고 판단하기는 어렵다. 오히려, pushrod suspension 모델의 경우, If값이 Roburoc6 모델에 비해 매우 작게 나타나지만, Ia값을 고려하면 불안정성이 더 높다고 판단할 수 있다. Basic 모델도 pushrod suspension 모델과 마찬가지로 범퍼지 형1에서 If의 값이 낮은 결과를 보이지만, Ia 값이 크게 나 타나는 것으로 보아, 불안정성이 높다고 판단할 수 있다. 따라서 Fig. 3(c) 에서와 같이 Rcl-e 와 Crab이 pitch 방향으 로의 움직임에 대해서는 상당히 안정적이라는 것을 확인 할 수 있었다.
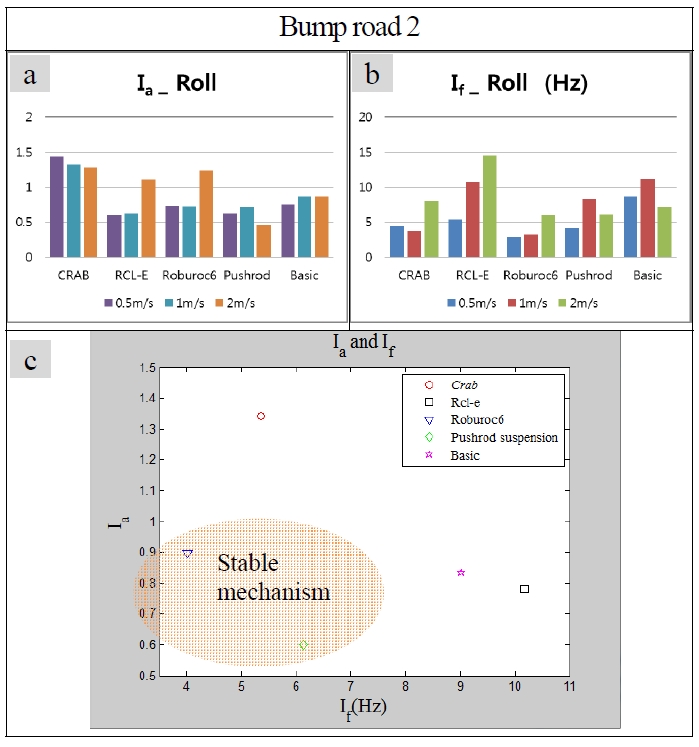
마찬가지로 Fig. 4의 범퍼지형2(Bump road2)에서의 결과 그래프를 볼 때 2m/s에서 Roburoc6의 Ia 값이 가장 크지만 If 값이 낮아 비교적 불안정성이 높지 않다는 것을 알 수 있으며 pushrod suspension 시스템 또한 Ia값과 If의 값이 낮 은 것으로 보아 불안정성이 낮다는 것을 알 수 있다. 따라 서 이러한 결과 값이 Fig. 4 (c)에 나타난 것 과 같이, Roburoc6와 Pushrod suspension이 roll 방향으로의 움직임에 대해서는 비교적 안정적이라는 것을 확인 할 수 있었다.
마지막으로 Fig. 5의 경사지형에서는 Crab과 Roburoc6 만 이 2m/s속력의 주행에도 전복되지 않은 것을 볼 수 있다. 또한 두 모델의 시뮬레이션 결과가 (a), (b), (c)에 나타난 것 같이 비슷한 결과를 보이는 것을 확인 할 수 있다. 따라서 경사진 지형에서는 Crab과 Roburoc6의 메커니즘이 비교적 안정적이라는 것을 확인 할 수 있었다.
3.2. 각 바퀴의 수직항력 변화에 따른 메커니즘의 불안정 성 분석
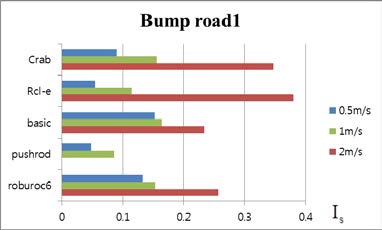
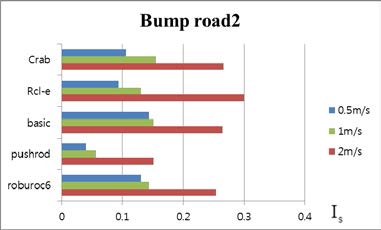
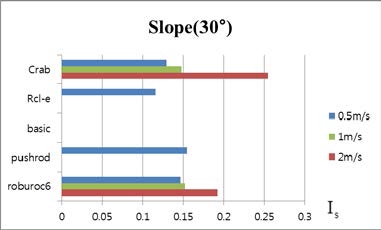
2.3절에서 정의한 식(4)를 바탕으로 실시간으로 얻어진 각각의 모델에 대한 불안정성 정도를 Fig. 6 – 8 에서와 같 이 각 지형과 속도에 따라 평균 값을 비교하였다. 그래프 의 모든 결과는 목표지점까지 전복되지 않고 주행을 완료 한 모델의 데이터를 기반으로 작성되었으며, 시뮬레이션 결과, 로봇이 전복이 된 경우의 데이터는 제외 하였다. 전 체적으로 속도가 증가함에 따라서 장애물 통과 시 각 바 퀴의 수직항력의 변화가 크게 발생하여 불안정성의 수치 가 증가하는 것을 볼 수 있다. 특히, 2m/s의 속력에서는 Is 수치가 급격하게 증가하는 것으로 보아, 고속 주행에서는 다음의 모델들이 안정적인 주행이 불가능 할 것이라는 것 을 예측할 수 있다.
그 중에서도, 범퍼지형1(Bump road1)과 범퍼지형2(Bump road2)의 결과에서 Pushrod suspension 모델이 가장 안정적 인 것으로 나타나지만, 범퍼지형1(Bump road1)의 경우, 2m/s 로 주행 중 전복되는 것을 확인할 수 있었다. 한편, Table 2 에서 나타난 바와 같이 범퍼지형2(Bump road2) 에서는 모 든 모델이 전복되지 않고 장애물을 통과한 것을 확인할 수 있다. 이 중 Pushrod suspension 모델이 FFT 분석결과와 Is 수치상으로 볼 때 가장 안정적인 주행을 한 것으로 판 단할 수 있었는데, 이는 Roll 방향으로의 안정성에 맞춰 설 계된 모델다운 결과라고 생각하였다. 특별히, Crab과 Roburoc6를 제외한 모델들은 경사 지형의 내리막길에서 전복되는 것을 확인할 수 있었는데, Is 수치로 판단할 때, Crab과 Roburoc6는 저속에서 유사한 불안정성을 보이지만 속도가 증가함에 따라 Is 수치가 급격히 증가하는 Crab의 불안정성이 더 커지는 것을 확인할 수 있다. 반면, Fig. 6의 범퍼지형1(Bump road1)에서는 전복된 메커니즘인 pushrod suspension을 제외한 4개의 모델의 Is 평균 값의 변화가 유 사성이 있어 특정 메커니즘이 안정적이라고 판단할 수 없 었다. 마지막으로 Fig. 7의 범퍼지형2(Bump road2)에서는 pushrod suspension의 Is 평균 값이 가장 낮게 나타나는 것으 로 보아 다른 모델에 비해 불안정성이 작다고 판단하였다.
4. 결 론
본 논문에서는 패시브 타입(Passive-type)의 메커니즘들을 설계하여 야지 환경에서의 고속 주행이 가능한지에 대한 여부를 확인하기 위해 ADAMS를 이용하여 시뮬레이션 하 였다.
이를 통해 얻은 결과 값을 평가지표에 맞춰 분석해 보 았고, 각 메커니즘의 장단점을 파악할 수 있었다. 하지만, 야지라는 변수가 많은 환경에서 기존의 패시브타입 (Passive-type) 메커니즘 만으로는 그 변수를 모두 만족시킬 수 없다는 결론을 얻었으며, 고속에서의 안정적인 주행을 위해서는 액티브타입(Active-type)의 구조를 추가로 설계하 거나, 그 외에 안정성을 유지시켜주기 위한 장치 설계가 필요할 것으로 여겨진다.
추후 연구로서는, 본 논문을 통해 얻어진 각 메커니즘들 의 장단점을 적용하여 야지에서의 고속 주행에서도 안정 적으로 장애물을 극복할 수 있는 메커니즘을 설계하고 분 석할 예정이다.
REFERENCES
-
Matsuno, Fumitoshi, Satoshi, Tadokoro, "Rescue robots and systems in Japan", Robotics and Biomimetics, (2004), ROBIO 2004, IEEE International Conference on. IEEE.
[https://doi.org/10.1109/robio.2004.1521744]

-
Kim, J, Lee, J, "Prediction of Maneuverability and Efficiency for a Mobile Robot on Rough Terrain through the development of a Testbed for Analaysis of Robot terrain interaction", Journal of Korea Robotics Society, (2013), 8(2), p116-128.
[https://doi.org/10.7746/jkros.2013.8.2.116]

-
Lee, Woosub, , "Rough terrain negotiable mobile platform with passively adaptive double-tracks and its application to rescue missions", Robotics and Automation, ICRA 2005, (2005), Proceedings of the 2005 IEEE International Conference on. IEEE.
[https://doi.org/10.1109/robot.2005.1570341]

- Kamegawa, Tetsushi, , "Development of the snakelike rescue robot", Robotics and Automation, (2004), 5, Proceedings., ICRA'04. 2004 IEEE International Conference on. IEEE.
- Dongkyu, Choi, Seungmin, Jung, , “The Concept Design of the stable Linkage Mechanism on the Rough Terrain”, (2013), International Conference on Control Automation and Systems, ICCAS.
- Krebs, Ambroise, , "Towards torque control of the CRAB rover", (2008), International Symposium on Artificial Intelligence, Robotics and Automation in Space.
-
Thueer, Thomas, Roland, Siegwart, "Mobility evaluation of wheeled all-terrain robots", Robotics and Autonomous Systems, (2010), 58(5).
[https://doi.org/10.1016/j.robot.2010.01.007]

- Kucherenko, Vladimir, Alexei, Bogatchev, Michel Van, Winnendael, "Chassis concepts for the ExoMars rover", (2004), Proceedings of the 8th ESA Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk, The Netherlands.
- Lucet, Eric, , "RobuROC6: an experimental platform for a high mobility on challenging terrain", Istitut des Systemes Intelligents et de Robotique, Robotics, (2010).
-
Lucet, Eric, , "Dynamic yaw and velocity control of the 6wd skid-steering mobile robot roburoc6 using sliding mode technique", Intelligent Robots and Systems, (2009), IEEE/RSJ International Conference on. IEEE, 2009.
[https://doi.org/10.1109/iros.2009.5354373]

- Yoshimi, Furukawa, Shoichi, Sano, , “REAR SUSPESION FOR VEHICLES”, United States Patent, Patent Number,4,553,768, (1985, Nov).
- Shinji, Kawano, Hiroshi, Tonomura, , “VEHCLE SUSPENSION”, United States Patent, Patent Number, 5,080,389, (1992, Jan).
- Jeffrey Marshall, Lloyd, Auburn, Hills, “SURUT SUSPENSION WITH PIVOTING ROCKER ARM”, United States Patent , Patent no, US 7,185,902 B1, (2007, Mar).
- De Molina, Simon Anne, Stefan, Deferme, "Passive nti-roll system", U.S. Patent No. 6,102,170, (2000, Aug, 15).
- De Molina, Simon Anne, Stefan, Deferme, "Passive anti-roll system", U.S. Patent No. 6,220,406, (2001, Apr, 24).