무인 자동차의 주변 환경 인식을 위한 도시 환경에서의 그래프 기반 물체 분할 방법
†Corresponding author: Electrical Engineering, KAIST, Guseong-dong, Yuseong-gu, Daejeon, Korea ( mjchung@ee.kaist.ac.kr)
© KROS
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In recent years, the research of 3D mapping technique in urban environments obtained by mobile robots equipped with multiple sensors for recognizing the robot’s surroundings is being studied actively. However, the map generated by simple integration of multiple sensors data only gives spatial information to robots. To get a semantic knowledge to help an autonomous mobile robot from the map, the robot has to convert low-level map representations to higher-level ones containing semantic knowledge of a scene. Given a 3D point cloud of an urban scene, this research proposes a method to recognize the objects effectively using 3D graph model for autonomous mobile robots. The proposed method is decomposed into three steps: sequential range data acquisition, normal vector estimation and incremental graph-based segmentation. This method guarantees the both real-time performance and accuracy of recognizing the objects in real urban environments. Also, it can provide plentiful data for classifying the objects. To evaluate a performance of proposed method, computation time and recognition rate of objects are analyzed. Experimental results show that the proposed method has efficiently in understanding the semantic knowledge of an urban environment.
Keywords:
graph-based segmentation, semantic mapping, scene understanding, real-time, urban environment, autonomous vehicle, normal vector estimation, range data.1. 서 론
미국국방고등기획국인 DARPA(Defense Advanced Research Projects Agency)가 2004년 Grand Challenge 대 회를 개최한 이래로, 이동 로봇 또는 무인 자동차의 자율 주행을 위한 연구가 활발히 진행되고 있다[1,2]. 로봇이나 무 인 자동차의 자율 주행을 위해 수행되고 있는 연구들 중에 서 지도 표현(map representation) 혹은 월드모델링(world modeling)이라고도 불리는 주변 환경 모델링에 관한 연구 는 단순히 로봇의 주변 환경에 대한 정보를 제공해줄 뿐만 아니라 로봇의 위치를 추정(localization)하거나 로봇의 주 행 경로를 계획(path planning)하는 연구에도 주로 활용되 고 있다[3,4].
월드모델링을 수행하기 위해서는 로봇의 주변 환경 정 보를 획득할 수 있는 정확하고 정밀한 센서(sensor)들이 필 요하다. 월드모델을 획득하기 위해 사용되는 대표적인 센 서로는 비전 센서(camera), 적외선 센서(TOF camera), 레 이저 거리 측정 센서(LiDAR) 등이 있다.
하지만 이러한 센서를 이용하여 획득한 월드모델의 경 우 로봇이나 무인 자동차에게 단순히 공간 정보만을 제공해 주는 한계가 있다. 따라서 주변 환경의 점유 현상만을 표현 하는 낮은 수준의 지도 표현(low-level map representation) 에서 더 나아가 로봇이 획득한 주변 환경 정보를 이용하여 지형/지물을 인식하고 상황을 판단할 수 있도록 돕는 높은 수준의 지도를 표현(high-level map representation)하는 것 이 로봇의 자율 주행에 있어서 중요하다. 이렇게 의미 있는 정보를 지도에 표현하는 과정을 시맨틱 맵핑(semantic mapping)이라고 한다. 현재 시맨틱 맵핑에 대한 연구는 로 봇 및 컴퓨터 비전 분야에서 활발하게 진행되고 있다[5-8].
J. Strom 외 2인은 레이저 거리 측정 센서와 비전 센서 를 융합한 2차원 정보를 이용하여 실시간으로 물체를 분할 (segmentation)하는 방법을 제안하였다[5]. 이 논문은 레이 저 거리 측정 센서와 비전 센서의 융합을 통해 실시간으로 동작하면서 비교적 정확하게 물체를 분할하는 방법을 제안 하였다. 하지만, 레이저 거리 측정 센서를 통해 획득한 3차 원 정보를 2차원 정보로 변환하는 과정에서 정보의 손실이 발생하고, 비전 센서의 경우 조경 변화에 민감하므로 조경 변화가 다양한 실외 환경의 경우 한 물체 내에서 여러 개의 물체로 분할되는 과분할(over-segmentation) 현상이 나타 나 물체 분할의 정확성이 떨어진다.
H. Zhao 외 7인은 2차원 레이저 거리 측정 센서를 차량 의 양쪽 측면에 수직으로 설치하여 차량이 이동함에 따라 연속적으로 거리 정보를 획득할 수 있는 센서 시스템을 구 성하였다[6,7]. 이러한 방식을 통해 획득한 거리 정보를 이용 하여 2차원 거리 영상(range image)을 획득할 수 있다. 이 를 영상 기반 물체 분할 알고리즘에 적용하여 물체를 효과 적으로 분할(segmentation)하고 분류(classification)하는 방법을 제안하였다. 이 논문은 높은 물체 분류의 정확성을 보여주지만 실시간으로 동작할 수 없으므로 실제 무인 자 동차에 적용하기에는 한계가 있다.
A. Golovinskiy 외 2인은 레이저 거리 측정 센서를 이 용하여 획득한 3차원 점군(point cloud)에 대하여 물체를 분할하는 방법을 소개하였다[8]. 이 논문에서는 물체를 정확 하게 분할하기 위하여 Min-cut 알고리즘으로 전경과 배경 을 분할한다. 이 때, 군집화된 점들에 대해 점의 수, 군집 영역의 부피, 점군의 평균 높이 그리고 높이의 표준 편차 등을 특징으로 하는 특징점(saliency feature)을 기준으로 물체를 구분한다. 이 논문은 3차원 정보를 이용하여 물체 분할을 수행하였으나, 물체를 분할하는데 15시간이 소요되 어 실시간성을 보장하지 못한다.
지금까지 살펴본 기존 연구들은 높은 인식률 확보에 초 점을 두거나 실시간성 확보에 초점을 두었다. 하지만, 인식 률과 실시간성을 동시에 고려하는 연구는 많지 않았다. 그 이유는 실시간성 확보와 높은 인식률을 동시에 보장하기가 쉽지 않고, 처리되는 정보의 형태에 따라서 처리 속도 및 인식률의 개선에 대한 접근 방식이 달라지기 때문이다. 하 지만, 로봇이나 자율 주행 차량에 적용하기 위해서는 주변 환경 정보를 가지고 있는 정교한 월드모델이 필요하고, 이 를 위해 다른 센서들에 비해 빠르고 정확한 레이저 센서를 통해 획득한 3차원 정보를 이용하여 높은 주변 환경 인식 률을 보장하고 정보를 획득함과 동시에 처리가 가능한 실 시간 알고리즘이 필요하다.
본 논문의 목표는 무인 자동차의 자율 주행을 위하여 도시 환경에서의 주변 환경 정보를 실시간으로 인식하는 방법을 제안하는 것이다. 이를 위하여 센서를 통해서 획득 한 연속적인 거리 정보를 이용하는 방법과 그래프 모델을 이용하여 물체를 정확하고 효과적으로 분할하는 방법을 제 안한다.
2. 도시 환경에서의 그래프 기반 물체 분할 방법
2.1. LiDAR를 이용한 연속적인 거리 정보 획득
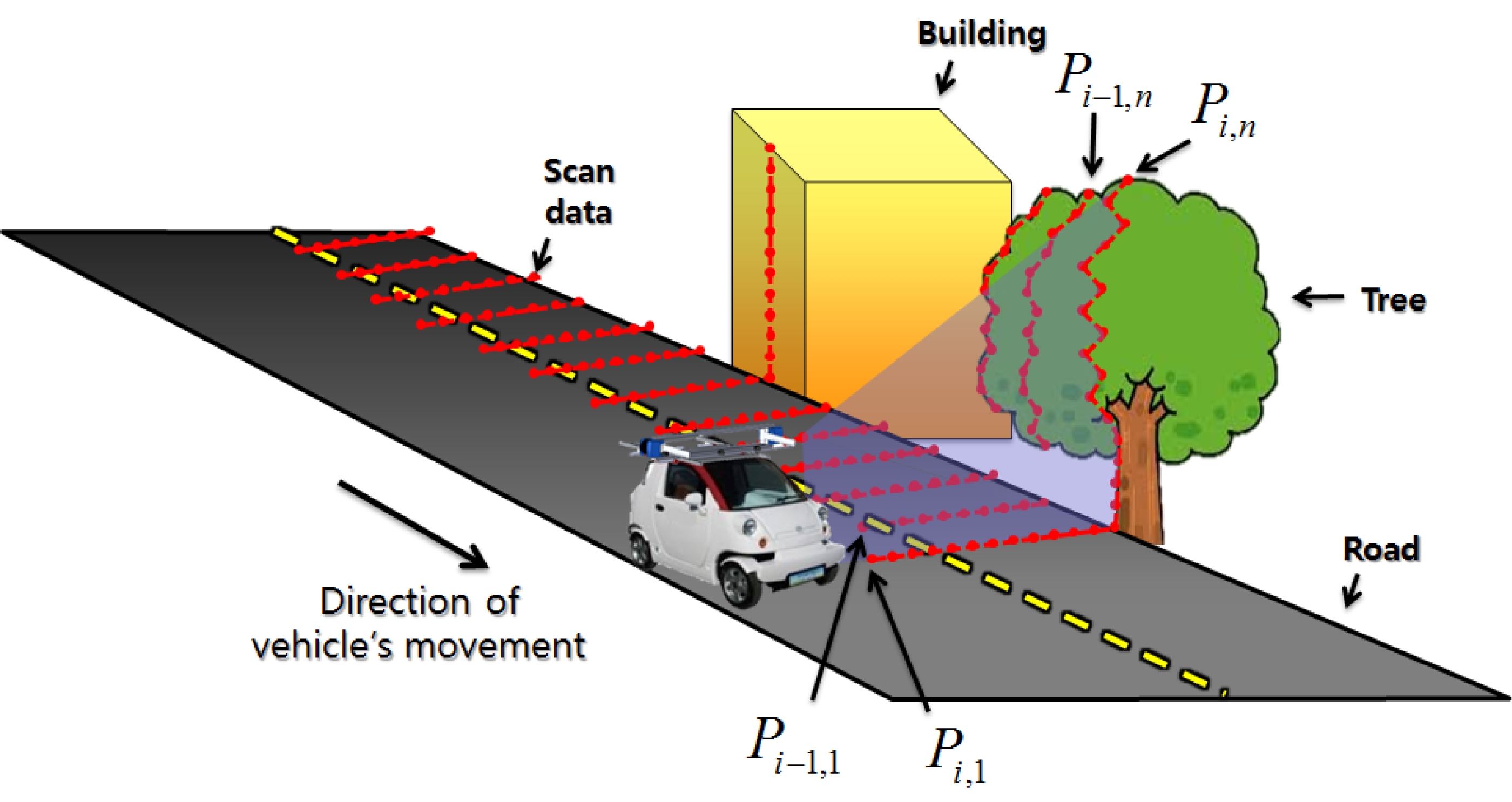
2차원 레이저 거리 측정 센서(LiDAR)를 이용하여 월 드 모델을 생성하기 위한 기존의 센서 시스템의 경우 2차 원 레이저 거리 측정 센서를 센서 시스템 측면에 수직으로 설치하였다[6,7,9,10]. 2차원 레이저 거리 측정 센서를 시스템 측면에 수직으로 설치하면 차량이 이동하면서 2차원 레이 저 거리 측정 센서가 수직으로 주변 환경을 스캔하게 된다. 그렇게 되면 주행 중에 연속적으로 수직으로 스캔한 정보 가 축적되게 되고, 그것을 이용하여 주변 환경 정보가 포함 된 3차원 점군을 쉽게 획득할 수 있게 된다.
Fig. 1은 LiDAR를 차량에 수직으로 설치한 센서 시스 템을 이용하여 연속적인 거리 정보 획득을 하는 과정을 나타 낸다. 여기서 LiDAR를 통해 i번째로 스캔된 정보를 Pi라 하고, i번째 스캔 정보 중에서 k번째에 측정된 점을 pi,k라고 한다. 즉, i번째 스캔 정보 중 측정된 점의 개수가 총 n개라 면 스캔 정보 Pi 는 Pi = {Pi,1,...Pi,n} 로 표현될 수 있다. 획득된 거리 정보는 3차원 점군을 형성하는데 이용된다.
2.2. 주변점(neighbor)의 검색
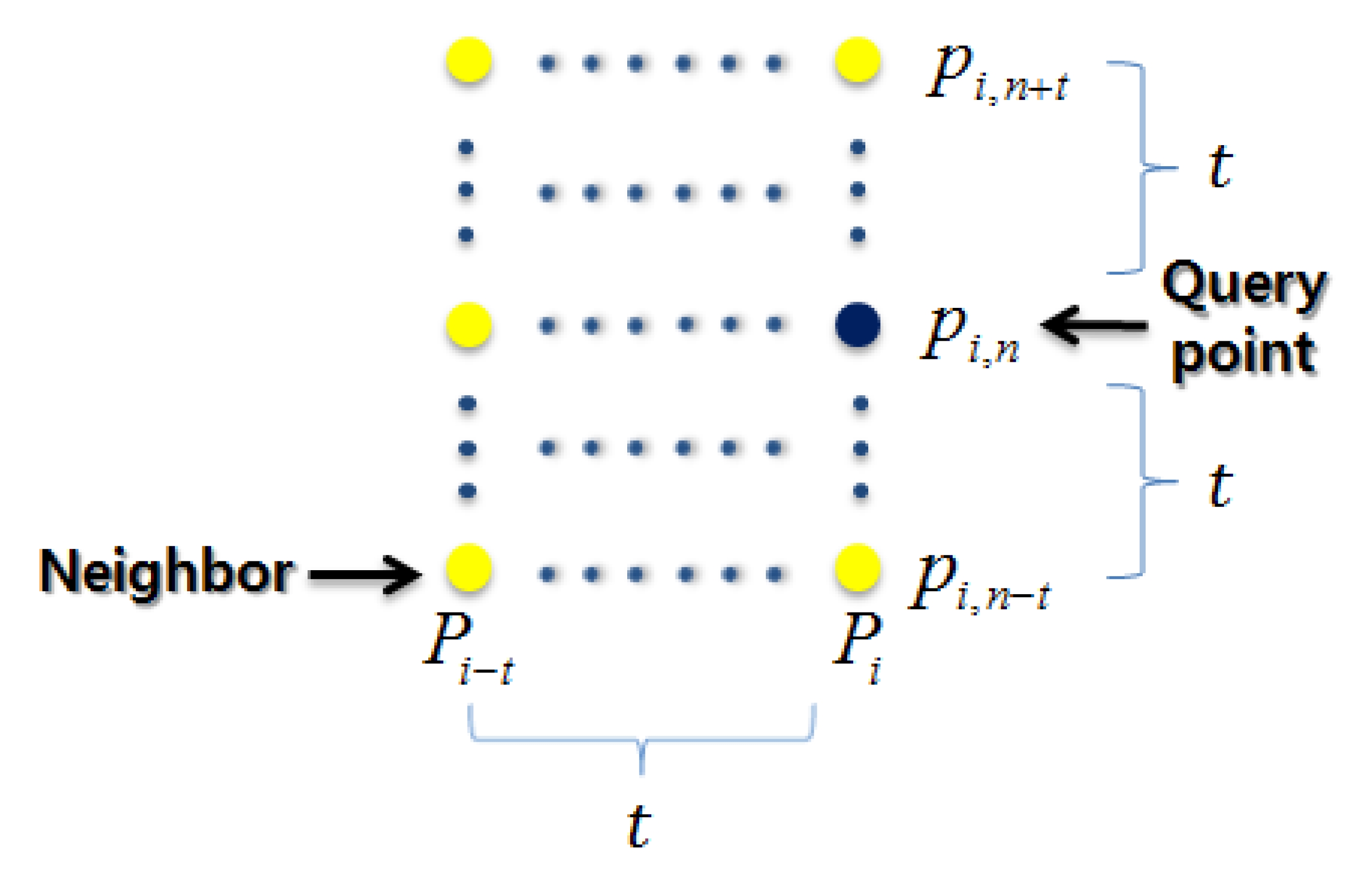
주변 환경을 정확하게 인식하기 위해서는 3차원 점군 내에서 물체로 추정되는 부분을 정확하게 분할하는 과정이 필요하다. 이를 위해서는 조사 영역(window)을 설정하고, 조사 영역 내의 점들 사이의 관계를 조사하여 물체로 추정 되는 부분을 올바르게 가려낼 수 있어야 한다. 3차원 점군 내의 물체를 효과적으로 분할하기 위해서 일반적으로 조사 점(query point)으로부터 거리가 가까운 주변점(neighbor) 을 찾은 후, 조사점과 주변점 사이의 관계를 이용하여 점들 을 하나의 객체로 묶어나가는 클러스터링(clustering) 방법 이 이용된다[11].
2.1절에서 설명했듯이 LiDAR를 수직으로 설치한 센서 시스템을 통해 획득한 3차원 점군은 연속적으로 생성되는 스캔 정보의 특성 때문에 이전의 스캔 정보를 확인하기 편 리하고, 쉽게 접근 가능하다. 따라서 실시간으로 생성되고 있는 스캔 정보와 연속적으로 축적된 이전 스캔 정보 사이 의 관계를 이용하면 점군 내에서 물체로 추정되는 범위를 효과적으로 분할할 수 있다. 본 논문에서는 Fig. 2와 같이 실시간으로 주변점을 검색하기 위하여 연속적인 레이저 스 캔 정보에 대하여 현재와 과거의 스캔 정보만을 이용한다. 또한, 주변점을 효과적으로 검색하기 위하여 조사 영역을 이용하고, 스캔 정보의 성김이나 조밀함의 정도, 환경의 복 잡도 등에 따라 사용될 주변점의 개수는 달라져야한다는 사실을 고려하여 조사 영역의 크기를 가변적으로 조절하여 상황에 따라 유동적으로 주변점의 개수를 설정할 수 있도 록 하였다. 조사 영역 크기에 따른 주변점의 개수는 수식 (1)에 의해 결정된다.
Relationship between the window and the neighbors (Blue indicates the query point and yellow indicate the neighbors)
| (1) |
여기서 t는 조사 영역 조절 변수로 t에 따라 주변점의 개수 인 k가 결정된다. 예를 들어, t = 2일 경우 결정되는 주변 점은 14개가 되어 14-NN으로 물체 분할을 수행한다는 의 미가 된다. 결정된 주변점은 2.3절에서 소개될 법선 벡터의 추정 과정과 2.4절에서 소개될 물체 분할 과정에 이용된다.
2.3. 법선 벡터(normal vector)의 추정
3차원 점군 내의 물체의 영역을 추정하기 위하여 본 논 문에서는 점들 사이의 거리 관계를 나타내는 유클리디안 거리(Euclidean distance)와 점들 사이의 각도 관계를 나타 내는 법선 벡터(normal vector)를 이용하여 물체를 분할 과 정을 수행한다. 이러한 관계를 이용하여 물체 분할 수행 과 정을 설명하기 이전에 점들 사이의 각도 관계를 나타내는 법선 벡터를 추정하는 과정에 대하여 설명한다. 법선 벡터 는 주로 평면의 주성분분석(Principal Component Analysis : PCA)을 통하여 쉽고 빠르게 추정할 수 있다[12]. 본 논문 에서는 2.2절에서 결정된 조사점과 주변점들을 이용하여 평면을 결정하여 법선 벡터를 추정한다.
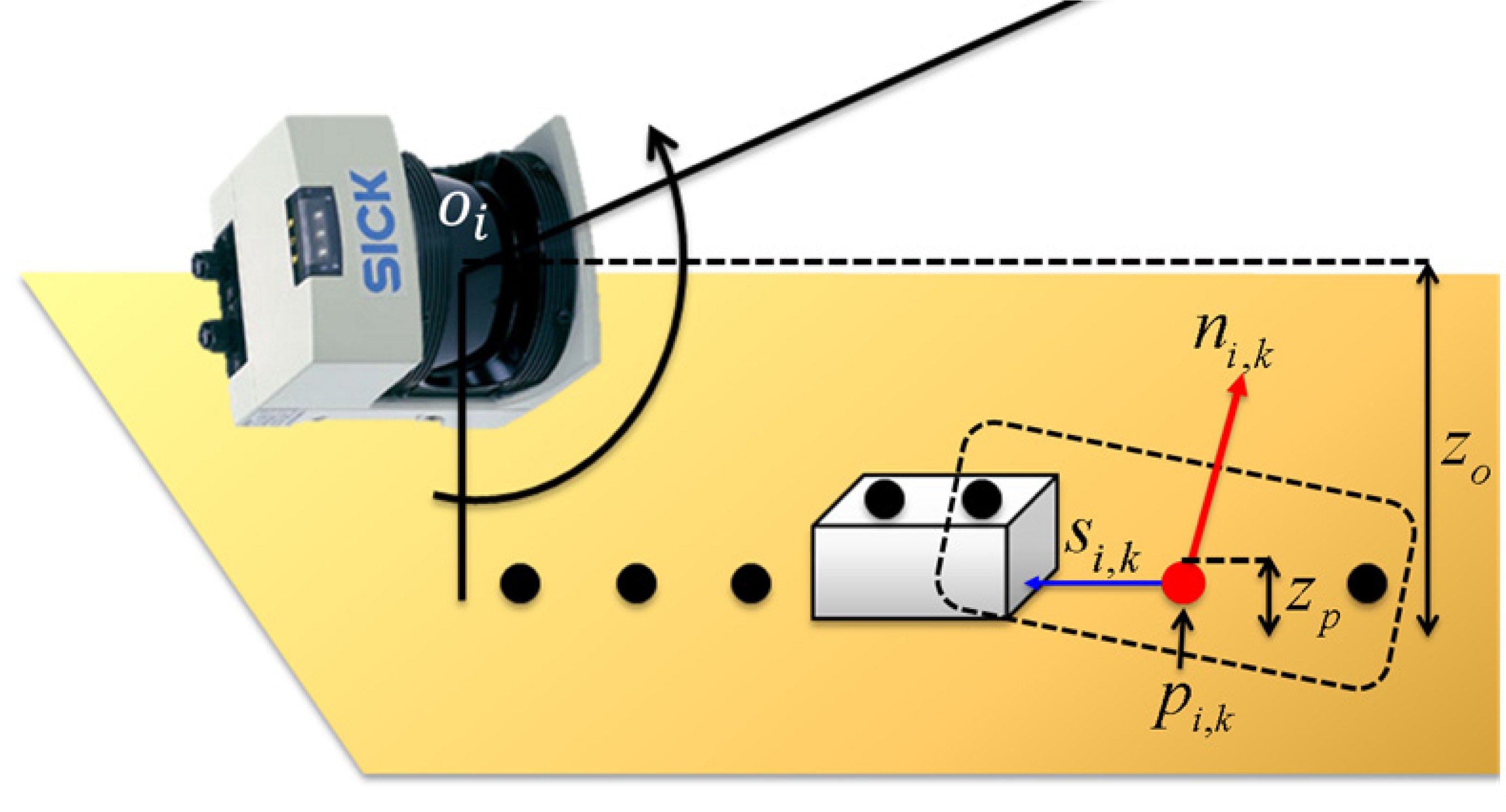
하지만 이렇게 추정된 법선 벡터의 방향은 유일하지 않 다. 그 이유는 한 평면에 대하여 추정될 수 있는 법선 벡터 는 두 가지가 존재하기 때문이다. 만일 벡터의 방향이 잘못 추정되어 동일한 평면에 위치한 이전 벡터 방향과의 각도 의 차이가 클 경우, 동일한 평면에 위치함에도 다른 평면으 로 위치하는 것으로 인식될 수 있다. 본 논문에서는 추정된 법선 벡터의 방향을 일관적으로 보정하기 위하여 센서의 위치를 고려하였다. 센서의 위치를 고려할 수 있는 근거는 스캔된 점들은 스캔이 이루어질 당시의 고정된 위치를 가 진 센서에 의해 공통적으로 생성되기 때문이다. 따라서 생 성된 모든 점에 대해서 센서의 위치는 일관적이므로 벡터 의 방향을 보정할 기준이 되기에 충분하다. i번째 스캔 정 보의 k번째 점인 pi,k = (xp,yp,zp) 가 조사점일 경우 추정 된 법선 벡터는 ni,k라 정의될 수 있고, i번째 센서의 위치 를 oi = (xo,yo,zo)라 정의될 수 있다. 이때의 벡터 방향의 보정 과정은 수식 (2)에 결정된다.
| (2) |
여기서 si,k는 ni,j 의 방향을 보정하기 위하여 센서의 위치 정보가 포함된 비교 벡터로 수식 (3)과 같이 정의된다.
| (3) |
수식 (2)에서 확인할 수 있듯이 법선 벡터 방향은 ni,j 와 si,k의 내적(inner product)의 결과로 확인할 수 있는 부 호(sign)의 변화에 의해 결정된다. si,k의 방향은 센서를 향 하는 방향이므로 ni,j의 방향이 센서를 향하는 방향이 아니 라면 내적의 결과가 음이 되므로 ni,j의 부호를 바꾸게 된 다. 또한 제안한 방법은 스캔된 점의 높이가 센서의 높이보 다 낮을 경우 내적의 결과를 반영하지 않는다. 그 근거는 센서의 높이보다 높은 물체의 경우(zp > zo) 가려지는 영 역이 발생하여 물체의 뒤의 영역이 스캔되지 않으나, 센서 의 높이보다 낮은 물체가 존재할 경우(zp < zo) 물체 뒤의 영역이 스캔되어 Fig. 3과 같이 내적의 결과가 음이 되는 경우가 발생한다. 이와 같은 경우를 제외하고 내적의 결과 를 벡터 추정 결과에 적용함으로써 최종적으로 벡터의 방 향을 보정하게 된다.
2.4. 점진적 그래프 기반 물체 분할 방법
컴퓨터 그래픽스 분야에서는 영상 내에서 물체로 추정 되는 영역을 구분하기 위하여 그래프 모델을 이용한 영상 분할(image segmentation)에 관한 연구를 활발히 진행해왔 다[13]. 그래프 모델을 이용한 영상 분할 방법을 뜻하는 그래 프 기반 분할 방법(graph-based segmentation)은 최적의 해 를 구하기 위한 많은 반복적인(iterative) 연산을 수행하기 때문에 비교적 정확한 영상 분할 결과를 제공해준다. 하지 만 이를 3차원 정보에 적용할 경우 많은 정보의 양과 반복 적인 연산 때문에 많은 연산 시간이 소요된다. 따라서 3차 원 정보를 이용하여 실시간성과 높은 물체 분할 성능을 동 시에 보장하기 위해서는 기존 방법의 변화가 필요하다.
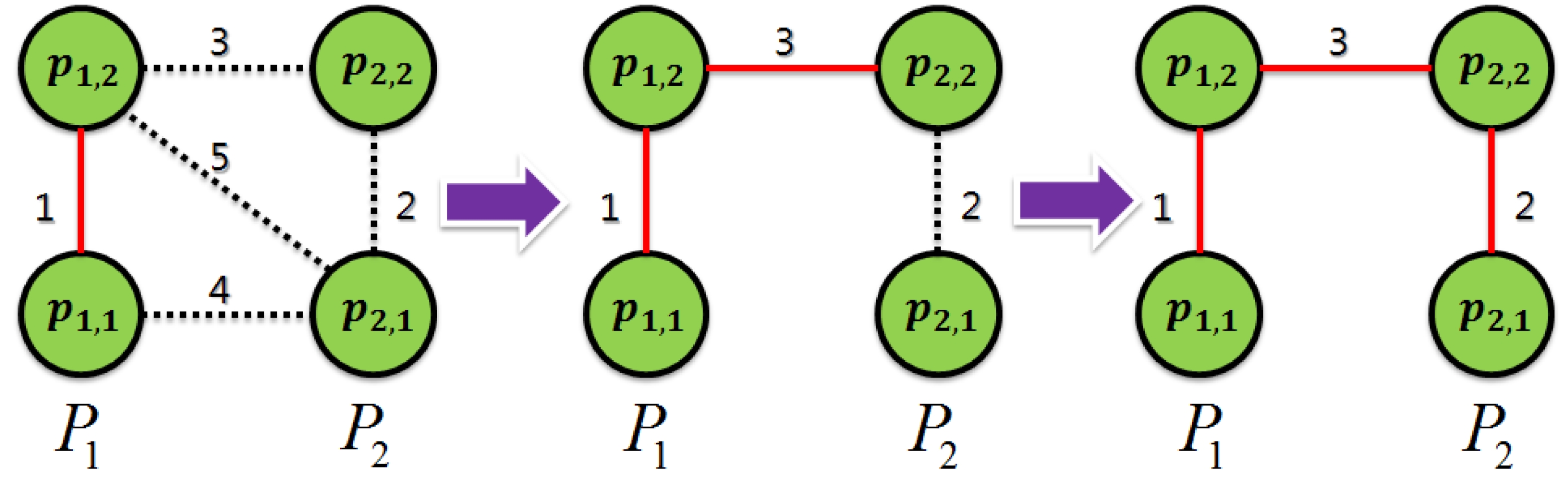
본 논문에서는 [13]의 영상 분할 방법을 참고하여 2.1 절에서 설명한 연속적으로 들어오는 3차원 스캔 정보에 대 하여 실시간성과 높은 물체 분할 성능을 동시에 보장하는 점진적(incremental) 그래프 기반 물체 분할 방법을 제안한 다. 제안하는 방법이 그래프 기반 분할 방법임에도 빠르고 정확한 분할 결과를 획득할 수 있는 이유는 연속적인 3차 원 정보에 대해서 점진적으로 최소 신장 트리(Minimum Spanning Tree : MST)를 찾아나감으로써 물체를 분할해 나가기 때문이다. 최소 신장 트리는 모든 점들을 에지 (edge)로 연결한 신장 트리(spanning tree) 구조 중 에지의 가중치(weight)의 합이 최소가 되는 신장 트리를 의미한다. 에지의 가중치의 합이 최소가 되는 트리가 물체 분할 결과 에 적용될 수 있는 근거는 한 물체에 속해 있는 점들은 점 과 점 사이의 거리가 가깝거나 벡터의 방향이 유사한 것처 럼 서로 비슷한 특성을 가지는데 특성이 유사할수록 에지 의 가중치의 값을 낮추어 최소 신장 트리를 적용 가능하도 록 설정할 수 있기 때문이다.
최소 신장 트리는 점진적으로 들어오는 스캔 정보에 대 해서 복잡한 연산 과정 없이 빠르게 형성해나갈 수 있다. Fig. 4와 같이 P1 의 결과에서 점진적으로 스캔 정보 P2 가 추가적으로 측정될 경우 이전 점들과 생성된 점 사이의 에 지와 에지의 가중치를 빠르게 설정해 나갈 수 있다면, 에지 들 중 최소의 가중치를 갖는 에지만을 선택해 나감으로써 최소 신장 트리를 빠르게 형성해나갈 수 있다.
2.4.1절에서 설명한 최소 신장 트리를 형성하기 위해서 는 먼저 에지의 가중치(weight)를 정의하여야 한다. 일반적 으로 가중치는 점과 점 사이의 관계를 나타내는 요소로 정 의하는데 본 논문에서는 2.2절에서 설명한 조사점과 주변 점의 관계를 통하여 구할 수 있는 점과 점 사이의 거리 유 사성(point distance similarity)과 2.3절에서 설명한 법선 벡터의 유사성(normal vector similarity)을 조합하여 사용 한다. 점과 점 사이의 거리 유사성과 법선 벡터의 유사성은 수식 (4), 수식 (5)와 같이 각각 정의된다.
| (4) |
| (5) |
수식 (4)에서 υ는 2.2절에서 획득한 조사 영역 내의 3차 원 점을 의미하고, rmax 는 레이저 거리 측정 센서가 제공하 는 거리 정보의 최댓값으로 거리의 유사성을 나타내는 변수 인 ρd를 정규화(normalization)하기 위해 사용되었다. 수식 (5)에서 n은 υ에 해당하는 법선 벡터를 의미한다. 법선 벡 터의 유사성을 나타내는 변수인 ρn 또한 0과 1사이의 값을 갖는다. ρd와 ρn의 값이 작을수록 두 점은 높은 유사도를 나타내고, 값이 클수록 두 점은 낮은 유사도를 나타낸다.
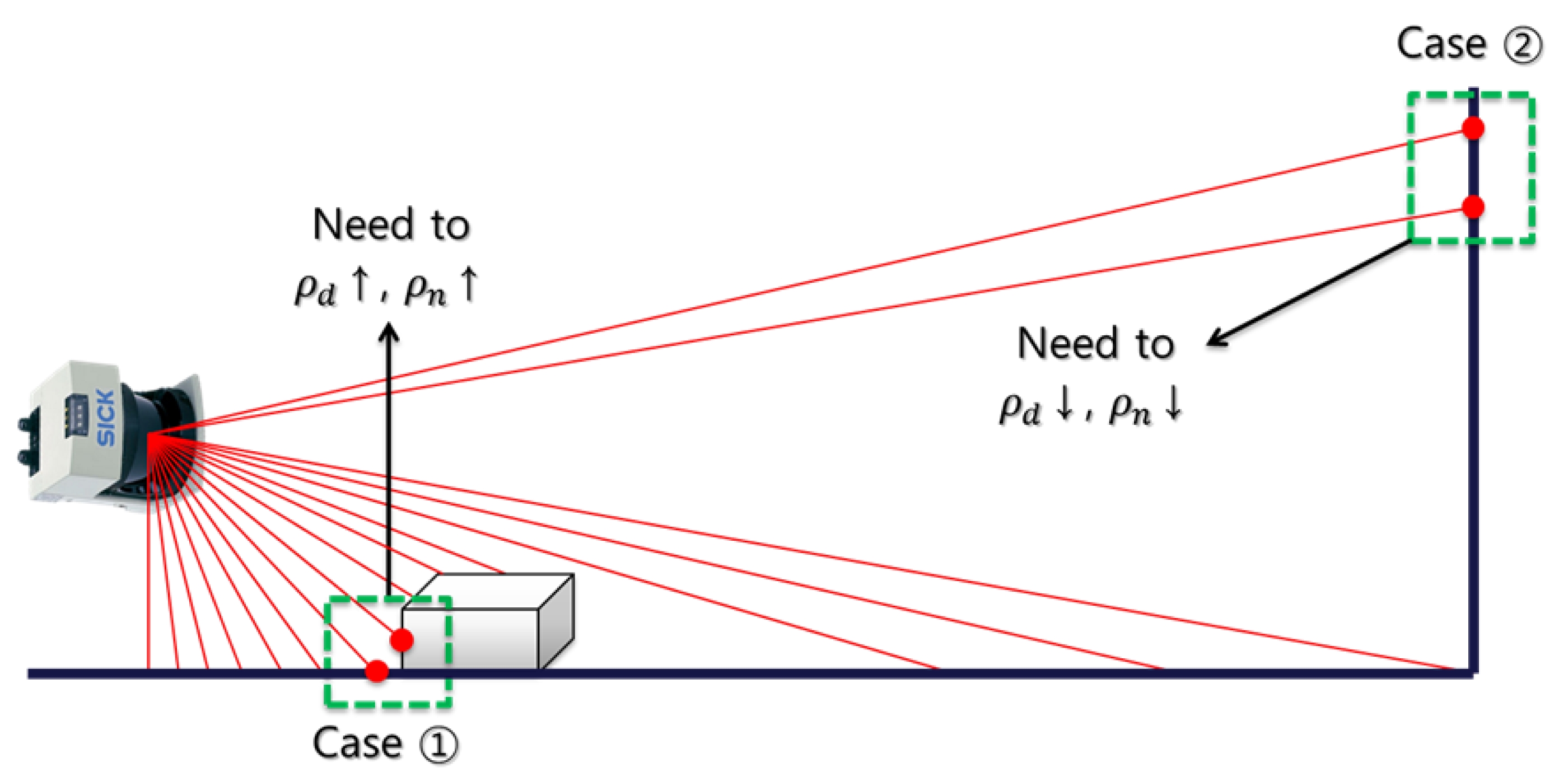
이렇게 정의한 ρd와 ρn을 조합하여 가중치 함수 (weight cost function)를 정의하여 가중치를 결정하기 전 에 추가적으로 고려해야 할 것은 거리 정보이다. 그 까닭은 도시 환경의 경우 측정거리가 수십 미터로 범위가 넓고, 센 서의 측정 거리가 멀어지면 멀어질수록 점과 점 사이의 거 리가 점점 멀어지기 때문이다. 예를 들어, Fig. 5의 경우 (Case) ➀에서는 센서의 측정거리가 가까우므로 두 점 사 이의 거리가 가깝게 측정될 것이다. 그렇기 때문에 ρd와 ρn의 값이 작게 도출될 수 있다. 이는 두 점이 각각 다른 물체에 속해 있으나 유사성이 높으므로 한 물체로 인식하 는 문제를 유발한다(over-segmentation). 따라서 거리 정보 를 이용하여 ρd 와 ρn의 값을 높임으로써 다른 물체로 인식 할 수 있도록 해야 한다. Fig. 5의 경우(Case) ➁에서는 센 서의 측정거리가 멀므로 두 점 사이의 거리가 멀게 측정될 것이다. 그렇기 때문에 ρd 와 ρn의 값이 크게 도출될 수 있 다. 이는 두 점이 같은 물체에 속해 있으나 유사성이 낮으 므로 다른 물체로 인식하는 문제를 유발한다(under-segmentation). 따라서 거리 정보를 이용하여 ρd와 ρn의 값을 낮춤으로써 같은 물체로 인식할 수 있도록 해야 한다.
이렇게 정의한 ρd와 ρn, 그리고 거리 정보를 조합하여 가중치 함수를 정의하여 가중치를 구한 후, 그것을 각 에지 에 할당한다. 가중치 함수는 수식 (6)과 같이 정의된다. 여기서 ri는 i번째 점에서의 센서 측정 거리이고. wij는 i와 j번째 점 사이에 연결된 에지의 가중치이다. 그리고 ks는 ρd와 ρn의 효과를 조절하기 위한 상수를 나타낸다. ks는 ρd와 ρn의 효과를 조절할 수 있으므로 ρd와 ρn의 값에 따라 물체들을 합칠지(merge) 혹은 나눌지(separate)를 결 정할 수 있게 된다. 따라서 ks의 조절을 통해 보다 나은 물체 분할 효과를 볼 수 있다. ks의 설정에 대한 자세한 내용은 4장에서 자세히 다룬다. 또한 거리 정보를 가중치에 반영함으로써 거리가 가까울수록 ρd와 ρn을 높여 Fig. 5의 경우 ➀의 문제를 피할 수 있고, 거리가 멀수록 ρd와 ρn을 높여 Fig. 5의 경우 ➁의 문제를 피할 수 있도록 하였다.
| (6) |
2.4.2절에서 구한 가중치의 함수를 이용하여 물체 분할 을 결정하기 위해서 본 논문에서는 [13]의 분할 척도 (segmentation measure)를 물체 분할 과정에 이용한다. 첫 번째는 클러스터 내부 결합력(Internal difference : Int)으 로 수식 (7)과 같이 정의된다.
| (7) |
여기서 C는 클러스터, e는 에지 그리고 MST는 최소 신장 트리를 의미한다.
두 번째는 클러스터 간의 결합력(Difference between two clusters : Dif)으로 수식 (8)과 같이 정의된다.
| (8) |
여기서 C는 클러스터, E는 에지의 집합을 의미한다.
앞서 설명한 두 분할 척도를 이용하여 최종적으로 클러 스터간의 결합 혹은 분할을 결정(segmentation decision)한 다. 클러스터의 결합 과정과 분할 과정은 수식 (9)와 수식 (10)에 의하여 각각 결정된다.
| (9) |
| (10) |
수식 (9),(10)에서 MInt(C1,C2)는 최소 클러스터 내 부 결합력(Minimum Internal difference)으로 클러스터 C1과 C2의 클러스터 내부 결합력 값들 중 최솟값으로 수 식 (11)과 같이 정의된다.
| (11) |
수식 (11)에서 τ(C)는 임계 함수(threshold function) 이다. τ(C)를 도입한 이유는 한 점으로 구성된 클러스터 일 경우 최소 신장 트리로 구성되지 않아 가중치의 값이 정의되지 않게 된다. 따라서 이와 같은 클러스터는 물체 분 할 과정에 적용할 수 없으므로 τ(C)를 적용하여 정량적인 값을 갖도록 하고, 물체 분할 과정에 적용될 수 있도록 한 다. τ(C)는 수식 (12)와 같이 정의된다.
| (12) |
앞서 설명한 내용들을 바탕으로 실제 3차원 점군에 적 용했을 경우 점진적 그래프 기반 물체 분할 방법의 수행 과정을 요약하면 다음과 같다.
- LiDAR를 이용한 스캔 정보(Pi) 획득
- 주변점의 검색을 이용하여 에지를 생성
- 생성된 에지의 가중치를 결정
- 생성된 모든 에지에 대해서 에지의 가중치 값에 따라 오름차순으로 정렬
- 스캔을 통하여 획득한 각각의 점(pi,k)에 대한 클러스터 생성
- 가중치 값을 정렬한 순서대로 분할 척도에 따른 물체 분할 결정
- 생성된 모든 에지에 대하여 ➅을 반복
제안한 방법은 무인 자동차의 자율 주행을 위해 분할된 물체의 3차원 특징 정보(feature)를 제공한다(Table 1). Table 1에서 ƒ1 ~ ƒ7은 객체 단위로 추출한 특징점(object level features)에 해당되고, ƒ8 ~ ƒ10 점 단위로 추출한 특 징점(point level features)에 해당된다.
3. 실험결과 및 분석
3장에서는 도시 환경에서의 3차원 점군을 얻기 위하여 실험에 사용된 센서 시스템에 대해 설명하고, 센서 시스템 을 통해 획득한 데이터를 제안한 방법에 적용하여 획득한 실험 결과와 결과에 대한 분석에 대하여 설명한다.
3.1. 센서 시스템 및 실험 데이터
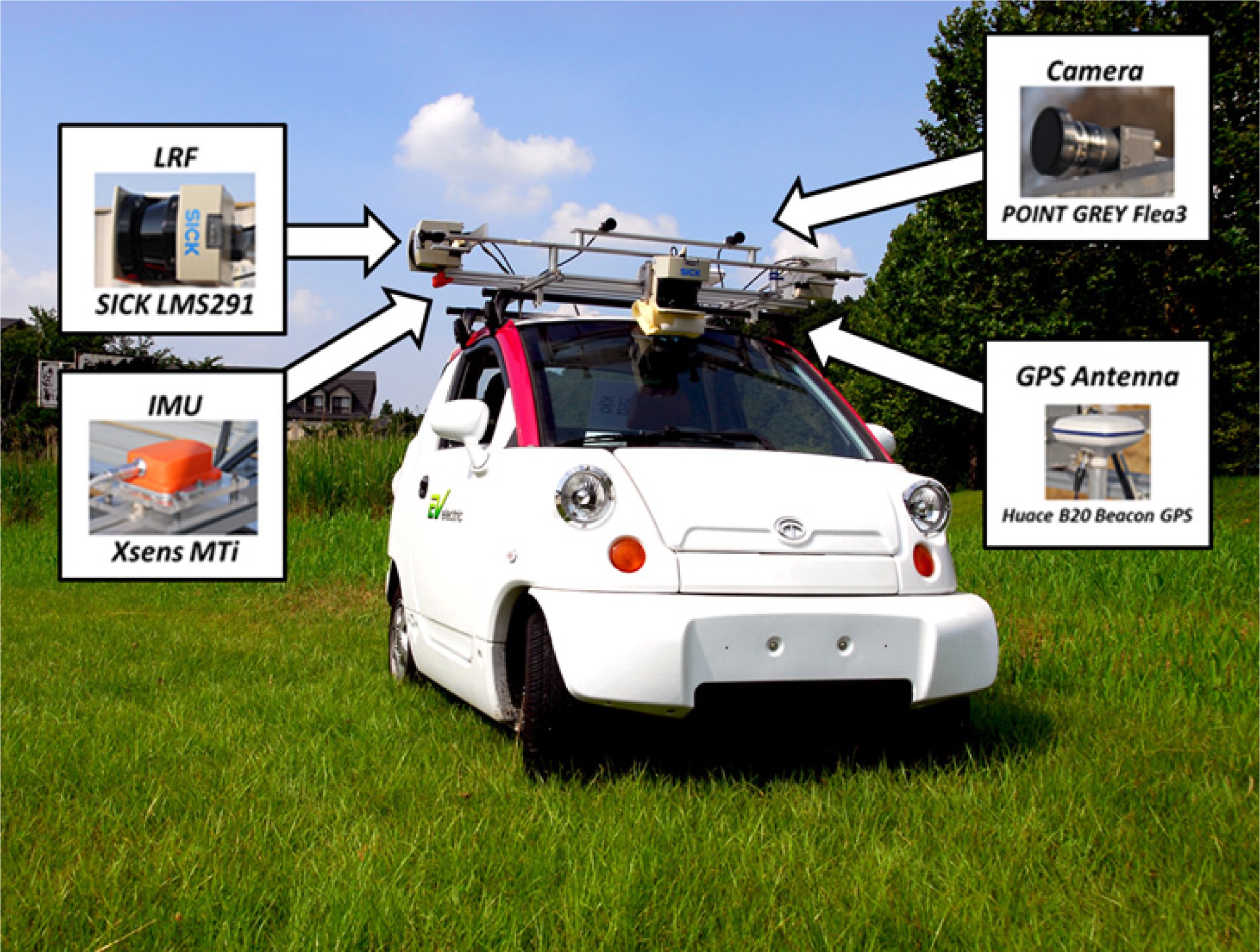
Fig. 6은 실험을 위해 사용된 센서 시스템을 나타낸다. 전방에는 레이저 거리 측정 센서 1대와 스테레오 카메라 1대, 좌/우측에는 레이저 거리 측정 센서와 카메라가 각각 1대씩 설치되어 있으며, 차량의 위치 정보는 GPS와 IMU 를 통하여 획득할 수 있다. 본 실험에서는 좌/우측에 설치 된 레이저 거리 측정 센서만을 이용하였다. Table 2는 실험 에 사용된 센서 시스템의 주요 사양을 나타낸다.
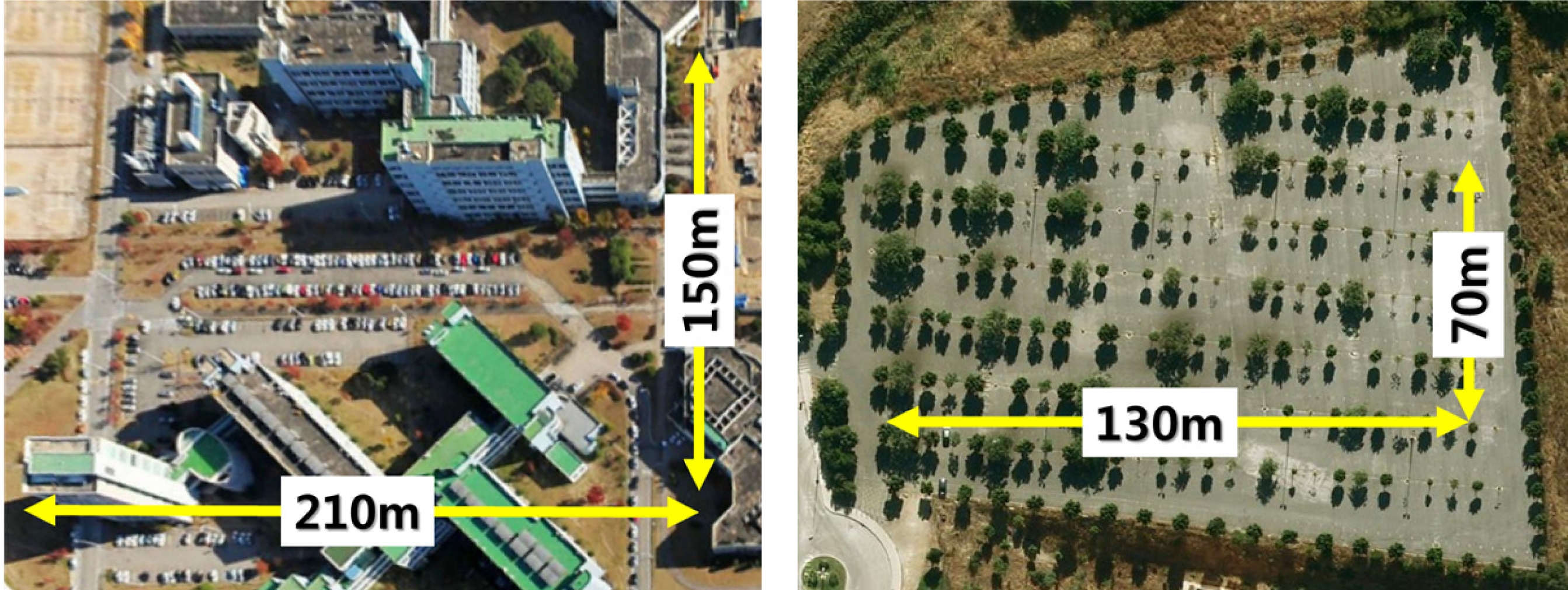
Fig. 7은 실험 데이터를 획득한 실험 환경을 나타낸다. Fig. 7의 왼쪽은 KAIST 캠퍼스 실험 환경으로 Fig. 6의 센서 시스템을 이용하여 실험 환경을 주행한 후 실험 데이 터를 획득하였다. KAIST 캠퍼스 실험 환경은 다양한 크기 의 건물들이 존재하고 주변에 나무가 많음은 물론, 주차장 이 존재하여 다양한 종류의 차들이 존재하므로 제안한 방 법의 성능을 쉽게 확인하기 용이하다. 실험 차량은 10~15km/h의 속력으로 주행하였으며, 총 1,214,443개의 점군을 획득하였다. 추가적으로, 제안한 방법이 다른 실험 환경에도 잘 적용됨을 확인하기 위하여 Fig. 7 오른쪽의 Málaga 캠퍼스 주차장 환경의 공개된 데이터 세트[14]를 이 용하여 제안한 방법에 적용하였다. 획득된 점군의 수는 총 630,904개이다.
3.2. 실험 결과
Fig. 8과 Fig. 9는 KAIST 캠퍼스와 Málaga 캠퍼스 주 차장 환경에서 획득한 데이터를 이용하여 제안한 방법을 적용한 결과를 나타낸다. Fig. 8과 Fig. 9에서 가운데 표시 된 노란선은 차량의 주행경로를 의미하며, 물체 분할의 결 과를 쉽게 확인할 수 있도록 분할된 각각의 물체들은 서로 다른 색깔로 표시하였다. 결과에서 확인할 수 있듯이 제안 한 방법이 차량이 주행함에 따라 점진적으로 들어오는 스 캔 정보에 대하여 물체 분할 과정을 잘 수행하는 것을 확인 할 수 있다.
Table 3은 데이터 세트에 대한 연산 시간 및 처리율을 나타낸다. 연산 시간은 한 스캔 라인에 대하여 평균 18~19ms가 소요되었다. 이에 대한 처리율은 52~55Hz 정 도이다. 사용한 레이저 측정 거리 센서의 프레임률(frame rate)은 37.5Hz이므로 센서의 프레임률과 비교해 볼 때 제안한 방법의 연산 속도가 1.5배 정도 빠른 속도를 보임 을 확인할 수 있다. 이는 제안한 방법이 실시간으로 동작 하며, 실제 주행하는 무인 자동차에도 적용할 수 있음을 나타낸다.
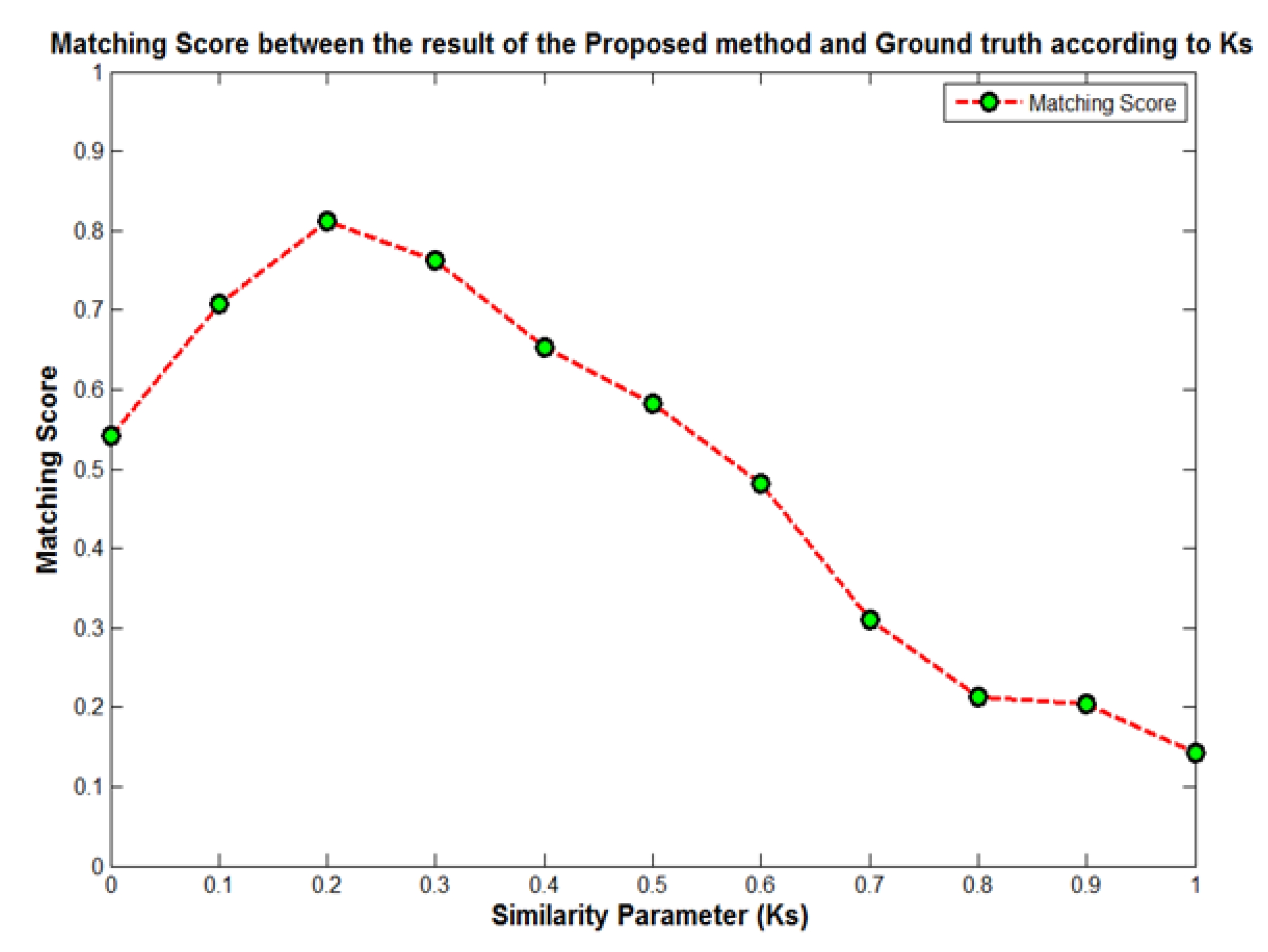
제안한 방법의 물체 수행 결과의 정확성을 판단하기 위 하여 KAIST/Málaga 데이터 세트의 Ground Truth를 제작 하여 이와 제안한 방법의 결과와 비교 ․ 분석하였다. Ground Truth와 제안한 방법과 물체 분할 정도가 어느 정 도 일치하는지 비교하기 위하여 Ground Truth와 제안한 방법 간의 매칭 점수(matching score)를 계산하여 이를 정 확성의 지표로 이용하였다. 본 논문에서는 매칭 점수를 계 산하기 위하여 [15]에서 소개된 점 단위의 물체 분할 비교 방식을 이용하였다. 매칭 점수는 Ground Truth와 제안한 방법과 물체 분할 정도의 일치율이 낮을수록 0에 가까워지 고, 일치율이 높을수록 1에 가까워진다. 제안한 방법은 2.4.2절에서 설명했듯이 수식 (6)의 ks에 따라 물체 분할 효과가 달라진다. Table 4와 Fig. 10은 ks에 따른 매칭 점 수의 변화를 나타낸다. 실험 결과, ks=0.2일 때 매칭 점수 가 가장 높음을 확인할 수 있다. 본 논문에서는 분석 결과 를 토대로 정확한 물체 분할 결과를 도출하기 위하여 최종 적으로 ks=0.2로 설정하고 실험하였다.
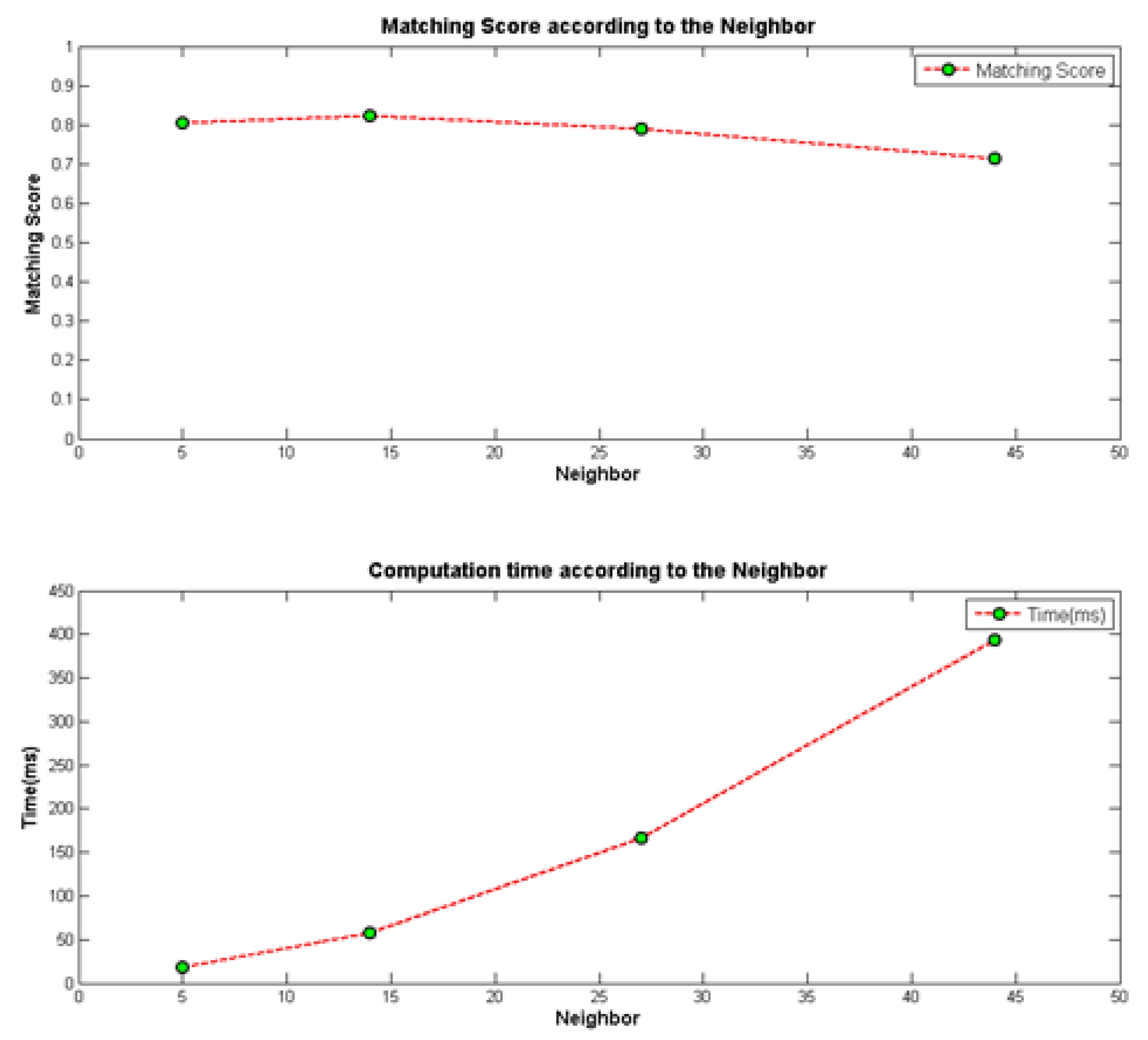
2.2절에서 언급했듯이 제안한 방법은 주변점 개수에 따 라 물체 분할의 정확성 및 연산 속도가 달라진다. Table 5 와 Fig. 11은 KAIST 데이터 세트에 대하여 주변점 개수의 변화에 따른 매칭 점수와 연산 속도의 변화를 나타낸다.
Table 5와 Fig. 11에서 확인할 수 있듯이 주변점의 개 수가 많아지면 매칭 점수가 높아져 정확성은 높아지나 주 변점의 개수가 과도하게 많으면 한 물체가 여러 개의 물체 로 분할되는 문제가 발생하여 오히려 매칭 점수가 떨어지 게 된다. 연산 시간의 측면에서는 주변점의 개수가 많아지 면 주변점을 조사하는데 많은 시간이 소요되므로 전체적인 연산 시간이 상승함을 확인할 수 있다. 본 논문에서는 5-NN이 매칭 점수가 0.805로 14-NN에 비하여 높지는 않 지만 18.33ms의 빠른 시간으로도 정확한 물체 분할 결과를 수행하므로 5-NN을 사용하였다.
Table 6은 앞선 실험 결과를 바탕으로 제안한 방법과 1절에서 소개한 기존의 연구와의 성능을 비교 및 분석한 것이다.
Table 6에서 확인할 수 있듯이 제안한 방법은 기존 연 구와는 달리 3차원 정보를 이용하여 실시간으로 비교적 정 확하게 물체를 인식함을 확인할 수 있다. Strom[5], Zhu[6]의 연구는 3차원 정보를 2차원 정보로 변환하여 처리한 것과 는 달리 제안한 방법은 3차원 정보를 그대로 이용하며, 그 럼에도 불구하고 물체의 인식에 대한 정확성은 같은 3차원 정보를 이용한 Golovinskiy[8]의 방법에 비해 좋은 성능을 보임을 확인할 수 있다. Zhu[6]의 연구에 비해 물체의 인식 에 대한 정확성은 높은 편은 아니지만 제안한 방법은 3차 원 정보를 실시간으로 처리하여 기존 연구에 버금가는 정 확성을 동시에 보장함을 확인할 수 있다.
4. 결 론
본 논문에서는 무인 자동차의 자율 주행을 위하여 레이 저 거리 측정 센서로 획득한 3차원 점군을 이용하여 도시 환경에서의 주변 환경 정보를 실시간으로 인식하는 방법을 제안하였다. 물체를 효과적으로 분할하기 위하여 그래프 모델을 이용하여 물체를 정확하게 분할하는 방법을 제안하 였으며, 제안한 방법을 입증하기 위하여 KAIST 캠퍼스 데 이터 세트를 구축하여 실험을 하였으며 추가적으로 공개된 Málaga 데이터 세트에 대해서도 실험을 함으로써 일반적 인 도시 환경에서도 적용 가능한 알고리즘임을 입증하였다. 그리고 발표된 연구와 물체의 인식률을 비교함으로써 알고 리즘의 우수성을 입증하였다. 또한 제안한 방법의 연산 속 도는 센서의 정보 처리 속도보다 1.5배 빠르므로 제안한 방 법이 실시간으로 동작 가능함을 확인할 수 있었다. 다시 말 하면 본 논문에서 제안한 방법은 센서 데이터의 획득에서 부터 물체를 분할하는 과정을 포함하는 의미 있는 지도 (semantic mapping)로 표현하는 종합적인 방법이라고 말 할 수 있다.
제안한 방법은 정확하고 의미 있는 3차원 정보를 제공 하기 때문에 추후에 정확하게 분할된 물체가 어떤 종류의 물체인지 인식하는 물체 분류에도 이용될 수 있을 것으로 보인다. 이는 무인 자동차의 자율 주행뿐만 아니라 차량 내 비게이션(navigation) 용도로 지도 정보를 효과적으로 이용 할 수 있으며, 더 나아가 정적/동적 물체를 탐지하거나 추 적하는 알고리즘에 적용하여 정확도를 높일 수 있을 것으 로 보인다. 또한, 색상 정보를 제공하는 카메라를 기존의 시스템에 융합하여 물체의 인식률 향상에 도움을 줄 수 있 는 다른 특징 정보를 제안하거나, 보다 정확한 차량과 물체 의 위치 정보를 획득하기 위해 DGPS, IMU와 같은 센서들 이 제공하는 정보를 효과적으로 융합하는 연구가 필요할 것으로 보인다.
References
-
Miller, I., , “Cornell University's 2005 DARPA grand challenge entry”, Journal of filed Robotics, (2006), 23(8), p625-652.
[https://doi.org/10.1002/rob.20136]

- Thrun, S., , “Stanley: The robot that won the DARPA Grand Challenge”, Journal of filed Robotics, (2006), 23(9), p661-692.
-
Dolgov, D., Thrun, S., Montemerlo, M., Diebel, J., “Path planning for autonomous vehicles in unknown semi-structured environments”, The International Journal of Robotics Research (IJRR), (2010), 29(5), p485-501.
[https://doi.org/10.1177/0278364909359210]

-
Baldwin, I., Newman, P., “Road vehicle localization with 2D push-broom LIDAR and 3D priors”, (2012, May), IEEE International Conference on Robotics and Automation (ICRA), p2611-2617.
[https://doi.org/10.1109/icra.2012.6224996]

-
Strom, J., Richardson, A., Olson, E., “Graph-based segmentation for colored 3d laser point clouds”, (2010, Oct), IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), p2131-2136.
[https://doi.org/10.1109/iros.2010.5650459]

-
Zhu, X., Zhao, H., Liu, Y., Zhao, Y., Zha, H., “Segmentation and classification of range image from an intelligent vehicle in urban environment”, Correction Review, (2010, Oct), IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), p1457-1462.
[https://doi.org/10.1109/iros.2010.5652703]

-
Zhao, X., He, M., Zhao, H., Davoine, F., Zha, H., “Computing object-based saliency in urban scenes using laser sensing”, (2012, May), IEEE International Conference on Robotics and Automation (ICRA), p4436-4443.
[https://doi.org/10.1109/icra.2012.6224940]

-
Golovinskiy, A., Kim, V.G., Funkhouser, T., “Shape-based recognition of 3d point clouds in urban environments”, Journal of Offender Counseling, Services and Rehabilitation, (2009, Sep), IEEE International Conference on Computer Vision (ICCV), p2154-2161.
[https://doi.org/10.1109/iccv.2009.5459471]

-
Wang, C.C., Thorpe, C., Thrun, S., Hebert, M., Durrant-Whyte, H., “Simultaneous localization, mapping and moving object tracking”, The International Journal of Robotics Research (IJRR), (2007), 26(9), p889-916.
[https://doi.org/10.1177/0278364907081229]

-
Newman, P., , “Navigating, recognizing and describing urban spaces with vision and lasers”, The International Journal of Robotics Research (IJRR), (2009), 28(11-12), p1406-1413.
[https://doi.org/10.1177/0278364909341483]

-
Klasing, K., Wollherr, D., Buss, M., “Realtime segmentation of range data using continuous nearest neighbors”, (2009, May), IEEE International Conference on Robotics and Automation (ICRA), p2431-2436.
[https://doi.org/10.1109/robot.2009.5152498]

-
Klasing, K., Althoff, D., Wollherr, D., Buss, M., “Comparison of surface normal estimation methods for range sensing applications”, (2009, May), IEEE International Conference on Robotics and Automation (ICRA), p3206-3211.
[https://doi.org/10.1109/robot.2009.5152493]

-
Felzenszwalb, P.F., Huttenlocher, D.P., “Efficient graph-based image segmentation”, International Journal of Computer Vision (IJCV), (2004), 59(2), p167-181.
[https://doi.org/10.1023/b:visi.0000022288.19776.77]

-
Blanco, J.L., Moreno, F.A., Gonzalez, J., “A collection of outdoor robotic datasets with centimeter-accuracy ground truth”, Autonomous Robots, (2009), 27(4), p327-351.
[https://doi.org/10.1007/s10514-009-9138-7]

-
Douillard, B., Underwood, J., Kuntz, N., Vlaskine, V., Quadros, A., Morton, P., Frenkel, A., “On the segmentation of 3D LIDAR point clouds”, (2011, May), IEEE International Conference on Robotics and Automation (ICRA), p2798-2805.
[https://doi.org/10.1109/icra.2011.5979818]