지구 물리정보를 이용한 무인잠수정의 복합 항법 기술
2Senior Researcher, Hanwha Systems, Daejeon, Korea seungwoo1.byun@hanwha.com
© Korea Robotics Society. All rights reserved.
Abstract
Alternative navigation in underwater environments is essential to prevent accumulating drift error of dead reckoning. In case of using an external positioning system, the installation and management process of the transmission station is cumbersome, and the operation range of underwater vehicle is limited. In order to solve this problem, navigation using geophysical information such as terrain, geomagnetic field and gravity can be used. Unlike the terrain, geomagnetic field and gravity are composed of 3-D information, so continuation process is required. In this paper, we present a integrated navigation algorithm using multiple geophysical information for long-term operation of UUV. The proposed algorithm is verified through numerical simulation in an artificially generated environments. As a result, integrated navigation showed higher navigation accuracy than single alternative navigation.
Keywords:
Underwater Navigation, Geophysical Navigation1. 서 론
최근 자동화/무인화 기술의 발전에 따라 다양한 분야에서 무인시스템의 적용이 활발히 이루어지고 있다[1]. 해양 분야에서 도 무인선박과 함께 무인잠수정(UUV, Unmanned Underwater Vehicle)의 유용성이 크게 주목받고 있다[2,3]. 무인잠수정은 장 시간 수중에 머물면서 다양한 해양환경 데이터를 수집하는 것 이 가능하며 군사적 목적으로 대기뢰전 및 대잠전에 등의 임 무에도 도움이 될 수 있다. 이와 같이 다양한 임무를 수행하기 위해서는 여러 기술이 요구되는데 그 가운데 가장 중요한 기 술이 이동체의 위치를 파악하는 항법(Navigation)기술이다.
항법(Navigation)은 무인이동체의 자율 운항을 위해서는 우 선적으로 해결되어야 하며 안정적인 항법 성능이 제공되어야 만 무인이동체들은 다양한 임무를 진행할 수 있다. 일반적인 무인이동체 항법의 경우 서로 보완적인 GPS와 관성 항법 시 스템(INS, Inertial Navigation System)을 복합적으로 사용한다. 관성 항법 시스템의 경우 짧은 시간 내에서 높은 정확도의 항 법 성능을 보유할 수 있으나 위치를 직접적으로 측정하는 것 이 아니라 가속도 혹은 속도 성분을 적분하여서 위치를 예측 하기 때문에 시간이 지날수록 오차가 필연적으로 누적되는 문 제가 있다. GPS의 경우 알고 있는 위성의 위치에서 발송된 통 신 정보를 이용하여 위치를 직접 측정하므로 위치 오차가 상 대적으로 크게 발생하지만 누적되지는 않는다. 이에 따라, GPS/INS 복합 항법 시스템을 이용하면 위치의 누적 오차 없이 상시 정확한 위치 추정이 가능하다.
수중 환경에서는 전자기파의 불투과성으로 인해 GPS의 사 용이 불가능해지기 때문에 관성 항법 시스템의 누적 위치 오 차 문제를 해결해줄 수 있는 다른 방법이 필요하다. 먼저, GPS 와 비슷한 원리를 이용하여 알려진 위치에서 음파 신호를 전송 해 줄 수 있는 위부 측위 시스템을 사용할 수 있다[4,5]. 대표적인 측위 시스템으로 LBL (Long Baseline), SBL (Short Baseline), USBL (Ultra Short Baseline) 등이 있으며 이들은 사용하는 신 호 처리 방법이 각기 다르나 각 시스템의 이름이 암시하듯 송 신소간의 거리에 따라 구분된다. 송신소간 거리가 USBL의 경 우 10 cm 이내, SBL의 경우 20~50 m, LBL의 경우 100~2000m 정도에서 이용된다. LBL은 무인잠수정의 운용깊이에 상관없 이 높은 항법 정보를 제공가능하다는 이점이 있으나 송신소의 설치 및 회수과정이 번거롭다. 외부 측위 시스템을 사용하더 라도 무인잠수정의 운용 범위가 수 km 이내에서만 사용이 가 능하므로 장기간 먼 거리를 운용해야 하는 무인잠수정의 경우 에는 적용되기 어렵다는 문제가 발생한다.
관성 항법 시스템의 누적 오차를 줄이기 위한 다른 방법으 로서는 지구물리적인 정보를 이용하여 절대 위치를 측정하는 방법이 있다. 이용 가능한 정보는 지형, 지구지자기, 지구중력 장이 있으며[6,7] 지형 정보를 이용해서 위치를 하는 지형 참조 항법(Terrain Referenced Navigation)의 경우 GPS 등장 이전부 터 항공 시스템의 항법에 적용되어 활발히 연구가 진행된 바 있다. 지형 참조 항법의 경우 지형을 측정하기 위해서 음파를 방출하고 해저 지면에 반사되어서 돌아오는 파동을 수신하기 때문에 사용되는 에너지가 많고 군사적 목적으로 활용 시 적 에게 발각되기 쉽다는 단점이 있다. 반면, 지구지자기 및 지구 중력장을 이용하여 항법을 진행하는 경우 수동적인 센서를 사 용하기 때문에 에너지 소모가 적고 탐지 가능성이 낮아진다. 하지만, 거리에 따른 중력장 및 자기장의 변화가 극미하기 때 문에 사용하는 센서의 정확도가 매우 높아야한다는 점, 해저 지형과 달리 삼차원 정보를 필요로 하기 때문에 항법 정보로 서 사용하는데 더욱 많은 정보 처리 과정이 요구된다는 점의 문제점을 지닌다. 이에 따라서, 아직 실험을 통해서 지구물리 항법을 검증한 연구는 많이 이루어지지 않았다.
본 논문에서는 지형, 지구지자기 및 중력장 정보를 모두 사 용하여 장기간, 장거리 잠항을 하는 경우에도 안정적인 항법 을 진행할 수 있는 복합 항법 알고리즘을 제시한다. 제시하는 복합 항법 알고리즘은 가상으로 생성된 지형 및 지자기 지도 에서 시뮬레이션을 통해 검증하였다
2. 수중 항법
2.1 관성 항법
관성 항법 시스템은 회전운동을 측정하는 자이로와 가속도 를 측정하는 관성 센서(IMU, Inertial Measurement Unit)를 사 용하여 이동체의 각속도 및 가속도를 측정하고 이전의 이동체 의 위치 및 자세를 기반으로 이동한 거리를 예측하여 항법 정 보를 제공한다. 이 과정에서 측정된 가속도와 각속도를 적분 하게 되며 센서의 측정 오차도 같이 누적되기 때문에 시간이 지나면 점점 큰 오차를 보유하게 된다. 수중시스템의 경우 초 음파속도계(DVL, Doppler Velocity Log)를 사용하면 속도를 측정할 수 있기 때문에 누적되는 오차를 크게 줄일 수 있다.
관성 항법 시스템을 더욱 정밀하게 구축하기 위해서는 추 정 필터 설계를 고도화할 수 있다. [8]의 경우 간접 되먹임 필터 (Indirect Feedback Kalman Filter)를 이용하여 관성센서 및 초 음파 속도센서 기반의 수중 복합항법 알고리즘을 제안하였으 며 [9]은 안정적인 속도 추정필터를 구성하기 위해 수력학 모 델을 사용하여 장시간 수중항법성능을 개선하였다.
하지만, 관성 항법 시스템만을 이용하는 경우 누적되는 오 차를 막을 수는 없다는 본질적인 한계가 있기 때문에 절대 위 치를 측정하여 오차를 보상해주는 방법이 요구된다.
2.2 지형 참조 항법
지형 참조 항법은 무인잠수정의 위치 파악을 위해 운용 중 인 수역의 해저지형 정보를 이용하는 기술이다. 해수면으로부 터 해저면까지의 깊이 분포를 나타내는 해저 지형 지도가 주 어져있을 때, 이동체의 위치에서 해저 지면까지의 거리를 측 정하고 측정값과 해저지형을 대조하여 이동체의 수평면 위치 를 추정할 수 있다. 이동체의 수면으로부터 깊이는 압력계로 쉽게 측정이 가능하며 수면으로부터 깊이와 해저면까지의 거 리의 합이 해저 지형지도와 일치한 곳에 이동체가 위치할 것 으로 추정한다. 단, 조수 간만의 차 등에 의한 조위 변화도 고 려해 주어야 하지만 일반적인 조위 변동은 주기적으로 일정한 변화를 보유하고 있기 때문에 이를 알 수 있다고 가정한다.
지형참조항법의 범주는 크게 지형의 윤곽을 대조하는 TERCOM (Terrain Contour Matching)과 측정된 지형 고도를 독립적으 로 이용하여 위치를 보정하는 SITAN (Sandia Inertial Terrain Aided Navigation) 두 가지로 구분된다. SITAN의 방식이 상대적으로 계 산소모량이 적어서 사용하기 유리하나 관성항법의 오차가 잔 재한 상황에서 지형의 기울기를 예측하는 과정이 요구되어 비선 형 상태 추정 문제를 정확하게 해결하는 기법이 요구된다. 최근에 는 연산처리능력의 급격한 향상에 힘입어 칼만 기반 필터보다는 입자필터(PF, Particle Filter) 또는 점질량필터 (PMF, Point Mass Filter)를 적용하여 이를 해결하려는 시도가 늘어나고 있다[10,11].
입자 필터는 다음과 같은 과정으로 진행된다. 1) 각 입자는 가능한 상태 추정값을 가지며 계측값과 얼마나 부합되는지의 확률을 지니는 하나의 후보군이 된다. 2) 입자들은 시간이 지 남에 따라 상태 방정식에 따라 변화한다. 3) 각 입자가 보유한 확률값에 기반하여 상태 추정 분포 함수가 나타내진다. 입자 필터에서 이용되는 입자의 수가 증가할수록 입자들이 대표하 는 상태변수는 실제 상태 확률 분포 함수에 더욱 근접하게 나 타내지며 비선형 상태 추정 문제의 최적해에 수렴한다.
| (1) |
| (2) |
여기서 는 (i) 번째 입자가 가지고 있는 중요도(Importance weight)를 의미한다.
중요도는 연속적 중요도 추출(SIS, Sequential Importance Sampling) 과정을 통해 누적된다. 현재 상태값을 추정하기 위 해서 다음과 같은 가정을 이용하여 재귀적으로 중요도를 계산 할 수 있다.
| (3) |
| (4) |
연속적 중요도 추출방법의 경우 시간의 지남에 따라 중요 도 값이 점점 편향됨에 따라 적은 숫자의 입자만 의미 있는 중 요도 값을 보유하게 된다. 이에 따라, 중요도 값이 0에 가까워 진 입자의 경우 제거하고 같은 수만큼 높은 중요도 값을 가진 입자를 복제하는 방식의 재표본화(Resampling) 과정을 통해 입자 필터 성능을 유지할 수 있다.
입자 필터를 이용하는 경우 높은 비선형시스템에서도 강건 하게 상태 추정이 가능해진다는 장점을 보유하고 있으나 상태 수의 증가에 따라 입자 필터에 사용되는 입자의 수가 기하급 수적으로 증가해야하므로 매우 높은 계산량이 요구되는 문제 가 발생한다. [12]의 경우 이러한 문제를 해결하기 위하여 높은 비선형성 혹은 비정규분포 특성이 강한 변수는 입자 필터로 이러한 특성이 상대적으로 약한 변수는 정규 분포 기반의 해 석적 추정 기법으로 추정하는 라오-블랙웰라이즈드 입자 필 터(Rao-BalckWellized PF)를 사용하였다. 이에 따라, 지형의 기울기와 관련되어 있는 상태 변수인 위치 (x, y)는 입자 필터 를 이용해서 추정하고 다른 상태 변수(자세, 속도, 각속도, 가 속도)는 확장 칼만 필터를 사용하여서 추정하였으며 이 경우, 확장 칼만 필터로 모든 상태 변수를 추정할 때 보다 항법 필터 가 발산하지 않고 높은 항법 성능을 제공함을 보였다.
2.3 지자기 대조 항법
지구 자기장은 해저면 하부에 있는 물체의 물성과 분포에 따라 달라질 수 있으며 공간 상 위치에 따라 고유의 특성을 갖 는 값이므로 항법에 이용될 수 있다. 운용중인 무인잠수정이 계측한 지구자기장 값과 기존에 작성된 지자기 지도를 비교함 으로써 상대적인 이동체의 위치를 구한다. 상태 추정 문제의 관점에서 보았을 때 비교하는 대상의 변경이 있으나 지형 참 조 항법과 비슷한 방식으로 항법 필터를 구현할 수 있다. 다만, 지자기 정보의 특성 및 계측 방식에 따른 차이가 발생한다.
지구자기장은 쌍극성의 형태로 간주되며 지구 핵의 대류현 상으로 인해 자기장의 크기와 방향이 천천히 변화하는 것으로 알려져 있다. 지구자기장의 크기는 극지방에서 60μT, 적도 근방에서 30μT 값을 가진다. 또한, 태양 복사에 따라서 하루 주기로도 값이 변화하며 일반적으로는 수 nT 범위에서 값이 변화하지만 지구 자기 적도 부근에서는 100 nT 값의 변화도 발생가능하다. 더불어서, 자기 폭풍 등의 영향에 의하여 수 시 간에서 최대는 수 일 까지 자기장의 변화가 발생할 수 있다. 이 러한 변칙에 의하여 지구 전체적으로 자기장의 크기가 변화하 는 경우 고정된 위치에서 변하는 자기장의 크기를 측정하여 보상해주는 방법이 가능하다.
지구 자기장은 자기력계(Magnetometer)를 이용하여 측정 하며 측정하는 방식에 따라 두 가지의 종류로 나눠진다. 세슘 자기력계와 같은 스칼라 자기력계는 측정위치에서의 자기장 의 크기만을 측정하며, 플럭스 게이트 자기력계는 자기 벡터 성분의 크기를 직접 측정한다. 또한, 2개 이상의 자기력계를 이용하여 자력의 변화율을 측정하는 자력구배측정기(Magnetic gradiometer)를 이용할 수도 있다. 자력구배측정기를 이용한 경우 시간에 따라 변화하는 자기장의 영향을 고려하지 않아도 되는 장점을 가진다.
지자기는 지형과 달리 3차원 공간상에서 정의되는 물리량 이므로 항법에 활용하기 위해서는 3차원 지자기 지도를 필요로 한다[13]. 하지만 수중 지자기 지도를 작성하는 과정은 굉장히 번 거로우며 수중 깊이 별 지자기 지도를 보유하고 있는 것은 사실 상 불가능하다. 이에 따라, 2차원 평면상에서의 지자기 정보를 알고 있을 때 이를 깊이에 따라 변하는 정도를 추정하는 연속화 (Continuation) 기법들이 연구된 바 있다. [Fig. 1]은 깊이에 따라 자기장의 크기가 변화하는 예시를 보인다. 연속화 기법을 위해 서는 지자기장을 변화시키는 원천이 멀리 있다는 가정이 필요 한데, 무인잠수정이 운용되는 수중 환경에서 지자기를 변화시 키는 변체(Anomaly)의 경우 해저 지반의 광물로 간주되므로 잠 항하는 무인잠수정이 해저면 바로 근처에서 운용되지 않는 경 우라면 합당한 가정으로 여겨진다. 이에 따라, 수상선으로 해수 면에서 2차원 지자기장 지도를 작성하고 연속화 기법으로 수중 지자기 분포를 추정하여 무인잠수정의 항법이 진행될 수 있다.
지자기 연속화 기법은 지자기장의 세기가 지자기 원천과의 거리에 따라 달라지는 특성을 수학적으로 모델링 하여 이루어 진다. 지자기 원천으로부터 멀어지는 위 방향으로의 연속화는 지가지장의 세기를 완화하고 아래 방향으로의 연속화는 지자 기장의 세기를 강화하여 이루어진다. 지자기장의 세기 변화가 비선형성을 지니면서 변화하기 때문에 다음과 같은 변환과정 을 통한 해석적인 기법을 이용한다.
M이 관측되는 스칼라 자기장의 변체이며 지구 자기장에 비해 작은 값을 가진다면 라플라스 방정식을 만족한다.
| (5) |
지자기 원천과 멀어지는 방향으로의 연속화는 진동수 영역 으로 변환하여 계산할 수 있다. 한 축의 지자기 정보를 푸리에 변환을 이용하면 다음과 같이 표기 된다.
| (6) |
여기서 ∆z는 수직 거리를, w는 진동수를 나타낸다.
이를 이차원 평면의 지자기 정보 형태로 확장하기 위해서는 힐베르트 변환을 도입한다. 퍼텐셜 장의 수직 방향에서의 자기 장 변화는 다음과 같은 힐베르트 변환과정을 통해 계산된다.
| (7) |
이에 따라, 삼차원의 지자기 연속화 과정은 다음과 같이 계 산된다.
| (8) |
| (9) |
*는 콘볼루션, 를 나타낸다.
위의 연속화 기법은 해석적인 기법을 기반으로 하나 실제 데이터에서 적용하기는 불안정한 측면이 있다. 특히, 지자기 원천과 가까워지는 아래 방향의 연속화에서는 높은 진동수를 지닌 노이즈의 값이 증폭되는 문제가 발생하고 또한, 평면 지자 기 데이터가 유한적이기 때문에 발생하는 Edge effect 문제가 생 겨서 정확한 자기장 값을 유추하기 어렵다. 수중 환경에서는 수 상선으로 취득한 자기장의 정보를 아래 방향으로 연속화 해야 하므로 이러한 문제를 해결하기 위해서 안정적인 아래 방향의 연속화 기법(Stable Downward Continuation)을 도입해야 한다.
[14]는 고주파 노이즈를 줄이기 위한 저주파 통과 필터를 이 용한 Tikhonov 정규화 과정을 이용하여 안정적인 아래 방향의 연속화 기법을 적용할 때 사용되는 정규화 변수 α를 결정하는 방법을 제시한다. 정규화 변수 α는 기존 연속화 기법의 결과 와 저주파 통과 필터 사이의 균형을 맞추는 역할을 하며 이상 적인 α 값은 연속화 과정이 이루어지는 지도에 따라 달라진 다. 두 인접한 α값에서 구한 연속화 결과 차이의 C-norm 값 을 α값에 따른 함수로 나타내었을 때 국부 최소치를 가지는 α 값이 이상적인 값으로 알려져 있으나 데이터 표본 수가 적은 경우에는 Lp-norm을 사용할 때 더 좋은 결과를 제공하기도 한다. 기존 연속화 기법을 사용시에는 데이터를 취득한 간격 의 길이의 2배에서 10배 정도의 깊이 까지만 연속화가 가능하 였으나 Tikhonov 정규화 과정을 이용하면 고주파 노이즈가 많 이 제거된 안정적인 결과를 보여준다. 단, 단위 격자 데이터의 한계로 인해, 지자기 원천의 영향이 약해서 상층의 지도에서 주파수 단위로 분리하기 어려운 신호는 연속화를 통하여 복구 할 수 없어, 해양 표면의 데이터를 매우 깊은 수심에서의 사용 하기는 어렵다.
2.4 중력장 대조 항법
지구 중력장은 지구 내외의 모든 물체로부터 발생하는 만 유인력장의 합으로 위치에 따라 주변 지형 및 밀도에 의해 변 화한다. 자기장 대조 항법과 마찬가지로 운용중인 무인잠수정 이 계측한 중력값과 기존에 작성된 중력 지도를 비교함으로써 상대적인 이동체의 위치를 구한다. 절대 중력을 측정할 경우 운동체가 중력을 측정 과정에서 섞이는 운동체의 가속도정보 를 분리하기 어렵다는 문제가 있어 중력값을 직접 측정하기보 다는 중력장의 2차 미분 텐서를 구하는 중력구배계(Gravity Gradiometer)를 이용하는 것이 일반적이다.
지구 중력에 영향을 주는 지형 및 밀도는 시간에 따라 변하 는 정도가 매우 느리므로 자기장에 비해 데이터 변화가 적고 안정적이다. 태양 및 달의 움직임에 따라 중력이 변화하나 이 또한 시간과 태양 및 달의 대략적인 위치를 알면 보정할 수 있 다. 그러나 거리에 따른 중력의 변화하는 정도는 매우 작으므로 항법에 사용하기 위해서는 매우 높은 성능의 센서가 요구된다. 국립해양조사원의 선상 중력 자료[15]에 따르면 한반도 주변 해 역의 중력 이상은 –40 mgal 에서 60 mgal 까지 변화함을 보인다.
수중에서 중력장을 계산할 때, 해수와 같은 질량을 가진 연 속체 내의 중력장은 다음의 푸아송 방정식을 만족한다.
| (10) |
여기서 G는 중력상수, ρ는 해수의 밀도를 나타낸다.
측정 위치와 원하는 위치 사이에 해수 이외의 물체가 없다 는 가정하에 중력장을 자기장과 같이 연속화할 수 있도록 중 력장을 다음과 같이 특수해와 일반해로 분리할 수 있다.
| (11) |
| (12) |
라플라스 방정식을 만족하는 일반해의 단일 방향 변화량은 마찬가지로 라플라스 방정식을 만족한다. 따라서 중력에 대해 다음과 같이 연속화 기법을 사용할 수 있다.
| (13) |
| (14) |
항법에서는 연속화된 지도의 중력 변화량만을 사용하므로 특수해의 값은 무시할 수 있다.
2.5 복합 항법
지형참조항법은 지형의 변화가 풍부한 수역에서는 충분한 항법 정밀도를 제공할 수 있으나 평평한 해저 지형이 계속될 경우 그 성능이 급격히 저하된다. 반면에 지자기 대조 항법은 지형의 굴곡보다는 지반을 구성하는 물질에 따라 지자기 분포 가 변화하므로 그 특성이 지형의 굴곡과는 연관성이 없다. 중 력장의 경우 지형의 높이와 지반을 구성하는 물질이 모두 영 향을 미치지만 이 또한 지자기장 변체를 생성하는 물질과는 다르므로 사용되는 특성이 다르다. 이러한 세 가지의 지구물 리적 특성이 상호 보완적으로 이용되면 항법 성능을 더욱 높 일 수 있을 것으로 기대할 수 있다.
복합 항법 추정 필터를 구성하기 위하여 비동기 측정 갱신 방식을 사용한다. 각 지구 물리적 정보를 측정하는 센서의 측 정 주기가 동일하지 않고 서로 동기화되지 않으므로 측정 센 서 사이에 상관관계가 없다고 가정하여 순차적으로 측정 갱신 과정을 진행한다. 각 측정값이 들어오면 실시간으로 비동기 적 측정 갱신 과정이 이루어진다.
이러한 비동기 측정 갱신 방법에는 무인잠수정의 운용 시 나리오에 따라 쉽게 응용가능하다는 장점을 지닌다. 생태적인 목적 혹은 군사적 목적으로 인해 소나를 사용하지 못하는 상 황에서는 선택적으로 지자기 및 중력장 정보만을 이용하여서 항법에 활용할 수 있다.
3. 수치적 검증
3.1 가상 환경 생성
시뮬레이션을 위한 지형은 프랙탈 브라운 운동을 기반으로 한 무작위 지형 형성 알고리즘을 통하여 제작하였다([Fig. 2]). 제작된 지형은 수평 방향으로 2 km 의 너비를 지니며 지형 높 이의 최대 차이가 20 m 정도 된다. 지형의 높낮이 변화 정도는 해역에 따라서 크게 다르나 서해 태안 연안 지형의 경우 1 km 구간에서 최대 차이가 40 m 가량 발생하기도 하였으므로[16] 합당한 가상 환경으로 간주된다. 격자 간격은 5 m로 그 사이에 위치해 있는 높이는 선형 보간법을 이용하여 계산한다. 제작 된 가상의 지형 지도는 아래와 같다.
중력 이상 지도의 경우 중력의 변화가 지형의 높이에 의해 서만 발생한다고 가정한다. 중력 변화 정도는 한반도 주변해 역에서 조사된 중력장 크기 변화[17]와 비슷하게 설정될 수 있 도록 해저 지각 밀도를 설정하여 구성하였다.
중력 이상 정보를 구하기 위해 각 픽셀을 기준으로 그 픽셀 에 있는 질량이 각 높이에 가하는 수직 방향 중력을 계산하여 합하였다. 계산의 효율성을 위해 같은 픽셀에 있는 질량은 모 두 같은 수평 위치에 있다고 가정하였다. 한 픽셀의 질량이 한 위치에 가하는 수직 방향 중력은 다음과 같다.
| (15) |
dmin과 dmax는 각각 측정 위치와 해당 픽셀 질량 사이의 최 소 및 최대 거리이다. [Fig. 3]은 지형지도를 기반으로 계산된 수면에서의 2차원 중력장 분포를 보여준다
자기장 지도의 경우, 지형 아래에 서로 다른 쌍극모멘트 밀 도와 크기를 가진 직사각형 모양의 자성 물체가 존재한다고 가정하여 제작한다. 자기장 이상 값은 지구 자기장에 비해 매우 작은 값이라는 가정하에 한 위치의 쌍극모멘트가 다른 위치에 가하는 스칼라 자기장 모멘트는 다음과 같다.
| (16) |
자기장 분포의 경우에도 실제로 측정된 자기장의 변화 분 포와[18,19] 비슷한 형태로 구성하기 위하여 쌍극모멘트의 밀도 를 정하여 현실성 있는 자기장 지도를 제작하였다([Fig. 4]).
3.2 상태 변수 모델
본 연구에서는 지구 물리정보를 이용한 수중 항법에 관하 여 논의하고 있으므로 이동체의 동역학 모델은 고려하지 않고 시뮬레이션을 구성하였다. 무인잠수정의 자세에 따라서 측정 되는 지형 깊이와 중력이 달라질 수 있으나 장거리를 잠항하 는 무인잠수정의 운용 특성상 자세 제어는 정밀하게 이루어질 것이다. 이에 따라, 무인잠수정은 수평방향으로만 기동하며 6 m/s의 일정한 속력을 유지하는 것으로 간주하였다. 추정하는 이동체의 상태 변수는 다음과 같이 수평방향의 위치, 수면으 로부터 깊이, 수평방향의 속도로 구성된다.
| (17) |
3.3 계측 모델
이동체의 기본적인 항법 성능을 제공하기 위하여 관성항법 센서들을 사용한다. 이동체의 수면으로부터 깊이는 압력계를 이용하여 측정될 수 있고, 수평방향의 속도는 자이로 및 가속 도 센서를 이용하여 추정하거나 초음파속도계를 통해 바로 측 정가능하다. 시뮬레이션에서는 지구물리항법의 성능을 강조 하기 위하여 관성항법의 성능을 의도적으로 낮게 설정하였다.
지형 참조 항법에서 사용되는 수중 깊이 측정 센서의 경우 측면 주사 음향기(Side Scan Sonar) 혹은 다중빔 음향측심기 (Multibeam Echsounder)를 이용하면 1회 계측 시 많은 양의 지 형정보를 측정가능 하지만 본 시뮬레이션에서는 지형의 윤곽 을 이용하는 것이 아니라 측정 깊이를 직접 이용하는 SITAN 기법을 이용하므로 단일빔 초음파 고도계(Single-beam Acoustic Altimeter)를 사용한다고 가정하였다.
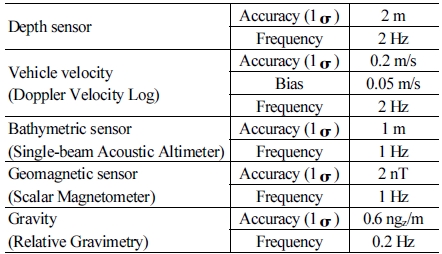
지자기 대조 항법에서는 자기장의 크기를 측정하는 스칼라 자기력계를 사용하였으며 중력 장 대조 항법에서는 상대 중력 측정 장치(Relative gravimetry)를 이용하여 각 수평 방향으로의 중력 변화도를 측정할 수 있는 것으로 하였다. 각 센서 정확도의 경우 알려진 가장 최신의 센서 해상도를 기준으로 설정되었다.
수중 깊이 측정 센서의 경우 이동체와 해저 지형과의 거리 에 따라서 센서 해상도가 달라지는 것이 일반적이지만 본 논 문에서는 동일한 해상도를 가지고 있는 것으로 가정하였다. 자기력계 및 상대 중력 측정 장치는 수중 깊이에 상관없는 센 서 해상도를 가지지만 이동체는 수상에서 측정된 중력장 및 자기장 지도만을 가지고 있다고 가정하므로 수중에서 중력장 및 자기장을 측정하는 경우에는 연속화 과정을 통하여 추측한 정보를 기반으로 대조 항법을 진행하여 측정 모델에 오차를 내재 한다. 본 시뮬레이션에서 사용된 센서의 파라메터는 [Table 1]에 나타내었다.
3.4 시뮬레이션
확장 칼만 필터를 이용하여 이동체의 관성 항법을 구성하 고 입자 필터를 이용하여서 지구물리항법으로 이동체의 위치 를 추정하는 항법 시스템을 구축하였다. 이동체가 2 km 범위 의 지역 안에서 [Fig. 5]와 같은 잔디깎기 패턴 형태로 움직일 때 발생하는 항법 오차를 통해서 각 항법 성능을 평가한다. 지자기 장 및 중력장의 삼차원 연속화 과정의 성능을 파악하기 위하여 무인잠수정의 깊이 별 성능 테스트를 진행하였으며 모든 경우 에 대해서 20번씩 Monte-Carlo 시뮬레이션을 진행하였다.
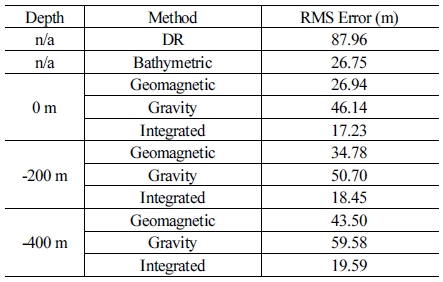
각 시뮬레이션에서 추정한 이동체 경로의 평균 제곱근 오 차를 평균하여 [Table 2]에 나타내었다. 관성 추측 항법(Dead Reckoning, DR)의 경우 DVL을 통해 이동체의 속도값을 알 수 있다고 가정하였으며 각 지구 물리정보를 이용한 지형참조항 법, 자기장 대조 항법, 중력 대조 항법은 각 방법에 해당하는 지구 물리정보를 추가적으로 측정할 수 있다고 가정하였다. 복합 항법의 경우 이동체의 관성 정보 및 모든 지구 물리정보 를 얻을 수 있을 때 항법 성능을 나타낸다.
지형 참조 항법은 지자기 대조 항법 및 중력장 대조 항법에 비하여 높은 항법 정확성을 제공해주지만 지형 깊이 정보를 측정하기 위하여 능동 소나를 이용해야하므로 운용 시나리오 에 따라 사용 한계가 발생할 수 있다. 지자기 대조 항법 및 중력 장 대조 항법의 경우에도 추측 항법에 비해서는 월등히 높은 항법 성능을 보유하며 누적되는 표류 오차를 막아줄 수 있다 는 점에서 무인잠수정의 운용 시간이 길수록 항법 정확도의 효과는 더욱 두드러질 것이다.
지자기 및 중력장을 이용하는 경우 삼차원 연속화 과정에 서 발생하는 오차에 의하여 무인잠수정 운용 깊이가 깊어질수 록 항법 성능이 저하된다. 변체에서 생성되는 지자기장 및 중 력장의 경우 각 거리의 제곱 및 세제곱으로 줄어드는 효과를 가지므로 연속화 과정에서 발생하는 오차는 무인잠수정의 운 용 깊이가 깊어질수록 더욱 크게 발생한다. 그럼에도 시뮬레 이션 결과에서 볼 수 있듯이 1200 m 수심의 환경에서 400 m 깊 이에서의 운용에서도 추측 항법 보다 더 높은 항법 성능을 보유 할 수 있었다. 실제 무인잠수정의 운용에서는 이보다 더 깊게 운용할 경우는 드물 것이므로 항법 적용의 유효성을 지닌다.
지형 참조 항법, 지자기 대조 항법 및 중력장 대조 항법을 모 두 결합한 복합항법의 경우 항상 가장 높은 항법 결과를 제공 하였다. 단일 센서를 활용한 항법 중 가장 높은 정확도를 지닌 지형 참조 항법 대비 해수면에서 36%의 정확도 향상을 보였으 며 수심 400 m 깊이에서도 약 27%의 성능개선이 일어났다. 소 요된 계산 시간은 각 센서 측정 주기에 달라지기는 하나, 지형 참조 항법 대비 30% 정도 증가하였다.
4. 결 론
관성 항법의 표류 오차를 줄이기 위해서는 이동체의 위치 를 직접 추정할 수 있는 대체 항법 기술이 요구된다. 수중 환경 에서 이용될 수 있는 대표적인 대체 항법으로는 지형 참조 항 법, 지자기 대조 항법, 중력장 대조 항법이 있다. 본 논문에서 는 제시된 각 대체 항법을 적용할 수 있는 시스템을 구성하고 이들을 통합하는 복합 항법 알고리즘을 구성하였다. 수치적 시뮬레이션을 통해서 복합 항법의 성능을 검증하였으며, 제시 한 복합항법의 성능은 기존 단일 센서의 대체 항법 대비 약 30%의 정확도 향상을 보였다.
Acknowledgments
This work was supported by a grant-in-aid of HANWHA SYSTEMS.
References
-
H. Jo, H. M. Cho, S. Lee, and E. Kim, “A Deep Convolutional Neural Network Based 6-DOF Relocalization with Sensor Fusion System,” The Journal of Korea Robotics Society, vol. 14, no. 2, pp. 87-93, Jun., 2019.
[https://doi.org/10.7746/jkros.2019.14.2.087]

-
D. Hwang, M. Jang, and J. Kim, “Development of a Low-cost Unmanned Underwater Vehicle and Performance Verification,” The Journal of Korea Robotics Society, vol. 13, no. 2, pp. 103-112, Jun., 2018.
[https://doi.org/10.7746/jkros.2018.13.2.103]

-
J. Han, Y. Cho, and J. Kim, “Coastal SLAM with Marine Radar for USV Operation in GPS-Restricted Situations,” IEEE Journal of Oceanic Engineering, vol. 44, no. 2, pp. 300-309, Apr., 2019.
[https://doi.org/10.1109/JOE.2018.2883887]

- P.-M. Lee, B.-H. Jeon, S.-M. Kim, C.-M. Lee, U.-K. Lim, and S.-I Yang, “A Hybrid Navigation System for Underwater Unmanned Vehicles, Using a Range Sonar,” Journal of Ocean Engineering and Technology, vol. 18, no. 4, pp. 33-39, 2004.
- K. Kim, H.-T. Choi, S.-M. Kim, P.-M. Lee, C.-M. Lee, and S.-K. Cho, “Implementation of Deep-sea UUV Precise Underwater Navigation based on Multiple Sensor Fusion,” Journal of Ocean Engineering and Technology, vol. 24, no. 3, pp. 46-51, 2010.
-
J. Melo and A. Matos, “Survey on advances on terrain based navigation for autonomous underwater vehicles,” Ocean Engineering, vol. 139, pp. 250-264, 2017.
[https://doi.org/10.1016/j.oceaneng.2017.04.047]

- H. Rice, S. Kelmenson, and L. Mendelsohn, “Geophysical navigation technologies and applications,” PLANS 2004. Position Location and Navigation Symposium (IEEE Cat. No.04CH37556), Monterey, CA, USA, pp. 618-624, 2004.
- C.-M. Lee, P.-M. Lee, and W.-J. Seong, “Underwater Hybrid Navigation Algorithm Based on an Inertial Sensor and a Doppler Velocity Log Using an Indirect Feedback Kalman Filter,” Journal of Ocean Engineering and Technology, vol. 17, no. 6, pp. 83-90, 2003.
-
Y. Lee, W.-S. Ra, K. Kim, M. Ahn, and B.-J. Lee, “Gertler- Hagen Hydrodynamic Model Based Velocity Estimation Filter for Long-term Underwater Navigation Without External Position Fix,” The Transactions of the Korean Institute of Electrical Engineers, vol. 65, no. 11, pp. 1868-1878, 2016.
[https://doi.org/10.5370/KIEE.2016.65.11.1868]

-
T. Kim, J. Kim, and S.-W. Byun, “A comparison of Nonlinear Filter Algorithms for Terrain-Referenced Underwater Navigation,” International Journal of Control, Automation and Systems, vol. 16, no. 6, pp. 2977-2989, 2018.
[https://doi.org/10.1007/s12555-017-0504-5]

-
J. Kim and T. Kim, “Terrain-Based Localization Using Particle Filter for Underwater Navigation,” International Journal of Ocean System Engineering, vol. 1, no. 2, pp. 89-94, 2011.
[https://doi.org/10.5574/IJOSE.2011.1.2.089]

-
T. Kim, J. Kim, and H.-T. Choi, “Terrain-referenced Underwater Navigation using Rao-Blackwellized Particle Filter,” Institute of Control, Robotics and Systems, vol. 19, no. 8, pp. 682-687, 2013.
[https://doi.org/10.5302/J.ICROS.2013.13.9014]

-
Francisco C Teixeira and Antonio M Pascoal, “Geophysical navigation of autonomous underwater vehicles using geomagnetic information,” IFAC Proceedings Volumes, vol. 41, no. 1, pp. 178-183, 2008.
[https://doi.org/10.3182/20080408-3-IE-4914.00032]

-
R. Pavteka, R. Karcol, D. Kusnirak, and A Mojzes, “Regcont: A matlab based program for stable downward continuation of geophysical potential fields using Tikhonov regularization,” Computers & Geosciences, vol. 49, pp. 278-289, Dec., 2012.
[https://doi.org/10.1016/j.cageo.2012.06.010]

-
A. Y. Jung, K.-S. Choi, Y-.C. Lee, and J. M. Lee, “External Gravity Field in the Korean Peninsula Area,” The Korean Society of Economic and Environmental Geology, vol. 48, no. 6, pp. 451-465, 2015.
[https://doi.org/10.9719/EEG.2015.48.6.451]

-
T. Kim, J. Kim, and S.-W. Byun, “A comparison of nonlinear filter algorithms for terrain-referenced underwater navigation,” International Journal of Control, Automation and Systems, vol. 16, no. 6, pp. 2977-2989, 2018.
[https://doi.org/10.1007/s12555-017-0504-5]

- C. Lee, et al., “Marine Geological and Geophysical Study for compiling Marine Geological Maps around the Dok Island in the East Sea, Korea,” Korea Institute of Geology, Minning, Materials, Daejeon, Korea, GOVP1199804862, pp. 208, 1997.
-
N. Kato and T. shigetomi, “Underwater Navigation for Long-Range Autonomous Underwater Vehicles Using Geomagnetic and Bathymetric Information,” Advanced Robotics, vol. 23, pp. 787-803, 2009.
[https://doi.org/10.1163/156855309X443016]

-
J. Jung, J. Park, and J. Choi, “Underwater Magnetic Field Mapping Using an Autonomous Surface Vehicle,” The Journal of Korea Robotics Society, vol. 13, no. 3, pp. 190-197, Sept., 2018.
[https://doi.org/10.7746/jkros.2018.13.3.190]

1993 서울대학교 조선해양공학 학사
1996 서울대학교 조선해양공학 석사
2007 Stanford University 항공우주공학 박사
1995~2000 한국기계연구원/한국해양연구원
선박해양공학연구센터(KRISO) 연구원/선임연구원
2007~2010 Optimal Synthesis Inc. Research Scientist
2010~현재 카이스트 기계공학과 부교수
관심분야: 해양로봇의 항법, 자율운항기술

![[Fig. 1] [Fig. 1]](/xml/26017/JKROS-15-1-24_F1.jpg)
![[Fig. 2] [Fig. 2]](/xml/26017/JKROS-15-1-24_F2.jpg)
![[Fig. 3] [Fig. 3]](/xml/26017/JKROS-15-1-24_F3.jpg)
![[Fig. 4] [Fig. 4]](/xml/26017/JKROS-15-1-24_F4.jpg)
![[Table 1]](../img/npr_tablethum.jpg)
![[Fig. 5] [Fig. 5]](/xml/26017/JKROS-15-1-24_F5.jpg)