원형 구조 알고리즘을 이용한 근전도 패턴 인식 및 분류

1. 서 론

최근 사물 인터넷(IoT) 및 인공지능(AI) 기술의 발달에 따라 근전 도(EMG: Electromyography) 및 심전도(ECG: Electrocardiogram) 등의 생체신호를 인간과 컴퓨터 사이의 인터페이스로서의 사 용가능성이 증대되고 있다. 그 중 근전도는 근육에 전달되는 신경과 자극을 전달받는 근섬유에서 나타나는 활동전위로부 터 발생된 전기 신호이며, 이는 절단 장애인을 위한 제어 수단 으로 다양한 연구들이 진행되고 있다^[1-3]. 근전도를 이용한 전 동 의수는 절단 부위에서 표면 근전도 신호를 취득하여 사용 자가 별다른 조작 없이 동작을 수행할 수 있도록 설계되어 있 다. 최근에는 기계학습(Machine learning)을 이용하여 실제 사 용자가 의도한 동작을 역으로 추론하는 알고리즘이 연구되고 있으며, 서포트 벡터 머신(Support Vector Machine, SVM), 다 층 퍼셉트론(Multi-layer Perceptron, MLP), 합성곱 신경망 (Convolution Neural Network, CNN), 순환 신경망(Recurrent Neural Network, RNN) 등의 학습 알고리즘을 이용한 패턴 분 류 방법들이 적용되어 왔다^[4,5].

대표적인 근전도 전동 의수에는 Touch Bionic의 i-Limb, Otto Bock의 Bebionic, Michelangelo 등이 있으며 근전도를 이 용한 다양한 손동작이 가능하다. 그러나 상용 전동 의수들은 주로 On-off 형식의 구동 시스템을 사용하고 있으며, 사용자들 은 이를 습득하기 위한 학습과정 및 시간이 필요하다. 이를 개 선하기 위해, 다채널 근전도 신호를 이용한 패턴 인식에 대한 연구들이 진행되고 있으나^[6,7], 고정된 위치에서 근전도 신호 가 측정되어야 하므로 위치가 변동될 때마다 새로운 데이터를 수집하고 학습하는데 많은 시간과 노력이 요구된다. 또한 기존 선행연구들의 경우, 개발된 의수의 기존 학습 방법을 사용하 거나, 여러 가지 기계학습 알고리즘에 대한 비교 연구가 진행 되어 왔으나, 전동 의수를 위한 팔 구조를 모방한 알고리즘 개 발 및 측정 위치에 관한 연구들은 미비한 실정이다.

따라서, 본 논문에서는 근전도 센서의 측정 위치에 상관없 이 원통 형상의 팔에서 근전도 신호의 특성을 반영한 원형 구 조 기반의 패턴 인식 및 분류 알고리즘을 제안한다. 근전도 센 서의 전극 위치를 무작위로 지정해도 동일한 패턴을 인식할 수 있고, 모든 채널의 데이터가 서로 연결되어 있는 원형 구조 (Circular structure)를 제안한다. 제안된 알고리즘의 성능 평가 를 위해, 3가지 지도 학습(Supervised learning)의 알고리즘에 적용하여 분류 가능성을 평가하고, 기존 선형 구조(Linear structure)와의 차이를 비교 분석함으로써 알고리즘의 실용성 과 상용화 가능성에 대하여 의의를 두는 바이다.

본 논문은 다음과 같이 구성된다. 2장에서는 원형 알고리즘 에 관한 데이터 수집 방법 및 분류 가능성을 평가하기 위해 적 용된 기계 학습 알고리즘을 설명한다. 3장에서는 제안된 방법 의 학습 환경 및 신경망을 통한 패턴 분류 실험 결과를 설명하 며, 4장에서는 본 연구에 대한 요약과 결론 및 추후 연구 방향 에 대해 기술한다.

2. 원형 구조 알고리즘 제안

2.1 원형 구조 기반 데이터 수집

2.1.1 근전도 신호 처리 과정

전완의 둘레에서 측정된 8채널의 데이터는 [Fig. 1]과 같이 특징점 추출과 정규화 과정을 통해 기계 학습에 적용 가능한 학습 데이터로 생성된다. 근전도 신호의 특징점 추출은 Root mean squaring (RMS), Zero crossing (ZC), Mean absolute value (MAV), Slope sign change (SSC)와 같이 시간 영역에서 사용되는 다양한 방법들이 있으며^[5], 본 연구에서는 비교적 계산이 간단하 고 우수한 성능을 보이는 다음 식과 같은 RMS를 사용하였다.

[Fig. 1]

Surface electromyography signal processing

$\[ x_{rms,i}\left(k\right)=\sqrt{\frac{1}{N}{\displaystyle {\sum }_{n=1}^N{x}_i{\left(k-n+1\right)}^2}} \]$

(1)

여기에서 N은 데이터 윈도우의 크기, x_i(k)는 i번째 채널에 서 k번째 sampling time에 측정된 sEMG 데이터이다. 각 채널 의 값은 N개씩 제곱하여 더해진 후에 평균을 취하고 이어서 제곱근 연산을 수행하여 RMS값 x_{rms, i} (k)으로 구해진다. 추 출된 특징은 항상 0 이상의 값을 가지며 네트워크에 적용하기 쉽게 만들기 위해 0과 1 사이로 정규화 하였다^[8]. 정규화는 최 소-최대 방법을 사용하였고 다음 식을 통해 얻어진다.

$\[ x_{n,i}\left(k\right)=\frac{x_{rms,i}\left(k\right)-x_{min,i}}{x_{max,i}-x_{min,i}} \]$

(2)

여기서 x_n,i (k)는 k번째의 정규화 데이터를 의미하며 x_{min, i} 은 휴식 상태에서 i번째 채널 RMS 값 중 최소값, x_max,i는 실 험자가 주먹 상태에서 낼 수 있는 최대 힘을 주어 얻은 MVC (Maximum voluntary contraction)에서의 최대 RMS 값이다.

2.1.2 원형 구조 알고리즘

정규화된 데이터는 네트워크의 학습 데이터로 생성 된다. 일반적인 데이터 세트는 [Fig. 2]와 같은 선형 구조로 각 채널 의 데이터가 순차적으로 나열되어 있고, 채널1과 채널8의 데 이터가 연결되어 있지 않은 형태를 나타낸다. 반면에, 본 논문 에서 제안하는 알고리즘은 [Fig. 3]과 같이 원형 구조를 가지는 데이터를 이용하여 패턴을 분류하였다. 제안하는 원형 구조에 서는 원형 연결 리스트(Circular linked list) 구조를 적용하였다 ^[9-12]. 이는 [Fig. 3]과 같이 첫 노드(Node)와 마지막 노드가 연결 되어 원형 구조를 이룬다. 따라서 각 채널 사이의 구분이 사라 지기 때문에 전극의 위치를 무작위로 위치시켜도 동일하게 동 작을 분류하도록 설계하였다.

[Fig. 2]

Dataset with linear structure

[Fig. 3]

Dataset with circular structure

제안된 방법은 선입선출(First-in First-out)을 이용하여 채널 1의 데이터부터 순차적으로 입력되며 8개 채널의 근전도 신호를 시계방향으로 시프트(Shift) 시켜 사용하여 원형 구조를 유지 한다. 회전된 채널은 8번 반복된 후에 처음 채널의 위치로 돌 아오게 된다.

2.2 기계학습 알고리즘

근전도 신호의 패턴 분류 방법은 [Fig. 4]의 과정을 따른다. 신호 처리 과정을 거쳐 생성된 원형 구조 학습 데이터는 다층 퍼셉트론(MLP), 합성곱 신경망(CNN), 장단기 메모리 신경망 (LSTM)의 네트워크에 각각 적용되어 분류 결과를 비교 분석 하고, 학습을 마친 네트워크를 검증하기 위해 원형 구조 근전 도 신호를 테스트 데이터로 사용하여 패턴 인식 및 분류 결과 를 확인하였다.

[Fig. 4]

Schematic diagram of pattern classification

2.2.1 다층 퍼셉트론(MLP)

다층 퍼셉트론은 입력층(Input layer), 은닉층(Hidden layer), 출 력층(Output layer)으로 구성되며, 모든 노드가 연결된 전 방향 (Feedforward) 신경망이다^[13]. 활성 함수를 가지는 노드는 가중치 를 가지고 연결되며 가중치를 조절하여 목푯값을 추정한다. 가중 치는 오류 역전파 알고리즘(Backpropagation)을 이용하여 출력과 목푯값이 허용될 오차 보다 클 경우 반복적으로 학습된다^[14].

사용된 입력층의 노드에는 근전도 센서의 8채널에서 측정 되는 근전도 신호에 대해서 RMS와 정규화를 거쳐서 생성되 는 신호들이 적용되며, 출력층의 노드는 실험에 사용된 5가지 의 동작으로 구성된다. 사용된 MLP는 [Fig. 5]와 같이 은닉층 1 개에 128개의 노드를 가지며 활성 함수로 ReLU (Rectified linear unit)함수를 사용하였다. MLP의 입력층 노드 개수를 i, 은닉층 노드 개수를 j, 출력층 노드 개수를 k라고 가정할 때, 은닉층의 j째 노드 h_j이며, 식은 다음과 같다.

[Fig. 5]

Structure of multi-layer perceptron (MLP)

$\[ h_j={\displaystyle {\sum }_i{w}_{ij}{u}_i} \]$

(3)

여기서 w_ij는 입력층의 i번째 노드와 은닉층의 j번째 노드를 연결하는 가중치(Weight)를 의미하며 u_i는 입력층의 i번째 노 드의 입력 값인 i번째 채널의 RMS와 정규화를 거친 근전도 신 호이다. 은닉층 노드 h_j는 다음 식과 같은 Softmax 함수를 거 쳐 출력층의 입력으로 사용되고 출력 값 y_k 식은 다음과 같다.

$\[ y_k=\frac{e^{h_j}}{{\displaystyle {\sum }_{j=1}^n{e}^{h_j}}} \]$

(4)

여기서 y_k는 학습 데이터의 목표 값과 함께 특정한 목적함수 에 적용되어 오차를 생성하게 되며, 이를 최소화하도록 MLP 를 반복 훈련시킨다. 본 연구를 위해서 목적함수로는 교차-엔 트로피 오차(Cross-entropy error)가 사용되었다.

$\[ E=-{\displaystyle {\sum }_k{t}_k\text{log}{y}_k} \]$

(5)

여기서 t_k는 실제 레이블(Label)이며 데이터를 중복 없이 표현 하기 위해 원-핫 인코딩(One-hot encoding) 방법을 사용하였 다. 원-핫 인코딩은 목표 동작에 대한 값은 1이고 나머지는 모 두 0으로 표시하는 방법이며, 예를 들어, 첫번째 동작인 주먹 (grasping)은 [1,0,0,0,0]와 같이 나타낸다.

2.2.2 합성 곱 신경망(CNN)

합성 곱 신경망(Convolution Neural Network, CNN)은 이미 지 분류에 주로 활용되는 신경망으로 입력 이미지(Input image) 에 합성 곱(Convolution) 연산을 사용하여 특징(Feature)을 추 출하는데 사용된다^[15]. 다음의 식은 2차원 구조에서의 합성 곱 연산을 의미하며 x는 입력 이미지, y는 출력, w는 가중치, [m,n]은 픽셀(Pixel) 좌표, k는 커널 사이즈를 의미한다.

$\[ \begin{array}{c}y\left[i,j\right]=\left(x*w\right)\left[i,j\right]\\ ={\displaystyle \sum _{i=0}^k{\displaystyle \sum _{j=0}^{k}x\left[m-i,n-j\right]w\left[m,n\right]}}\end{array} \]$

(6)

합성 곱 신경망에 사용할 이미지를 만들기 위해, 8채널의 근 전도 신호를 측정하여 RMS와 정규화 처리를 거쳐서 8개의 샘 플을 8×8의 입력 이미지로 생성하였다. 입력 이미지는 합성 곱 을 수행하기 위해 1×3×16×16의 텐서(Tensor)로 변환되었다. 커널을 통과하기 위해 이미지 크기를 재조정하였는데, 이때 방 식은 픽셀 간의 영역 평균(Area averaging)을 이용하였다. 또한, 기존의 흑백 이미지를 3개 겹쳐 RGB 크기의 이미지로 만들어 사용하였다. 이후 입력 이미지는 합성 곱 계층(Convolutional layer), 최대 풀링 계층(Max pooling layer), 전 연결 계층(Fullyconnected layer)을 통과하여 5개의 출력값으로 변환하였다.

CNN의 전체적인 구조는 [Fig. 6]과 같다. 합성 곱 계층은 총 3개의 레이어를 사용하였고 첫 번째 층과 두 번째 층의 커널 (Kernel) 크기는 3이고 세 번째 층의 커널 크기는 2로 설정하였 다. 최대 풀링 계층에서는 2x2 픽셀 크기에서 가장 큰 값을 선 택하여 텐서의 크기를 줄였고, 모든 전 연결 계층은 드롭-아웃 (Drop-out) 기법과 활성화 함수인 ReLU 함수를 사용하여 64개 의 출력을 5개의 출력값으로 변환시켰다. 이렇게 5개의 출력 값은 argmax 함수를 사용하여 가장 큰 인수를 찾는다. 이 인수 는 합성 곱 신경망을 통해 분류된 동작을 의미한다.

[Fig. 6]

Structure of convolution neural network (CNN)

2.2.3 장단기 메모리 신경망(LSTM)

장단기 메모리 신경망(Long short-term memory, LSTM)은 현재 입력 시퀀스 x_t, 직전 은닉층 출력인 h_t–1가 필요하다. LSTM 셀(Cell)은 직전 상태 h_t–1와 입력 x_t에 대해 4개의 내 부 레이어를 가진다. 내부 레이어는 망각 게이트(Forget gate), 입력 게이트(Input gate), 업데이트 게이트(Update gate), 출력 게이트(Output gate)로 구성되어 있다^[16]. 입력 시퀀스는 센서 의 8채널 원형 구조 데이터 세트를 의미하며 현재 상태는 동작 의 패턴이 된다. LSTM의 전체 구조는 [Fig. 7]과 같다.

[Fig. 7]

Structure of long short-term memory (LSTM)

망각 게이트는 셀로부터 어떤 동작의 패턴 정보를 버릴 것 인지 정하며 시그모이드 레이어에 의해 결정된다. h_t–1와 x_t 를 입력받아 0과 1 사이의 값이 y_t–1로 보내진다. 여기서 U_ƒ는 입력층에서 은닉층으로 갈 때의 가중치이며 W_ƒ는 은닉층과 은닉층을 연결하는 순환 노드의 가중치를 의미한다. 망각 게 이트는 다음과 같다.

$\[ f_t=\sigma \left(U_f{x}_t+W_f{h}_{t-1}+b_f\right) \]$

(7)

입력 게이트는 앞으로 들어올 새로운 패턴 중 어떤 데이터 를 셀에 저장할지를 결정하며, 시그모이드 레이어가 업데이트 할지 선택한다. 하이퍼볼릭 탄젠트(Hyperbolic tangent) 레이 어가 새로운 후보 값인 y_t라는 벡터를 만들어 셀에 더하고 두 단계에서 나온 정보를 합쳐 상태를 업데이트하게 된다.

$\[ i_t=\sigma \left(U_i{x}_t+W_i{h}_{t-1}+b_i\right) \]$

(8)

$\[ {\tilde{y}}_t=\text{tanh}\left(U_f{x}_t+W_f{h}_{t-1}+b_y\right) \]$

(9)

과거 상태인 y_t–1를 업데이트해서 새로운 셀 상태인 y_t를 만든 다. 이전 상태의 ƒ_t를 곱해서 가장 첫 단계에서 잊은 정보를 제거한 후 $$ x_t*{\tilde{y}}_t$$ 를 더하여 업데이트하는 값을 얼마나 수행할지 지정한 만 큼 스케일링 한 값이 된다. 업데이트 게이트는 다음 식과 같다.

$\[ y_t=f_t*y_{t-1}+x_t*{\tilde{y}}_t \]$

(10)

마지막으로 출력 게이트는 어떤 패턴을 출력으로 내보낼지 결정한다. 먼저, 시그모이드 레이어에 입력 데이터를 사용하 여 셀의 어느 부분을 출력으로 결정할지 정한 후 하이퍼볼릭 탄젠트 레이어를 거쳐 -1과 1 사이의 값을 출력하고, 시그모이 드 게이트의 출력과 곱하여 원하는 출력 값만 얻는다. 출력은 다음 식을 통해 얻는다.

$\[ o_t=\sigma \left(U_o{x}_t+W_o{h}_{t-1}+b_o\right) \]$

(11)

$\[ h_t=o_t*\text{tanh}\left(y_t\right) \]$

(12)

3. 실험 및 결과

3.1 실험 대상 및 학습 환경

본 연구는 한양대학교 기관 생명윤리위원회(Institutional Review Board: IRB)에서 2019년 7월(HYI-16-0550-8) 최종 승인을 받은 후에 진행하였다. 연구 대상은 신체 건강한 성인 남녀 3명(남성 2 명, 여성 1명)으로 선정하였고, 연구의 목적 및 실험 절차에 대하 여 실험 참여자에게 충분한 설명을 제공한 후 진행하였다.

본 실험은 전완에 대한 원형 구조의 데이터 세트를 생성하 기 위하여 근전도 센서(MYO, Thalmic Labs)를 사용하였다. MYO 센서는 8개의 전극으로 구성되어 있고 8bit의 분해능과 200 Hz의 샘플링 속도를 가지며 측정 위치는 손과 손목의 움 직임과 관련이 있는 전완에 위치하도록 착용하였다. 전완의 근육에는 손 동작에 관여하는 지신근(extensor digitorum)과 손 목 동작에 관여하는 요측수근굴근(radial flexor of wrist), 장장 근(palmaris longus) 등이 있으며, 근육의 움직임은 동작에 의 해 생성되는 근전도 패턴과 밀접한 관계를 가진다^[3]. 따라서, 근전도 센서를 손과 손목의 동작과 관련된 근육 부위에 착용 한 후, 서로 다른 특징의 패턴을 생성하기 위하여 [Fig. 8]과 같 이 주먹(Grasping), 굴곡 및 신전(Flexion-Extension), 회외와 회 내(Supination-Pronation)의 5가지 목표 동작을 선정하였다. 실 험 데이터 획득은 한 동작에 대하여 약 20초 동안 수행하였다. 측정 데이터는 밴드 패스 필터(Band-pass Filter of 8~200 Hz) 와 노치 필터(60 Hz)를 적용 한 후 300 ms 윈도우 크기를 갖는 RMS를 이용하고 정규화를 적용하였다.

[Fig. 8]

Five target postures for pattern classification

이러한 방법으로 [Fig. 9(a)]와 같이 고정된 위치에서의 학습 데이터 세트 1개와 [Fig. 9(b)]와 같이 시계 방향으로 전극 채널을 회전시켜 임의로 정한 위치에서의 학습 데이터 2개에 대하여 총 5번 반복 측정하였다. 생성된 학습 데이터들은 각각의 네트워크 에 적용되어 패턴 분류를 위한 학습과정을 수행하게 된다.

[Fig. 9]

MYO band sensor and wearing location: (a) fixed location (b) varying location

실험은 크게 두 부분으로 나누어진다. 첫 번째는 전극 채널을 회전시키며 서로 다른 위치에서 반복 측정 된 선형 구조와 원형 구조의 데이터에 대하여 패턴 인식을 수행한 후 결과를 분석한 다. 두 번째로는 MLP, CNN, LSTM의 기계학습 알고리즘에 적 용하여 두 가지 구조의 분류 정확도에 대하여 비교 분석한다.

3.2 실험 결과

3.2.1 선형 구조와 원형 구조의 반복 측정 분석

기존 선형 구조와 제안된 원형 구조의 반복 측정 데이터를 비교 분석하기 위해, 주먹 동작에 대하여 5회 반복 측정하였으 며, 그 결과는 [Fig. 10]과 같다. [Fig. 10]은 8개의 채널에서 얻 어진 데이터를 8×8의 이미지를 비교한 것이다. 한 줄의 데이터 는 8개의 채널 중 가장 큰 값과 가장 작은 값을 선별하여 정규 화 하였으며 큰 값은 흰색 작은 값은 검은색으로 표현하였다.

[Fig. 10]

Pattern image: (a) linear (b) circular

[Fig. 10(a)]는 선형 구조 데이터로 각 채널에 위치한 근육의 활성화 유무를 알 수 있으나, 임의의 위치에서 반복 측정하였 을 경우 위치가 변화함에 따라 각 채널의 근전도 증폭에 대한 차이로 패턴이 변화됨을 확인할 수 있었다. 반면에, [Fig. 10(b)]는 원형 구조 데이터로 5회 반복 측정한 결과 유사한 패 턴이 생성됨을 확인하였다.

[Fig. 11]은 5개의 목표 동작에 대하여 선형 구조와 원형 구 조의 패턴과 상자 그래프(Box plot)이다. [Fig. 11(a)]는 선형 구 조의 결과로 각 동작에 대해 특정 채널의 값이 증폭되며 상자 그래프에서 증폭된 채널이 높게 나타나는 데이터의 분포를 확 인할 수 있었다. [Fig. 11(b)]에서는 원형 구조의 결과로 각 채 널의 최댓값과 최솟값, 그리고 중앙값이 모두 동일한 데이터 의 분포가 나타난다.

[Fig. 11]

Five target postures for pattern recognition and box plot: (a) linear structure (b) circular structure

따라서, 원형 구조는 반복 측정하였을 때 유사한 패턴이 나 타나며, 5가지에 대한 각 동작의 패턴에 대하여 명확한 차이를 확인하였다. 이를 통해 일상생활 활동을 위해 근전도 전동 의 수의 착용하는 경우 기존에 한번 학습이 이루어졌다면, 전극 채널 위치 변경에 따라 다시 학습을 수행할 필요가 없다. 이를 통해 제안된 원형 구조 방법의 목표 동작에 대한 반복성 및 실 용 가능성을 확인할 수 있었다.

3.2.2 선형 구조와 원형 구조의 분류 정확도 비교

선형 구조와 원형 구조의 분류 정확도를 비교하기 위하여, 기계학습 방법인 MLP, CNN, 그리고 LSTM 네트워크에 적용 하였다. 분류를 위한 동작은 [Fig. 8]과 같이 주먹, 굴곡, 신전, 회외, 회내의 순서로 수행되었다. Learning rate는 0.001로 설 정하였고 Epoch는 300회 반복 학습하였다.

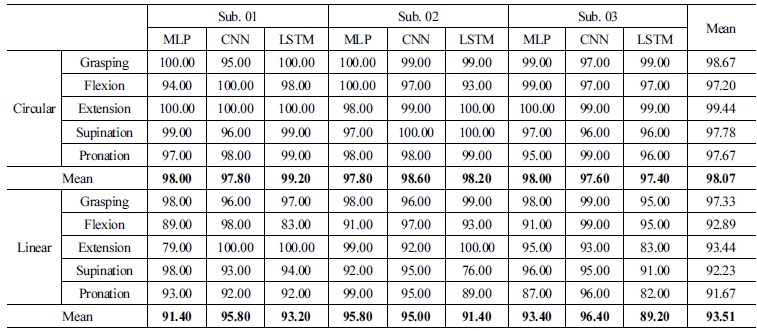
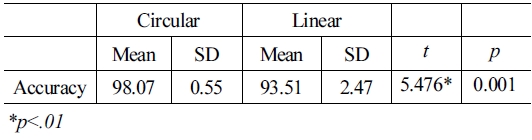
[Table 1]은 3명의 피험자에 대한 3가지 네트워크의 패턴 분 류 실험을 실시한 결과이다. 각 동작 당 5,000개의 데이터를 측 정하였으며, 전체 데이터 세트는 총 25,000개이다. 각 동작에 대한 원형 구조 인식률에서는 신전 동작이 99.44%로 가장 높 게 나타났으며, 선형 구조에서는 주먹 동작에서 97.33%로 가 장 높은 인식률을 보였다. 이는 원형 구조의 주먹 동작과 비교 했을 때 약 1.3% 낮게 나타났다. 추가적으로 원형 구조와 선형 구조의 정확도의 차이에 대하여 [Table 2]와 같이 대응 표본 t- 검정을 통해 분석하였다. 그 결과 원형과 선형 구조의 정확도 에 있어서 유의한 차이를 보였다(p<.01). 전체 피험자에 대한 원형 구조의 인식률은 평균 98.07% 이며, 선형 구조의 평균 인 식률(93.51%) 보다 약 4.6%의 높은 인식률이 나타났다.

[Table 1]

Experimental results of three subjects

[Table 2]

Results of the paired t-test analysis

더 나아가 전체 피험자의 75,000개(=25,000×3명) 데이터 세 트를 3가지 네트워크에 적용하여 패턴 분류 실험을 실시하였 다. 결과는 [Fig. 12]와 같으며 MLP, CNN, 그리고 LSTM에서 모두 원형 구조의 분류 정확도가 더 높게 나타났음을 확인하 였다. 특히, MLP 네트워크에서 정확도의 차이가 약 4%로 가 장 크게 나타났다.

[Fig. 12]

Comparison of classification accuracy regarding three subjects

4. 결 론

본 연구는 근전도 센서의 착용 위치에 제한을 두지 않고 원 통형의 팔에서 측정되는 신호의 특성을 반영하여 원형 구조 기반의 패턴 인식 및 분류 알고리즘을 제안하였다. 원형 구조 의 데이터 수집 방법은 센서의 채널 위치를 임의로 지정해도 동일한 패턴으로 인식할 수 있도록 모든 채널이 원형으로 서 로 연결되어 있는 형태를 유지한다. 이렇게 제안된 원형 구조 의 성능을 평가하기 위하여, 기존의 선형 구조와의 비교 분석 을 실시하였다.

첫째, 원형 구조와 선형 구조의 학습 데이터를 이용한 패턴 인식을 실시하였으며, 각각 다른 위치에서 3번 반복 측정하였 다. 그 결과, 선형 구조의 데이터는 같은 동작에 대하여 반복 측정 시 다른 패턴이 생성되었지만, 원형 구조는 유사한 형태 의 패턴이 생성되었다. 또한, 5개의 목표 동작에 대해서는 서 로 다른 패턴이 뚜렷하게 나타났으며 이는 수행할 수 있는 손 동작에 대하여 다양한 패턴 인식이 가능함을 확인할 수 있었 다. 둘째, 3명의 피험자에 대하여 지도학습 알고리즘인 MLP, CNN, LSTM에 대해서 적용 실험을 실시하였다. 그 결과 3개 의 네트워크에서 원형 구조의 높은 분류 정확도를 확인하였 고, LSTM에서 가장 큰 차이를 보였다. 이처럼 기존의 데이터 수집에 사용되는 선형 구조의 패턴 분류 알고리즘은 실제 의 수 사용자의 경우, 정확한 측정 위치에서 사용이 가능하다는 현실적인 어려움을 갖게 된다. 또한, 실제 사람의 팔에 착용하 는 근전도 센서는 원형 구조를 가지며 센서의 각 채널에서 출 력되는 데이터는 양 끝이 이어져 있어 서로 다른 채널에도 영 향을 미친다. 기존의 선형 구조의 데이터는 이러한 특성을 표 현하지 못하며 양 끝의 채널 사이의 근전도 신호의 관계를 무 시한다는 것 또한 한계점으로 작용한다.

본 연구는 근전도 전동 의수의 구동 시스템 개발뿐만 아니 라 재활 및 웨어러블 로봇 분야로 확대될 수 있다. 또한 앞으로 의 후속 연구에서는 전동 의수와 제안된 알고리즘을 통합하여 실시간 제어가 가능한 의수 개발하는 것이 목표이다.

Acknowledgments

This work was supported by the convergence technology development program for bionic arm through the National Research Foundation of Korea (NRF) funded by the Ministry of Science & ICT (No. 2015M3C1 B2052811).

References

• M. A. Oskoei and H. Hu, “Myoelectric control systems-A survey,” Biomedical Signal Processing and Control, vol. 2, no. 4, pp. 275-294, 2007. [https://doi.org/10.1016/j.bspc.2007.07.009]
• M. Ferdjallah, J. J. Wertsch, and G. F. Harris, “Effects of surface electrode size on computer simulated surface motor unit potentials,” Electromyography and Clinical Neurophysiology, vol. 39, no. 5, pp. 259-265, 1999.
• Y.-J. Kim, D.-H. Lee, H. Park, J.-H. Park, J.-H. Bae, and M.-H. Baeg, “Wrist and Grasping Forces Estimation using Electromyography for Robotic Prosthesis,” The Journal of Korea Robotics Society, vol. 12, no. 2, pp. 206-216, Jun., 2017. [https://doi.org/10.7746/jkros.2017.12.2.206]
• M. Pontil and A. Verri, “Properties of support vector machines,” Neural Computation, vol. 10, no. 4, pp. 955-974, 1998. [https://doi.org/10.1162/089976698300017575]
• A. Hiraiwa, K. Shimohara, and Y. Tokunaga, “EMG pattern analysis and classification by neural network,” Conference Proceedings, IEEE International Conference on Systems, Man and Cybernetics, Cambridge, USA, pp.1113-1115, 1989.
• S. Lee, M.-O. Kim, T. Kang, J. Park, and Y. Choi, “Knit Band Sensor for Myoelectric Control of Surface EMG-based Prosthetic Hand,” IEEE Sensors Journal, vol. 18, no. 20, Oct., 2018. [https://doi.org/10.1109/JSEN.2018.2865623]
• Y. Jiang, M. Togane, B. Lu, and H. Yokoi, “sEMG Sensor Using Polypyrrole-Coated Nonwoven Fabric Sheet for Practical Control of Prosthetic Hand,” Frontiers in Neuroscience, vol. 11, no. 33, Feb., 2017. [https://doi.org/10.3389/fnins.2017.00033]
• A. Phinyomark, P. Phukpattaranont, and C. Limsakul, “Feature reduction and selection for EMG signal classification,” Expert Systems with Applications, vol. 39, no. 8, pp. 7420-7431, 2012. [https://doi.org/10.1016/j.eswa.2012.01.102]
• J. Sola and J. Sevilla, “Importance of input data normalization for the application of neural networks to complex industrial problems,” IEEE Transactions on Nuclear Science, vol. 44, no. 3, pp. 1464-1468, 1997. [https://doi.org/10.1109/23.589532]
• J. E. Hopcroft and J. D. Ullman. Data structures and algorithms. 1983.
• M. M. Michael and M. L. Scott, “Simple, Fast, and Practical Non-Blocking and Blocking Concurrent Queue Algorithms,” Proc. 15^thAnn. ACM Symp. Principles of Distrubuted Computing, pp. 267-275, May, 1996. [https://doi.org/10.1145/248052.248106]
• C. D. Kasper. “Method and network device for creating circular queue structures in shared memory,” U.S. Patent No. 6,526,451. 25 Feb., 2003.
• M. W. Gardner and S. R. Dorling. “Artificial neural networks (the multilayer perceptron)-a review of applications in the atmospheric sciences,” Atmospheric Environment, vol. 32, no. 14-15, pp. 2627-2636, 1998. [https://doi.org/10.1016/S1352-2310(97)00447-0]
• R. Hecht-Nielsen. “Theory of the backpropagation neural network,” Neural Networks for Perception, Academic Press, 1992. pp. 65-93. [https://doi.org/10.1016/B978-0-12-741252-8.50010-8]
• A. Krizhevsky, I. Sutskever, and G. E. Hinton. “Imagenet classification with deep convolutional neural networks,” Advances in Neural Information Processing Systems, 2012.
• S. Hochreiter and J. Schmidhuber. “Long short-term memory,” Neural Computation, vol. 9, no. 8, pp. 1735-1780, 1997. [https://doi.org/10.1162/neco.1997.9.8.1735]