외벽청소로봇(ROPE RIDE)의 등강 로봇 플랫폼을 위한 로프 모델링 및 검증

1. 서 론

고층 빌딩이 증가함에 따라 빌딩 외벽의 청소, 보수, 유지 등 의 관리 업무에 대한 필요성도 증가하고 있다. 대부분의 고층 빌딩의 경우 외벽의 유지 보수를 위한 곤돌라가 설치되어 있 는데 곤돌라가 설치되어 있지 않은 빌딩의 경우 로프공이 옥 상에 로프를 고정한 후 로프에 연결된 간이 의자를 타고 내려 오면서 작업을 수행하게 된다. 로프공은 별도의 안전장치 없 이 로프에만 몸을 의지하기 때문에 항상 추락의 위험에 노출 되어 있어 국내에서만 연간 안전사고 사상자가 15명에 이를 정도로 고위험 직업군에 속한다.

이러한 고소 작업을 대체하기 위하여 다양한 등반로봇들이 개발되고 있다. TITO500의 경우 옥상에 있는 크레인에 의해 등 하강이 가능하며 옥상에 있는 레일을 통하여 크레인이 좌우로 움직이는 구조를 가지고 있다^[1]. SIRIUSc또한 옥상의 크레인을 이용하여 등 하강하며 작업시 로봇의 안정성을 확보하기 위하 여 흡착 패드 구조를 사용한다^[2]. BFMR은 건물 외벽 프레임에 빌트인 구조의 레일을 설치함으로써 레일을 따라 상하좌우의 이동을 하며 건물의 등 하강을 위해 크레인을 이용한다^[3]. 이 외 에도 건물 외벽에서의 작업을 위해 다양한 로봇이 연구되었으 나 모두 건물 옥상에 크레인과 같이 로봇을 등하강시키기 위한 구조물이 별도로 필요하며 실제 외벽에 존재하는 다양한 형상 의 장애물을 극복하는 것이 어려운 한계점을 가지고 있다.

본 논문에서 제시하는 외벽청소로봇(ROPE RIDE)는 로프 공이 사용하는 로프를 이용하여 등 하강을 하며 삼각 트랙을 이용하여 장애물을 극복한다^[4]. ROPE RIDE는 옥상에 연결된 로프만 있으면 사용이 가능하기 때문에 크레인이 설치되어 있 지 않은 빌딩에 폭넓게 사용이 가능하며, 삼각 트랙을 통해 장 애물을 등반 가능하기 때문에 다양한 빌딩에 적용할 수 있다.

ROPE RIDE가 외벽에서의 작업을 안정적으로 수행하기 위 해서는 로봇의 등 하강 속도를 일정하게 유지하는 것이 필요 한데, 본 로봇이 사용하는 나일론 재질의 등반 로프의 경우 신 장률이 30%에 이르기 때문에 로프의 움직임을 예측하는 것이 힘들다. 또한 로프의 경우 같은 재질의 심선을 사용하더라도 심선이 꼬여있는 패턴, 로프의 두께, 로프에 부가되는 질량 등 에 따라 특성이 달라지기 때문에 사용하는 조건에 맞는 특성 을 파악하는 것이 중요하다.

섬유 로프를 모델링하는 일반적인 방법은 길이의 변화에 따라 특성이 변하는 로프의 특성을 스프링과 댐퍼의 다양한 조합으로 표현하는 것이다^[5]. PLA-PCL섬유의 크리프 및 응력 완화 특성을 실험을 통하여 모델링하는 방법에 대한 연구가 소개되었으며^[6], 주파수 응답 실험을 통해 합성섬유의 동 특성 을 파악하는 연구가 진행되었다^[7].

본 논문은 외벽청소로봇의 이동 특성을 모델링하기 위한 기초 연구로써 등반 로프의 구조를 스프링, 댐퍼의 조합으로 모델링하고 실험을 통해 특성 값을 찾는 연구를 수행하였다. 선행 연구들은 로프의 특성을 확인하기 위해서 대부분 1m 미 만의 로프 시편으로 인장 실험을 수행하였지만 본 논문에서는 22.5m의 로프 사용하여 실제 외벽 청소 로봇이 외벽에 매달린 상황과 같은 조건으로 실험을 수행하였다. 또한 나일론 재질 의 등반 로프의 특성과 다양한 두께에 따른 특성 변화에 대한 연구를 수행하여 ROPE RIDE뿐만 아니라 등반 로프를 적용 가능한 다른 로봇의 모델링에도 활용될 수 있다.

본 논문의 2장에서는 ROPE RIDE의 구조와 동작원리를 소 개하고 3장에서는 단위 계단 입력과 크리프 예비 실험을 통해 유도한 로프의 모델에 대해서 소개한다. 4장에서는 로프의 모 델을 구하기 위한 테스트벤치를 소개하고 실험을 통해 모델링 의 파라미터를 구한다.

2. ROPE RIDE의 구조 및 동작원리

본 논문에서 제안하는 ROPE RIDE의 구조는 [Fig. 1]과 같 다. ROPE RIDE는 로프 등강기, 삼각 트랙 및 프로펠러 추력기 를 핵심 요소로 가지고 있으며 경로가 틀어졌을 경우 진행방 향을 변경할 수 있는 조향축을 가지고 있는 것이 특징이다.

[Fig. 1]

Kinematic structure of ROPE RIDE

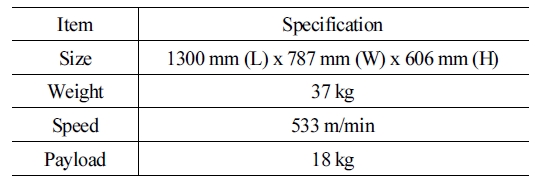
로프 등강기의 경우 V자 쐐기 형상의 그루브를 갖는 등강 용 풀리를 이용하여 로프가 이탈하지 않도록 고정한 상태에서 모터를 이용하여 회전시킴으로써 등반 및 하강을 가능하게 한 다. 이 때 ROPE RIDE가 벽면에서의 흡착력을 잃지 않고 안정 적으로 붙어 있게 하기 위해서 로봇의 위 아래에 프로펠러 추 력기를 배치하였으며 이 추력기들은 로봇이 작업하는 동안 전 도되지 않고 벽면에 붙어있을 수 있도록 한다. 4개의 삼각 트 랙은 로봇이 등 하강하는 동안 100 mm 이하의 장애물을 만나게 되면 수동적으로 회전함으로써 장애물을 극복 가능하다. 로봇의 제원은 [Table 1]에 정리되어 있다.

[Table 1]

Specifications of ROPE RIDE

3. 등반 로프 모델링

3.1 로프 모델링 예비 실험

이 절에서는 두 가지의 예비실험을 통하여 로프를 스프링, 댐퍼의 조합으로 모델링한다.

첫번째는 등강기를 이용하여 등가속도 구간 이후 등속도로 움직이도록 하는 속도 프로파일을 만들고, 이 때 등강기의 위 치를 측정함으로써 로프의 거동을 추정하는 실험이다. 실험 테스트벤치는 아래 [Fig. 2]와 같으며 실험결과는 [Fig. 3]과 같 다. 본 실험에서는 등속구간으로 전환되었을 때 로프는 위아 래로 흔들림과 동시에 진폭이 0으로 수렴하는 현상을 확인할 수 있다. 따라서 로프는 스프링과 댐퍼가 병렬로 연결된 Kelvin-Voight model로 가정할 수 있으며 부족 감쇄의 특성을 가지고 있음을 확인할 수 있다.

[Fig. 2]

Testbench for rope ascender

[Fig. 3]

Rope ascender test results

등반 로프의 크리프 특성을 확인하기 위하여 [Fig. 4]의테스 트벤치를 설계하였다. 본 실험은 로프를 눌러 고정한 상태에 서 인장시험기를 이용하여 로프에 인장력을 가하였으며 시간 이 지남에 따라 힘이 변화하는 정도를 측정하였다. 실험 결과 는 [Fig. 5]와 같으며 10분동안 장력이 감소하다가 평형상태에 도달하는 것을 확인할 수 있다. 따라서 본 등반 로프는 점 탄성 특성을 갖는 것을 확인할 수 있으며 크리프 현상은 스프링과 댐퍼가 직렬로 연결된 Maxwell model로 가정할 수 있다^[8].

[Fig. 4]

Testbench for rope tension test

[Fig. 5]

Rope tesion test results

3.2 로프의 구성 방정식 모델링

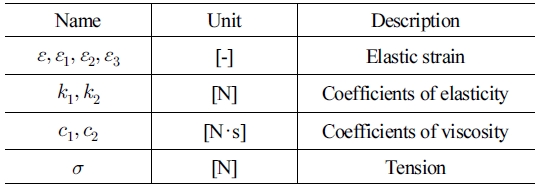
3.1절의 예비 실험 결과를 통해 등반 로프는 Kelvin-Voight 모델과 Maxwell 모델을 선형 조합한 Burgers 모델 혹은 Four element 모델로 가정할 수 있으며 이 때 모델의 도식도는 [Fig. 6] 과 같고 그 때의 구성 방정식(Constitutive equation)은 ‘식 (1)’ 과 같다^[8]. 이 때의 각 기호가 의미하는 바는 [Table 2]와 같다.

[Fig. 6]

Burgers model (Four element model)[8]

[Table 2]

Symbols and units in [Fig. 6]

$\[ \sigma +\left(\frac{c_1}{k_1}+\frac{c_1}{k_2}+\frac{c_2}{k_2}\right)\dot{\sigma }+\frac{c_1{c}_2}{k_1{k}_2}\ddot{\sigma }=c_1\dot{\epsilon }+\frac{c_1{c}_2}{k_2}\ddot{\epsilon } \]$

(1)

초기상태에서 인장력이 작용하지 않는 상태에서는 변형률 도 없으므로 σ(t)와 ε(t)의 라플라스 변환을 각각 $$ \widehat{\sigma }\left(s\right),\widehat{\epsilon }\left(s\right)$$ 라 할 때 ‘식 (1)’로부터 다음과 같은 관계식을 얻을 수 있다.

$\[ \begin{array}{l}\frac{\widehat{\epsilon }\left(s\right)}{\widehat{\sigma }\left(s\right)}=\frac{b_0{s}^2+b_{1}s+b_2}{s^2+a_{0}s}\\ \left(a_0=\frac{k_2}{c_2},b_0=\frac{1}{k_1},b_1=\frac{c_1{k}_1+c_1{k}_2+c_2{k}_1}{k_1{c}_1{c}_2},b_2=\frac{k_2}{c_1{c}_2}\right)\end{array} \]$

(2)

4. 모델링 파라미터 추정 실험

본 절에서는 3절에서 구한 구성방정식의 파라미터를 구하 기 위하여 4종류의 등반 로프를 실제 로봇 사용환경에 맞추어 실험을 진행하였다. 서울대학교 정밀기계공동연구소의 외벽 에서 실험을 진행하였으며 테스트벤치의 구조는 [Fig. 7]과 같 고 실험 모습은 [Fig. 8]과 같다. 실험에 사용된 로프의 전체 길 이는 22.5 m이며 직경 6 mm, 7 mm, 9 mm, 11 mm인 상용 나일 론(폴리아미드) 로프를 사용하였다.

[Fig. 7]

Testbench for rope elongation test

[Fig. 8]

Experiment set-up for rope elongation test

각각의 로프에 대하여 10 kg 하중이 가해졌을 때 신장률과 크리프 효과를 모델링 하기 위하여 180 sec 동안 하중을 가하 는 실험을 진행하였다. 이를 통해 로프의 모델링 파라미터들 을 추정하였다. 모델링 파라미터에 추정에는 Matlab의 System Ide.jpgication Toolbox를 사용하였으며 데이터의 수집 주기는 100 Hz이다. 추정된 모델 파라미터는 [Table 3]과 같다.

[Table 3]

Burgers model parameters of the climbing ropes

추정된 파라미터의 유효성은 실험 데이터와 시뮬레이션을 통한 추정 값과의 RMS 값을 통해 검증하였다. 이 때 사용된 RMS의 식은 아래와 같다. 이 식에서의 y_simulation은 시뮬레이 션 결과의 위치 값, y_measure은 실제 실험에서의 위치 값이며 단위는 m이다.

RMS의 값은 [Table 3]에 포함하였으며 100 N의 단위 계단 입력을 인가했을 때 모두 10^-3의 오차범위 이내에서 로프의 신장률을 구할 수 있었다.

실험 결과를 통해 같은 재질의 로프를 사용하더라도 심선 의 개수와 조합에 따라 같은 인장력에 대해서도 변형률이 크 게 달라질 수 있음을 확인하였다. 실험 데이터와 시뮬레이션 추정 값의 비교는 [Fig. 9]을 통하여 확인할 수 있다. 그래프를 통해 각 로프에 단위 계단 입력이 인가되면 초기에는 Kelvin- Voight 모델과 같이 병렬의 스프링 댐퍼와 같이 거동하며 진동 이 제거된 정상상태에 도달하더라도 크리프효과에 의해 로프 는 계속 인장 되는 것을 확인 할 수 있다(Maxwell 모델). 따라 서 등반 로프는 Burgers 모델을 이용하여 효과적으로 모델링 할 수 있으며 본 파라미터 값을 이용하면 ROPE RIDE의 위치 를 예측할 수 있을 것으로 기대된다.

[Fig. 9]

Elongation test of climbing ropes

5. 결 론

본 논문에서는 옥상에 고정된 등반 로프를 이용하여 등 하 강하는 ROPE RIDE의 위치를 정확하게 추정하기 위하여 로프 의 구성방정식을 구하고 다양한 종류의 로프의 파라미터들을 구하였다. 예비실험을 통하여 Kelvin-Voight 모델과 Maxwell 모 델을 혼합한 Burgers 모델로 로프를 모델링할 수 있음을 보였 으며 실험을 통하여 다양한 종류의 등반 로프에 대하여 모델 의 파라미터를 구하였다. 또한 모델의 파라미터를 이용한 시 뮬레이션 결과와 실제 실험 데이터와의 비교를 통해 본 모델 의 유효성을 검증하였으며 이를 통해 본 논문에서 제안하고 있는 등반 로프의 모델과 파라미터를 통해 실제 ROPE RIDE 의 위치를 예측 가능함을 확인할 수 있었다.

Acknowledgments

This research was supported by the National Research Foundation of Korea(NRF) Grant funded by the Ministry of Science and ICT for First-Mover Program for Accelerating Disruptive Technology Development (NRF-2018M3C1B9088328).

References

• T. Akinfiev, M. Armada, and S. Nabulsi, “Climbing cleaning robot for vertical surfaces,” Industrial Robot: An International Journal of Robotics Research and Application, vol. 36, no. 4, pp. 352-357, 2009. [https://doi.org/10.1108/01439910910957110]
• N. Elkmann, D. Kunst, T. Krueger, M. Lucke, T. Bohme, T. Felsch, and T. Sturze, “SIRIUSc – façade cleaning robot for a high-rise building in Munich, Germany,” Climbing and Walking Robots, pp.1033-1040, 2004. [https://doi.org/10.1007/3-540-29461-9_101]
• S.-M. Moon, J. Huh, D. Hong, S. Lee, and C.-S. Han, “Vertical motion control of building facade maintenance robot with built-in guide rail,” Robotics and Computer-Integrated Manufacturing, vol. 31, pp. 11-20, Feb., 2015. [https://doi.org/10.1016/j.rcim.2014.06.006]
• T. Kim, Y. Jeon, S. Yoo, K. Kim, H. S. Kim, and J. Kim, “Development of a wall-climbing platform with modularized wall-cleaning units,” Automation in Construction, vol. 83, pp.1-18, Nov., 2017. [https://doi.org/10.1016/j.autcon.2017.07.004]
• J. F. Flory, V. Ahjem, and S. J. Banfield, “A new method of testing for change-in-length properties of large fiber-rope deepwater mooring lines,” Offshore Technology Conference, Houston, Texas, USA, pp. 1087-1096, 2007. [https://doi.org/10.4043/18770-MS]
• C. Martins, V. Pinto, R. M. Guedes, and A. T. Marques, “Creep and stress relaxation behaviour of PLA-PCL fibres – A linear modelling approach,” Procedia Engineering, vol. 114, pp.768-775, 2015. [https://doi.org/10.1016/j.proeng.2015.08.024]
• A. Takata, G. Endo, K. Suzumori, H. Nabae, Y. Mizutani, and Y. Suzuki, “Modeling of Synthetic Fiber Ropes and Frequency Response of Long-Distance Cable-Pully System,” IEEE Robotics and Automation Letters, vol. 3, no. 3, pp. 1732-1750, Jul., 2018. [https://doi.org/10.1109/LRA.2018.2803204]
• W. N. Findley, J. S. Lai, and K. Onaran, “Linear Viscoelastic Constitutive Equations,” Creep and Relaxation of Nonlinear Viscoelastic Materials, Dover Publications, INC., New York, 1976, ch. 5, sec. 4, pp. 51-68.