안정적 로봇 파지를 위한 인공신경망

1. 서 론

로봇 매니퓰레이터는 산업현장 뿐만 아니라 자연 재해와 같은 극한 상황, 전쟁과 같은 위험한 분야, 미세한 작업이 필요 한 의료분야 등에서 인간을 대신한 작업수행을 대신한다.

매니퓰레이터를 통한 작업은 사용자가 미리 프로그래밍 한 경로와 움직임에 따라 같은 동작만을 반복하는 경우가 대부분 이었다. 그렇기에 매니퓰레이터의 작업은 갑작스럽게 변하는 환경이나 새로운 환경에 놓이게 되면 스스로 판단하여 행동을 수정하는 수준에 이르지 못하였다. 이러한 단점을 극복하고자 로봇 제어 프로그래밍을 매니퓰레이터 하드웨어에 국한되게 구성한 것을 넘어, 카메라 센서를 통한 비전인식, 촉각 센서를 이용한 그리퍼 제어 등 공학적인 방법을 융합 및 응용하기 시 작했다. 또한 매니퓰레이터와 robot hand의 제어 기술 개발은 단순 반복 작업만을 수행하던 과거와 달리, 인간의 작업에 활 용되는 도구를 그대로 사용하여 인간의 작업을 대체할 뿐만 아니라, 실생활에 도움 되는 여러 가지 다양한 서비스의 제공 을 가능하게 하는 이점이 있다.

로봇 매니퓰레이터와 인간의 손을 모방한 robot hand를 사 용하여 여러 종류의 다양한 물체들을 안정적으로 파지하는 연 구는 여전히 도전적인 주제이이고, 이러한 이점을 활용하기 위하여 필수적으로 선행개발 되어야 할 기술이다^[1,2].

본 논문에서는 3-Degree Of Freedom (DOF)로 구성된 3 finger robot hand를 이용하여 형태가 다양한 물체들을 파지하 고, 이송하는 작업을 연구한다. 제 1장 서론에 이어서 2장에서 robot arm의 시스템 구성에 대해 서술하고, 3장에서는 파지가 능한 물체의 유형을 10가지로 분류하고, 물체에 따른 파지 가 능한 후보점들 중에서 최적의 파지점을 5가지 목적함수를 통 하여 도출하고 각 가중치를 A.jpgicial Neural Network로 학습 하여 최적의 파지점을 도출하는 알고리즘에 대해 서술한다. 4 장에서는 도출된 최적의 안정 파지점을 실제 robot hand로 파 지 및 이송 실험에 적용하여 결과와 성능을 확인하고, 마지막 5장에서 결론을 통해 마무리한다.

2. Robot Arm의 시스템 구성

2.1 Robot Hand의 시스템 구성

Robot Hand는 파지 작업에 따라 여러 가지 형태가 존재하 고 이를 매니퓰레이터 끝단에 교체하여 사용된다.

본 실험에서는 일반적인 DC서보모터에 제어기가 삽입된 Dynamixel로 구성된 3-finger robot hand로 물체를 파지한다. 물체 의 형태, 무게, 재질의 다양성으로 인하여 대표적인 10가지 타입 을 정하고 이 대표물체들의 형상에 따라서 기하학에 기반한 최적 의 파지점과 자세를 도출하고 이를 neural network로 구현한다.

최적의 파지 작업을 위해서 먼저 파지가 가능한 최대 및 최 소 범위를 정해야 되고, 이는 robot hand의 하드웨어 스펙에 따 라 달라진다. 본 논문에서 사용된 robot hand의 구성은 [Fig. 1] 과 같다. Robot hand는 400 g 정도의 무게를 가지며, 파지 가능한 payroad는 약 1.5 kg이다.

[Fig. 1]

Robot Hand Hardware specification

2.3 Robot 매니퓰레이터의 시스템 구성

물체의 파지 실험에 사용된 6 자유도의 로봇 매니퓰레이터 의 구성은 [Fig. 2]와 같다. DC 모터 5개로 구성된 5자유도의 매니퓰레이터에 dynamixel (MX-64)를 추가하여 6 자유도를 구성한 뒤 끝단에 robot hand를 부착하였다.

[Fig. 2]

Robot Manipulator System configuration

3. SG-ANN

3.1 안정적 파지를 위한 A.jpgicial Neural Network

Stable Grasping A.jpgicial Neural Network (SG-ANN)는 [Fig. 3]과 같이 구성된다.

[Fig. 3]

SG-ANN block diagram

Robot hand로 파지 할 수 있는 물체의 최대 폭과 길이, 파지 가능 무게 등의 하드웨어 정보, 물체의 테두리 좌표정보(x, y, h)를 입력 받는다. 물체의 정보와 RGB-D 센서를 이용한 CNN 처리를 통해 파지 대상물체를 10가지 타입의 원형으로 분류하 고^[3,4], 각각의 물체 형태에 대하여 파지점들의 위치로 이루어 진 파지 후보 군을 물체와 robot hand의 특성을 고려하여 파지 가능한 최적의 높이와 폭, 물체의 중심점을 고려한 정규분포의 확률 밀도 함수를 구성하여 가치함수에 적용하고^[5-8], 도출된 각 목적함수의 가중치를 물체별로 Neural network를 통해 학습시 켜 각 물체 별 최적의 파지점에 대한 가중치를 도출하여 안정적 인 파지작업을 수행한다^[9-12]. 도출된 파지점을 robot hand의 핑 거길이를 고려한 파지가능 깊이를 고려하여 6 cm이내의 경우 물체의 윗면에서 파지하고, 7 cm를 초과하는 경우 옆면에서 파 지하도록 한다. robot hand의 제어에는 PID 제어기가 사용된다.

3.2 Geometry 기반의 목적 함수 구성

정규분포의 확률 밀도함수를 통해 안정적 파지를 위한 objective function 도출하는데 아래의 5가지의 판단기준이 사 용된다.

1. 물체의 형태에 따른 안정된 파지 점의 높이 평균
2. 파지 점의 높이 차이
3. 최적의 파지 폭
4. 물체 기하학적 중심의 최적 위치
5. 물체의 무게 중심의 최적 위치

5가지의 판단기준들은 최적의 평균 값을 기준으로 양쪽으 로 cost가 점점 감소하는 확률 밀도 함수를 objective function으 로 활용하여 [Fig. 4]와 같이 구성된다. 각 조건들의 최대, 최솟 값을 이용하여 표준편차를 구하여 이용한다. 이 방법을 통하 여 최적의 값이 가장 높은 cost를 얻을 수 있으며, 그 또한 근처 값을 중심으로 높은 cost를 얻는다.

[Fig. 4]

Objective function of neural network

$\[ f\left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{\left(x-\mu \right)}^2}{2\sigma }} \]$

(1)

$\[ Z=\frac{\left(a\hspace{0.33em}\text{or}\hspace{0.33em}b\right)-\kappa }{\sigma } \]$

(2)

σ는 표준편차이며, 확률 변수 Z에 의해 결정되며 관계식은 식 (2)와 같다. 식 (1)에서 x는 각 가치 함수에 입력으로 들어가 게 될 변수이며, x의 최대값을 a, 최소값을 b라고 정의한다. 확 률변수는 각 가치 함수에 맞게 정하여 함수를 구성하였다.

대부분의 가치가 최소값과 최대값 사이에 나오도록 확률 변수를 설정하였다. κ는 확률 밀도 함수에서 평균 값을 뜻하 며, 함수가 평균 값을 기준으로 대칭을 이룸과 동시에 평균 값 에서 최고의 가치가 도출되도록 설정한다. 본 논문에서는 각 가치 함수에 사용되는 평균 값을 최적의 값으로 설정하였다.

또한 함수에서 사용하는 임의의 파지 점 두 개는 아래 [Fig. 5] 와 식 (3)에서 보이듯이 p₁, p₂로 표현한다.

$\[ \begin{array}{l}{P}_1=\left[P_{1,x},\hspace{0.33em}{P}_{1,y},\hspace{0.33em}{P}_{1,h}\right]\\ P_2=\left[P_{2,x},\hspace{0.33em}{P}_{2,y},\hspace{0.33em}{P}_{2,h}\right]\end{array} \]$

(3)

[Fig. 5]

Center of shape & grasping point

3.2.1 파지 높이에 대한 목적 함수

물체를 안정적으로 파지하기 위해서는 두 파지점의 높이가 비슷하여야 한다. 높이와 관련된 목적 함수를 구성하기 위해 물체가 파지 가능한 최대의 높이 h를 먼저 구한다, 또한 확률 변수 Z는 3으로 설정하여 최댓값과 최솟값 사이의 가치가 99%로 나오게 설정하였다.

높이와 관련된 목적 함수는 총 두 가지 경우로 분류한다. 임 의로 선택된 파지점 두 개의 높이 평균과 높이 차이를 이용한 다. 높이의 평균이 최적의 높이일 때, 두 파지점의 높이의 차가 최소일 때 안정적인 파지가 가능하며, 가장 높은 가치를 가지 게 된다.

먼저, 높이의 평균을 통한 목적 함수의 구성이다.

$\[ h_{a\upsilon r}=\frac{h_1+h_2}{2} \]$

(4)

위 식을 이용하여 두 파지점의 평균(h_aυr)을 알아낸다. 식 (4)에서 h₁은 파지 점 P₁에서의 h축 좌표 값이며, h₂는 P₂에서 의 h축 좌표 값이다. 두 파지점의 평균을 이용하여 다음 확률 밀도 함수 식 (5)에 대입하여 가치를 구한다. 높이 최적 값(κ) 은 미리 정해 높은 10가지의 물체 형태를 가장 안정적으로 파 지하는 높이로써, 파지 작업 실험을 통해 알아내어 사용하였 다. 표준 편차는 물체를 파지 가능한 최대값을 물체의 최대 높 이라고 설정하여, 미리 정한 확률변수와 식 (2)를 이용하여 구 하였다.

다음으로, 파지점의 높이의 차이를 최소로 하는 목적 함수 의 구성이다. 파지 할 때 robot hand의 두 파지점이 비슷한 높이 에서 파지 하는 것이 안정적으로 파지 가능하다. 따라서 두 파 지점의 높이의 차이를 절대값이 작을수록 안정적인 값으로 설 정한다.

$\[ h=h_1-h_2 \]$

(5)

위 식을 통하여 두 파지점의 높이 차이를 구한다. h₁은 파지 점 P₁에서의 h축 좌표 값이며, h₂는 P₂에서의 h축 좌표 값이다.

$\[ f_H\left(h\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{h^2}{2{\sigma }^2}} \]$

(6)

확률 밀도 함수 식(6)에 대입하여 파지점의 높이 차에 대한 가치를 구한다. 최적 값은 두 높이의 차이가 -(최대 높이) ~ + (최대 높이)이므로 0으로 설정하여 적용하였다. 표준 편차(σ) 는 최대값을 물체의 최대 높이라고 설정하며, 미리 정한 확률 변수와 식 (2)를 이용하여 구하였다.

3.2.2 파지 폭에 대한 목적 함수

물체를 집을 수 있는 폭을 robot hand의 특성에 맞추어 최적 파지 폭을 정하게 된다. 본 실험에서 사용된 3-DOF robot hand 는 2 cm ~ 15 cm 사이의 폭으로 파지하는 것이 가능하며, 그 중 심 폭인 8.5 cm 로 파지되는 것을 최적의 폭으로 설정하였다. 확률변수는 약 1.92로 설정하여 5 cm ~ 11 cm 사이에 cost가 90%가 나오게 정하였다. 폭의 경우 최소나 최대 파지 점에서 도 파지가 불가능하지 않기에 확률 변수를 높게 설정하지 않 았다.

$\[ f_W=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{{\left(w-8.5\right)}^2}{2{\sigma }^2}} \]$

(7)

$\[ w=\sqrt{{\left(P_{1,x}-P_{2,x}\right)}^2+{\left(P_{1,y}-P_{2,y}\right)}^2+{\left(P_{1,z}-P_{2,z}\right)}^2} \]$

(8)

위의 확률 밀도 함수 식 (7)에 대입하여 최종 가치를 구한다. 표준 편차(σ)는 최대값을 파지 안정적인 최대 폭(11 cm)라고 설정하여, 앞서 정한 확률변수와 식 (2)를 이용하여 구하였다.

3.2.3 물체의 기하학적 중심에 대한 목적 함수

물체를 파지 시에 물체의 기하학적 중심점에 가까운 곳을 파지하는 방법이 가장 안정적이기에 목적 함수를 설정한다. 파지 지점 P와 물체 중심 s와의 각도 차이가 작을수록 중심과 일직선에 가까우며 안정적인 파지가 가능하다. 이 각도의 차 이를 통하여 최적의 파지 위치를 판별한다. (x, y), (x, h), (y, h) 평면 s 에서 각각의 각도 차 s_a,b를 합산하여 적용한다. μ = 0 이고, 확률변수를 3으로 적용하여 cost를 구한다.

$\[ {\theta }_{s_1\left(\alpha ,\beta \right)}=\text{arctan}\hspace{0.33em}(\frac{P_{1,\beta }-{\beta }_s}{P_{1,\alpha }-\alpha {}_s}) \]$

(9)

$\[ {\theta }_{s_2\left(\alpha ,\beta \right)}=\text{arctan}\hspace{0.33em}(\frac{P_{2,\beta }-{\beta }_s}{P_{2,\alpha }-\alpha {}_s}) \]$

(10)

여기서 $$ \left(\alpha ,\hspace{0.33em}\beta \right)∍\left\{\left(x,y\right),\hspace{0.33em}\left(x,h\right),\hspace{0.33em}\left(y,h\right)\right\}$$ 이다.

각 평면에 관한 각도 차이(s)를 구하면 다음과 같다.

$\[ \begin{array}{l}{f}_s\left(s\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{s^2}{2{\sigma }^2}}\\ s_{x,y}=\left({\theta }_{s_1\left(x,y\right)}-{\theta }_{s_2\left(x,y\right)}\right)\\ s_{x,h}=\left({\theta }_{s_1\left(x,h\right)}-{\theta }_{s_2\left(x,h\right)}\right)\\ s_{y,h}=\left({\theta }_{s_1\left(x,h\right)}-{\theta }_{s_2\left(x,h\right)}\right)\\ s=s_{x,y}+s_{x,h}+s_{y,h}\end{array} \]$

(11)

다음과 같이 구한 각도 차이를 확률밀도함수를 이용하여 cost를 구한다. 표준 편차(σ)는 최대값을 90°라고 설정하여, 미 리 정한 확률 변수와 식 (2)를 이용하여 구한다.

3.2.4 물체의 무게 중심에 대한 목적 함수

물체를 파지 하였을 때 중력에 의하여 물체의 회전이 발생 하는 경우가 있다. 이를 피하기 위해, 물체의 무게에 따른 중심 점을 고려하여 회전각이 최소가 되는 파지점을 판단한다. 즉, robot hand로 물체를 잡았을 때 두 파지점의 연결선 상에 물체 의 무게 중심점이 포함되면 안정적인 파지가 가능하다. 최적 의 파지 위치 계산은 기하학적 중심 목적 함수에서 구한 방법 과 유사하다.

$\[ {\theta }_{m_1\left(\alpha ,\hspace{0.33em}\beta \right)}=\text{arctan}\hspace{0.33em}\text{(}\frac{P_{1,\beta }-{\beta }_m}{P_{1,\hspace{0.33em}\alpha }-{\alpha }_m}\text{)} \]$

(12)

$\[ {\theta }_{m_2\left(\alpha ,\hspace{0.33em}\beta \right)}=\text{arctan}\hspace{0.33em}\text{(}\frac{P_{2,\beta }-{\beta }_m}{P_{2,\hspace{0.33em}\alpha }-{\alpha }_m}\text{)} \]$

(13)

여기서 $$ \left(\alpha ,\hspace{0.33em}\beta \right)∍\left\{\left(x,y\right),\hspace{0.33em}\left(x,h\right),\hspace{0.33em}\left(y,h\right)\right\}$$ 이다. 위 식을 이용하 여 무게 중심점을 기준으로 각 파지점의 각도 차이(m)을 구한다.

$\[ \begin{array}{l}{f}_M\left(m\right)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{m^2}{2{\sigma }^2}}\\ m_{x,y}=\left({\theta }_{m_1\left(x,y\right)}-{\theta }_{m_2\left(x,y\right)}\right)\\ m_{x,h}=\left({\theta }_{m_1\left(x,h\right)}-{\theta }_{m_2\left(x,h\right)}\right)\\ s_{y,h}=\left({\theta }_{m_1\left(y,h\right)}-{\theta }_{m_2\left(y,h\right)}\right)\\ m=m_{x,y}+m_{x,h}+m_{y,h}\end{array} \]$

(14)

각 평면 각도의 차이를 구한 뒤 합산하여 목적 함수에 이용 할 변수를 구한다. 표준 편차(σ)는 기하학적 중심 가치 함수와 마찬가지로 최대값을 90°, 확률 변수를 3으로 설정하여, 식 (2) 를 이용하여 구한다.

3.2.5 안정 파지 점의 최종 목적 함수

앞에서 구한 가치들을 목적 함수의 최댓값으로 나누어 가 치의 범위를 0 ~ 1사이로 비례하게 변환한다. 식 (15)와 같이 구한 높이의 가치, 폭의 가치, 기하학적 중심의 가치, 무게 중 심의 가치들을 합산하여 물체별로 가치가 최대가 나오게 되는 파지점의 좌표를 도출하게 된다. 가치의 최댓값을 도출하는 방법으로 machine learning의 한 기법인 maximize을 사용하여 최적의 파지 점을 구하게 된다. Maximize는 변화되는 입력 변 수에 따라 cost의 변화율을 판단하여, 가치가 더 나은 입력 변 수를 찾아내어 최적의 파지점을 구하게 된다.

$\[ \begin{array}{c}Cost\left(x\right)=w_1\frac{f_H\left(h\right)}{f_H\left({\kappa }_h\right)}+w_2\frac{f_{H_{a\upsilon r}}\left(h_{a\upsilon r}\right)}{f_{H_{a\upsilon r}}\left({\kappa }_{h_{a\upsilon r}}\right)}+w_3\frac{f_W\left(w\right)}{f_W\left({\kappa }_w\right)}\\ +w_4\frac{f_s\left(s\right)}{f_s\left({\kappa }_s\right)}+w_5\frac{f_M\left(m\right)}{f_M\left({\kappa }_m\right)}\end{array} \]$

(15)

여기서 도출된 최적 파지점에서 w_i의 값은 neural network 의 모델 중 다층 퍼셉트론(Multi-layer Perceptron)을 사용하여 학습하였다. [Fig. 6]은 뉴럴 네트워크의 구조를 나타낸 것으로 각 목적함수를 통해 도출된 5개의 파지요소를 순차적으로 1000번 입력하여 5000개의 파지 목적함수를 입력으로 하고, 각 물체별로 목적함수의 가중치 중 안정된 파지작업의 최적값 을 도출한다.

[Fig. 6]

Structure of Neural Network

Neural network의 구조는 아래와 같다.

Network type : Feed-forward back propagation

Performance (cost) function : SGD(Stochastic Gradient Descent) Training function : Sigmoid, ReLU

경사하강법(gradient decent method)과 역전파(back propagation) 의 적용으로 각 물체 당 각 코스트별 최적의 result(W)값을 도 출하여 최적 파지점을 구한다. 여기서, neural network은 최적 weight 값의 도출을 위한 학습에 쓰이고, 학습 된 데이터를 적 용하여 파지 실험을 진행하였다.

$\[ Result\left(W\right)=Y_{op}-H\left(X\right) \]$

(16)

$\[ H\left(X\right)=\text{cos}t={\displaystyle \sum _{i=1}^5{w}_i\text{cos}{t}_i} \]$

(17)

$\[ Y_{op}=w_1\hspace{0.33em}·\hspace{0.33em}1+w_2\hspace{0.33em}·\hspace{0.33em}1\hspace{0.33em}+w_3\hspace{0.33em}·\hspace{0.33em}1+w_4\hspace{0.33em}·\hspace{0.33em}1+w_5\hspace{0.33em}·\hspace{0.33em}1 \]$

(18)

$\[ W:=W-\frac{d}{dW}Result\left(W\right) \]$

(19)

입력과 w에 따른 결과 변화율을 예측함으로써 효율적인 w 값을 도출한다.

3.3 물체의 분류

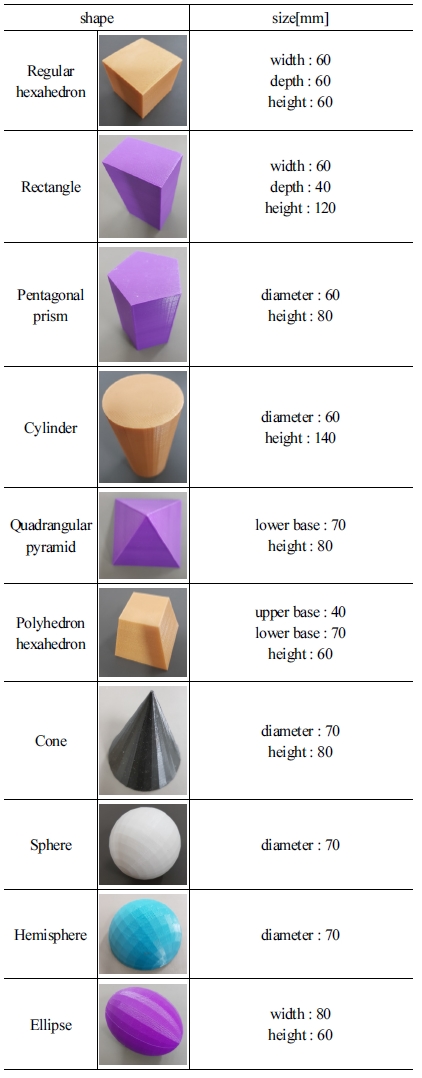
RGB-D 센서를 통해 물체를 인식 한 후 CNN 처리를 통해 물체의 파지가능한 후보군을 생성하고, 센서를 통해 인식된 물 체를 분류하기 위해 machine learning에서 대표적으로 사용하 는 classification algorithm인 supervised learning을 이용한다. supervised learning은 데이터에 대한 label이 주어진 상태에서 컴 퓨터를 학습시키는 방법이다. 본 실험에는 [Table 1]과 같이 크게 10가지의 형태와 크기의 label 데이터를 사용하여 학습한다^[3,4].

[Table 1]

10 types of grasped objects

3.4 시뮬레이션 구성 및 학습

시뮬레이션은 파지 대상 물체를 일반화 시킨 10가지의 형 태의 물체와 좌표들로 진행한다. 미리 정해 놓은 10가지 물체 중 rectangle, cylinder, quadrangular pyramid, cone 타입으로 각 각 나누고, 3D 파일로 시뮬레이터에 삽입한다. 각 물체는 다음 그림에서 나타나는 확률밀도함수를 사용하여 약 5,000개의 샘플을 가지고 최적의 파지점을 도출하였다. [Fig. 7] ~ [Fig. 10] 는 각 물체의 높이(차이, 평균)에 따른 확률 밀도 함수로 나타 낸 것이다. 왼쪽의 그래프는 높이 차이에 대한 목적 함수로써 인식된 물체의 파지점간의 높이 차이로 -(최대 높이) ~ ＋(최 대 높이)의 사이에 가치들이 표현되고, 0에서 최대값을 가진 다. 오른쪽의 그래프는 파지 높이의 평균에 대한 목적함수로 써 직육면체, 원기둥, 정사각뿔, 원뿔의 최적의 파지 높이인 6 cm, 7 cm, 2 cm, 4 cm와 같다. [Fig. 11]은 폭과 기하학적 중심 및 무게 중심과 관련된 확률 밀도 함수이다. 기하학적 중심과 무게 중심 확률 밀도 함수는 구하는 방식이 동일하고, 최소값, 최대값, 최적값이 같기 때문에 가치 함수 그래프는 동일하다.Fig. 8, 9

[Fig. 7]

Optimal grasp height graph of rectangle

[Fig. 8]

Optimal grasp height graph of cylinder

[Fig. 9]

Optimal grasp height graph of quadrangular pyramid

[Fig. 10]

Optimal grasp height graph of cone

[Fig. 11]

Optimal grasp width and center of shape&mass graph

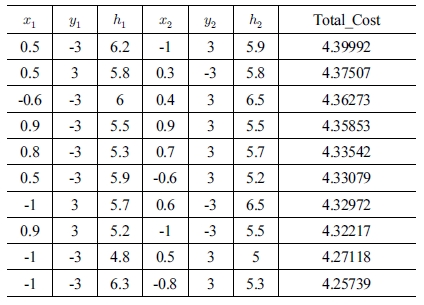
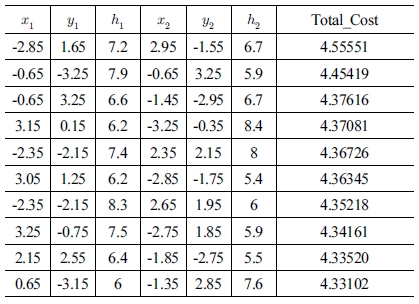
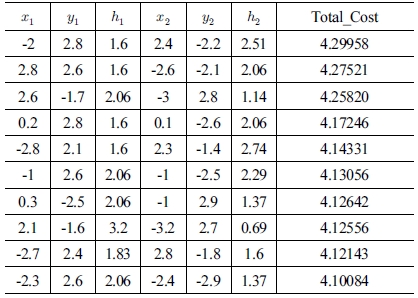
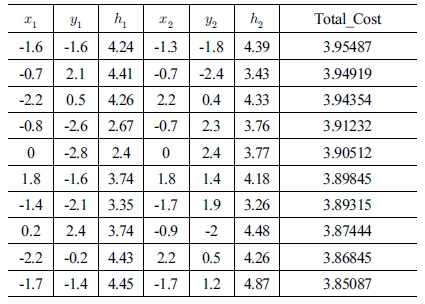
[Table 2] ~ [Table 5]는 각 물체의 밑면에서의 중심점을 (0, 0, 0)으로 기준으로 두 파지점의 위치 좌표를 각 목적 함수에 적용하여, Cost가 높은 상위 10개의 파지점을 나타내었다. Table 3, 4

[Table 2]

Top 10 coordinate pairs of rectangle

[Table 3]

Top 10 coordinate pairs of cylinder

[Table 4]

Top 10 coordinate pairs of quadrangular pyramid

[Table 5]

Top 10 coordinate pairs of quadrangular cone

4. 실 험

시뮬레이션을 통해 도출된 파지 후보군 중 최적 파지 위치 를 이용하여 robot hand로 개별 물체를 파지한다. 파지 대상 물 체는 시뮬레이션 된 대상 물체 중에서 rectangle, cylinder, quadrangular pyramid, cone의 4가지 물체로 정하고, 도출된 최 적 파지 위치에 따라서 robot hand로 실제 제작된 물체를 파지 한다^[13,14].

파지 실험은 robot hand가 물체를 파지하고 물체가 놓인 위 치로부터 20 cm 위로 들어 올린 뒤, 5초 동안 물체를 놓치지 않 고 파지 상태를 유지하는 것을 성공이라 보고, 물체 당 20번씩 파지 실험을 진행하였다.

[Fig. 12] ~ [Fig. 15]에 나타난 붉은 색의 선들은 학습을 통해 도출된 파지 위치 점들 중에서 Total_Cost가 높은 상위 10개의 쌍을 표시한 것이고, 초록 색의 선은 가장 높은 Total_Cost를 지닌 안정적인 파지점을 의미한다. Fig. 13, 14

[Fig. 12]

Retention candidate and operation of rectangle

[Fig. 13]

Retention candidate and operation of quadrangular pyramid

[Fig. 14]

Retention candidate and operation of cylinder

[Fig. 15]

Retention candidate and operation of cone

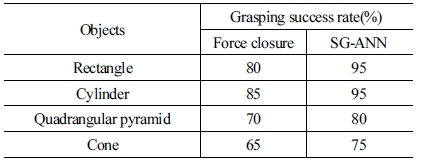
제안한 알고리즘의 우수성을 입증하기 위하여 두 가지 실 험 방법으로 파지 성공률을 측정 후 비교한다. SG-ANN을 통 하여 최적 파지 점을 도출하고, 이를 통해 파지한 SG-ANN의 방법과 RGB-D 센서를 통해 물체를 인식하고 CNN을 통해 파 지위치를 도출하고, 이 위치점을 이용하여 물체 별로 무게 중 심과 평행하게 무게 힘에 해당하는 힘으로 파지하도록 한 Force- closure 방법을 비교 하였고^[15], 각 물체별로 파지 실험 시 파지 성공률을 [Table 6]에 나타내었다. 최적 파지 점을 적 용한 SG-ANN의 경우 직사각형과 원통형 물체를 파지 시에 각각 19번의 높은 파지 성공률을 보였다. Force-closure를 사용 하여 물체의 무게 중심만을 고려한 경우, 일정 높이에서 물체 의 파지상태를 유지하지 못하고 물체가 많이 미끄러지는 현상 이 나타났고 SG-ANN의 최적파지 점 도출을 통해 이를 극복 하였다. 또한 사각뿔과 원뿔처럼 파지하기 힘든 물체의 경우 에도 SG-ANN에서 높은 파지 성공률을 달성하였다.

[Table 6]

Comparison of grasping success rate

5. 결 론

3 자유도의 로봇핸드를 통한 물체의 안정적인 파지 작업을 수행하기 위하여, 파지 대상 물체를 정하고, 파지 대상 물체의 형태와 robot hand의 특성과, 파지 가능한 최적의 높이와 폭, 물체의 중심점 등의 기하학적인 정보를 이용하여 목적함수에 적 용하고 neural network를 구성하여 최적의 파지 위치를 도출한다.

다양한 물체를 10가지 대표형태로 분류하고, 실제 물품과 대표되는 형태로 제작된 물체들을 각각 robot hand를 통한 실 제 파지 작업을 수행하였고, 제안한 알고리즘과 기존에 사용 되는 방법을 비교하여 테스트하였다. 추후 robot hand의 파지 힘 벡터가 friction cone 내부에 존재하도록 neural network의 parameter를 피드백 제어하여 auto tuning하는 방법에 대하여 연구 할 예정이다.

References

• Z. Li and S. Sasty, “Task-Oriented Optimal Grasping by Mu.jpgingered Robot Hands,” 1987 IEEE International Conference on Robotics and Automation, Raleigh, NC, USA, 1988, DOI: 10.1109/ROBOT.1987.1087852. [https://doi.org/10.1109/ROBOT.1987.1087852]
• N. Daoud, J.P. Gazeau, S. Zeghloul, and M. Arsicault, “A real-time strategy for dexterous manipulation: Fingertips motion planning, force sensing and grasp stability,” Robotics and Autonomous Systems, vol. 60, no. 3, pp. 377-386, 2011. [https://doi.org/10.1016/j.robot.2011.07.011]
• F. Ikhwantri, N. Habibie, A. R. Syulistyo, Aprinaldi, and W. Jatmiko, “Learning Semantic Segmentation Score in Weakly Supervised Convolutional Neural Network,” 2015 International Conference on Computers, Communications, and Systems (ICCCS), Kanyakumari, India, 2016, DOI: 10.1109/CCOMS.201 5.7562845. [https://doi.org/10.1109/CCOMS.2015.7562845]
• D. Rao, Q. V. Le, T. Phoka, M. Quigley, A. Sudsang, and A. Y. Ng, “Grasping Novel Objects with Depth Segmentation,” 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 2010, DOI: 10.1109/IROS.2010.5650493. [https://doi.org/10.1109/IROS.2010.5650493]
• D. Guo, F. Sun, B. Fang, C. Yang, and N. Xi, “Robotic grasping using visual and tactile sensing,” Information Sciences, vol. 417, pp. 274-286, Nov., 2017. [https://doi.org/10.1016/j.ins.2017.07.017]
• K.-W. Lim, S.-H. Kim, K.-B. Sim, and H.-T. Jeon, “Force Controller of the Robot Gripper using Fuzzy-Neural Fusion,” The Institute, Electronics and Information Engineers, pp. 861-865, 1991.
• B.-H. Kim, B.-J. Yi, S.-R. Oh, and I. H. Suh, “Optimal Grasp Planning of Object Based on Weighted Composite Grasp Index,” Journal of Control, Automation, and Systems Engineering, vol. 6, no. 11, pp. 1003-1012, 2000.
• P.-C. Huang, J Lehman, A. K. Mok, R. miikkulainen, and L. Sentis, “Grasping Novel Objects with a Dexterous Robotic Hand through Neuroevolution,” 2014 IEEE Symposium on Computational Intelligence in Control and Automation (CICA), Orlando, FL, USA, 2014, DOI: 10.1109/CICA.2014.7013242. [https://doi.org/10.1109/CICA.2014.7013242]
• M. R. CUTKOSKY, “On Grasp Choice, Grasp Models, and the Design of Hands for Manufacturing Tasks,” IEEE Transactions on Robotics and Automation, vol. 5, no. 3. pp. 269-279, Jun., 1989 [https://doi.org/10.1109/70.34763]
• T. Yoshikawa, “Mu.jpgingered robot hands: Control for grasping and manipulation,” Annual Reviews in Control, vol. 34, no. 2, pp. 199-208, Dec., 2010. [https://doi.org/10.1016/j.arcontrol.2010.09.001]
• M. Li, K. Hang, D. Kragic, and A. Billard, “Dexterous grasping under shape uncertainty,” Robotics and Autonomous Systems, vol. 75, Part B, pp. 352-364, Jan., 2016. [https://doi.org/10.1016/j.robot.2015.09.008]
• J. Mahler, F. T. Pokorny, B. Hou, M. Roderick, M. Laskey, M. Aubry, K. Kohlhoff, T. Kroger, J. Kuffner, and K. Goldberg, “Dex-Net 1.0: A Cloud-Based Network of 3D Objects for Robust Grasp Planning Using a Multi-Armed Bandit Model with Correlated Rewards,” 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 2016, DOI: 10.1109/ICRA.2016.7487342. [https://doi.org/10.1109/ICRA.2016.7487342]
• M.-Y. Park, J.-S. Yang, Y.-M. Koo, B.-K. Shim, Y.-K. Jeong, E.-U. Kang, and S.-H. Han, “A Study on Gripping Control of Robotic Hand with Ten Joints for Cooperative Working,” 2014 14th International Conference on Control, Automation and Systems (ICCAS 2014), Seoul, South Korea, 2014, DOI: 10.1109/ICCAS.2014.6988009. [https://doi.org/10.1109/ICCAS.2014.6988009]
• D.-J. Park, D.-E. Kim, J.-H. Park, and J.-M. Lee, “Singularity and Collision Avoidance Path Planning based upon A.jpgicial Potencial Field and Manipulability Measure,” Journal of The Institute of Electronics and Information Engineers, vol. 55, no. 5, pp. 89-96, May, 2018. [https://doi.org/10.5573/ieie.2018.55.5.89]
• H. Wakamatsu, S. Hirai, and K. Iwata, “Static Analysis of Deformable Object Grasping Based on Bounded Force Closure,” IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 1996, DOI: 10.1109/ROBOT.1996.509 219.