야지 주행 로봇을 위한 횡 방향 힘 추정 모델의 설계 및 마찰계수 추정 신뢰도의 향상
© Korea Robotics Society. All rights reserved.
Abstract
For a mobile robot that travels along a terrain consisting of various geology, information on tire force and friction coefficient between ground and wheel is an important factor. In order to estimate the lateral force between ground and wheel, a lot of information about the model and the surrounding environment of the vehicle is required in conventional method. Therefore, in this paper, we are going to estimate lateral force through simple model (Minimal Argument Lateral Slip Curve, MALSC) using only minimum data with high estimation accuracy and to improve estimation reliability of the friction coefficient by using the estimated lateral force data. Simulation is carried out to analyze the correlation between the longitudinal and transverse friction coefficients and slip angles to design the simplified lateral force estimation model by analysing simulation data and to apply it to the actual field environment. In order to verify the validity of the equation, estimation results are compared with the conventional method through simulation. Also, the results of the lateral force and friction coefficient estimation are compared from both the conventional method and the proposed model through the actual robot running experiments.
Keywords:
Rough Terrain, Soil, Mobile Robot, Lateral Force, Friction Model, Pacejka Model, Friction Coefficient1. 서 론
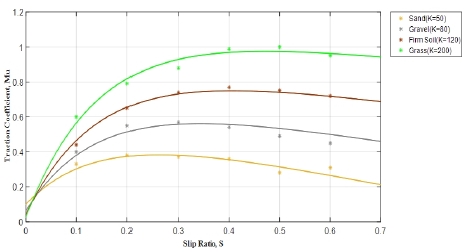
최근 정보통신기술(ICT)의 융합으로 이루어진 4차 산업혁명 이 대두되면서 국내뿐만 아니라 세계 각국에서 자율주행차량 에 대한 연구개발 및 상용화 기술개발이 활발하게 이루어지고 있다. 또한 우주와 같은 미지의 지역 탐사를 위한 다양한 탐사 로봇 개발연구도 꾸준히 진행되어지고 있다. 이러한 모바일 로봇들을 이용하여 위치추정, 경로계획, 매핑 등의 여러 연구 가 진행될 수 있다. 이를 위해서는 현재 주행환경에 대한 정보 와 환경 내 로봇 간의 상호작용에 대한 분석이 필수적이다. 따 라서 기존의 연구에서는 차량의 동역학적, 기구학적 모델의 분석과 실험을 통해 지면과 차량의 바퀴사이에서 발생하는 힘 에 대한 분석과 주행환경에 대한 정보를 획득하기 위해 각각 의 지질에 해당하는 마찰계수를 추정함으로써 주행환경의 지 질의 종류를 분류하는 연구가 진행되었다[1,2]. 선행연구에서 는 [Fig. 1]과 같이 모래, 자갈, 흙, 초목 등의 다양한 지질환경 에서 각각의 마찰계수를 추정함에 따라 지질의 종류를 분류할 수 있었다[3,4]. 그러나 실제 로봇이 주행하는 환경에서는 다양 한 변수가 존재하고 또한 로봇의 모델 역시 달라질 수 있기 때 문에 마찰계수 추정의 정밀도가 낮아지게 된다. 이러한 문제를 해결하기 위해 로봇 모델의 영향을 최대한 받지 않고 마찰계수 를 정밀하게 추정할 수 있도록 추정에 필요요소인 바퀴와 지면 사이에서의 종·횡 방향의 힘을 정밀히 추정해야 할 필요가 있다[5].
선행연구에서 차량 모델의 기구학적, 동역학적 분석을 통 해 지면과 바퀴 사이에서 발생하는 종 방향 힘과 슬립율, 슬립 각에 대한 추정이 정밀히 이루어졌지만 횡 방향 힘에 대해서 는 오차가 발생하는 것을 확인하였다. 바퀴에서의 횡 방향 힘 을 추정하기 위한 다른 대표적인 방법으로는 Pacejka Brush Model에 의한 추정법이 있다[6,7].
| (1) |
식 (1)은 Pacejka Brush Model로 이를 이용할 경우 정밀하게 횡 방향 힘을 추정할 수 있어 차량 시뮬레이터에서도 널리 사 용되는 방식이지만 수식을 사용하기에 있어 많은 인자들이 필 요함을 알 수 있다. 따라서 실시간으로 주행하는 차량에서 이 러한 많은 인자를 각각의 차량 모델에 맞도록 설정하고 힘을 추정하기에는 어려움이 있다. 또한 가상 환경과 달리 실제로 로봇이 주행하는 과정에서 지면의 마찰계수를 정확히 알 수 없기 때문에 추정한 힘의 결과도 그 신뢰도가 떨어지게 된다.
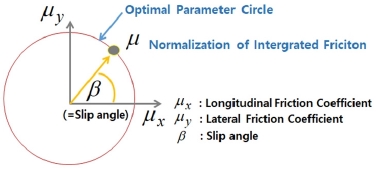
횡 방향 힘을 간단히 추정하기 위한 방법으로는 [Fig. 2]와 같이 종·횡 방향 힘의 벡터관계를 원으로 보는 Friction Circle 으로 가정하여 구하는 방법이 있다[8,9]. 그러나 Slip Angle의 범 위에 따라서 정밀한 추정이 불가능한 영역이 있으므로 이 부 분에 대한 문제해결이 필요하다. 따라서 본 논문에서는 다음 의 목적을 가지고 연구가 진행되었다.
- 1) 지면과 바퀴 사이의 횡 방향 힘을 추정하기 위해 사전에 기 존의 추정방식과 같이 미리 실험을 통해 얻어야 하는 많은 인자 대신에 실시간 주행을 통해 매 상황에 부합하는 추정 결과들만을 횡 방향 힘 추정 수식의 인자로 사용하여 기존 의 연구보다 간략하며 유사한 추정결과를 얻을 수 있는 마 찰 모델 수식을 설계한다.
- 2) 횡 방향 힘을 추정하여 각 바퀴에서의 마찰계수 추정 결과 의 분산을 줄여 추정 결과의 신뢰도를 높이고 마찰계수 추 정 정밀도를 향상시킨다.
본 논문에서는 이러한 목적을 충족시킬 수 있도록 마찰 모 델 수식 설계 및 마찰계수 추정 정밀도를 향상시키기 위해 차 량 시뮬레이터를 이용하여 분석하고 지질 분석 실험 장치와 실외 야지환경에서의 로봇 주행 실험을 통해 검증하였다.
2. 횡 방향 힘 추정을 위한 모델 설계
2.1 횡 방향 힘 추정 모델 설계 개요 및 시뮬레이션 환경
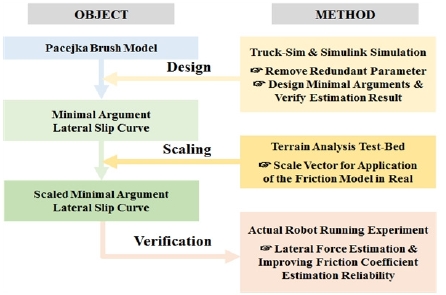
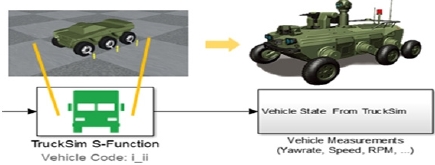
본 논문에서는 [Fig. 3]에 따라 을 추정하기 위한 연구를 진행하였다. 기존의 추정 방식을 이용하여 실시간으로 을 추정하기에 어려움을 주는 인자들을 사용하지 않고 을 추 정하기 위한 모델을 설계하기 위해 먼저 [Fig. 4]의 차량에 대 한 가상 시뮬레이션 플랫폼인 Truck-sim과 Matlab의 Simulink 의 Co-Simulation을 통해 진행하였다. 시뮬레이션에서 사용한 차량모델은 국방과학연구소의 견마로봇을 모델로 사용하였 다[9]. 가상 시뮬레이션은 평탄한 지면에 모래, 자갈, 흙, 초목을 대표하는 마찰계수인 0.4, 0.6, 0.75, 0.9의 4가지 마찰계수에서 슬립각의 범위가 넓게 나타나는 나선형의 주행을 진행하였다. 연구는 먼저 시뮬레이션을 통해 기본적 함수 형태에 대해 분 석하고 이에 따라 실시간으로 사용하기 어려운 인자들을 제외 하고 최소한의 인자들을 이용한 모델을 설계한다. 이후 가상 환경이 아닌 실제 환경에 모델을 적용하기 위한 스케일링실험 을 지형 분석 장치를 이용하여 진행한다. 마지막으로 주행로 봇을 이용한 실제 환경에서의 실험에서 설계한 모델을 통한 횡 방향 힘의 추정 및 마찰계수 추정 신뢰도 향상에 대한 검증 을 진행한다. 이후 시뮬레이션과 실험에서 사용하는 기호는 아래와 같이 정의하였다.
- ∙Fx : Wheel's Longitudinal Force (N, ≠ wton)
- ∙Fy : Wheel's Lateral Force (N, ≠ wton)
- ∙Fz : Wheel's Vertical Force (N, ≠ wton)
- ∙μx : Longitudinal Friction Coefficient
- ∙μy : Lateral Friction Coefficient
- ∙Sa : Slip Angel (°, degree)
2.2 횡 마찰 곡선 모델 설계
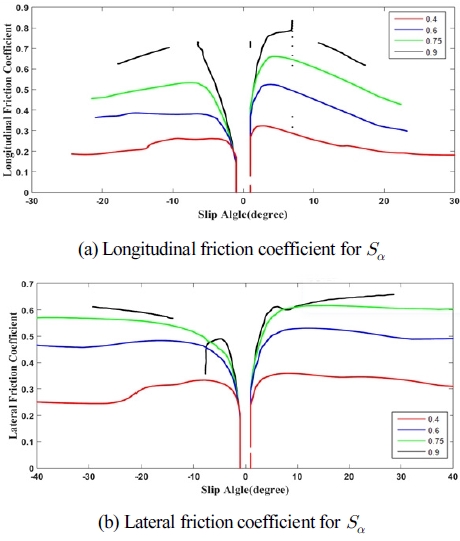
바퀴에서 발생하는 힘은 마찰에 의한 미끄러짐이 존재할 때 발생하므로 Sα 의 크기와 Fz 에 영향을 받는다. 이러한 경향+ 을 분석하기 위해 식 (2)과 같이 차량 모델에 의한 영향 없이 항 상 유사한 결과를 확인할 수 있도록 μx ,μy 을 구해 [Fig. 5]에서 μx ,μy 와 Sα 의 관계를 분석하였다.
| (2) |
[Fig. 5]의 (a)는 Sα 에 따른 μx 의 변화로 각각의 지면의 마찰 계수에서 일정한 형태의 곡선을 이루고 있음을 알 수 있다. 이 곡선은 반비례와 형태와 유사하게 Sα 이 증가함에 따라 μx 가 감소하는 것을 확인할 수 있다. 다만 약 0°-3°구간에서는 슬립 이 매우 작아 Fx 이 순간적으로 측정되지 않기 때문에 급격히 증가하는 형태로 나타나 있고 Sα 이 약 30° 이후에는 일정 크기 를 유지하는 것을 확인하였다. 이를 통해 Pacejka Brush Model 에서 필요한 지면의 마찰계수와 횡 기울기 정보를 μx 을 이용 해 대체할 수 있다고 볼 수 있다[10]. 또한 Sα 에 따른 μy 의 관계 인 [Fig. 5]의 (b)에서 볼 수 있듯 μy 는Sα 이 발생하기 시작하는 0°-10°에서 급격히 증가하고 10°이후 일정하게 감소됨을 확인 했다. [Fig. 5]를 통해 이러한 사항을 종합하여 정리하면 μy 는 μx 의 크기에 비례하고 Sα 에 대해서도 비례하는 것 같으나 μx 와 Sα 의 관계에 의해 0°-10°에서 크게 증가하고 이후 미세하 게 감소하는 모습을 보여준다. 따라서 곡선을 설계하면 다음 과 같다. 이를 토대로 μy 의 추정 모델을 μx 와 Sα 을 변수로 하 여 다음과 같이 설계하였다.
| (3) |
| (4) |
| (5) |
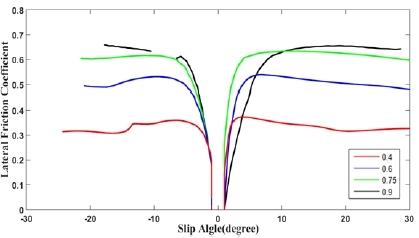
식 (3)은 앞으로 설계할 횡 방향 마찰계수 추정 모델인 최소 인자 횡 마찰 곡선(Minimal Argument Lateral Slip Curve, MALSC)의 기본적인 형태로 μy 의 대한 함수 f(Sa,μz) 는 Sα 에 대한 함수 g(Sa)와 μx 에 대한 함수 h(μx )로 구성되어 있 다. 식 (4)의 g(Sa)로 μx 와 Sα 의 관계를 나타내기 위해 Sα 에 따른 로그함수와 반비례함수로 설계하였다. 또한 μy 의 절댓 값은 0부터 1사이라는 전제조건을 위해 최댓값을 1로 맞추기 위한 상수 c1와 반비례함수로 인한 감소하는 최솟값 역할을 할 상수 c2로 구성하였다. 식 (5)의 h(μx )로 μy 가 μx 에 비례하 여 지면의 마찰계수에 따라 일정하게 나타나기 때문에 μx 와 전체적 크기를 조정하는 상수 c3의 곱으로 설계하였다. [Fig. 6] 은 Truck-sim에서 제공한 데이터를 이용하여 얻은 μy (좌)와 설 계한 MALSC을 이용하여 추정한 μy (우)를 비교하고 있다. MALSC을 이용하여 추정한 결과가 Truck-sim에서 제공한 데 이터와 비교할 때, 4가지의 마찰계수에서 모두 매우 유사함을 볼 수 있다. 따라서 μx 와 Sα 만을 이용하여 설계한 모델인 MALSC을 통해서도 Truck-sim에서의 사용한 Pacejka Brush Model와 비교하여 을 유사하게 추정이 가능함을 보여주고 있다.
2.3 시뮬레이션 결과 검증
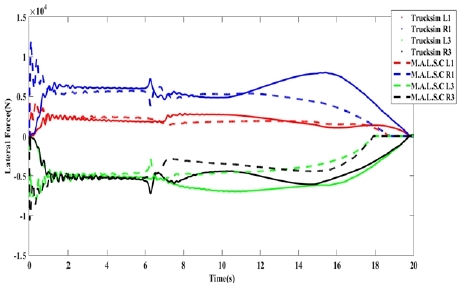
2.2절에서 설계한 MALSC의 타당성을 검증하기 위해 [Fig. 7] 에서는 앞서 4가지 지질에서의 주행 중에서 마찰계수가 0.6인 지면에서의 주행에 따른 을 보여주고 있다. Truck-sim에서 Pacejka Brush Model을 기반으로 출력한 데이터인 실선의 과 설계한 모델인 MALSC를 이용하여 추정한 점선의 을 비교하였다. 4개의 바퀴에서 제안한 MALSC를 이용하여 추 정한 결과가 전체적으로 방향성과 스케일 면에서 Truck-sim 에서 Pacejka Brush Model을 기반으로 출력한 데이터와 유사 한 것을 알 수 있었다.
3. 지질 분석 장치 실험
3.1 지질 분석 장치 실험 환경
2장의 시뮬레이션을 통해 설계한 MALSC을 실제의 야지환 경에 적용하기 위해 지면과 바퀴사이의 상호작용을 분석하기 위해 개발된 [Fig. 8]의 지형 분석 장치를 이용해 실험을 진행 하였다. 실험은 시뮬레이션에서 검증을 진행한 마찰계수 0.6 과 유사한 마찰계수를 가지고 있는 자갈에서 0°-90°에서 5°씩 Sα 을 증가시키며 진행하였다.
3.2 간략화 횡 마찰 곡선 보정
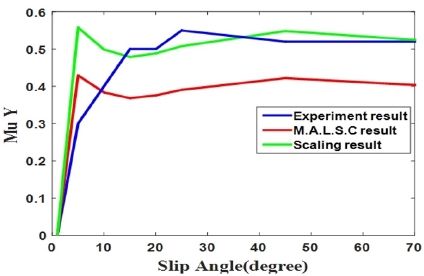
[Fig. 9]는 지질 분석 장치를 이용하여 실험 결과를 분석한 그래프이다. 그래프에는 Sα 에 따른 μy 로 총 3가지의 결과를 보여주고 있다. 파란색 그래프는 지질 분석 장치에 설치된 F/T 센서를 이용해 바퀴와 지면사이의 힘을 측정하여 만든 결과이 고, 붉은색 그래프는 Truck-sim을 이용해 설계한 MALSC으로 추정한 μy 이다. 두 그래프에는 일정 오차가 존재하는데 이는 실제 지질과 시뮬레이션의 차이로 볼 수 있다. 따라서 이를 개 선하기 위한 스케일링이 필요함을 알 수 있다.
| (6) |
식 (6)은 식 (3)에 시뮬레이션과 실제 지질의 차이를 보정하 기 위한 스케일 상수 k를 곱해주었다. 이를 출력한 결과가 [Fig. 9]의 초록색 그래프이다. 보정 상수를 통해 시뮬레이션과 실 제 지질의 오차를 줄일 수 있었다. 다만 슬립각의 범위가 0°-10°에서 급격하게 증가하는 μy 의 특성을 실험장치의 한계 로 정확히 분석하기 어려움이 있었으며, F/T센서를 통한 횡 방 향 힘의 측정에 어려움이 있어 반복적인 실험을 통해 평균적 인 결과를 사용하여 당초 예상보다 측정값이 낮게 나타나고 있다. 이는 추후 추가적인 실험을 통해 개선해야 될 사항이다.
4. 야지환경에서의 로봇 주행 실험
4.1 실외 로봇 주행 실험
본 논문의 3장에서의 실험 결과를 토대로 모래와 자갈로 이 루어진 실외의 야지환경에서 국방과학연구소의 견마로봇을 이용한 주행실험을 진행하였다. 실제 로봇 주행실험은 모래와 자갈로 이루어진 로봇주행실험장에서 진행되었으나 시뮬레 이션과 달리 센서의 노이즈 및 오차로 인해 바퀴에서 발생하 는 힘의 참값과 지면의 마찰계수 정보를 정확히 알 수 없으므 로 아래와 같이 가정을 설정하여 결과를 분석하였다.
첫째, 주행하는 지면의 마찰계수의 참값을 알 수 없으므로 지질에 따른 마찰계수 추정의 선행연구의 결과에 따라 0.6에 서 0.1의 오차 범위 내에서 타당성이 있는 마찰계수를 추정한 다고 볼 수 있다[11,12].
둘째, 바퀴에서 발생하는 의 힘의 경우 Friction Circle, Pacejka Brush Model, 마찰 모델 수식을 이용해 각각 추정한 결 과의 참값은 논하지 않는다. 이때, Pacejka Model을 추정하는 데 있어 필요한 요소인 지면의 마찰계수는 초기의 값을 0.6으 로 하고 매 순간 추정한 마찰계수를 다음 추정에 사용한다.
셋째, 바퀴에서의 수직 힘의 경우 각 서스펜션의 변위를 이 용해 추정한 결과를 사용한다.
넷째, 각 바퀴의 기구학적 위치 때문에 추정결과가 동일하 지 않을 수 있지만 ,동일한 환경에서 추정한 결과이기 때문에 각 바퀴에서의 추정한 마찰계수의 분산이 작을수록 추정 결과 의 신뢰도가 높다고 본다.
4.2 제자리 회전 주행 실험 결과
먼저 각 바퀴에서 슬립각이 일정하게 발생하는 제자리 회 전 주행을 진행하여 μy 과 마찰계수 추정결과를 비교하였다.
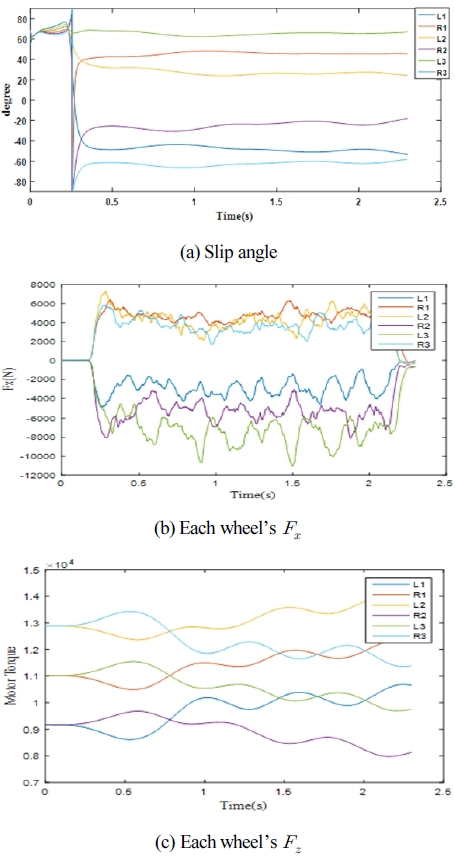
[Fig. 10]은 (a)은 6 바퀴에서 발생한 슬립각을 의미하고, 이때 의 Fx , Fz 을 [Fig. 10]의 (b), (c)에서 확인할 수 있다.
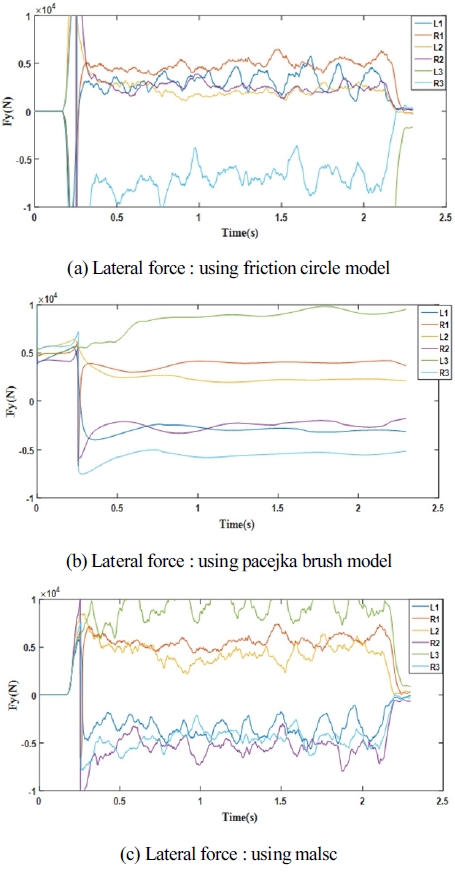
[Fig. 11]은 각각 Friction Circle Model, Pacejka Brush Model, MALSC을 이용해 추정한 의 결과이다. Friction Circle Model 방식을 이용한 결과 Sα 이 45° 이상으로 넘어갈 경우 추 정 값이 발산하며 Sα 의 방향성과 다르게 추정될 수도 있음을 확인하였다. 반면 Pacejka Brush Model과 제안한 MALSC을 이용한 추정에서는 Sα 의 방향성에 맞는 결과를 보여주며 두 추정 방식의 결과가 유사하다. 그러나 Pacejka Brush Model은 시간이 변화에 따라 큰 변화가 없이 일정한 결과를 보여주는 데 이는 추정에 필요한 인자의 일부를 가정과 같이 미리 제한 한 것의 영향을 받았기 때문이다. 반면에 제안한 MALSC은 매 순간 값의 변화가 눈에 띄게 나타는데 이는 MALSC이 Fx , Fz 의 영향을 받기 때문이다. 따라서 Fx , Fz 이 매 순간 변하고 이 를 반영하여 을 추정한 MALSC이 추정 결과의 타당성도 있 으며 Pacejka Brush Model에 비해 실시간성을 띄고 있음을 보 여주고 있다.
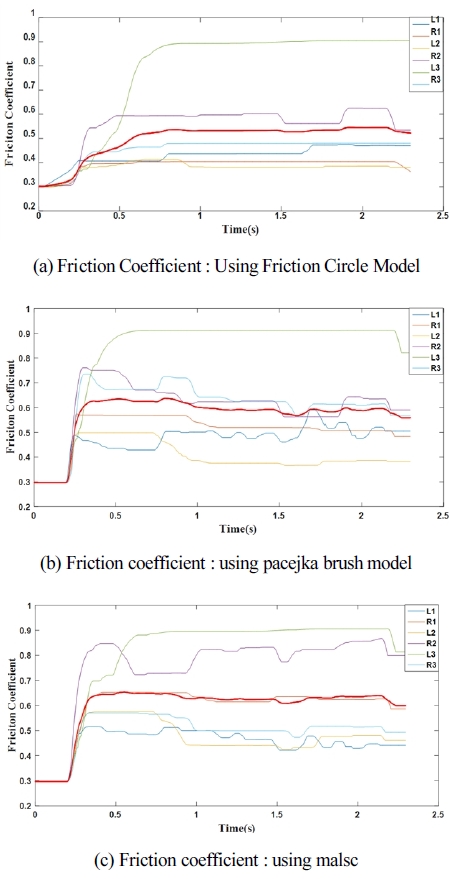
[Fig. 12]는 Friction Circle, Pacejka Brush Model, 본 논문에 서 제안한 MALSC을 통해 각 바퀴에서 추정한 지면의 마찰계 수이다. 그래프의 붉은색의 굵은 실선은 전체 바퀴의 평균으 로 가정에 따라 로봇이 주행한 지면의 마찰계수를 뜻한다.
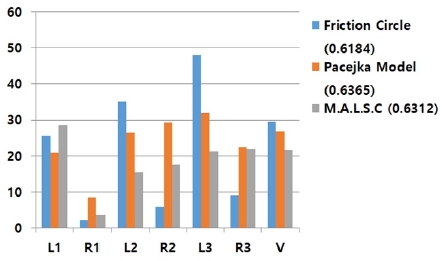
[Fig. 13]는 데이터를 직관적으로 볼 수 있도록 그래프로 표 현한 것으로 Friction Circle, Pacejka Brush Model, 그리고 본 논 문에서 제안한 MALSC을 통해 추정한 을 이용하여 마찰계 수를 추정한 결과이다.
지면의 마찰계수는 각 바퀴에서 추정한 마찰계수의 평균으 로 하여 각 방식에서 추정한 지면의 마찰계수 값을 보여주고 있다. 가정의 범위 내에서 3가지의 추정 방안 모두 의미가 있 는 마찰계수를 추정하고 있음을 확인할 수 있다. 또한 3가지 방식의 성능에 대한 결과 분석을 위해 각 방식의 평균에서의 각 바퀴의 오차율과 이에 따른 분산을 보여주고 있다. 실험에 서 지면의 마찰계수의 참값을 알 수 없기 때문에 앞선 가정에 따라 각 바퀴에서 추정한 값의 분산이 작을수록 추정 신뢰도 가 높고 이 신뢰도에 따라 추정방안의 성능을 평가하게 된다. [Fig. 13]의 그래프에서도 알 수 있듯이 전체적으로 제안한 MALSC이 다른 두 방식에 비해 각 바퀴의 분산이 작은 것을 알 수 있다. 이는 3가지 방식에서 추정한 마찰계수가 비슷하더 라도 각 바퀴에서 추정한 값이 유사하게 추정된 MALSC이 마 찰계수의 추정 신뢰도가 높다 볼 수 있다.
4.3 시험 경로 주행 실험 결과
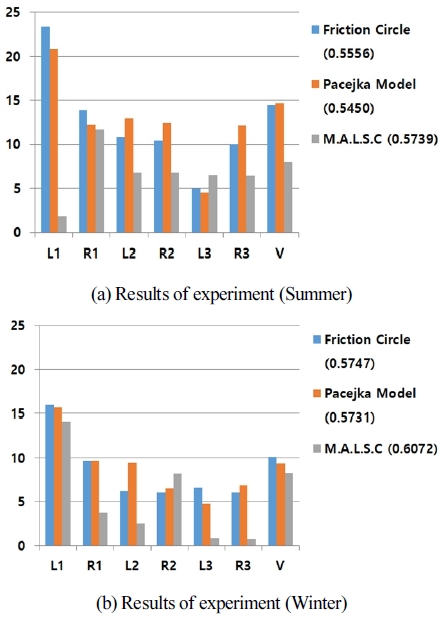
4.2절의 제자리 회전 주행처럼 Slip Angle이 충분히 발생하 는 상황뿐만 아니라 일반적인 경로 주행 실험을 통해 제안한 MALSC의 검증하였다. 제안한 MALSC이 다양한 지질환경에 서 적용할 수 있는지 여부를 판단하기 위해서는 여러 장소에 서 실험을 진행해야 하지만 실험의 여건상의 어려움으로 인해 여름과 겨울의 계절의 차이를 둔 실험 결과로 추가적으로 비 교를 진행하였다. 일반적으로 모래와 흙으로 이루어진 지질의 경우 여름에는 습윤하여 지면의 부드럽기 때문에 지면의 반발 력이 건조하고 지면이 단단한 겨울의 경우보다 낮게 마찰계수 가 추정된다고 선행연구를 통해 알 수 있다. [Fig. 14]은 로봇이 주행한 경로로 완만한 곡선으로 이루어진 경로를 주행을 통해 실제의 로봇이 주행하는 일반적인 상황에서의 실험을 진행하 였다. 이때, 주행 경로가 완만한 곡선이기 때문에 가 1000 N 이하로 로봇의 규격에 비해 매우 작은 크기로 추정되어 추정 결과를 비교하지 않고 마찰계수의 추정에 대한 검증만 진행하 였다. [Fig. 15]는 여름과 겨울에 각각 진행한 실험의 결과로 [Fig. 13]와 같은 방식으로 결과를 비교하였다.
[Fig. 15]의 (a)는 여름에 진행한 실험의 결과로 L3 바퀴에서 추정 결과의 오차율이 MALSC방식이 높게 나왔지만, 나머지 바퀴의 오차율과 전체의 분산이 전부 낮게 나타났으며 그 값 이 전체적으로 비슷하기 때문에 지면의 마찰계수 추정에 대한 신뢰도가 제자리회전과 마찬가지로 다른 추정 방안에 비해 높 다고 볼 수 있다.
물론 Pacejka Brush Model의 필요한 인자의 정보가 정확히 주어졌다면 마찰계수 추정 신뢰도가 높을 수 있지만 그렇지 않았기 때문에 MALSC를 이용해 횡 방향 힘을 추정했을 때 각 바퀴의 마찰계수의 편차가 적고 추정결과의 신뢰도가 더 높은 것을 확인 할 수 있었다. [Fig. 15] 의 (b)는 겨울에 진행한 실험 에 대한 결과로 R2바퀴를 제외하고 여름에 진행한 실험의 결 과와 각각의 방식이 유사한 결과를 보여주는 것을 확인할 수 있다. 흥미롭게도 겨울에 진행한 실험의 경우 여름에 진행한 실험에 비해 전체적으로 오차율이 적게 추정되었는데, 이는 마찰계수를 추정하기 위해 사용한 근본적인 방안이 지면의 물 리적 변화에 따른 추정법인 브리시우스 모델에 기반을 두고 있기 때문에 물리적으로 지면이 단단한 겨울에 추정 정밀도가 여름에 비해 높은 것으로 볼 수 있다. 또한 겨울에 진행한 실험 결과에서 여름에 진행한 실험보다 마찰계수가 평균적으로 10%가량 증가한 것으로 보아 실험을 통해 추정한 마찰계수가 의미 있는 결과임을 보여주고 있다.
5. 결 론
본 논문에서는 바퀴와 지면사이의 횡 방향 힘을 추정하는 데 있어 실시간으로 획득하기 어려운 사전 정보와 많은 인자 들을 요구하는 추정 방식에서 즉각적으로 추정이 가능한 최소 한의 인자들을 이용하여 기존과 유사한 성능을 가진 MALSC 을 설계하여 횡 방향 힘을 추정할 수 있도록 하였다. 모델을 설 계하기 위해 시뮬레이션과 실험을 통해 횡 방향 힘과 관련된 요소를 분석하고 , 설계된 모델의 검증을 위해 기존의 추정 방 법과 비교를 통해 검증하였다. 또한 최초의 목적에 맞게 실제 야지 환경을 주행하는 로봇을 통해 기존의 마찰 원과 Pacejka Brush Tire Model을 이용한 방식과 추정결과를 비교해 실제 로 봇에 적용이 가능함을 검증하였다. 이를 통해 최종적으로 로 봇이 주행하는 동안 각 바퀴에서 추정한 마찰계수의 분산이 기존보다 작도록 하여 지면에 대한 마찰계수 추정결과의 신뢰 도를 높여주는 결과를 보여주었다.
Acknowledgments
This research was supported by Agency for Defense Development (UD150021ID)
References
-
R. Welch, D. Limonadi, and R. Manning, “Systems Engineering the Curiosity Rover: A Retrospective,” 2013 8th International Conference on System of Systems Engineering, Maui, HI, USA, pp. 70-75, 2013.
[https://doi.org/10.1109/SYSoSE.2013.6575245]

-
C. Ahn, H. Peng, and H. E. Tseng, “Robust estimation of road friction coefficient,” IEEE Transactions on Control Systems Technology, vol. 21, no. 1, pp. 1-13, Jan., 2013.
[https://doi.org/10.1109/TCST.2011.2170838]

-
J. Y. Kim and J. Lee, “Ground Surface Identification for Mobile Robots on Rough Terrain, based on the Estimation of Soil Resistance,” Journal of institute of control robotics and systems, vol. 23, no. 3, pp. 186-193, 2017.
[https://doi.org/10.5302/J.ICROS.2017.16.0211]

-
J. Y. Kim and J. Lee, “Traction-energy balancing adaptive control with slip optimization for wheeled robots on rough terrain,” Cognitive Systems Research, Vol 49, pp. 142-156, June, 2018.
[https://doi.org/10.1016/j.cogsys.2018.01.007]

-
C.-S. Kim, J.-O. Hahn, K.-S. Hong, and W.-S. Yoo, “Estimation of Tire–Road Friction Based on Onboard 6-DoF Acceleration Measurement”, Vehicular Technology IEEE Transactions on, vol. 64, pp. 3368-3377, 2015.
[https://doi.org/10.1109/TVT.2014.2358616]

-
Y.-H.J. Hsu, S.M. Laws, and J.C. Gerdes, “Estimation of tire slip angle and friction limits using steering torque,” IEEE Transactions on Control Systems Technology, vol. 18, no. 4, pp. 896-907, July 2010.
[https://doi.org/10.1109/TCST.2009.2031099]

- H. B. Pacejka, Trie and vehicle dynamics, 3rd ed. Butterworth- Heinemann, 2002, pp. 59-446.
-
K. B. Singh and S. Taheri, “Estimation of tire–road friction coefficient and its application in chassis control systems,” Systems Science & Control Engineering, vol. 3, no.1, pp. 39-61, 2015.
[https://doi.org/10.1080/21642583.2014.985804]

-
J. Kang, W. Kim, J. Lee, and K. Yi, “Skid Steering based Driving Control of a Robotic Vehicle with Six In-Wheel Drives,” Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, vol. 224, no. 11, pp. 1369-1391, 2010.
[https://doi.org/10.1243/09544070JAUTO1405]

-
J. Nah, J. Seo, K. Yi, W. Kim, and J. Lee, “Friction circle estimation-based torque distribution control of six-wheeled independent driving vehicles for terrain-driving performance,” Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, Vol. 229, no. 11, pp. 1469-1482, 2015.
[https://doi.org/10.1177/0954407014564780]

-
G. Erdogan, L. Alexander, and R. Rajamani, “Friction coefficient measurement system for autonomous winter road maintenance,” Vehicle System Dynamics, vol. 47, no. 4, pp. 497–512, 2009.
[https://doi.org/10.1080/00423110802220554]

-
R. Ghandour, A. Victorino, M. Doumiati, and A. Charara, “Tire/road friction coefficient estimation applied to road safety,” 18th Mediterranean Conference on Control and Automation, Marrakesh, Morocco, 2010, doi: 10.1109/MED.2010.5547840.
[https://doi.org/10.1109/MED.2010.5547840]

1983 서울대학교 전자공학과(공학사)
1985 한국과학기술원 전기 및 전자공학과 (공학석사)
1991 한국과학기술원 전기 및 전자공학과 (공학박사)
1994~현재 충남대학교 메카트로닉스 공학 과 교수
관심분야: 야지 주행 로봇, 로봇 위치 추정, 해양 로봇 유영, 양팔 로봇 제어