자율수상선을 이용한 수중 자기장 지도 작성
© Korea Robotics Society. All rights reserved.
Abstract
Geomagnetic field signals have potential for use in underwater navigation and geophysical surveys. To map underwater geomagnetic fields, we propose a method that exploits an autonomous surface vehicle. In our system, a magnetometer is rigidly attached to the vehicle and not towed by a cable, minimizing the system’s size and complexity but requiring a dedicated calibration procedure due to magnetic distortion caused by the vehicle. Conventional 2D methods can be employed for the calibration by assuming the horizontal movement of the magnetometer, whereas the proposed 3D approach can correct for horizontal misalignment of the sensor. Our method does not require a supporting crane system to rotate the vehicle, and calibrates and maps simultaneously by exploiting data obtained from field operation. The proposed method has been verified experimentally in inland waters, generating a magnetic field map of the test area that is of much higher resolution than the public magnetic field data.
Keywords:
Autonomous surface vehicle (ASV), Underwater mapping, Magnetic field, Calibration1. 서 론
지구자기장 또는 지자기는 지구 외핵의 회전 동역학적 운 동(geodynamo)에 의해 발생하는 지구 물리 신호로써 태양풍 으로부터 지구를 보호하는 중요한 역할을 하고 있다. 이러한 지구자기장은 수중에서도 유용하게 사용될 수 있는데, 수중이 동체의 관성항법, 해저의 UXO (unexploded ordnance) 검출, 판 의 이동 분석과 같은 것들이 그 예이다[1-4]. 지자기 지도는 온라 인 상에 공시되기도 하는데 NGDC (National Geophysical Data Center), IAGA (International Association of Geomagnetism and Aeronomy)와 같은 기관에서는 WMM (World Magnetic Model)[5], IGRF (International Geomagnetic Reference Field)[6]와 같은 모 델들을 주기적으로 제공하고 있다. 하지만 이러한 공시 모델들 은 해상도가 매우 낮으며 고해상도의 HDGM (High Definition Geomagnetic Model)과 같은 모델은 추가적인 비용이 필요하 고 이 또한 정확도 및 업데이트 주기에는 한계가 있다. 때문에 본 논문에서는 국내 연안과 같은 관심 해역에 대해 고해상도 의 지자기 지도를 구축할 수 있는 기술을 개발하고자 한다.
지구자기장의 관측에는 항공/위성 관측이 많이 사용되며 해양 환경에 대해서는 선박이 주로 사용되는 방법이다[7-9]. 선 박의 경우 센서를 케이블로 견인(towing)하는 형태를 많이 사 용하게 되는데 이 경우 센서가 선박의 추진기와 멀리 떨어져 있으므로 외부의 간섭이 적은 대신 케이블로 인해 선박의 경 로가 제한되고, 견인되는 센서모듈의 정확한 위치와 자세 추 정을 위해 별도의 케이블 거동 분석이 필요하다는 단점이 있 다. 본 논문에서는 자율수상선(Autonomous surface vehicle, ASV)을 이용한 수중 자기장 측정에 있어 자력계를 견인이 아 닌 수상선 본체 아래에 직접 설치하여 사용하고자 한다. 이를 통해 전체적인 시스템을 단순화시키고, 수상선의 경로 생성에 있어 자유도를 높여 지도 작성의 효율성을 높이고자 한다. 하 지만 이 경우 수상선과 자력계가 가까워진 만큼 수상선의 전 장부에 의한 왜곡 보정이 필요하게 되는데 수상선 같은 큰 시 스템은 일반적인 자력계 보정에서 요구되는 3축 방향 회전이 어렵기 때문에, 본 논문에서는 맵핑 영역을 주행한 데이터를 가지고 지자기 맵핑과 자력계 보정을 동시에 수행할 수 있는 방법을 제안하고자 한다.
2. 수상선 기반 자기장 지도 작성
2.1 하드웨어 시스템
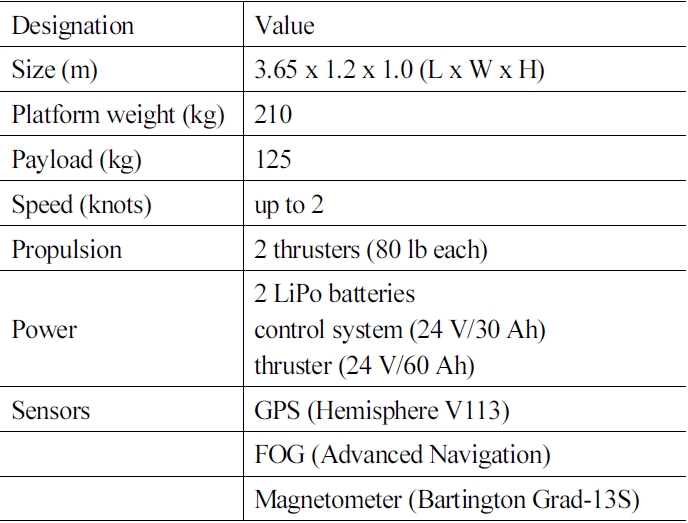
수중 환경 정보 획득을 위해 자체 개발된 자율수상선은 [Fig. 1]과 같다. 수상선은 쌍동선 타입으로 자세한 제원은 [Table 1]에 표시하였다. 주요 시스템은 전원 및 추진부, GPS 와 AHRS기반의 항법 및 제어부, 원격 통신부, 계측 센서의 데 이터 처리부로 구성되어 있으며, 육상 제어실에서 원격으로 제어하고 상태를 실시간으로 관제할 수 있도록 구성되었다. 또한, 자율수상선의 경유점 추종 제어를 위해 시선각(line of sight) 및 수선 경로(cross track) 유도 법칙을 적용한 제어기를 설계하여 구현하였다.
자기장을 측정하는 센서인 자력계는 크게 자기장의 세기 (F)를 측정하는 스칼라 센서 또는 3차원 자기장 벡터 m=[m x, m y, m z]T를 측정하는 벡터 센서로 나눌 수 있다. 본 논문에서는 fluxgate 타입의 벡터 센서를 사용하였으며 이 경우 센서값은 고정좌표계(Body-fixed frame, BFF)에서 측정된 자기장 값이 기 때문에 참조좌표계(Reference frame) 상에서 표현하기 위해 서는 별도의 자세 정보가 있어야 한다. 이를 위해 수상선 시스 템에 별도의 자세 센서도 장착하여 측정된 지자기 벡터의 참 조좌표계로의 전환이 가능하도록 하였다. 본 논문에서는 광섬 유 자이로스코프(fiber optic gyroscope, FOG)를 사용하였으며 획득된 자세정보는 3차원 자기장 캘리브레이션에서도 사용 되었다. 이에 대한 자세한 내용은 다음 절에서 소개한다.
2.2 자력계 보정
자력계의 경우 주변의 자성체 또는 전자장으로 인해 왜곡 된 관측을 하게 되는데 이를 적절히 보정하지 않으면 실제 자 기장 값을 얻을 수 없다. 본 연구에서 자기장 센서는 수상선과 일정 간격 떨어지도록 부착되었지만 여전히 수상선의 전장부 와 추진기에 의해 영향을 받기 때문에 보정이 필요하다. 일반 적인 자력계 보정은 1) 센서를 3축으로 자유롭게 회전한 후 2) 관측값이 이루는 타원체를 원점 중심 구로 변환하는 과정을 통해 이뤄진다[10]. 하지만 수상선과 같은 거대한 시스템의 경 우 크레인과 같은 특별한 장비가 없으면 1축의 회전도 어렵다. 때문에 본 논문에서는 별도의 전방위 회전 단계 없이 수상선 이 주행 중 획득한 자력계 데이터를 가지고 보정과 지도작성 을 동시에 수행하는 방법을 제안하고자 한다.
자력계의 2차원 보정은 Alotta [11]가 제안한 것으로 운동체 가 수평면 상에서 움직인다는 가정 하에 자력계를 보정하고, 이를 방향각(heading) 추정에 사용한 방법이다. 수상선 역시 yaw 방향 변위가 지배적이라는 가정 하에 이 방법을 적용할 수 있다. 수상선이 yaw 변위가 충분히 발생하는 임의의 경로 로 주행했을 때 자력계 값의 3차원 궤적은 이상적으로 구 위의 수평 원을 생성하게 되어 있다. 하지만 hard iron 왜곡, soft iron 왜곡, 센서 스케일 인자 오차와 같은 자력계 왜곡에 의해 실제 센서값은 [Fig. 2(a)]에 나와 있는 것처럼 타원체 위의 타원 (E raw)을 생성한다. 이를 수평면 상에 사영(projection)시켜 새 로운 타원(E1)을 얻은 후 다시 단위 원(C1)으로 변환하면, 방향 각 추정에 대한 자력계 왜곡을 보정할 수 있다. 이에 대한 자세 한 계산 과정은 아래와 같다.
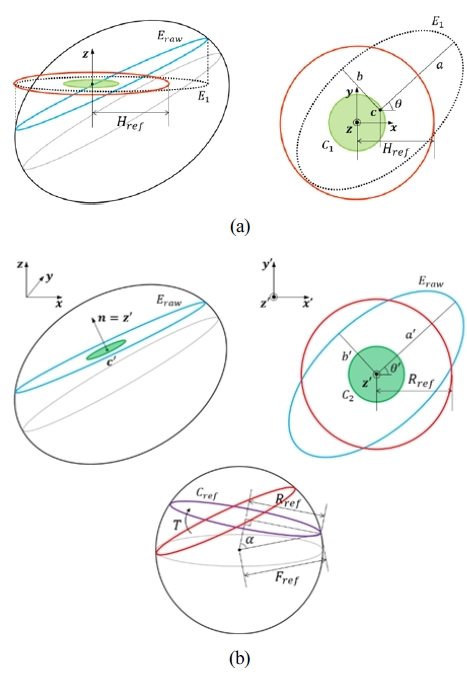
Two different calibration approaches. (a) 2D calibration by vertical projection. (b) 3D calibration with known orientation
| (1) |
| (2) |
| (3) |
| (4) |
여기서 nh는 E raw의 법선 벡터 n의 수평 방향 벡터이며, mh는 m의 nh방향 벡터, ϕ는 n과 z축과의 각도, m⊥는 m의 수직 방향 벡터, m∥는 m의 평행 방향 벡터, m2D는 단위원으로 보정된 자력계 관측값, Rz (∙)는 z축 방향 회전행렬, θ, a, b, c 는 각각 사영된 타원의 기울기, 장축, 단축 길이 및 중심점 좌 표이다. 한편, (4)의 단계에서 모든 자력계값은 단위 원을 기준 으로 보정되기 때문에(Hm2D ≈1) 실제 지자기 값을 구하기 위 해서는 적절한 스케일 인자를 다시 곱해주어야 한다. 본 논문 에서는 WMM에서 제공하는 H ref 값을 스케일 인자로 사용하 여 차원을 회복할 수 있도록 하였다.
| (5) |
앞에서 제시한 2차원 보정 방법에서는 이동체가 수평면 상 에서 움직인다고 가정하였다. 하지만 수상선의 경우 무게의 균형이 정확히 수평을 이루지 않을 수 있고 센서 역시 설치 시 에 부정합(misalignment)이 발생할 수 있다. 자력계는 이러한 자세 오차에 영향을 받아 편향(bias)된 측정을 하게 된다. 때문 에 수평 부정합까지 고려한 보정 방법이 필요하며 이를 위해 본 논문에서는 별도의 자세센서로부터 획득된 정보(roll, pitch, yaw)를 통해 참조가 되는 지자기 관측값을 생성, 이를 기준으 로 3차원 보정을 하는 방법을 제안한다. 제안된 보정 방법은 [Fig. 2(b)]에 나타내었으며 자세한 계산 과정은 아래와 같다.
| (6) |
| (7) |
| (8) |
여기서 m ref는 참조 지자기 관측값으로, WMM에서 제공 하는 지자기 벡터 를 자세센서로부터 계산되는 를 이용하여 센서 좌표계로 변환하여 구한다. 식 (7)-(8)에서는 실제 관측값 m에 대해 PCA를 수행하여 얻은 m′을 기준으로 단위원(C2)화 과정을 거치고, 그 결과에 스케일 인자 R ref를 곱하였다. 여기서 θ′ , a′ , b′는 각각 PCA 타원의 기울기, 장축, 단축 길이이다. R ref값은 다음과 같이 계산할 수 있다.
| (9) |
| (10) |
여기서 F ref는 참조 지자기의 세기 값, 는 i번째 참조 지자기 관측값, n ref는 원 C ref의 법선 벡터, N은 관측값의 개 수이다. 끝으로 와 m ref 사이의 3차원 변환 을 구함으로써 자력계의 3차원 보정값 m3D를 구할 수 있다.
| (11) |
| (12) |
3차원 변환에는 최소근평균자승법(least root mean square, LRMS)인 Kabsch 알고리즘[12]을 사용하였다.
2.3 지자기 지도 생성
앞서 제시한 방법을 통해 우리는 센서고정좌표계(BFF) 상 에서 보정된 자력계 값을 계산할 수 있었다. 하지만 실제 항법 이나 탐사를 위해서는 모든 지자기 값이 임의의 약속된 참조 좌표계 상으로 변환되어야 한다. 또한 이렇게 변환된 지자기 지도는 수상선의 경로를 따라서만 생성되므로, 조밀한 지도를 얻기 위해서는 미탐색 영역에 대한 보간도 필요하다. 이에 대 한 내용을 다음에서 설명한다.
본 논문에서는 편의상 UTM 좌표계를 참조좌표계로 사용 하였는데 이 외에 다른 국지/전역 좌표계(NED, ECEF 등)도 사 용될 수 있다. 지자기값의 센서고정좌표계에서 UTM 좌표계 로의 변환은 아래와 같이 구할 수 있다.
| (13) |
자기장 벡터 mUTM은 또한 널리 사용되는 지자기 표현법인 F (total strength), D (declination), I (inclination)의 세 요소로 나타낼 수 있으며 이의 변환 과정은 아래와 같다.
| (14) |
| (15) |
| (16) |
수상선의 주행으로 초기 생성된 듬성(sparse)한 지도의 조 밀화를 위해 본 논문에서는 비매개변수 회귀법 중 하나인 가 우시안 프로세스 회귀(Gaussian process regression, GPR)[13]를 사용하였다. GPR에서는 아래 식 (17)과 같이 함수의 확률분포 를 함수의 평균(μ)과 분산(Σ)을 통해 정규분포로 정의하고, 커널 K의 설계를 통해 대상 정의역 x′에 대한 함수의 회귀를 수행한다. 본 논문에서는 식 (19)와 같은 비교적 단순한 squared exponential (SE) 커널을 적용하였다.
| (17) |
| (18) |
| (19) |
여기서 δ(∙)은 Kronecker delta 함수, σf, l, σn은 커널 파라 미터들이다.
3. 실험 결과
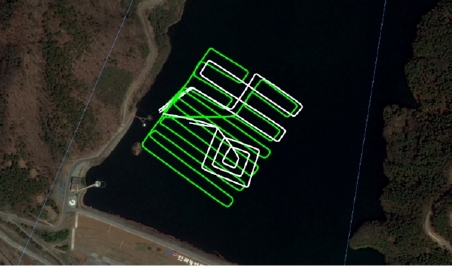
제안된 수상선 시스템으로 지자기 지도 작성을 검증하기 위해 내수면 실험을 수행하였다. [Fig. 3]은 실험 영역인 전남 장성호(35°21'30.2"N, 126°49'17.7"E)의 위성 사진 및 수상선 의 주행 경로를 보여주고 있다. 수상선은 약 400 m x 400 m 영 역에서 총 5회의 자율 주행을 통해 데이터를 획득하였는데 수 상선에 장착된 추진기의 급격한 속도 변화에 따른 지자기 정 보의 왜곡을 최소화하기 위해 국소 영역 내에서 사전에 설정 한 경유점들을 일정한 속도로 경유하며 운항하도록 두 추진기 의 회전속도를 제어하였다. 그리고 지자기 지도 생성을 위해 각 경유점간의 직선 거리에 최대한 근접하여 일정한 간격으로 지자기 정보를 계측하는 것이 중요하므로, 목표 경유점이 변 경되는 시점에서는 시선각 유도 법칙에 큰 가중치를 적용하였 고, 목표 경유점에 접근할수록 수선 경로 유도 법칙에 가중치 를 상대적으로 크게 적용하였다. 이와 같은 유도 법칙을 기반 으로 계산된 오차를 최소화하기 위해 선미에 고정된 두 추진 기의 회전 속도를 PD (proportional derivative) 제어기를 통해 제어하였으며, 그 실험 결과로 경유점간의 직선 거리에 빠르 게 수렴함을 보였다. 이 때의 수상선은 평균적으로 1.5 노트 (knots)의 운항 속도로 경유점간 직선 거리 대비 수선 경로 오 차는 약 2 m 정도를 유지한 상태로 운항하며, 지자기 정보를 계측하였다.
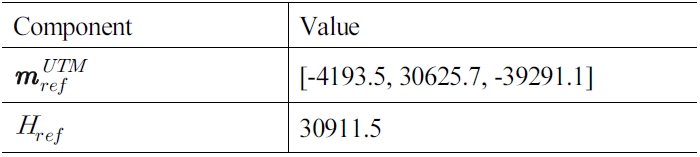
지도 작성을 위해 수상선에 설치된 센서는 [Table 1]에 표시 된 것과 같다. 모든 센서 데이터는 수상선 내의 PC에서 타임스 탬프와 함께 저장되었으며 MATLAB 환경에서 후처리 되었 다. 식 (5)-(10)에서 사용되는 참조 지자기 값은 실험 날짜에 해당 하는 실험 영역의 WMM 값을 사용하였으며 [Table 2]과 같다.
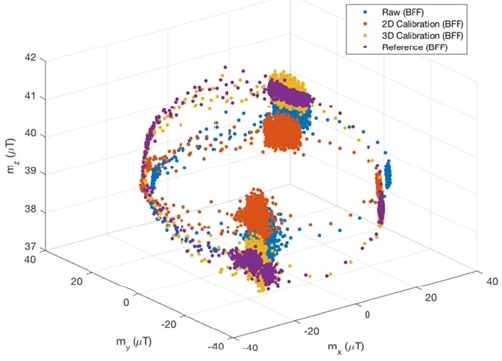
[Fig. 4]는 마지막 주행 경로에 대해 자력계의 미보정(raw) 관측값, 참조 지자기 관측값 m ref, 및 보정된 값들을 센서좌표 계 상에서 나타낸 것이다. 미보정 관측값의 경우 센서 왜곡으 로 인해 기울어진 타원 형태로 나타나며 참조 지자기 관측값 은 수상선 및 센서의 수평 부정합으로 인해 기울어진 원 형태 로 나타난다. 2차원 보정 결과는 미보정 관측값을 x-y 평면 상 에서 원점을 중심으로 하는 원으로 변환한 것으로 실험 영역 의 자기장 특성이 수평면을 기준으로 반영되어 있다. 하지만 실제 수상선은 센서의 무게와 센서 설치 오차로 인해 수평 부 정합이 발생하기 때문에 2차원 보정으로는 완전한 보정이 어 렵다. 반면에 제안된 보정 방법의 경우 참조 지자기 값을 기준 으로 3차원 상에서 변환을 수행함으로 수평 부정합까지 반영 할 수 있다. [Fig. 5]는 3차원 보정에 사용되는 R ref값을 계산하 는 과정으로, n ref를 통해 수상선과 센서의 수평 부정합을 확 인할 수 있다. 여기서 R ref값은 30899.7 nT로 계산되었다.
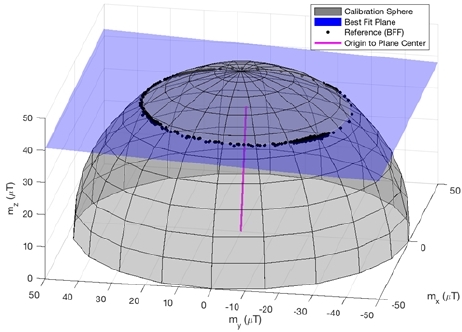
calibration sphere with m ref superimposed on it. The best fit plane and its normal vector represent the horizontal misalignment of the sensor frame
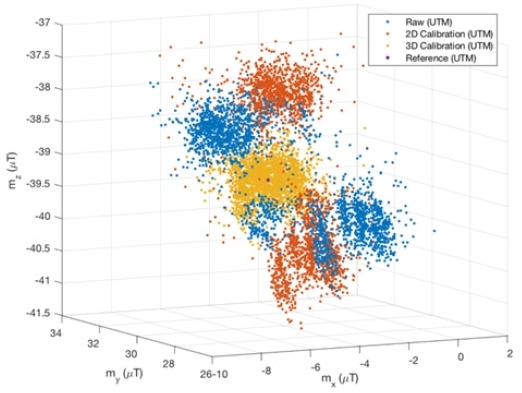
앞서 자력계 관측값을 센서좌표계 상에서 나타냄으로 자기 장 왜곡과 수평 부정합을 살펴보았는데, 참조 좌표계 상에서 는 보정의 결과를 더욱 자세히 확인할 수 있다. 참조 좌표계로 의 변환은 FOG에서 획득되는 자세 정보를 사용하였다. [Fig. 6]은 UTM 좌표계로 변환된 지자기 값들로 미보정 관측값과 2 차원 보정값의 경우 다봉형(multimodal)의 분리된 분포를 띄 는 반면, 3차원 보정이 적용된 값은 참조 자기장 값을 중심으 로 단봉형(unimodal)의 연속적인 분포를 띄고 있다. 실험지역 인 내수면의 지자기의 경우 약간의 구배는 존재하더라도 급작 스런 자기장의 도약(예로, 외부의 강한 전자기장으로 인한 영 향)은 없을 것이기 때문에 후자와 같은 분포를 띄는 것이 바람 직하며 이를 통해 제안된 보정 방법이 잘 동작하고 있음을 알 수 있다.
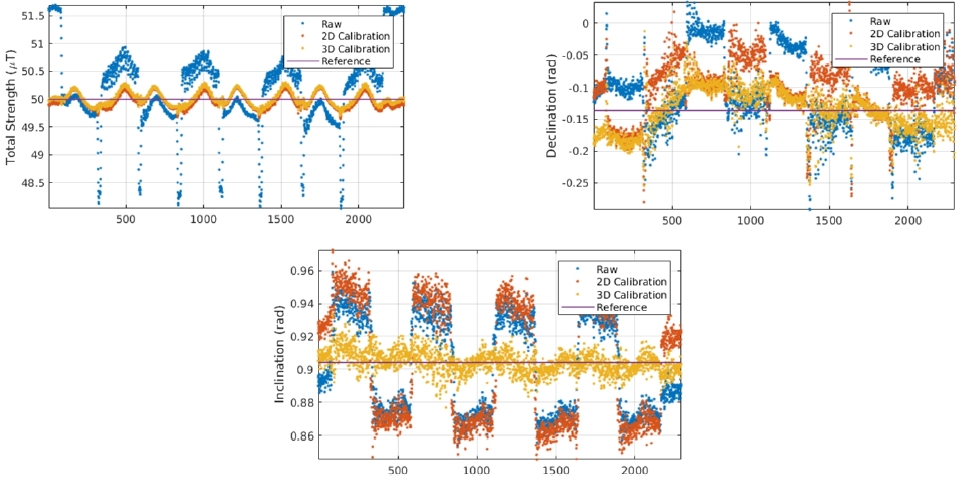
이렇게 참조 좌표계로 변환된 자력계 값을 다시 지자기 지 도 요소인 F, D, I로 생성한 결과는 [Fig. 7]과 같다. 여기서 2 차원 보정의 경우 F값은 보정이 되지만 D와 I값은 보정이 안 되고 있음을 알 수 있다. 반면에 3차원 보정의 경우 세 요소 모 두 참조 지자기 값을 기준으로 보정이 되는 것을 알 수 있다. [Fig. 8]은 F, D, I값을 NED 좌표계 상에서 나타낸 것인데, 미 보정 자력계 관측값의 경우 수상선 진행 방향에 따라 왜곡이 크게 발생함을 알 수 있다. 2차원 보정의 경우에는 앞서 설명 한 것과 같이 F만 주로 보정이 되었고 3차원 보정의 경우에만 모든 요소가 보정이 되었다.
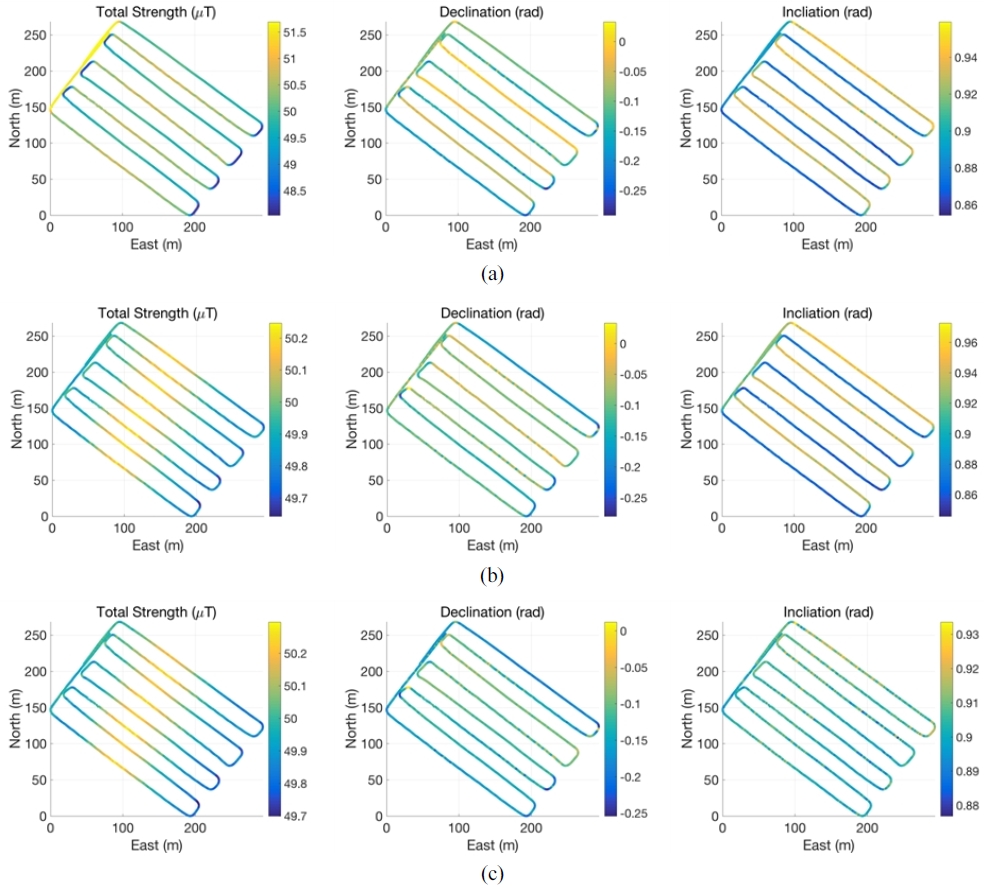
Magnetic field data mapped with vehicle trajectories in a NED coordinate system. (a) Raw, (b) 2-D calibrated, and (c) 3-D calibrated data. While raw and 2-D calibrated data suffer from orientation-dependent bias, 3-D calibration resolves it
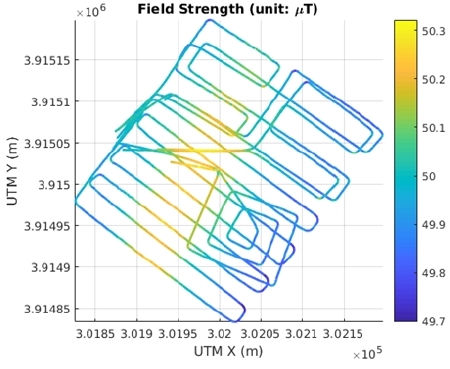
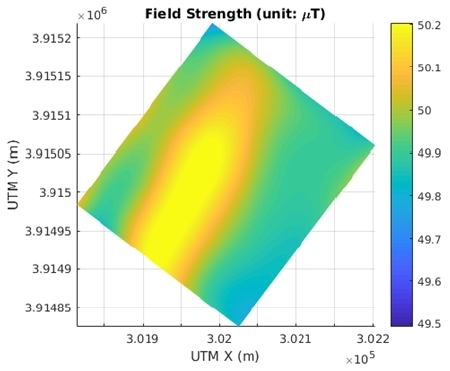
[Fig. 9]는 5회의 주행을 통해 획득된 F값들을 중첩하여 나 타낸 것이다. 이를 기반으로 미탐색 영역에 대한 GPR을 수행 한 결과는 [Fig. 10]과 같다. 탐색 영역의 가운데 부분에서 상대 적으로 높은 자기장 값을 관찰할 수 있는데 이는 호수 아래 지 각의 지구물리적 특성에 의한 것으로 추정된다. 공시된 지자 기 데이터 중 해상도가 높은 EMAG2-v3의 경우 격자 단위가 2 arcminute (약 3 km)인 것을 감안했을 때, 작성된 지자기 지도 는 높은 해상도를 가짐을 알 수 있다.
4. 결 론
본 논문에서는 수중에서의 자기장 지도 작성을 위한 자율 수상선 시스템 및 이를 이용한 지도 작성 방법에 대 해 제안하 였다. 특별히 수상선과 같은 대형 시스템에 자력계가 부착된 상태에서 크레인을 이용한 전방위 회전이 아닌 수상선이 주행 중 획득한 데이터를 이용하여 센서를 보정하는 방법을 제시하 였으며 이와 동시에 지자기 지도를 작성하는 방법을 제안하였 다. 또한 데이터 획득 시 발생하는 수상선 및 센서의 수평 부정 합을 고려하기 위해 별도의 자세 센서 값을 이용한 3차원 보정 방법을 제시하였다. 제안된 시스템은 전남 장성호에서의 내수 면 실험을 통해 검증되었으며 획득된 센서 값에 대한 3차원 보 정과 미탐색 영역에 대한 보간을 통해 실험 영역에 대한 최종 적인 자기장 지도를 생성하였다. 본 논문에서는 자력계 보정 에 중심을 둔 실험이 진행되었지만 향후 다양한 해역에서의 운영을 통해 수중 탐사 임무 수행 및 수중 항법을 위한 지자기 지도 구축에도 활용될 것으로 기대된다. 또한 제안된 보정 시 스템은 수상선 뿐만 아니라 글라이더와 같은 수중무인체계에 도 동일하게 적용이 가능할 것으로 기대된다.
Acknowledgments
This research was supported by a grant from Endowment Project of “Development of fundamental technologies on underwater environmental recognition for long-range navigation and intelligent autonomous underwater navigation” funded by Korea Research Institute of Ships and Ocean Engineering (PES9390).
References
- S. T. Tuohy, T. Maekawa, and N. M. Patrikalakis, “Interrogation of geophysical maps with uncertainty for AUV micro-navigation,” OCEANS’93, Victoria, BC, Canada, pp. 1181–1185, 1993.
-
F. C. Teixeira and A. Pascoal. “Magnetic Navigation and Tracking of Underwater Vehicles,” IFAC Proceedings Volumes, vol. 46, no. 33, pp. 239-244, 2013.
[https://doi.org/10.3182/20130918-4-JP-3022.00059]

-
Y. Pei and H. Yeo, “UXO Survey using Vector Magnetic Gradiometer on Autonomous Underwater Vehicle”, MTS/IEEE OCEANS 2009, Biloxi, pp. 1–8, 2009.
[https://doi.org/10.23919/OCEANS.2009.5422446]

-
M. A. Tivey and J. Dyment, “The Magnetic Signature of Hydrothermal Systems in Slow Spreading Environments,” Geophysical Monograph Series, by P. A. Rona et al. ed., vol. 188, AGU, Washington DC, pp. 43–66, 2010.
[https://doi.org/10.1029/2008GM000773]

- A. Chulliat, S. Macmillan, P. AIken, C. Beggan, M. Nair, B. Hamilton, A. Woods, V. Ridley, S. Maus, and A. Thomson, “The US/UK world magnetic model for 2015-2020: Technical Report,” National Geophysical Data Center, NOAA, doi: 10.7289/V5TB14V7.
-
C. C. Finlay, S. Maus, C. D. Beggan, T N. Bondar, A. Chambodut, T. A. Chernova, A. Chulliat, Y. P. Golovkov, B. Hamilton, M. Hamoudi, R. Holme, G. Hulot, W. Kuang, B. Langlais, V. Lesur, F. J. Lowes, H. Liihr, S. Macmillan, M. Mandea, S. McLean, C. Manoj, M. Menvielle, I. Michaelis, N. Olsen, J. Rauberg, M. Rother, T J. Sabaka, A. Tangborn, L. Tøffner-Clausen, E. Thébault, A. W. P. Thomson, I. Wardinski, Z. Wei, and T. I. Zvereva, “International geomagnetic reference field: the eleventh generation,” Geophysical Journal International, vol. 183, no. 3, pp. 1216–1230, December, 2010.
[https://doi.org/10.1111/j.1365-246X.2010.04804.x]

-
M. Engels, U. Barckhausen, and J. S. Gee, “A new towed marine vector magnetometer: methods and results from a Central Pacific cruise,” Geophysical Journal International, vol. 172, no.1, pp.115 –129, January, 2008.
[https://doi.org/10.1111/j.1365-246X.2007.03601.x]

-
J. S. Gee, S. C. Cande, “A surface-towed vector magnetometer,” Geophysical Research Letters, vol. 29, no. 14, 2002, doi: 10. 1029 2002GL015245.
[https://doi.org/10.1029/2002GL015245]

-
N. Isezaki, “A new shipboard three component magnetome-ter,” Geophysics, vol. 51, no. 10, pp. 1992–1998, 1986.
[https://doi.org/10.1190/1.1442054]

-
J. F. Vasconcelos, G. Elkaim, C. Silvestre, P. Oliveira, and B. Cardeira, “Geometric approach to strap down magnetometer calibration in sensor frame,” IEEE Transactions on Aerospace and Electronic Systems, vol. 47, no. 2, 1293–1306, April, 2011.
[https://doi.org/10.1109/TAES.2011.5751259]

-
B. Allotta, R. Costanzi, F. Fanelli, N. Monni, and A. Ridolfi, “Single axis FOG aided attitude estimation algorithm for mobile robots,” Mechatronics, vol. 30, pp. 158–173, 2015.
[https://doi.org/10.1016/j.mechatronics.2015.06.012]

-
W. Kabsch, “A solution for the best rotation to relate two sets of vectors,” Acta Crystallographica Section A, vol. 32, No. 5, pp. 922– 923, 1976.
[https://doi.org/10.1107/S0567739476001873]

-
C. E. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, The MIT Press, pp.7-31, 2006.
[https://doi.org/10.7551/mitpress/3206.001.0001]

2008 한양대학교 토목공학과(학사)
2010 KAIST 건설 및 환경공학과(석사)
2015 KAIST 건설 및 환경공학과(박사)
2016~현재 선박해양플랜트연구소 선임연구원
관심분야: 수중 환경 맵핑, 수중 로봇 항법
2005 충남대학교 메카트로닉스공학과(학사)
2007 충남대학교 메카트로닉스공학과(석사)
2016K AIST 기계공학과(박사)
2016~현재 선박해양플랜트연구소 선임연구원
관심분야: 해양로봇 자율운항, 영상 기반 센서융합