수정된 RLS 기반으로 관절 토크 센서를 이용한 로봇에 가해진 외부 힘 예측 및 펙인홀 작업 구현

1. 서 론

산업용 로봇은 프로그램 된 동작을 행함으로써 부품이나 장치, 도구 등을 움직일 수 있는 다 기능한 기계장치로 정의 되어져 있다. 로봇이 지속적으로 개발되고 연구되면서 현재 는 로봇의 활용도가 증대되고 인간의 능력을 대체할 수 있게 되었다. 로봇은 인간이 작업하기 어려운 환경에서도 작업이 가능하며 복잡하고 정밀도가 필요한 일을 반복적으로 할 수 있다^[1].

로봇을 단순히 반복작업 및 복잡한 작업의 대체 용도로 사 용한다면 외부 환경에 대한 고려 없이 지정된 경로를 잘 따라 움직일 수 있으면 된다. 하지만 주의 방해물이 있는 상황에서 의 반복 작업, 인간과의 협력 작업 환경, 펙인홀 작업과 작업물 체를 비틀기, 밀기, 자르기 등과 같은 작업에서는 로봇의 링크 및 엔드이펙터에서 외부 힘에 대해 인지하고 경로 수정 피드 백 제어를 할 수 있어야 한다. 이러한 이유로 로봇과 주변 환경 사이의 접촉 및 힘에 대한 정보를 얻는 것은 로봇을 제어함에 있어서 중요한 요소이다^[2-5].

로봇에 가해지는 외부 힘에 대한 정보를 얻기 위해 접촉 센 서, 힘/토크 센서, 토크 센서, 비전 센서 등의 다양한 센서가 연 구되며 사용되고 있다. 접촉 센서는 측정하고 싶은 특정부분 을 정하여 설치를 하거나 로봇 외부 전체에 설치를 하는 방법 으로 외부에서 가해지는 힘에 대해 측정 할 수 있다. 하지만 측 정 부위가 한정되거나 전체에 대해 설치할 경우 비용이 많이 드는 단점이 있다. 힘/토크 센서는 로봇의 베이스나 엔드이펙 터의 끝에 설치가 되며 로봇에 가해지는 전반적인 힘 혹은 엔 드이펙터 끝에 설치가 되며 로봇에 가해지는 전반적인 힘 혹 은 엔드이펙터에 가해지는 힘과 토크에 대한 정보를 쉽게 얻 을 수 있다. 엔드이펙터에서 가해지는 힘에 대한 정보를 쉽게 얻을 수 있기 때문에 작업물체에 힘을 가하여 가공하는 작업 에 용이하다. 하지만 로봇의 몸체 중간에 가해지는 힘에 대한 정보를 정확히 얻기 어려우며 범용적으로 사용되기에는 비용 이 다른 센서에 비해 비싸다. 토크 센서는 관절 로봇의 각 관절 에 설치가 되며 관절에 걸리는 토크를 측정할 수 있다. 다관절 로봇의 경우 각 조인트에 걸리는 토크를 통해 각 관절 사이의 링크, 엔드이펙터에 걸리는 외부 힘에 대한 측정이 용이하며 유연관절로봇의 관절 처짐 현상에 대한 제어를 할 수 있는 중 요 요소이다. 하지만 로봇의 각 관절 및 링크의 진동, 제어 상 태 등에 의해 오차가 발생 할 수 있으며 로봇 구조 설계가 복잡 하다^[6-9].

힘 측정 장비 없이 로봇에 가해지는 외부 힘을 예측하기 위 해 조인트의 각도와 액츄에이터의 토크를 기반으로 하는 방 법, 모터의 전류, 전압 등을 이용하여 외부 힘을 예측하는 방법 이 있었다^[10,11]. 이렇게 진행되었던 연구들은 로봇의 다이나믹 모델이나 모터의 전류 정보에 의존한다. 그러므로 모델이나 전류의 부정확성은 힘 예측 오차의 원인이 된다. 이러한 제한 을 극복하고자 정확한 다이나믹 모델을 만들어 외부 힘을 예측 하고자 하는 연구가 진행되었다^[12]. TDE (Time delay estimation) 를 기반으로 외부 힘을 예측하는 연구가 진행되었다. 비선형 의 다이나믹은 연속적이거나 부분 연속적이고 시간 지연은 충 분히 작다고 가정하였다. 즉 짧은 측정 시간 동안 로봇이 동일 한 다이나믹 시스템을 가진다는 것이다. 이 때 관절 토크 센서 를 통해 외부 힘을 예측하였다. 또한 불확실성에 성능이 결정 되는 것을 극복하기 위해 EKF (Extend Kalman Filter)를 사용 하는 연구가 진행되었다^[13]. 관절 토크 센서를 사용하는 과정 에서 측정되는 토크 정보가 노이즈 및 진동이 발생하기 때문 에 이를 부드러운 결과 및 외부 힘 예측을 하기 위해 RLS (Recursive least-square)를 사용하였다^[14,15].

본 연구에서는 다 관절 로봇의 조인트 토크 센서를 통해 엔 드이펙터에 가해지는 힘에 대한 정보를 예측하는 알고리즘을 제안하고 이를 실험을 통해 검증하였다. 기존의 RLS가 충격 에 의한 반응이 일어났을 때 충격 전의 정보와 합쳐서 수렴시 키기 때문에 빠르게 반응하지 못한 것을 보완하는 Modified RLS를 힘 예측 알고리즘으로 제안하였다. 외부의 힘이 엔드 이펙터에 가해지면 각 관절에서는 외부 힘에 의한 토크가 발 생하며 이 때 별도의 알고리즘을 통하여 외부 힘을 예측하게 된다. 제안 된 알고리즘은 개발된 6 축 로봇 실험에 적용하여 입증하였다. 검증된 방법을 통해 실제 산업현장에서 사용되는 Peg-in-Hole 작업에 적용하여 그 실용성을 확인하였다.

2. 로봇 하드웨어 및 토크 센서 구성

2.1 로봇 하드웨어

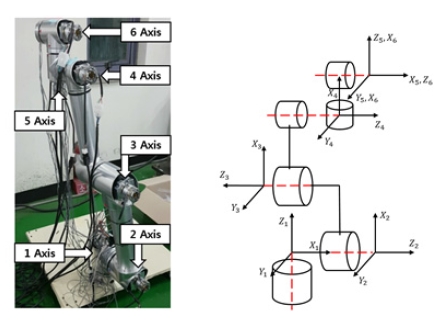
로봇의 하드웨어는 Universal robot의 외형을 기반으로 개 발되었다. 회전식 6축 다 관절 로봇으로 1, 2, 3축 조인트 모듈 과 4, 5, 6축의 조인트 모듈, 링크 파트로 크게 나누어져 있다. 힘이 상대적으로 많이 걸리는 하단 축과 적게 걸리는 상단부 의 모터 용량을 다르게 하여 로봇 전체의 무게를 줄일 수 있도 록 하였다. 각 조인트 모듈은 모터, 모터 드라이버, 하모닉 드 라이브, 알루미늄 재질 프레임으로 구성되어 있다. 하모닉 드 라이브를 통해 조인트 모듈이 높은 위치 정확도, 토크 출력, 비 틀림 강성을 얻을 수 있도록 하였다. [Fig. 1]은 로봇의 결합된 사진, 좌표계 시스템을 보여준다. 좌표계 시스템은 [Table 1]의 D-H parameter를 기반으로 결정된다.

Fig. 1

Picture of the developed robot and the scheme of coordinate systems

Table 1

D-H parameter of robot

2.2 토크 센서

스트레인 게이지를 사용하는 토크 센서를 구성하였다. [Fig. 2]와 같이 제작된 토크 센서는 아웃 프레임, 이너 프레임, 스포크, 구멍이 있는 스포크로 구성되어 있다. [Fig. 3] (a)의 A 는 구멍이 있는 스포크이며 양쪽 측면에 4개의 스트레인 게이 지가 [Fig. 3] (b)과 같이 부착된다.

Fig. 2

Detailed picture of torque sensor; (a) the main frame and the connecting plate, (b) the stain gauge attached to the spoke with slit, (c) the combined torque sensor

Fig. 3

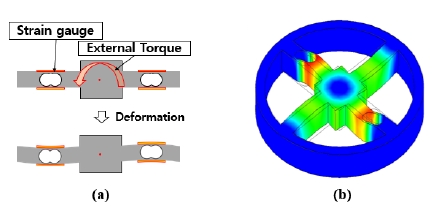
(a) Schematic picture of elastic spokes deformation, (b) the simulation result of deformation by external torque

스포크의 변형이 많이 일어나는 것은 스트레인 게이지를 통한 토크 센서의 측정을 용이하게 하지만 토크 센서가 관절 의 사이에 설치되기 때문에 로봇의 제어 성능을 저하시키는 원인이 된다. 이를 해결하기 위해 토크 센서의 스포크 중 스트 레인 게이지를 부착할 구멍이 있는 스포크를 두 개만 구성하 여 로봇의 제어 성능의 저하를 최소화하고 변형률 측정에 용 이하도록 설계하였다^[16-18].

토크가 발생을 하면 [Fig. 3] (a)과 같이 탄성 스포크가 부착 된 스트레인 게이지가 변형을 하게 되며 변형된 스트레인 게 이지는 저항이 변하게 된다. 4개의 변하는 저항에 대해 휘트스 톤 브릿지를 구성하여 전압을 얻는다. 얻어진 전압은 증폭, 필 터 과정을 거쳐 컴퓨터에서 토크 데이터로 얻어진다. 본 실험 에서는 ADC로 HX711 칩을 사용하였다.

3. 외부 힘 예측 모델

3.3 외부 힘 예측 : Modified recursive least square

Van et al.는 RLS를 기반으로 외부 힘 예측 알고리즘을 2 DOF 로봇 시스템에 적용하여 시뮬레이션을 진행하였다^[21]. 2 개의 토크 센서를 통해 2차원 평면상의 외부 힘 F_x, F_y 성분에 대한 예측을 진행하였으며 이 때 센서를 계측하여 정보를 얻 는데 걸리는 시간은 1 ms이었다. 식 (9)의 λ=0.99로 셋팅하고 100개씩 정보를 저장하고 결과를 산출하였다. 이 때 실질적으 로 노이즈가 줄어든 결과를 얻을 수 있었지만 실제 힘에 수렴 하는데 100 ms의 딜레이가 발생하게 되었다.

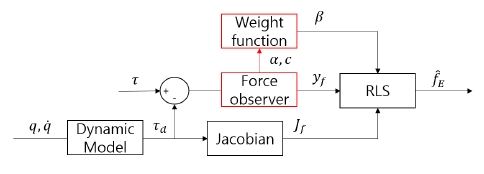
외부 힘이 발생하였을 때 외부힘이 발생하였음을 판단하는 Force observer를 구성하였다. 힘 관측기에서 외부 힘을 감지하 게 되면 새로 들어온 정보에 가중치를 주는 Modified weright function 을 생성하였다. 이렇게 변화된 시스템은 [Fig. 4]의 블 록다이어그램에 나타난 것과 같다. 식 (9)의 가중치 함수에 의 해 힘이 발생하였다는 변수 α와 다시 안정화 된 상태의 가중 치 함수로 돌아갈 수 있는 카운트 c를 정하였다.

Fig. 4

Modified weight function when t = 50

(14)

$\[ {}_{c=c+1}^{\alpha =1}\text{ifc}\ne \text{t} \]$

(15)

$\[ \begin{array}{ll}\begin{array}{l}\alpha =1\hfill \\ c=1\hfill \end{array}\hfill & \text{if}\hspace{0.17em}\left|y_i-y_{i-1}\right|\ge {\tau }_{threshold}\hfill \end{array} \]$

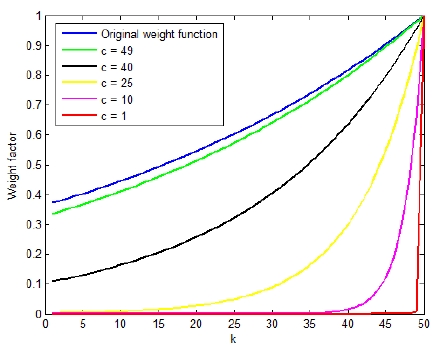
두 변수를 포함한 가중치 함수는 식 (14)와 같다. 이 때 변수 α, c는 식 (15)의 관계를 따른다. y_i가 외부 힘에 의한 레지듀 얼 토크라고 할 때 힘 관측기에 의해 이전 정보에 대한 레지듀 얼 토크가 증가하여 역치값보다 커지게 되면 충돌을 인지하게 된다. 이 때 카운트 c는 1이 되며 계산 과정마다 1씩 증가하게 된다. 이 때 카운트의 증가에 따라 이전의 값들에게도 추천된 값만큼의 가중치가 가해지며 안정화된 결과를 얻을 수 있게 된다. 카운트 증가에 따른 Modified weight function의 가중치 는 [Fig. 5]와 같다.

Fig. 5

Modified weight function when t = 50

4. 실험 및 결과

4.1 Modified recursive least square 검증

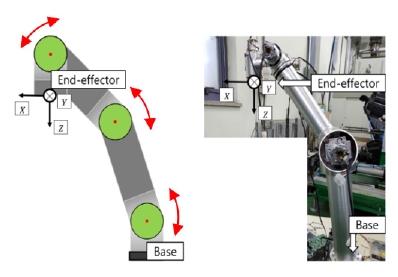
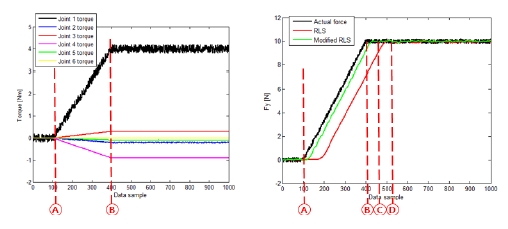
알고리즘을 검증하기 위해 [Fig. 6]과 같은 로봇의 각 축 링 크 포지션을 q₁ = [0°, 10°, 30°, 50°, -90°, 0°] 으로 위치시키고 $$ f_E=\left[f_{Ex},\hspace{0.17em}{f}_{Ey},\hspace{0.17em}{f}_{Ez},\hspace{0.17em}{m}_{Ex},\hspace{0.17em}{m}_{Ey},\hspace{0.17em}{m}_{Ez}\right]=\left[0\hspace{0.17em}N,\hspace{0.17em}9.81\hspace{0.17em}N,\hspace{0.17em}0\hspace{0.17em}N,\hspace{0.17em}0\hspace{0.17em}Nm,\hspace{0.17em}0\hspace{0.17em}Nm,\hspace{0.17em}0\hspace{0.17em}Nm\right]$$의 힘을 가하는 실험을 진행하였다.

Fig. 6

ConFiguration of the robot and coordinate of the end-effector

[Fig. 7]은 실험의 결과 그래프이다. 1 sample은 1 ms와 동일 하다. Reference논문과의 비교 편의를 위해 sample 단위를 사 용하였다. 좌측은 힘이 가해졌을 때 각 축의 토크 센서에서 측 정되는 값과 계산된 값을 뺀 레지듀얼 토크 값이다. 우측은 실 제 힘과 RLS, Modified RLS의 결과를 나타낸 그래프이다. A ~ B는 힘이 가해지는 시간이다. B ~ C, B ~ D는 각각 Modified RLS와 RLS 방법이 실제 힘에 수렴하는데 걸리는 시간을 나타 낸 것이다. 시스템에서 하드웨어의 스펙에 따라 계측에 걸리 는 시간이 달라지므로 몇 개의 정보가 들어 왔다는 의미의 sample 단위를 사용하였다. RLS의 경우 113 samples 뒤에서 실제 힘에 수렴하였으며 Modified RLS를 통해서는 51 samples 후에 실제 힘에 수렴하였다. 가중치 함수의 변경을 통해 실제 힘에 수렴하는데 걸리는 시간을 54.9% 감소시킬 수 있었다.

Fig. 7

Residual torque data and estimated external force when applying y-direction force at end-effector

4.2 외부 힘 예측 실험

[Fig. 6]은 로봇의 동작 상태를 나타낸다. 기본적으로 실험 에서 로봇은 2^nd, 3^rd, 4^th 축을 0 ~ 50°를 반복 동작을 하며 힘이 가해졌을 때 원점으로 회귀하는 동작을 수행하였다.

정적 상태는 원하는 방향, 크기로 직접적으로 힘을 가할 수 있지만 동적 상태에서는 이 부분이 불가능하기 때문에 [Fig. 8] 과 같이 힘을 계측할 수 있는 장비를 구성하였다. 힘의 방향을 측정하기 위해 자이로 센서를 사용하였고 힘의 크기를 측정하 기 위해 로드셀 장비를 사용하였다. 이를 하나의 모듈로 만들 어 엔드이펙터 끝 단에 위치 할 수 있도록 하였다. 힘을 가하는 모듈을 [Fig. 9]와 같이 여러 방향에서 힘을 가하며 실험을 진 행하였다.

Fig. 8

Force measuring device at end-effector

Fig. 9

Picture of various external force direction

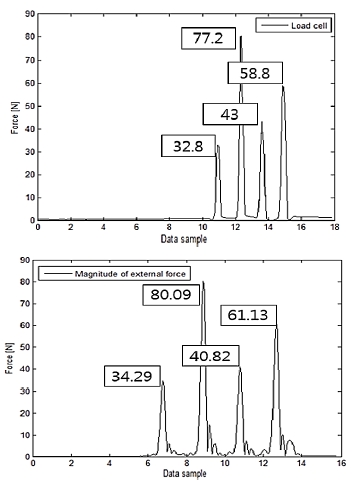
[Fig. 10]은 엔드이펙터에 힘이 가해졌을 때 얻어진 여유 토 크와 Modified RLS을 통해 예측된 외부 힘 $$ {\widehat{f}}_E$$의 성분 $$ {\widehat{f}}_{Ex}$$, $$ {\widehat{f}}_{Ey}$$, $$ {\widehat{f}}_{Ez}$$를 나타낸 그래프이다. 각 그래프에서 여유 토크가 크 게 증가하는 부분은 힘 측정 장비에 힘을 가한 순간이다. 로봇 의 끝 단을 손으로 잡고 미는 동작을 행하였기 때문에 여유 토 크 부분이 크게 증가, 감소하고 나서 적은 진동이 발생하는 것 을 확인 할 수 있다.

Fig. 10

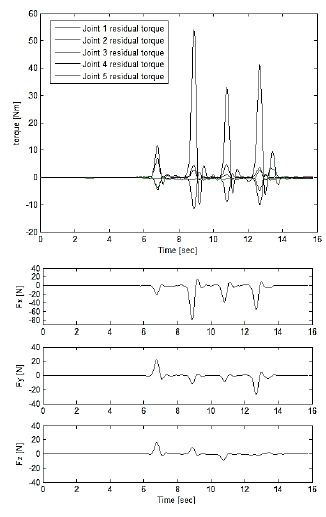
Experimental results of external force estimation experiment; residual torque and estimated external force

[Fig. 11]은 예측된 외부 힘의 크기와 로드셀로부터 측정된 외부 힘의 크기이다.

Fig. 11

Amplitude of the actual force measured from loadcell

힘의 크기의 경우 [Fig. 11]의 그래프에서 최대 지점을 찍는 지점의 크기로 비교를 하였다. 이를 통하여 예측된 힘의 크기 가 실제 힘에 대해 얼마나 차이가 나는지를 확인하였다. 해당 실험에서 두 센서의 샘플링 레이트에 차이가 있었기 때문에 샘플의 수로 표기하였다.

[Table 2]와 [Table 3]은 엔드이펙터에 가해진 외부 힘 예측 실험의 결과에 대한 오차율과 사잇각을 나타낸 표이다. Solt et al. 의 논문과 Van et al.의 논문에서는 3축 로봇을 기준으로 이 론을 실험과 시뮬레이션을 통해 검증하였다^[8,21]. Solt의 논문 을 참고하였을 때 외부 힘 예측 알고리즘이 유의미한 결과를 갖는 것을 보여주고 있다.

Table 2

Average force magnitude of each case

Table 3

Average included angle between actual external force vector and estimated force vector

4.3 펙인홀 작업

실제 산업현장에서 많이 사용되는 펙인홀 작업에 적용하기 위한 절차를 세우고 실험을 진행하였다. 기본적인 홀의 위치 가 지정된 상태에서 삽입을 진행할 때 외부 힘에 대한 반응이 발생하면 삽입 위치를 수정하여 다시 삽입을 진행한다. 구멍 의 위치를 찾고 삽입을 진행 할 때 재밍이 감지되면 펙의 삽입 각도를 수정하며 진행을 한다.

[Fig. 12]의 좌측 사진은 실험 장비 셋팅 사진으로 펙의 경우 에는 로봇의 엔드이펙터 끝 단에 직접적으로 부착하여 6 번 축 의 회전축과 일치하도록 하였다. 구멍은 알루미늄 프레임에 부착을 하여 고정시켰다.

Fig. 12

Picture and schematic picture of experimental setup

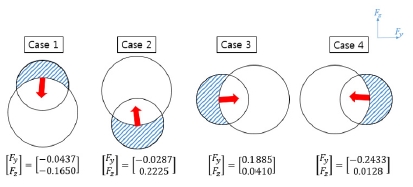
[Fig. 12]의 우측은 펙인홀 작업의 개략도로 기본적으로 구 멍의 위치를 알고 있는 상태에서 구멍과 축의 비틀어짐 없이 삽입을 진행하도록 구성하였다. 이 때 로봇이 구멍의 근처에 서 충돌했을 경우 구멍의 위치를 갱신하기 위한 과정이 필요 하다. 외부 힘 예측 알고리즘을 통해 펙을 구멍 근처에 충돌을 하였을 때 예측되는 외부 힘에 대해 확인하였다. 구멍의 상하 좌우에 대해 실험을 진행하였며 상하좌우를 각각 Case 1~4로 정하였다.

이 때 [Table 4]는 각 Case의 반복 실험에 따른 예측된 외부 힘 유닛 벡터 성분을 표현한 것이다. [Fig. 13]은 F_y, F_z성분을 벡터로 표현한 것이며 이를 통해 삽입 위치를 수정할 수 있음 을 확인하였다.

Table 4

Estimated external force at hole position check process

Fig. 13

Fx and Fy of estimated external force at hole position check process

[Fig. 14]는 펙인홀 작업을 수행한 일련의 사진으로 처음에 는 정확한 구멍 위치에 존재하지 않고 약간 틀어진 곳에서 삽 입을 진행한다. 충돌을 감지하고 위치를 수정한 후 마지막에 는 끝까지 삽입을 성공 한 것을 확인 할 수 있다.

Fig. 14

A series of pictures of peg-in-hole task

5. 결 론

본 논문에서는 관절 토크 센서에서 얻어지는 정보를 토대 로 하여 엔드이펙터에 가해지는 힘에 대한 정보를 예측하는 방법에 대해 제안하였다. 관절 토크 센서에서 측정되는 값과 로봇의 다이나믹 모델을 통해 외부 힘에 대한 여유 토크 성분 을 얻을 수 있었다. 여유 토크와 기하학적 정보를 통해 Modified RLS로 외부 힘에 대해 예측 할 수 있었다.

펙인홀 작업 어플리케이션에 적용하기 위해 로봇의 동작을 구현해가며 외부 힘 예측 실험을 진행하였다. 실제로 가한 외 부 힘과 예측한 외부힘의 크기 오차는 모든 경우에 대해 최소 2.81%, 최대 5.34%, 평균은 4.11%로 나타났다. 또한 실제로 가 한 외부 힘 벡터와 예측한 외부 힘 벡터 사이각도는 최소 3.59°, 최대 7.83°이며 평균은 5.04°이었다. Solt의 논문을 참고하였 을 때 외부 힘 예측 알고리즘이 유의미한 결과를 갖는 것을 보 여주고 있다^[8,21].

6축 로봇의 엔드이펙터에 가해지는 외부 힘에 대한 활용을 위해 펙인홀 작업을 수행하였다. 펙인홀 작업을 수행하기 위 해서 필요한 홀을 찾는 작업과 재밍을 방지하며 삽입하는 과 정이 있다. 예측되는 힘을 기반으로 홀의 위치를 찾아 삽입을 완료하는 과정까지 수행할 수 있었다.

본 연구결과를 통해 각 축에 설치된 관절 토크 센서와 Modified RLS 통해 6축 로봇의 엔드이펙터에 가해진 외부 힘 을 예측에 대해 검증하였다. 기존의 방법에 비해 빠르고 정확 하게 가해진 외부 힘에 대해 예측 할 수 있었다. 이를 통해 펙인 홀 어플리케이션 전략을 수립하고 유용성을 검증하였다.

References

• J.B. Beak, J.U. Jeong, S.U. Son, The case study on robot gripper for gripping force control robot gripper, KSPE Spring Conference, Jeju, Korea, p435-436, (2015).
• M.T. Mason, Compliance and force control for computer controlled manipulators., IEEE Trans. Syst. Man Cybern., (1981), 11(6), p418-432. [https://doi.org/10.1109/tsmc.1981.4308708]
• T. Tsuji, A. Jazidie, M. Kaneko, Multi-point impedance control for redundant manipulators., IEEE Trans. Syst. Man Cybern. B Cybern., (1996), 26(5), p707-718. [https://doi.org/10.1109/3477.537313]
• C.H. Park, J.H. Kyung, D.I. Park, K.T. Park, D.H. Kim, D.G. Gweon, Direct teaching algorithm for a manipulator in a constraint condition using the teaching force shaping method., Adv. Robot., (2010), 24(8-9), p1365-1384. [https://doi.org/10.1163/016918610x501471]
• P.W. Jeon, Implementation and control of crack tracking robot using force control: Part II. Force Control., Journal of Institute of Control, Robotics and Systems, (2005), 11(4), p337-343.
• Springer Handbook of Robotics, B. Siciliano, K. Oussama, Berlin, Heidelberg, Springer, (2008).
• O. Kerpa, K. Weiss, H. Worn, Development of a flexible tactile sensor system for a humanoid robot, 2003 IEEE/RSJ International Conference on Intelligent Robots and Systems, Las Vegas, NV, USA, (2003). [https://doi.org/10.1109/iros.2003.1250596]
• A. Stolt, M. Linderoth, A. Robertsson, R. Johansson, Force controlled robotic assembly without a force sensor, 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, (2012). [https://doi.org/10.1109/icra.2012.6224837]
• S. Lu, J.H. Chung, S.A. Velinsky, Human-robot collision detection and identification based on wrist and base force/torque sensors, 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, (2005).
• P.J. Hacksel, S.E. Salcudean, Estimation of environment forces and rigid-body velocities using observers, 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, (1994). [https://doi.org/10.1109/robot.1994.351233]
• N. Prajumkhaiy, Sensorless force estimation of SCARA robot system with friction compensation., Procedia Comput. Sci., (2016), 86, p120-123. [https://doi.org/10.1016/j.procs.2016.05.030]
• M. Jin, S.H. Kang, P.H. Chang, Robust compliant motion control of robot with nonlinear friction using time-delay estimation., IEEE Trans. Ind. Electron., (2008), 55(1), p258-269. [https://doi.org/10.1109/tie.2007.906132]
• J. Jung, J. Lee, K. Huh, Robust contact force estimation for robot manipulators in three-dimensional space., Proc. Inst. Mech. Eng., C J. Mech. Eng. Sci., (2006), 220(9), p1317-1327. [https://doi.org/10.1243/09544062c09005]
• A. Stolt, M. Linderoth, A. Robertsson, R. Johansson, Force controlled robotic assembly without a force sensor, 2012 IEEE International Conference on Robotics and Automation, Saint Paul, MN, USA, (2012). [https://doi.org/10.1109/icra.2012.6224837]
• Y.-J. Park, W.-K. Chung, Exact external torque sensing system for flexible-joint robot: kalman filter estimation with random-walk model, The Journal of Korea Robotics ciety, (2014), 9(1), p11-19. [https://doi.org/10.7746/jkros.2014.9.1.011]
• D. Tsetserukou, R. Tadakuma, H. Kajimoto, S. Tachi, Optical torque sensors for implementation of local impedance control of the arm of humanoid robot, 2006 IEEE International Conference on Robotics and Automation, Orlando, FL, USA, (2006). [https://doi.org/10.1109/robot.2006.1641947]
• J-K. Min, H-S. Yu, K-H. Ahn, J-B. Song, Robot joint module equipped with joint torque sensor with disk-type coupling for torque error reduction, International Conference on Intelligent Robotics and Applications, Springer, Cham, p371-378, (2015). [https://doi.org/10.1007/978-3-319-22879-2_34]
• J-K. Min, H-S. Kim, J-B. Song, Joint module with joint torque sensor having disk-type coupling for torque error reduction., Transactions of the Korean Society of Mechanical Engineers A, (2016), 40(2), p133-138. [https://doi.org/10.3795/ksme-a.2016.40.2.133]
• M.W. Spong, Modeling and control of elastic joint robots., J. Dyn. Syst. Meas. Control, (1987), 109(4), p310-318. [https://doi.org/10.1115/1.3143860]
• L Ljung, System identification, Signal Analysis and Prediction, (1998), Birkhäuser, Boston, MA.
• M. Van Damme, P. Beyl, B. Vanderborght, V. Grosu, R. Van Ham, I. Vanderniepen, A. Matthys, D. Lefeber, Estimating robot end-effector force from noisy actuator torque measurements, 2011 IEEE International Conference on Robotics and Automation, Shanghai, China, (2011). [https://doi.org/10.1109/icra.2011.5980210]