접촉 압력 분포를 이용한 로봇 의료 촉진

1. 서 론

촉감 정보(tactile information)를 이용한 촉진(palpation) 은 종괴(lump)의 진단이나 수술 전 혹은 수술 중 종괴의 위치를 특정하는 데 있어 유용한 정보를 제공한다. 현재 이러한 촉진은 시술자의 손에 의해서, 혹은 수술 중 수술 도구를 통하여 간접적으로 이루어진다. 하지만 현재의 촉진은 진단 결과가 시술자의 숙련도에 의존적이며^[1] 로 봇을 이용한 최소 침습 수술(robotic minimally invasive surgery; RMIS)과의 병행이 힘들다는 한계가 있다^[2].

이러한 한계점의 극복하기 위해 제안된 것이 Fig. 1과 같은 로봇이 수행 또는 보조하는 촉진의 완전 혹은 부분 적 자동화이며, 최근 이에 관한 연구가 활발히 진행되어 왔다^[3-8]. 이러한 연구들은 강성 매핑(stiffness mapping)을 기반으로 하여 촉진을 수행하는 접근 방법을 취해왔다.

Fig. 1

An example of robotic palpation system

Talasaz와 Patel^[3]은 원격 조작(teleoperation)으로 제 어되는 촉각 센서(tactile sensor)가 부착된 매니퓰레이터 를 사용하여 접촉 압력 분포(contact pressure distribution) 와 변형을 측정하여 이를 기반으로 강성 매핑을 수행하였 다. Beccani 등의 연구^[4,5]에서는 압력 센서와 자기장을 이 용하여 접촉 시의 압력과 변형을 각각 측정하여 얻은 강성 매핑을 통하여 종괴의 탐지를 수행했다. Wanninayake 등 의 연구^[6,7]에서는 공압(air pressure)과 광섬유 등을 활용 하여 임의의 표면에서의 힘과 변형을 측정하는 장비를 개발, 이를 이용한 강성 매핑을 수행하였다. Nichols와 Okamura^[8]는 6축 힘 센서와 3자유도의 매니퓰레이터를 이용하여 전체 영역의 선행 촉진으로 낮은 분해능의 강성 매핑을 수행하여 종괴의 위치를 대략적으로 추정한 후 그 주변에서 세밀하게 촉진을 수행하여 종괴의 위치, 영 역 및 그 모양을 추정하였다.

이러한 강성 맵 기반의 접근 방법들은 종괴의 기하 구조를 파악하기 어렵다는 한계를 지니고 있다. 따라서 강성 맵을 바탕으로 종괴의 정확한 모양 추정을 위해서 는 Nichols의 결과^[8]에서 보듯 종괴와 그 주변 위치에 대하여 많은 데이터를 필요로 한다.

본 연구에서는 이러한 문제를 개선하기 위하여 접촉 압력 분포를 이용한 새로운 로봇 촉진 방법을 제안한다. 제안하는 방법은 접촉 압력 분포로부터 Kim 등의 연구^[9] 를 기반으로 한다. Kim의 연구에서는 접촉 압력 분포로 부터 접촉면의 법선 벡터(surface normal)와 수직력(normal force)을 구하고 이들의 방향의 차이를 이용하여 종괴의 감지를 수행하였다. 본 연구에서는 이를 확장하여 종괴 의 기하학적인 정보를 실시간으로 추정하며 이를 이용 하여 종괴의 모양을 추정하는데 필요한 최적의 촉진 경 로를 실시간으로 계산, 이를 따라서 최적화된 촉진을 수 행한다.

제안하는 방법의 가장 큰 강점은 촉진 경로가 실시간 으로 종괴의 모양을 추종하는 형태로 생성된다는 점이 다. 종괴의 모양의 정밀한 추정을 위해 종괴의 예상 위치 주변에 대하여 많은 횟수의 촉진이 수행되어야 하는 강 성 맵 기반의 접근 방법과 달리, 제안하는 방법은 촉진 그 자체를 종괴의 모양을 따라서 수행할 수 있다. 따라서 촉진 경로로부터 바로 종괴의 모양을 추정할 수 있다. 이는 훨씬 짧은 시간 및 적은 데이터로 정밀한 종괴의 모양 추정을 가능하게 한다.

이후의 구성은 다음과 같다. 2절에서는 접촉 압력으로 부터 종괴의 경계면 추종을 위한 경계면의 법선 및 접선 벡터의 계산과 이를 바탕으로 촉진 경로를 생성하는 방 법에 대하여 설명한다. 3절에서는 센서의 형상이나 센서 신호의 노이즈의 영향을 줄이기 위한 방법에 대하여 기 술하고, 4절에서 제안한 방법을 실제로 적용하여 그 성 능을 실험적으로 검증하며 5절에서 결론 및 의의에 대하 여 논한다.

2. 접촉 압력을 이용한 종괴 경계면 추종

본 절에서는 촉각 센서로부터 얻은 접촉 압력 분포로 부터 종괴의 법선 벡터를 도출하는 방법에 대해 기술한 다. Kim이 제시했던 방법^[9]을 기반으로 이를 3차원으로 확장하여 현재 촉진 중인 표면의 접평면을 기준으로 한 종괴의 법선 벡터를 도출한다. 본 방법에서 가정하는 촉 진 환경은 다음과 같다. 1) 촉진을 수행하는 로봇의 엔드 이펙터에는 볼록(convex)한 형상의 촉각 센서가 장착되 어 있고, 2) 종괴가 존재하는 영역의 영의 계수(Young’s modulus)는 다른 영역의 영의 계수보다 크다.

2.1. 종괴 법선 추정

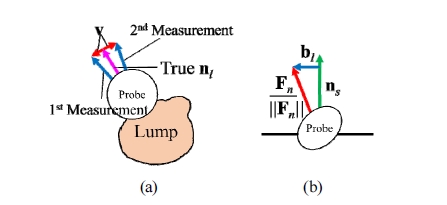
Kim의 연구^[9]에서 언급하였듯이, 균일한 물성을 지니 는 탄성체(elastic body)와 대칭을 이루는 강체(rigid body) 간의 접촉에서는 접촉 압력의 분포가 Fig. 2(a)와 같이 대칭을 이룬다. 이 때에는 접촉면의 법선 벡터와 수직력의 방향이 서로 일치한다. 하지만 탄성체 안에 종 괴가 존재하고 그 경계면 부근에서 접촉이 이루어질 경 우 접촉 압력 분포가 Fig. 2(b)와 같이 더 이상 대칭이 아니게 된다. 이 때에는 접촉면의 법선 벡터와 수직력의 방향에 차이가 발생하게 된다. 이를 통하여 종괴의 경계 면의 위치를 도출할 수 있다.

Fig. 2

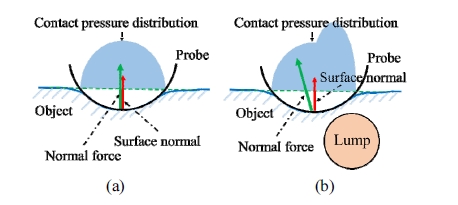
(a) Symmetric contact pressure distribution in the contact between the probe and homogeneous object and (b) asymmetric contact pressure distribution in the contact between the probe and heterogeneous object with a lump

종괴의 경계면의 위치 계산에 필요한 수직력 F_n 과 접 촉면의 법선 벡터 n_s 는 촉각 센서를 이용해 측정한 접촉 압력 분포로부터 다음과 같이 구할 수 있다. M1M2M3

$\[ {\mathbf{\text{F}}}_n=-{\displaystyle \sum _{i=1}^n{\rho }_i{\mathbf{\text{n}}}_i{A}_i,} \]$

(1)

$\[ \text{n}\prime s=-{\displaystyle \sum }_{i=1}^{n}1({\rho }_i){\text{n}}_i{A}_i, \]$

(2)

$\[ {\mathbf{\text{n}}}_s=\frac{{{\mathbf{\text{n}}}^{\prime }}_S}{\Vert {{\mathbf{\text{n}}}^{\prime }}_S\Vert }. \]$

(3)

여기서 1(ρ_i) 는 다음과 같다.M4

$\[ 1\left({\rho }_i\right)=\{\begin{array}{ll}1,\hfill & if{\rho }_i>{\rho }_{th}\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}. \]$

(4)

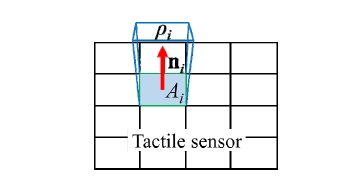
여기서 ρ_i , n_i , A_i 는 각각 i 번째 촉각 정보의 측정된 접촉 압력, 해당 압력에 대응되는 법선 벡터와 접촉 면적 이다(Fig. 3). ρ_th는 접촉 유무의 판단을 위한 임계값 (threshold)이며, 촉각 센서의 부하가 걸리지 않은 조건 하에서의 노이즈에 따라 설정되는 값이다.

Fig. 3

Data of an element of the tactile sensor array

계산된 n_F 의 방향 $$ {\text{F}}_n/\Vert {\text{F}}_n\Vert $$ 과 n_s 의 차이 e_l을 다음과 같이 구할 수 있다.M5

$\[ {\mathbf{\text{e}}}_l=\frac{{\mathbf{\text{F}}}_n}{\Vert {\mathbf{\text{F}}}_n\Vert }-{\mathbf{\text{n}}}_s, \]$

(5)

두 단위 벡터(unit vector)의 차이인 e_l은 그 특성상 Fig. 4(a)와 같이 n_s에 수직이 아닌 방향을 가지고 있다. 촉진 수행에 필요한 법선 정보는 e_l 중 n_s 에 수직한 방향 의 성분이므로, 다음과 같이 n_s 에 수직한 종괴 경계면의 법선 벡터 n_l을 구한다.M6

Fig. 4

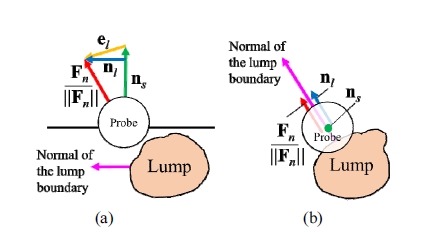
Errors between the normal force direction and surface normal at the boundary of the lump, (a) side view and (b) top view

$\[ {\mathbf{\text{n}}}_l={\mathbf{\text{e}}}_l-\left({\mathbf{\text{e}}}_l\cdot {\mathbf{\text{n}}}_s\right){\mathbf{\text{n}}}_s. \]$

(6)

n_l 은 촉진을 수행한 위치가 종괴의 경계면일 때 그 크기가 커지게 된다. 따라서 다음의 식이 성립할 때 해당 위치를 종괴의 경계면으로 추정할 수 있다.

$\[ \Vert {\text{n}}_l\Vert >L_{th}. \]$

(7)

이 때 n_l의 방향은 Fig. 4와 같이 항상 종괴의 경계면 의 법선 방향이 된다. 따라서 n_l의 방향을 구하는 것으 로 종괴의 경계면의 법선 벡터를 구할 수 있다.

2.2. 촉진 경로 생성

본 소절에서는 이전 소절에서 얻은 종괴의 법선 정보 로부터 종괴의 외곽을 추종하는 촉진 경로를 생성하는 방법에 대하여 기술한다. 이전 및 현재의 촉진 위치 p 및 n_l로부터 현재 위치의 종괴 경계면의 곡률 반경 (radius of curvature)을 구하고 이와 종괴 경계면의 접선 벡터(tangent vector)로부터 다음 촉진 지점을 계산한다.

n_s 및 n_l로부터 종괴 표면의 접선 벡터 t_l 을 다음과 같이 구할 수 있다.

$\[ {\mathbf{\text{t}}}_l={\mathbf{\text{n}}}_s\times \frac{{\mathbf{\text{n}}}_l}{\Vert {\mathbf{\text{n}}}_l\Vert }. \]$

(8)

가장 간단한 경로 생성 방법으로는 식 (8)에서 구한 t_l 의 방향을 따라가는 것이다. 하지만 이산화(discretize) 된 경로를 추종하는 촉진 과정 상 현 지점의 t_l 방향 만을 추종하는 촉진 경로로는 종괴의 경계를 감싸지 못 하고 Fig. 5(a)와 같이 그 경계를 벗어나게 된다. 이러한 문제를 줄이기 위해 다음 촉진 지점을 t_l 와 일치하는 직선 상의 위치가 아닌 Fig. 5(b)와 같이 현재 촉진 위치 에서 t_l 과 접하고 그 위치에서의 종괴 경계면의 곡률 반경만큼의 반지름을 가지는 원호 상의 위치가 되도록 다음 촉진 위치를 계산하였다.

Fig. 5

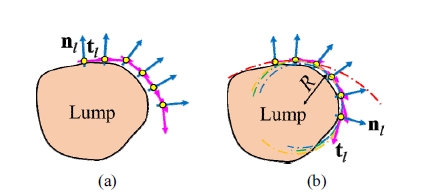
(a) Trajectory generation via tangent vector and (b) trajectory generation via both tangent vector and radius of curvature

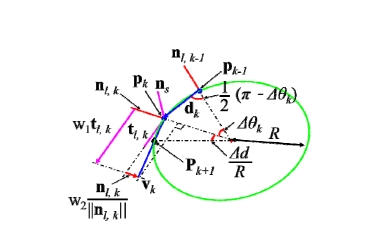
종괴 경계면의 곡률 반경 R 은 다음과 같이 구할 수 있다. 우선 다음과 같이 k − 1 번째 촉진 위치 p_k−1부터 k 번째 촉진 위치 p_k 까지의 벡터 d_k 및 p_k−1 에서 계산 된 종괴의 법선 n_{l, k - 1} 와 p_k에서 계산된 법선 벡터 n_{l, k} 사이의 각도 Δθ_k 를 구한다.M9

$\[ {\mathbf{\text{d}}}_k={\mathbf{\text{p}}}_k-{\mathbf{\text{p}}}_{k-1}, \]$

(9)

$\[ \Delta {\theta }_k=\text{sgn}\left({\mathbf{\text{d}}}_k\cdot {\mathbf{\text{t}}}_{l,k}\right){\text{cos}}^{-1}\left(\frac{{\mathbf{\text{n}}}_{l,k-1}\cdot {\mathbf{\text{n}}}_{l,k}}{\Vert {\mathbf{\text{n}}}_{l,k-1}\Vert \Vert {\mathbf{\text{n}}}_{l,k}\Vert }\right). \]$

(10)

식 (10)에서 $$ \text{sgn}\left({\text{d}}_k\cdot {\text{t}}_{l,k}\right)$$ 는 n_s 를 기준으로 반시계 방 향일 경우 양수, 시계 방향일 경우 음수가 된다. 이 때 p_k-1 과 p_k사이의 R에 대응되는 원의 중심과 p_k−1과 pk 는 Fig. 6과 같이 이등변 삼각형을 이루며, 사인 법칙 을 이용하여 R 을 다음과 같이 도출할 수 있다.M11M12

Fig. 6

Derivation of radius of curvature and determination of pk+1

$\[ C=\text{sgn}\left(\left({\mathbf{\text{n}}}_{l,k-1}\times {\mathbf{\text{n}}}_{l,k}\right)\cdot {\mathbf{\text{n}}}_s\right), \]$

(11)

$\[ R=C\frac{\Vert {\mathbf{\text{d}}}_k\Vert }{\text{sin\hspace{0.17em}}\Delta \theta }\text{sin}\left(\frac{1}{2}\left(\pi -\Delta \theta \right)\right). \]$

(12)

여기서 C 는 n_{l, k − 1} 와 n_{l, k} 를 기준으로 볼록한 곡면일 경우 양수, 오목한 곡면일 경우 음수가 된다.

촉진을 일정한 간격 Δd만큼 움직이면서 수행하고 움 직이는 방향을 v_k라 할 때 다음 촉진 수행 위치는 다음 과 같이 구할 수 있다.

$\[ {\mathbf{\text{p}}}_{k+1}={\mathbf{\text{p}}}_k+\Delta d{\mathbf{\text{v}}}_k \]$

(13)

이 때 Fig. 5(b)와 같이 계산된 곡률 반경 R 에 의한 궤적을 추종하기 위해서는 Fig. 6과 같이 식 (13)의 p_k+1 이 R 에 대응되는 원호 상에 위치해야 한다. 이 조건을 만족시킬 수 있는 v_k는 다음과 같이 t_{l, k} 와 n_{l, k} 의 선형 조합(linear combination)으로 구할 수 있다.M14

$\[ {\mathbf{\text{v}}}_k=w_1{\mathbf{\text{t}}}_{1,k}+w_2\frac{{\mathbf{\text{n}}}_{1,k}}{\Vert {\mathbf{\text{n}}}_{1,k}\Vert }, \]$

(14)

$\[ w_1=\text{sgn}\left({\mathbf{\text{d}}}_k\cdot {\mathbf{\text{t}}}_{l,k}\right)\text{sgn}\left(\frac{\Delta d}{R}\right), \]$

(15)

$\[ w_w=\text{sgn}\left({\mathbf{\text{d}}}_k\cdot {\mathbf{\text{t}}}_{l,k}\right)C\left(\text{cos}\left(\frac{\Delta d}{R}\right)-1\right). \]$

(16)

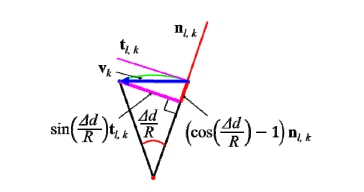
식 (15)의 sin(Δd/R)와 식 (16)의 cos(Δd/R)−1는 Fig. 7과 같이 식 (13)의 Δdv_k 가 원호 상에 있어야 한다는 구속 조건으로부터 도출되는 t_l,k 와 n_l,k 방향 각각의 비율이며, $$ \text{sgn}\left({\text{d}}_k\cdot {\text{t}}_{l,k}\right)$$ 와 C 는 상술 하였듯이 이동 방 향과 원호의 볼록 혹은 오목 함에 의해 결정되는 부호이다.

Fig. 7

Determination of vk via linear combination of tl, k and nl, k

Δd의 값에 따라서 촉진의 종괴의 경계면 추종 성능과 시간적 효율성은 등가교환(trade-off)의 관계를 가진다. Δd를 작은 값으로 설정하면 종괴의 경계면을 더 정확하 게 얻을 수 있지만 촉진 시간이 증가한다. 반면 Δd를 큰 값으로 설정하면 촉진 시간이 감소하는 반면 종괴 경계면의 정확성이 감소하거나 너무 큰 값일 경우 종괴 경계면의 추종에 실패할 수 있다.

3. 노이즈 보정

본 절에서는 센서의 형상이나 노이즈 등에 의한 편향 (bias) 및 비 편향(unbiased) 오차를 줄이는 방법에 대하 여 설명한다.

3.1. 노이즈의 종류

본 연구에서 제안하는 방법은 종괴가 존재하지 않는 영역에서 측정된 F_n과 n_s 의 방향이 완전히 일치하는 것을 전제로 하고있다. 하지만 이는 촉각 센서의 형상이 완벽한 구형을 이루고 또한 센서의 노이즈가 없다는 가 정 하에서만 성립한다. 실제 환경에서는 여러 요인 때문 에 이러한 조건을 충족시키는 것이 어렵기 때문에 종괴 가 존재하지 않는 영역에서도 측정한 F_n과 n_s 의 방향 에 약간의 오차가 존재하며, 이 오차는 비편향 오차 (unbiased error) 및 편향 오차(biased error)를 모두 포함 하고 있다.

비편향 오차는 촉각 센서의 각각의 압력 측정 요소들 이 가지는 측정 오차로 인하여 발생한다. Fig. 8(a)와 같 은 비편향 오차는 계산된 n_l의 크기와 방향이 안정적으 로 계산되는 것을 막아 생성된 경로가 안정적으로 종괴 의 경계면을 추종하는 것을 방해한다.

Fig. 8

(a) Unbiased error v and (b) biased error bl during the palpation.

편향 오차는 센서의 형상의 비대칭성이나 분해능의 한계, 모서리 부분과의 접촉 등에 의해 발생한다. 편향 오차가 0이 아닐 경우 Fig. 8(b)와 같이 종괴가 없는 영역 에서도 $$ \Vert {\widehat{n}}_l\Vert >0$$ 인 $$ {\widehat{n}}_l={\text{b}}_l$$ 이 항상 존재하게 된다. 이로 인해 종괴의 경계면에서 계산되는 $$ {\widehat{n}}_l$$ 또한 다음과 같이 참 값과 편향 오차 b_l의 합으로 나타나게 된다.M17

$\[ {\widehat{\mathbf{\text{n}}}}_l={\mathbf{\text{n}}}_l+{\mathbf{\text{b}}}_l \]$

(17)

이는 n_l이 b_l과 같은 방향일 경우 $$ \Vert {\widehat{\mathbf{\text{n}}}}_l\Vert $$ 이 참값보다 큰 값을 가지게 하며, 반대 방향일 경우 $$ \Vert {\widehat{\mathbf{\text{n}}}}_l\Vert $$ 이 참값보다 작은 값을 가지게 한다. 이로 인해 특정 방향(− b_l)과 비 슷한 방향의 종괴의 검출 및 경계면 추종 성능이 저하될 수 있다.

3.3. 노이즈 감소 방법을 포함한 로봇 촉진 과정

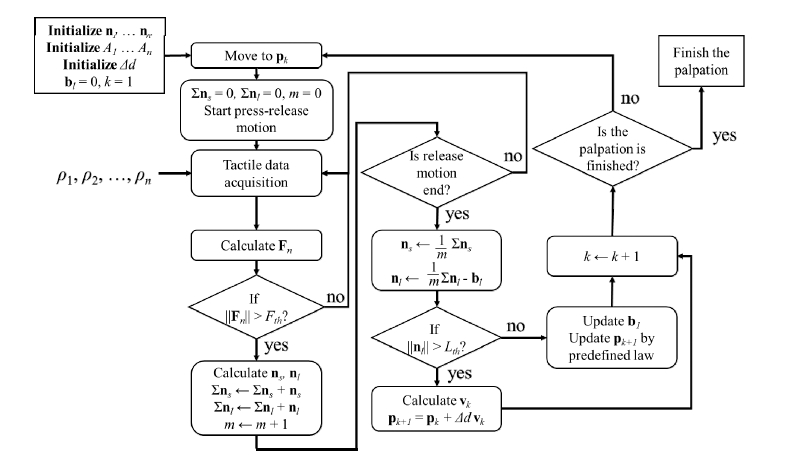
이러한 노이즈 감소 과정을 포함한 한 위치에서의 촉 진 과정을 도식화하면 Fig. 9와 같다. 우선 k 번째 촉진 위치 p_k로 이동한 후 누름 동작을 시작한다. 해당 동작 을 수행하는 동안 매 순간 측정하는 접촉 압력 $$ {\rho }_1,{\rho }_2,\cdots ,{\rho }_n$$ 로부터 F_n을 구한다. F_n의 크기가 미리 설 정된 임계값 F_th 보다 큰 경우에만 n_s 및 n_l을 구하고 이를 저장한다. 누름 및 복귀 동작이 수행되는 동안 매 순간 얻어지는 접촉 압력에 대하여 이 과정을 반복한다.

Fig. 9

Flowchart of the entire palpation process

복귀 동작까지 모두 완료한 후 쌓인 각각 m개의 n_s 및 n_l 값으로부터 이들의 평균을 구한다. 이 때 n_l의 평균 값은 그 값을 구한 후 bias error b_l을 빼서 보정한 다. 만약 식 (7)이 성립하면 계산된 n_s 및 nl의 평균 값으로부터 식 (8)-(16)을 이용하여 n_s 및 p_k+1 을 구한 다. 만약 식 (7)이 성립하지 않으면 계산된 n_l의 평균 값과 식 (18)을 이용하여 b_l을 갱신한다. p_k+1는 미리 설정한 종괴가 없을 때의 촉진 면을 훑는 경로를 따라가 도록 설정해준다.

이후 로봇은 p_k+1 지점으로 이동하며 다시 위의 동작 을 반복한다. 이러한 과정을 미리 설정된 종료 조건을 만족할 때까지 반복하는 것으로 촉진을 수행한다.

4. 실 험

본 절에서는 제시한 촉진 방법의 종괴의 경계면 추종 성능을 실험적으로 검증한다. 전체적인 실험 환경은 Fig. 1과 같다. 접촉 압력 정보의 측정이 가능한 매니퓰레이 터를 이용하여 정상 조직 및 종괴를 모사한 모형의 촉진 을 수행했다. 촉진에 사용한 매니퓰레이터는 6자유도를 가지는 뉴로메카의 Indy-RF이며, Pressure profile system 사의 DigiTact-Custom 촉각 센서를 사용하여 접촉 압력 의 측정을 수행했다. 촉각 센서는 4×6개의 접촉 압력 값의 분포를 측정한다. 측정한 접촉 압력 분포는 20×30 의 크기로 선형 보간(linear interpolation)을 이용한 업샘 플링(upsampling)을 수행한 후 10×10의 크기를 가지고 표준편차가 3인 가우시안 필터(Gaussian filter)를 적용 한 뒤 ρ_th 이상의 압력 값만을 취하였다. 원본 및 필터 적용 후의 접촉 압력 데이터 및 이에 대응하는 법선 벡터 n_i 및 면적 A_i 는 Fig. 10과 같다.

Fig. 10

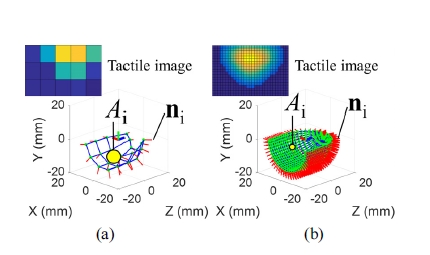
Tactile sensor data and its corresponding ni and Ai of (a) the original sensor configuration and (b) interpolated configuration

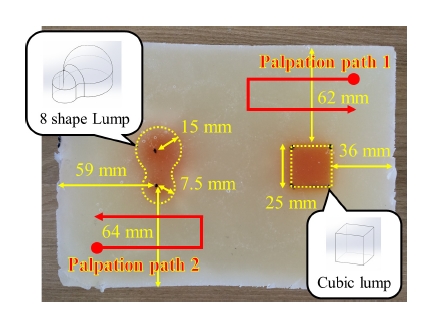
실험에 사용한 조직 모형은 Fig. 11과 같다. 이 모형의 전체 크기는 150 mm × 200 mm × 47 mm이며, 각 변이 25 mm인 정육면체 모양의 종괴와 각 부분의 직경이 각 각 15 mm, 7.5 mm 인 8자 모양의 종괴가 삽입되었다. 각 종괴 표면의 최고점과 전체 모형의 표면 사이의 거리 는 약 4-5 mm이다. Nichols의 연구^[8]에서 사용된 조건과 동일하게 M-F Manufacturing에서 판매하는 plastisol을 사용, 정상 조직을 모사한 부분은 plastisol과 플라스틱 유연제를 1.75:1로 섞은 재질을, 종괴를 모사한 부분은 plastisol 만을 사용하여 제작하였다.

Fig. 11

Used tissue phantom during the experiment

실험은 매니퓰레이터의 엔드이펙터를 촉진 시작 지점 에 위치시킨 후 접촉 압력 정보에 기반하여 다음 촉진을 수행할 위치를 결정한 후 다음 위치로 이동하여 촉진을 반복적으로 수행하는 방식으로 진행하였다. 종괴의 경 계면이 아닌 영역으로 판단되었을 경우 모형을 오른쪽 에서부터 왼쪽으로 이동하면서 상/하로 번갈아가면서 스캔하는 위치로 다음 촉진 위치를 결정하였다. 이 때 이전 위치와의 간격은 15 mm가 되도록 하였다. 종괴의 경계면으로 판단되었을 경우 제안한 방법을 이용하여 다음 촉진 위치를 결정하도록 하였다. 이 때의 촉진 간격 Δd는 4 mm로 설정하였다. L_th , F_th 는 각각 0.035와 0.75 N으로 설정하였다. 매니퓰레이터가 모형의 스캔을 모두 완료하거나 종괴의 경계면 추종을 완료한 뒤 처음 종괴의 경계면을 탐지한 위치로 돌아왔을 때 전체 촉진 과정이 완료되도록 했다. 실험은 총 10회 수행하였으며, 5회는 Fig. 11의 촉진 경로 1 (palpation path 1)의 경로를 따라서 정육면체 모양의 종괴의 탐지를, 5회는 촉진 경 로 2 (palpation path 2)의 경로를 따라서 8자 모양의 종괴 의 탐지를 수행하였다.

촉진 성능의 정량적인 비교를 위해 Nichols의 연구^[8] 에서 사용한 민감도(sensitivity)와 특정도(specificity)를 차용하여 사용하였다. 민감도와 특정도를 계산하기 위 한 면적은 Fig. 12와 같이 도출하고 이를 다음의 식에 대입하여 민감도와 특정도를 구하였다.

Fig. 12

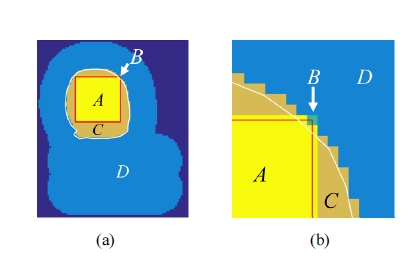
An example of segmented sections via palpation, (a) entire view and (b) magnified view. The area covered by red lines is the true lump and the area covered by white curves is the estimated lump. A: true positive, B: false negative, C: false positive, and D: true negative

식 (19)-(20)의 A, B, C, D는 Fig. 12에 표기된 동 기호 에 해당하는 영역의 면적이다.

전체 실험 에서 구한 민감도와 특정도의 값은 Table 1과 같다. 총 10 회의 촉진 결과에 대한 민감도의 평균은 0.9966, 표준편차는 0.006092였으며 특정도의 값의 평균 은 0.9211, 표준편차는 0.03326이었다. 정육면체 모양의 종괴를 사용한 실험들의 민감도 및 특정도는 각각 0.9997±0.000716, 0.8944±0.02540이었으며 8자 모양의 종괴를 사용한 실험들의 민감도와 특정도 값은 각각 0.9936±0.007759, 0.94778±0.007942였다. 이 결과를 Nichols 의 결과^[8](민감도 0.875-0.983, 특정도 0.879- 0.948)와 비교하였을 때 제시한 방법이 종괴의 영역을 충분히 정 확하게 구별해낼 수 있음을 말해준다.

Table 1

Sensitivity and specificity

Fig. 13은 10회의 실험 중 4회의 실험 결과를 나타낸 다. 각 실험 결과에서 종괴의 경계면 추종을 수행한 경로 (파란 선)가 실제 종괴의 경계면(붉은 선)의 대부분을 감싸고 있는 것을 볼 수 있다. 또한 Fig. 14에서 보듯 종괴 주변과 그 이외의 영역에서의 $$ \Vert {\widehat{\mathbf{\text{n}}}}_l\Vert $$ 값이 확연히 차 이가 나는 것을 볼 수 있다.

Fig. 13

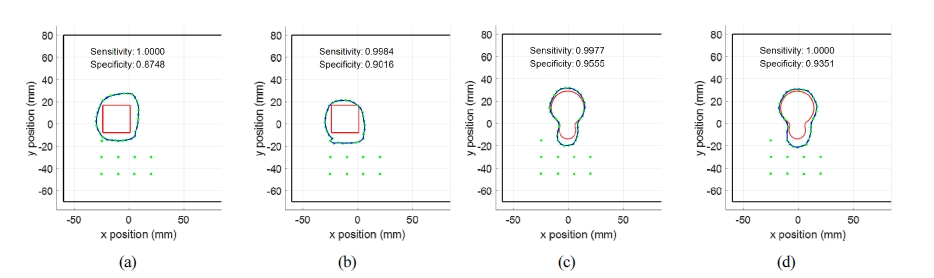
Palpation trajectory plots (top view) of 4 selected results, true position of the lump (red line), the actual position of the palpation samples (greed dot), and the estimated boundary of the lump (blue line)

Fig. 14

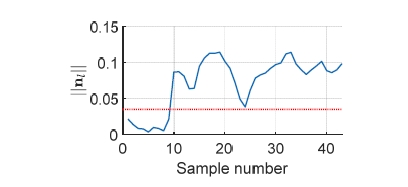
‖nl‖ plot from the result of Fig. 15(a). Lth is represented by red dotted line. The samples after the sample number 10 are the samples where the lump boundary tracking was activated

또한 일반적인 강성 매핑에 기반한 종괴 검출 방법과 비교했을 때 종괴의 구별을 위해 필요한 촉진 횟수가 확연히 적은 것을 볼 수 있다. Nichols의 연구^[8]에서는 종괴의 크기 및 모양의 식별을 위해 모든 면적에 넓은 간격의 촉진을 우선 수행하고, 그 후 종괴로 추정되는 영역의 안쪽 및 주변부에 대한 조밀한 촉진을 추가로 수행해야 했다. 하지만 제시한 방법은 종괴의 경계면의 실시간 추정을 가능해 본 실험 결과와 같이 훨씬 적은 촉진 횟수 만으로 정확한 종괴의 구분을 가능하게 한다. 이는 전체 촉진 과정에서 가장 긴 시간을 필요로 하는 실제 촉진 동작을 수행하는데 필요한 시간을 획기적으 로 줄임으로써 빠른 촉진을 가능하게 한다.

5. 결 론

본 연구에서는 로봇 촉진 방법의 정확성 및 속도를 높일 수 있는 촉각 센서 정보를 활용한 새로운 로봇 촉진 방법을 제시하였다. 촉각 센서의 정보를 바탕으로 추정 할 수 있는 접촉 면의 법선 벡터와 수직력의 특성을 기반 으로 실시간으로 종괴 경계면의 위치 및 해당 면의 법선 벡터의 추정을 수행했다. 이를 이용하여 훨씬 적은 데이 터로부터 정확한 종괴 영역의 추정이 가능한 촉진 경로 를 실시간으로 생성하였다. 정육면체 및 8자 모양의 종 괴 모형을 사용한 실험에서 기존의 결과와 비교했을 때 제시한 방법의 결과가 전반적으로 높은 민감도와 비슷 한 특정도를 가지는 것을 확인하였다. 이는 제시한 방법 이 종괴 모양에 상관 없이 종괴 영역의 구분을 기존의 방법보다 정확하게 수행할 수 있음을 보여준다. 또한 실 험에서 필요한 촉진의 시행 횟수가 기존의 방법 대비 훨씬 적은 것을 확인하였다. 이는 제시한 방법이 촉진 수행 시간 또한 획기적으로 줄일 수 있어 신속한 촉진의 수행을 가능하게 함을 보여준다. 이러한 결과를 바탕으 로 본 연구에서 제시하는 방법이 보다 빠르고 정확한 로봇 촉진을 가능하게 할 것으로 기대한다.

Acknowledgments

This work was supported in part by the Engineering Research Center (No. 2011-0030075), the Global Frontier R&D Program (No. 2012M3A6A30564 23), and the Mid-Career Researcher Grant (No. NRF-2013R1A2A2A010 16907) funded by the NRF of Korea and by the Industrial Technology Innovation Program (No. 10048358) funded by the Ministry of Trade, Industry, & Energy of Korea.

References

• Harris, R., Kinsinger, L.S., Routinely teaching breast selfexamination is dead. What does this mean?, J. Natl. Cancer Inst, (2002), 94(19), p1420-1421. [https://doi.org/10.1093/jnci/94.19.1420]
• Ottermo, M.V., Vstedal, M., Lang, T., Stavdahl, Y., Yavuz, T. Johansen, and R. Marvik, “The role of tactile feedback in laparoscopic surgery, Surg. Laparo. Endo. Per, (2006), 16(6), p390-400. [https://doi.org/]
• Talasaz, A., Patel, R.V., Telerobotic palpation for tumor localization with depth estimation, (2013), Proc. of IEEE/RSJ IROS 2013, Tokyo, Japan. [https://doi.org/10.1109/iros.2013.6696392]
• Beccani, M., Natali, C.D., Rentschler, M.E., Valdastri, P., Wireless tissue palpation: proof of concept for a single degree of freedom, Proc. of IEEE ICRA 2013, Karlsruhe, Germany, p711-717, (2013). [https://doi.org/10.1109/icra.2013.6630651]
• Beccani, M., Natali, C.D., Sliker, L.J., Schoen, J.A., Rentschler, M.E., Valdastri, P., Wireless tissuepalpation for intraoperative detection of lumps in the soft tissue, IEEE Trans. Biomed. Eng, (2014), 61(2), p353-361. [https://doi.org/10.1109/tbme.2013.2279337]
• Wanninayake, I.B., Seneviratne, L.D., Althoefer, K., Novel indentation depth measuring system for stiffnesscharacterization in soft tissue palpation, (2012), Proc. of IEEE ICRA 2012, Minnesota, USA. [https://doi.org/10.1109/icra.2012.6225127]
• Wanninayake, I.B., Seneviratne, L.D., Althoefer, K., Estimation of tissue stiffness using a prototype of air-float stiffness probe, Proc. of IEEE ICRA 2014, Hong Kong, China, p1426-1431, (2014). [https://doi.org/10.1109/icra.2014.6907039]
• Nichols, K.A., Okamura, A.M., Methods to segment hard inclusions in soft tissue during autonomous robotic palpation, IEEE Trans. Robot, (2015), 31(2), p344-354. [https://doi.org/10.1109/tro.2015.2402531]
• Kim, H., Choi, S., Chung, W.K., Feasibility of a novel indicator for lump detection using contact pressure distribution, (2015), Proc. of IEEE/RSJ IROS 2015, Hamburg, Germany. [https://doi.org/10.1109/iros.2015.7353658]
• Kim, H., Choi, S., Chung, W.K., Contact force decomposition using contact pressure distribution, IEEE RA-L, (2017), 2(1), p290-297. [https://doi.org/10.1109/lra.2016.2598554]