근력 지원용 외골격 로봇을 위한 수동형 무릎 관절 메커니즘 개발

1. 서 론

산업과 군사현장에서는 중량물 이송, 절단툴 등을 이 용한 작업 등의 고 하중 지지를 요구하는 작업들이 많다. 가령, 절단 툴을 사용하여 작업하거나 중량물을 이송할 때 작업자는 중량물의 하중을 지지하며 작업을 수행하 게 된다. 최근 이러한 작업들의 근력지원을 위한 외골격 로봇이 개발되고 있다. 그 중 하지 외골격 로봇은 인체의 하지 골격과 유사하게 구성되어 평지, 경사 등 다양한 지형에서 근력지원이 가능하도록 개발된다. 특히, 로봇 의 관절 구동 장치는 중량물의 하중을 지면에 전달되도 록 하여 착용자에게 그 하중이 가해지지 않도록 개발된 다. 미국의 Raytheon 사는 ‘XOS Exoskeleton’ 로봇을 개발하였다^[1]. 이 로봇은 유압장치가 구성되어 있으며, 미사일, 탄약등의 고 하중을 지면으로 전달하여 착용자 의 근력지원 및 작업능력을 향상시켰다. 한국의 한양대 학교에서는 ‘HEXAR’를 개발하였다^[2]. 이 로봇은 전기 모터와 하모닉드라이브 기어로 구성되며, 재난 현장과 산업 현장에서 착용자의 근력지원이 가능하도록 개발되 었다.

앞서 소개된 외골격 로봇을 다양한 환경에서 운용하 기 위해 각 관절마다 고가의 엑츄에이터가 사용되고 제 어를 위한 고가의 센서들이 부착된다. 하지만 이러한 로 봇은 비용적으로 비효율적이라는 문제가 제기되고 있으 며, 한정된 베터리 용량 대비 고출력 엑츄에이터를 사용 하여 장시간 사용이 불가능하게 된다. 최근, 이러한 효율 성 문제를 해결하기 위해 특정 작업을 위한 외골격 로봇 이 개발되고 있다. 이러한 외골격 로봇은 장시간 근력지 원을 위하여 엑츄에이터 수를 줄이거나 없애고 링크구 조 형태나 스프링, 댐퍼 등 기계적 요소를 적용하여 개발 되고 있다. 네덜란드의 TU Delf 에서는 인공 tendon을 적용한 수동형(passive) 외골격 로봇인 ‘XPED’를 개발 하였다^[3]. 이 로봇은 보행 시 인체의 근육 특성과 비슷한 스프링 구조를 개발하여 착용자가 보행시 근육의 에너 지 사용량을 최소화할 수 있도록 하였다. 미국의 MIT 대학에서는 준수동(quasi-passive) 외골격 로봇을 개발하 였다^[4]. 이 로봇은 고 관절에 캠 메커니즘과 스프링, 무릎 관절에는 가변댐퍼, 발목 관절에는 스프링 카본을 적용 하였고, 평지보행에서 중량물의 하중이 지면에 전달되 도록 하여 착용자의 근력지원이 가능하도록 하였다. 미 국의 Lockheed Martin 사는 고하중의 툴을 지탱하여 착 용자의 근력을 지원하는 외골격 로봇인 ‘FORTIS’를 개 발하였다^[5]. 이 로봇은 고관절에 균형(counter balance)장 치를 고안하여 작업자가 기립자세에서 장시간 절삭작업 을 할 수 있도록 개발되었다. 이러한 외골격 로봇들은 특정 작업목표를 선정하여 근력지원이 가능하도록 인체 관절의 운동학적, 역학적 해석을 통한 메커니즘 설계 개 발에 초점을 두었다.

본 연구에서는 고하중의 툴을 이용한 작업과 이송작 업에 대해 근력 지원이 가능한 무릎관절 메커니즘을 개 발하고자 하였다. 특히 기립 자세와 보행 시 엑츄에이터 를 사용하지 않고 메커니즘 설계만으로 하중을 지면에 전달되도록 하였고, 인체의 무릎관절과 운동학적으로 유사하게 설계하여 착용자와의 이질감을 줄이고자 하였 다. 본 연구를 위해 고관절과 발목관절은 근력지원이 가 능한 메커니즘 또는 엑츄에이터가 설계되어 있다고 가 정하였다.

2. 무릎 메커니즘 설계

2.1. 무릎 관절 특성 분석

외골격 로봇은 인체관절의 가동범위(range of motion, ROM)와 회전력(torque) 등의 데이터를 기준으로 설계되 며, 설계 구상 시 가장 중요한 요소가 된다^[6]. 본 절에서 는 고하중에 대한 무릎의 근력지원이 가능하며 관절의 움직임과 유사하게 동작하는 메커니즘을 개발하기 위해 발이 지면에 닿아 몸의 하중을 지탱하는 구간인 입각기 (stance)와 발이 지면에 떨어져 전진을 위해 다음 지면까 지 이동하는 구간인 유각기(swing)에 대한 무릎 관절의 역학적, 운동학적 특성을 분석하였다.

2.1.1. 무릎의 역학적 특성

외골격 로봇의 근력지원은 중량물의 하중을 지면에 전달시키는 개념이므로 하중지지가 이루어지는 입각기 구간에 대해 무릎의 역학적 특성을 분석하였다. 이 구간 에서의 각 관절은 몸의 하중을 다리로 지지하며 인체 무게중심을 앞으로 이동시키기 위해 관절 회전력을 생 성한다. 이러한 동적인 움직임에서의 하중지지를 위한 회전력은 보행의 동적 안정성(dynamic stability)을 확보 하며^[7], 무릎 관절은 동적 안정성 확보를 위해 지면과 발 사이에 발생하는 지면 반발력 벡터(ground reaction force vector, GRFV)와 관절 회전점의 상대적 위치에 따 라 회전력을 생성한다.

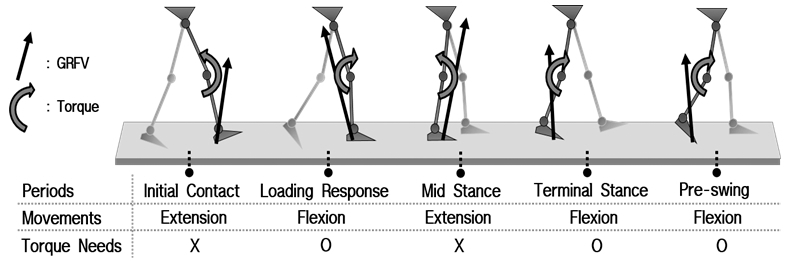
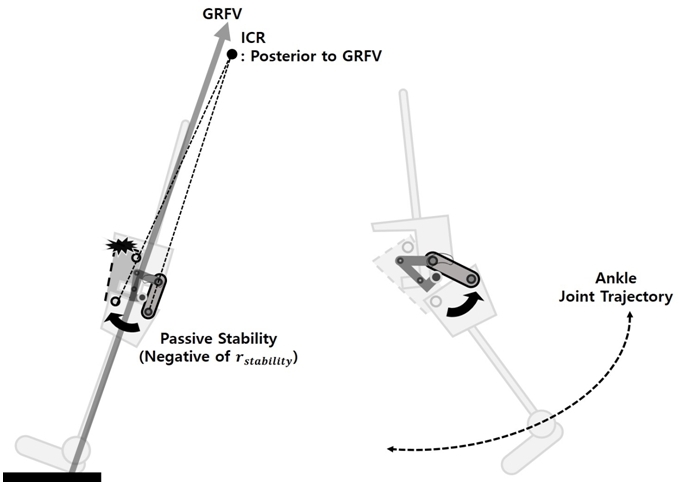
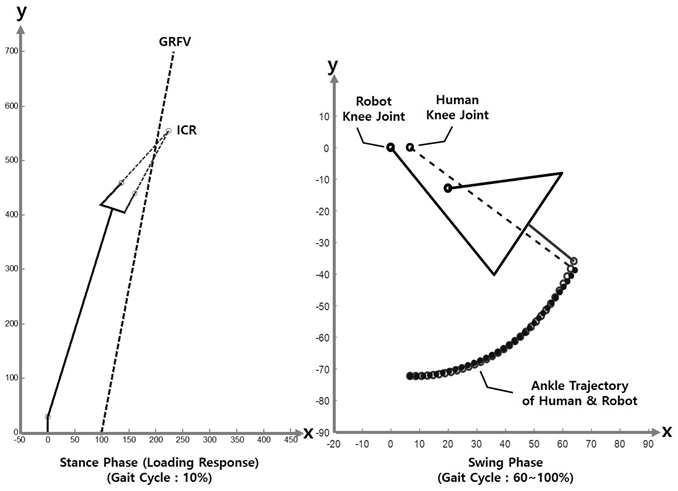
무릎의 동적 안정성은 Fig. 1과 같이 5가지의 구간에 서 특성을 보인다. 초기 발과 지면과의 접촉구간인 초기 접지기(initial contact)에서의 무릎은 지면 반발력 벡터 가 무릎관절 앞에 위치하게 되며, 무릎을 신전(extension) 시키는 대퇴사두근(quadricept)에 의한것이 아닌 지면 반 발력에 의한 수동적 신근 회전력으로 신전하여 동적 안 정성을 확보한다. 보행주기의 0~10% 구간인 체중부하 기(loading Response)에서는 지면 반발력 벡터가 무릎 관절 뒤에 위치하게 되어 굴곡(flexion)이 일어나게 되며, 동적 안정성 확보를 위해 대퇴사두근의 편심성 수축으 로 신전방향의 회전력을 생성한다. 보행주기의 10~30% 구간인 중간입각기(mid stance)에서는 지면반발력 벡터 가 관절 회전점의 뒤에서 앞으로 넘어오는 시기이며 신 전방향 회전력 발생으로 동적 안정성이 확보된다. 보행 주기의 30~50% 구간인 말기입각기(terminal stance)와 50~60% 구간인 초기유각기(pre-swing)에서는 지면 반 발력 벡터가 관절 회전점의 앞에서 뒤로 이동하며 반대 편 다리로 무게 이동이 일어나 작은 회전력으로 굴곡하 게 된다.

Fig. 1

Knee Joint Torque Versus GRFV

이처럼 지면 반발력 벡터와 무릎 회전점의 상대적인 위치는 보행의 동적 안정성과 관계가 있으며, 벡터의 위 치가 회전점 앞에 위치하게 되면 수동적 신근 회전력으 로 신전을 위한 근육 활성화 없이 동적 안정성을 확보하 게 된다.

2.1.2. 무릎의 운동학적 특성

관절 회전 시 로봇과 착용자와의 이질감을 없애며 무 릎 관절의 회전범위 조건을 만족하기 위해서는 두 관절 이 기구학적으로 유사해야하며, 이를 위해 무릎 관절의 운동학적 특성을 분석하였다.

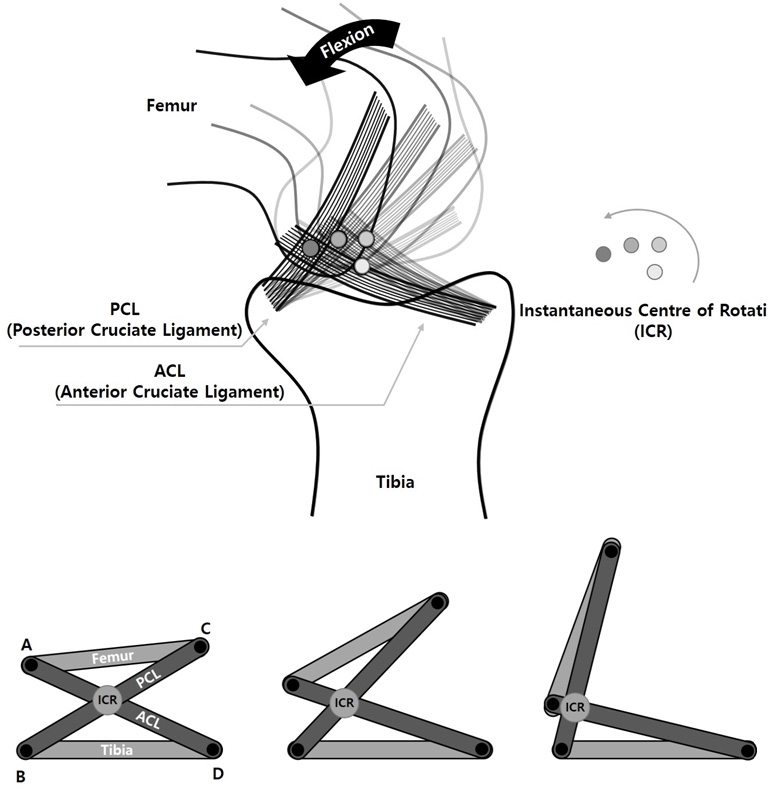
무릎의 회전중심은 Fig. 2와 같이 대퇴골과 경골이 연 결된 십자 인대의 교차점이 된다. 이러한 교차점은 무릎 회전시 원 형태의 경로를 가지게 되며, 다축(polycentric) 의 무릎 구조는 병진과 회전이 동시에 일어나는 기구학 적 특성을 보이게 된다^[8].

Fig. 2

Instantaneous Centre of Rotation & Four-bar Linkage Formed of the Knee

무릎의 관절 가동범위는 5도 정도의 신전과 160도 정 도의 굴곡으로 이루어진다. 특히, 5도 정도의 신전을 과 신전(hyperextension)이라 하며, 기립자세나 보행 시 무 릎의 회전중심이 지면 반발력 벡터 뒤에 위치하게 되면 과신전의 구조는 수동적 신근 회전력에 의해 기구적으 로 잠김(lock)이 되어 수동적 안정성(Passive Stability)을 확보할 수 있도록 한다.

2.2. 무릎 메커니즘 개념설계

2.1.2. 무릎관절 모방형 메커니즘

무릎의 동적 안정성과 다축 회전운동을 재현하기 위해 4절, 6절 등 다절 링크 구조나 다축힌지(polycentric hinge) 메커니즘이 제안되어, 하지 절단 환자를 위한 의족 이나 마비환자들을 위한 보조기 등에 적용되고 있다^[11]. 이 중 의족에 적용되고 있는 4절링크 메커니즘은 무릎의 십자인대 구조와 유사하며, Fig. 2과 같이 연결선 AC와 BD는 각각 대퇴부와 경골을 나타내고 연결선 AD와 BC 의 교차점이 회전중심점이 된다. 또한, 4절 링크 설계 시 동적 안정성을 위해 지면 반발력 벡터와 링크 회전점 의 상대적 위치가 고려되며, 인체의 무릎회전과 운동학 적 유사성을 갖는 링크 구조가 선정된다^[9,10].

의족은 보행 시 동적 안정성 확보를 위해 지면 반발력 벡터를 무릎의 회전점 앞에 위치하도록 환자의 추가적 인 고관절 회전력을 요구하며, 이 때 발생하는 링크의 신전방향 회전은 기구적인 잠김에 의해 지지 역할을 하 게 되어 하중을 지면에 전달할수 있도록 한다^[11]. 하지만 본 연구는 정상인을 위한 무릎 메커니즘으로써 추가적 인 고관절 회전력의 요구없이 지면 반발력 벡터가 무릎 회전점 앞에 위치하여 동적 안정성을 확보하여야 하며, 그와 동시에 무릎 회전 시 인체관절의 회전 움직임과의 유사성이 요구된다. 본 연구에서는 두 가지 조건을 만족 하는 메커니즘을 개발하기 위해 4절 링크의 회전중심 위치가 가변되도록 하여 입각기에서는 지면 반발력 벡 터가 링크의 회전점 앞에 위치하여 지지되고, 유각기에 서는 뒤에 위치하여 굴곡되도록 하였다. 동시에 유각기 에서 인체 무릎의 회전점과 링크의 회전점 이동이 일치 되도록 하였다.

2.2.2. 회전중심 가변형 4절 링크 메커니즘

앞서 언급한 바와 같이 입각기에서는 동적 안정성을 유지하여 착용자의 근력을 지원을 하고, 유각기에서는 굴곡 시 인체의 무릎 회전점과 일치되어 이질감을 없애 고자 하였다.

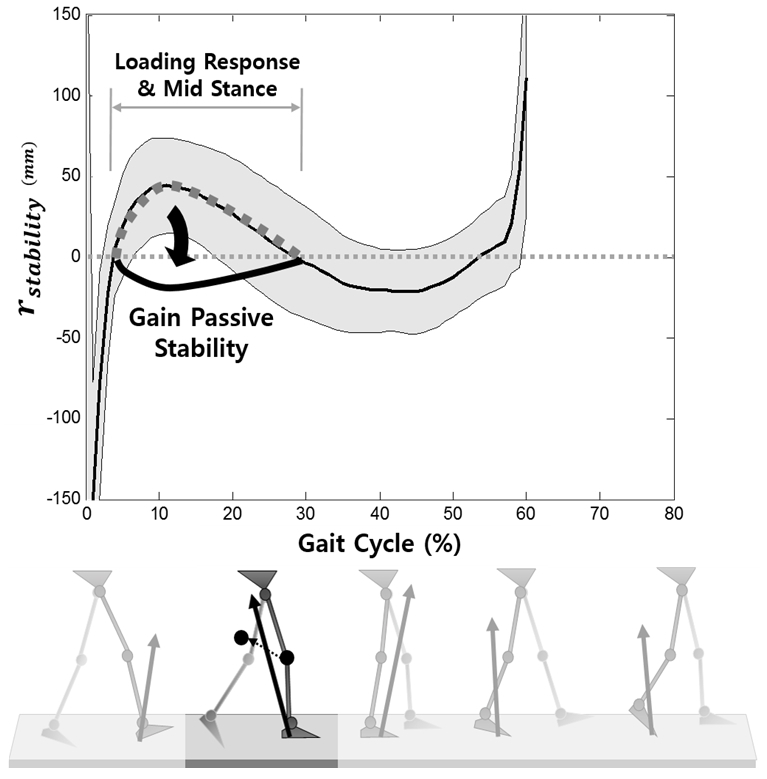
동적 안정성을 갖는 메커니즘을 설계하기 위해 보행 시 인체의 무릎 관절과 지면 반발력 벡터와의 상대적 위치 관계를 분석하였다. 관절과 벡터 사이의 상대적인 거리를 r_stability라 정의하고 식 (1)과 같이 인체 동작실험 을 통해 얻은 무릎 관절력과 지면 반발력 벡터 데이터를 이용해 거리를 구하였다. 또한 상대적 거리를 Fig. 3과 같이 입각기의 각 구간별로 도식화 하였다.

Fig. 3

Distance Between Knee Joint and GRF

$\[ r_{stability}=\frac{M_{knee}}{F_{GRF}} \]$

(1)

여기서 r_stability 값이 양수이면 벡터가 회전점 뒤에 위치 하여 굴곡이 발생하고, 인체 근육은 동적 안정성을 위해 신전방향으로 회전력을 발생시키지만 본 연구에서는 회 전력을 위한 엑츄에이터를 사용하지 않고 기구적으로 해결하고자 하였다. 그러므로 입각기 구간내의 굴곡에 의한 신전 회전력이 요구되는 체중부하기와 중간입각기 의 r_stability 값을 음수로 만들고자 하였으며, 의족과 같이 고관절의 추가 회전력에 의한 지면 반발력 벡터의 조절 이 아닌 무릎 메커니즘의 회전 중심점 위치를 이동시켜 수동적 신전 발생으로 동적 안정성을 확보하고자 하였 다. 이를 위해 회전중심의 가변기능 구현과 인체 무릎구 조와의 유사성을 갖는 4절 링크 메커니즘을 개발하였다.

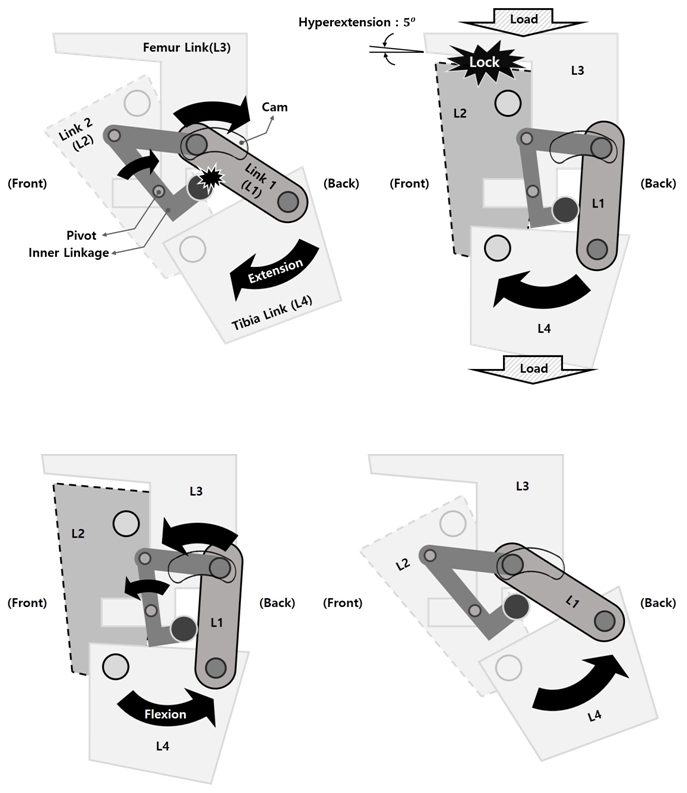
본 4절 메커니즘은 Fig. 4와 같이 두 개의 인대를 나타 내는 전방링크(L2)와 후방링크(L1)와 넓적다리부(femur) 링크(L3), 정강뼈(tibia)링크(L4)가 있으며, L3의 캠 메커 니즘과 내부 링크 메커니즘에 의해 신전 시 L1의 상위 조인트가 뒤로 이동되게 된다. 또한, 최대신전 시 L2와 L3가 접하게 되는데 5도의 각도로 무릎의 신전 각도와 유사하게 설계하였다.

Fig. 4

Knee Mechanism in Stance/Swing Phase State

본 구조는 두 가지 특성을 지니게 된다. Fig. 4의 상위 와 같이 초기 접지기 구간에서 무릎이 최대로 신전하게 되는데 내부 링크 메커니즘에 의해 L1이 뒤로 이동하여 Fig. 5의 왼쪽과 같이 의 교차점인 순간 회전 중심점이 지면 반발력 벡터 뒤로 이동되고, 5도의 과신전 각도로 인하여 초기 입각기 구간부터 수동적 신근 회전력이 생 성되어 하중이 지면에 전달될수 있도록 하는 역학적 특 성을 가지고 있다. 이는 로봇 무게중심이 반대편 다리로 이동하기 전까지 신전 방향으로 잠김 상태가 되어 하중 이 지면에 전달되도록 하였다. 무릎의 회전이 일어나는 유각기 구간에서는 Fig. 4의 하위와 같이 링크가 초기 위치로 복원되어 4절 링크의 회전 중심점은 인체의 무릎 회전 중심과 유사한 궤적을 갖게 된다. 본 구조는 입각기 가 시작되는 초기 접지기 전까지 유지되며, 실제 무릎 회전중심의 궤적을 직접 측정하기 어려우므로 본 연구 에서는 Fig. 5의 오른쪽과 같이 4절 링크 구조가 인체의 무릎 회전점을 기준으로 발목의 회전점 궤적이 일치되 도록 설계하였다.

Fig. 5

Goal of the Knee Mechanism in Stance/Swing Phase

다음 절에서는 회전 중심 가변형 4절 링크의 상세 설 계를 위해 위의 동적 안정성과 무릎 회전중심의 유사성을 위하여 최적화 설계(optimization desgin)를 진행하였다.

2.3. 무릎 메커니즘 최적화 설계

하중지지에 대한 동적 안정성 확보와 무릎 관절의 운 동학적 유사성을 위한 메커니즘 개발을 위해 최적화를 진행하였다. 이를 위해 최적화 하고자 하는 설계변수 (design variable)를 선정하고, 위의 3가지 목표를 수식화 하는 목적함수(objective function)를 수립하여 설계문제 에 대한 정식화를 통한 모든 목적함수를 만족하는 변수 값을 얻고자 하였다.

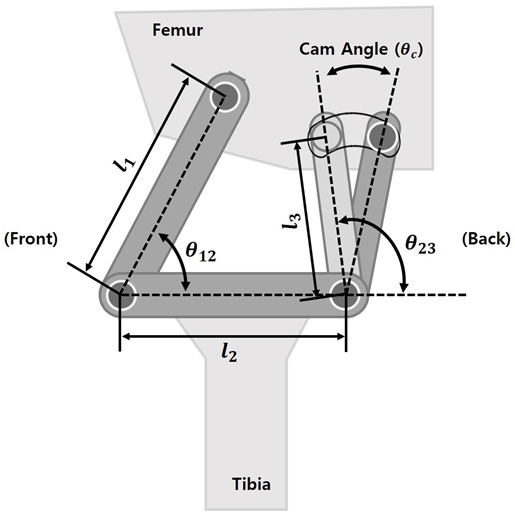
Fig. 6과 같이 무릎의 운동학적 유사성에 민감한 3개 의 링크 길이(l₁, l₂, l₃)와 초기 링크 각도 (θ₁₂, θ₂₃), 동적 안정성에 민감한 캠 각도(θ_c), 총 6개의 설계 변수를 선정 하였다.

Fig. 6

Design Variable of Novel 4-bar Linkage Mechanism

2.3.1. 동적 안정성의 목적함수

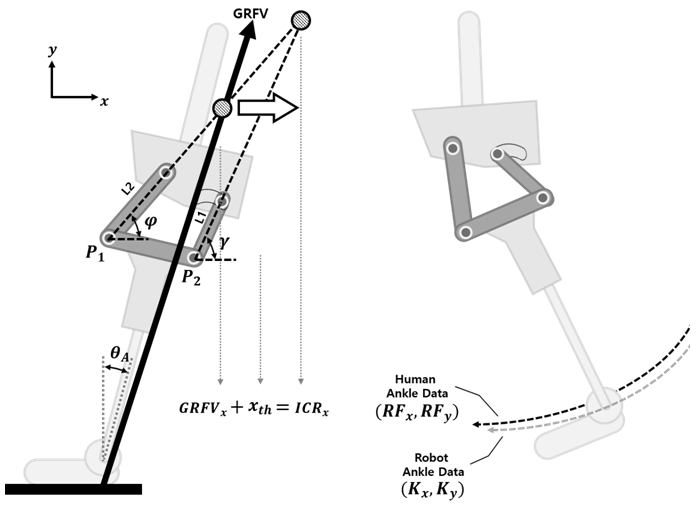
체중부하기와 중간입각기 구간에서 4절 링크 메커니 즘의 동적 안정성 확보를 위해 링크의 순간 중심점이 지면 반발력 벡터 뒤에 위치하여야 하며, Fig. 7의 왼쪽 과 같이 4절링크의 순간중심점의 x값(ICR_x)과 L2의 연 장선과 지면 반발력 벡터가 만나는 점의 x값(GRFV_x)의 차가 최소 일정값(x_th)이 되어야한다. 이를 수식으로 표 현하면 식 (2)와 같다.

Fig. 7

Cost Functions of Novel 4-bar Linkage Mechanism

$\[ \begin{array}{l}IC{R}_x=\frac{x_2\cdot \tan \gamma -x_1\cdot \tan \phi +\left(y_1-y_2\right)}{\tan \gamma -\tan \phi }\\ where,\phi ={\theta }_{12}-{\theta }_A,\\ \gamma ={\theta }_{23}-{\theta }_c-{\theta }_A\\ GRF{V}_x=\frac{y_1-x_1\cdot \tan \phi }{\frac{\left|V_y\right|}{\left|V_x\right|}-\tan \phi }\\ To\min imizeIC{R}_x-GRF{V}_x-x_{th}\end{array} \]$

(2)

여기서, x_th는 착용자들의 다양한 보행방법에 따른 지면 반발력 벡터의 변화로 인하여 순간중심점이 벡터 앞으 로 이동될 수 있으므로 이를 방지하기 위한 안전 최소치 를 부여한 값이며, P₁(x₁, y₁), P₂(x₂, y₂)는 링크의 회전 점 좌표 값, γ와 φ는 각 링크의 직선의 방정식을 구하기 위한 기울기 값이다. 식 (2)의 ICR_x식은 L₁과 L₂의 직선 의 방정식의 교점식을 나타낸것이며 GRFV_x식은 지면 반발력 벡터와 L₂의 직선의 방정식과의 교점을 나타낸 다. 마지막 식은 동적 안정성의 목적함수(F₁)로써 r_stability 의 양수 값중 가장 큰 값을 갖는 체중부하기와 중간입각 기 구간 안에서의 함수이며, 이때의 발목 각도(θ_A)와 지 면 반발력 벡터(V₁, V₂)의 좌표값은 r_stability값이 가장 큰 구간의 보행실험 데이터 값을 적용하였다.

2.3.2. 운동학적 유사성의 목적함수

유각기 구간에서는 Fig. 7의 오른쪽과 같이 4절 링크 중 L₂와 연결된 발목 관절의 궤적이 인체의 발목 궤적과 유사하여야 하며, 식 (3)과 같이 두 궤적 사이의 잔차 (residual)들의 평균인 평균 제곱근 편차(root mean square deviation, RMSD)의 최소값을 운동학적 유사성의 목적 함수(F₂)로 선정하였다.

$\[ To\min imize={\displaystyle \sum _{i=1}^{32}\sqrt{{\left(R{F}_{x_i}-K_{x_i}\right)}^2+{\left(R{F}_{y_i}-K_{y_i}\right)}^2}} \]$

(3)

여기서, 인체 발목관절의 궤적 데이터인 RF_x, RF_y의 샘 플링 개수는 32개이며 보행실험 데이터 값이다. 또한, 4절 링크와 연결된 로봇의 발목 관절 궤적 데이터인 K_x, K_y은 운동학적 모델링을 통하여 구하였다.

2.3.3. 최적화 결과

위의 설계변수와 목적함수에 대한 정식화는 식 (4)와 같다.

$\[ \begin{array}{l}\begin{array}{ll}Find\hfill & l_1,l_2,l_3,{\theta }_{12},{\theta }_{23},{\theta }_C\hfill \\ To\min imize\hfill & F_1+F_2\hfill \\ Subjectto\hfill & 65\le {\theta }_{12}\le 85,90\le {\theta }_{23}\le 120,\hfill \end{array}\\ 40\le l_1,l_2,l_3\le 55,10\le {\theta }_C\le 30,\\ 20\le l_2-l_1\cdot \cos {\theta }_{12}+l_3\cdot \cos {\theta }_{23},\\ 10\le l_1-l_3\end{array} \]$

(4)

각각의 설계 변수들의 구속 범위는 4절 링크와 내부 링크의 설계 공간을 감안하여 설정하였다.

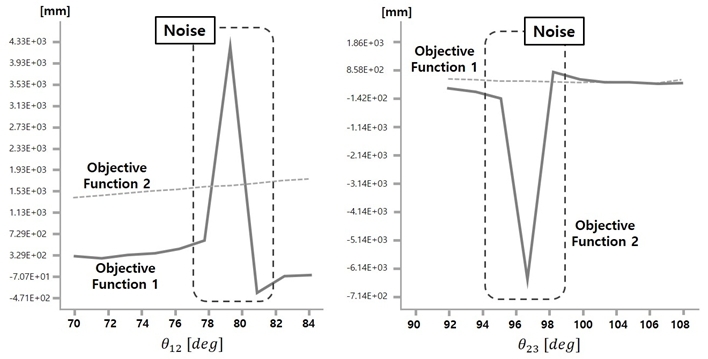
본 연구에서는 최적화를 위해 PIDO (process integration and design optimization) 툴인 PIAnO (process integration, automation and optimization) 툴을 이용하여 최적화를 진행하였다^[12]. 최적화 기법을 선정하기 위해 설계 변수 들의 입력 값에 따른 목적함수의 응답 경향성을 파악하 는 파라메트릭 스터디(parametric study)를 적용하여 목 적함수들의 수치적 노이즈 존재여부를 조사하였다. 그 결과 Fig. 8과 같이 설계 변수들 중 초기링크 각도인 θ₁₂, θ₂₃에 대한 목적 함수의 노이즈가 발생하였다. 이러 한 노이즈가 포함된 최적화 문제를 효과적으로 해결하 기 위해 점진적 이차반응 표면 방법(progress quadratic response surface method, PQRSM) 기법을 적용하였다^[13].

Fig. 8

Noise of the Design Variable for the Objective Functions

설계 변수들의 최적화 된 값들을 Table 1로 정리하였 다. Fig. 9의 왼쪽과 같이 최적화된 4절링크의 유각기 궤적은 인체의 발목 궤적과 유사하게 도출되었으며, 동 시에 Fig. 9의 오른쪽과 같이 입각기의 의 양수 값이 가 장 큰 구간에서 4절링크의 순간 중심점을 지면 반발력 벡터의 후면으로 이동하여 동적 안정성을 확보하였다.

Table 1

Result of Optimization Design

Fig. 9

Result of Optimization for Each Objective Functions

3. 실험 및 결과

최적화된 설계 값을 기준으로 상세 설계를 진행하였 으며 실 제작을 진행하였다. Fig. 10과 같이 입각기 구간 에서는 내부 링크에 의해 후방 링크가 캠 메커니즘의 형상에 따라 이동되어 4절링크의 순간 중심점을 후면으 로 이동시킨다. 또한, 유각기 구간에서는 후방 링크가 초기 위치로 이동되어 인체의 무릎 구조와 유사하게 굴 곡된다.

Fig. 10

Detail Design of Novel 4-bar Linkage Mechanism

실 제작한 무릎 메커니즘은 고 관절과 발목 관절이 근력 지원이 되는 외골격 로봇에 부착하였으며, 무릎 관 절과 발목 관절 사이에 길이 조절이 가능하도록 제작하 여 착용자 맞춤이 가능케 하였다. 실험을 위해 절삭작업 을 위한 툴을 Zero G 메커니즘과 함께 전면에 부착하였 다. 본 절에서는 개발된 4절 무릎메커니즘이 하중을 지 면에 전달하여 착용자의 근력을 지원하는지 확인하기 위해 Tekscan사의 발의 압력측정 센서인 F-Scan 장비를 사용하여 Fig. 10와 같이 착용자의 신발안에 센서를 부 착하였다. 이는, 본 연구의 메커니즘이 적용된 외골격 로봇을 착용함으로써 착용자가 하중을 받지 않고 근력 지원 여부를 확인하고자 하였다. 실험은 84 kg의 체중인 피험자가 총 2가지(기립, 보행)에 대하여 외골격 로봇과 10 kg의 작업툴 사용여부에 대한 4가지 상황을 실험하였다.

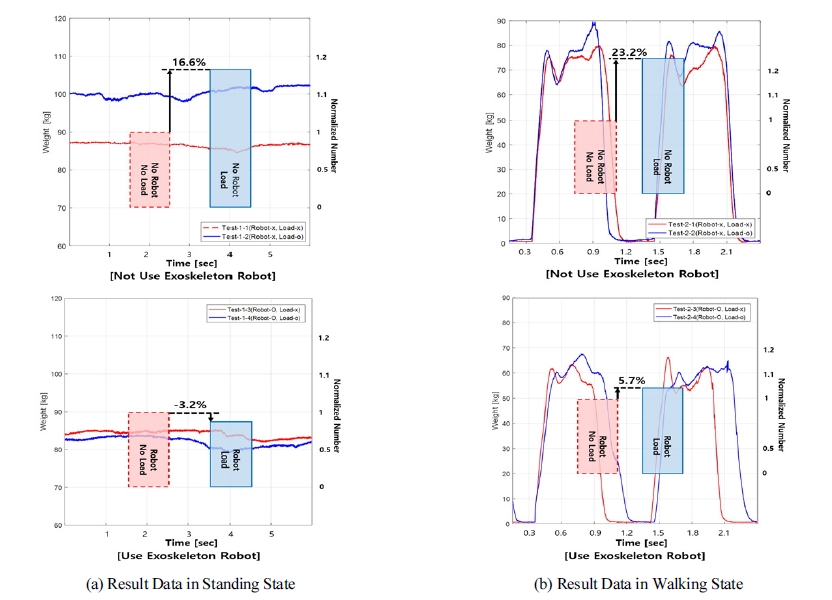
Fig. 11과 같이 4가지 상황에서 시간에 대한 기립자세 와 보행의 센서값 결과를 그래프화 하였다. 실선은 센서 값이고 막대 그래프는 센서 값을 정규화하였다. Fig. 11 의 (a)는 기립상태에서의 로봇 착용여부에 대한 근력지 원을 측정한 것이다. 미 착용시 외부하중에 대한 피험자 의 무게는 16.6% 증가하였으며 이는 하중이 피험자에게 가해짐으로써 센서 값이 증가하였다. 하지만 착용 후 외 부하중에 대한 피험자의 무게는 3.2% 감소하였으며 이 는 외부하중이 피험자에게 가하지 않고 로봇의 링크를 통하여 지면으로 전달되었다. Fig. 11의 (b)는 보행상태 에서의 로봇 착용여부에 대한 근력지원을 측정한 것이 다. 미 착용시 외부하중에 대한 피험자의 무게는 23.2% 증가하였지만, 착용 후 외부하중에 대한 피험자의 무게 는 5.7% 증가로 외부하중에 대한 피험자의 무게 증가는 발생하지 않았다.

Fig. 11

Result Data of Insole-type Sensor in Walking and Standing

4. 결 론

본 연구는 작업툴 작업을 위한 기립자세와 중량물 이 송에 대한 보행에서 근력을 지원하는 링크의 회전 중심 의 가변이 가능한 무릎 관절 메커니즘을 개발하였다. 본 메커니즘의 설계를 위해 PIAnO 툴을 이용하여 최적화 설계를 진행하였다. 도출된 설계 값은 유각기 구간내 착 용자의 무릎 관절 구조와 유사하게 움직여 이질감을 줄 였고 입각기 구간내에서는 동적 안정성을 확보하여 수 동적 지지력으로 착용자의 근력을 지원하였다. 본 메커 니즘의 근력 지원 검증을 위해 신발 안창형 센서를 부착 하여 기립과 보행에 대한 발바닥 힘을 측정하였다. 그 결과 본 연구의 메커니즘이 부착된 외골격 로봇을 착용 시 작업툴의 하중이 지면에 전달됨으로써 착용자의 근 력지원에 대한 검증이 이루어졌다.

Acknowledgments

This project was funded by National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No.NRF-2015R1A2A2A 01002887)

References

• Lee, H.-D, Han, C.-S, Technical Trend of the Lower Limb Exoskeleton System for the Performance Enhancement, Journal of Institute of Control, Robotics and Systems, (2014, March), 20(3), p364-371. [https://doi.org/10.5302/j.icros.2014.14.9023]
• Kim, W.-S, Lee, H.-D, Lim, D.-H, Han, J.-S, Han, C.-S, Mechanical Design of the Hanyang Exoskeleton Assistive Robot (HEXAR), (2014), International Conference on Control, Automation and Systems, Seoul, South Korea, p479-484. [https://doi.org/10.1109/iccas.2014.6988049]
• Van Dijk, W, Van Der Kooij, H, Hekman, Edsko, A Passive Exoskeleton with Artificial Tendons: Design and Experimental Evaluation, IEEE International Conference on Rehabilitation Robotics, July, 2011, Zurich, Switzerland.
• Valienete, Andrew, Design of a Quasi-Passive Parallel Leg Exoskeleton to Augment Load Carrying for Walking, Master's Thesis, (2005).
• Young, Aaron J, Ferris, Daniel P, State-of-the-art and Future Directions for Lower Limb Robotic Exoskeletons, IEEE Transactions on Neural Systems and Rehabilitation Engineering, (2016), 25(2), p171-182. [https://doi.org/10.1109/tnsre.2016.2521160]
• Crowell, Harrison P, Boynton, Angela C, Michael, Mungiole, Exoskeleton Power and Torque Requirements Based on Human Biomechanics, [Online]. Available: https://permanent.access.gpo.gov/gpo2634/ARLTR-2764.pdf, (2002), 11.
• Kirtley, C, Clinical gait analysis: theory and practice, Elsevier Health Sciences, (2006), p170-173.
• Stewart, RE, Staros, A, Selection and Application of Knee Mechanisms, Prosthetic and Sensory Aids Service, Medical Research in the Veterans' Administration, United States, (1972), p90-158.
• Munoz-Cesar, Juan Jose, Hernandes-Gomez, Luis Hector, Optimization of the Design of a Four Bar Mechanism for a Lower Limb Prosthesis Using the Taboo Search Algorithm, Advances in Bio-Mechanical Systems and Materials, (2013, August), 40, p107-125. [https://doi.org/10.1007/978-3-319-00479-2_9]
• Walker, P.S, Kurosawa, H, Rovick, J.S, Zimmerman, R.A, External Knee Joint Design Based on Normal Motion, Journal of Rehabilitation Research and Development, (1985), 22, p9-22. [https://doi.org/10.1682/jrrd.1985.01.0009]
• Radcliffe, C.W, Four-bar Linkage Prosthetic Knee Mechanisms: Kinematics, Alignment and Prescription Criteria, Prosthetics and Orthotics International, (1994), p159-173.
• Progress Integration, Automation and Optimization - PIAnO, User's Manual, FRAMAX Inc, (2009).
• Hong, K.-J, Kim, M.-S, Choi, D.-H, Efficient Approximation Method for Constructing Quadratic Response Surface Model, Journal of Mechanical Science and Technology, (2001, July), 15, p876-888. [https://doi.org/10.1007/bf03185266]