다차원 경로격자지도를 이용한 주차 경로계획 알고리즘

1. 서 론

최근 자동차의 자율주행 연구에는 이동로봇에서 사용 되는 기술이 활발하게 도입되고 있다^[1-2]. 그 중에서 자동 주차를 위한 경로계획 분야는 차량이 목표 위치에 주차 하기 위한 이동경로를 계획하는 분야로, 차량의 기구학 적인 특성을 고려하여 경로를 계획하는 것이 중요하다. 기존에 연구되었던 차량을 위한 경로계획법은 크게 샘 플링 기반의 경로계획법과 탐색 기반의 경로계획법으로 나뉜다.

대표적인 샘플링 기반의 경로계획법은 RRT (Rapidly exploring Random Trees) 기법^[3]으로 다양한 운동 모델 에 쉽게 적용이 가능하다는 장점이 있다. 그러나 샘플링 기반의 경로계획법의 특성상 생성된 경로와 수행시간을 예측하기 어렵고, 실제로 생성된 경로가 최단거리인지 알 수 없다는 단점이 있다.

대표적인 탐색 기반의 경로계획법에는 Hybrid A* 알 고리즘^[4]이 있다. Hybrid A* 알고리즘은 A* 알고리즘^[5] 을 기반으로 하는 탐색 알고리즘으로, 최소 비용을 가지 는 경로를 탐색하는 기법이다. Hybrid A* 알고리즘은 기존의 A* 알고리즘과 다르게 차량의 이동 제약을 고려 하고, 휴리스틱 비용을 사용하여 계산속도가 빠르며, 다 양한 환경에서 활용이 가능하다는 장점이 있다. 그러나, 주차환경이 넓어짐에 따라 필요한 메모리와 연산량이 크게 증가하는 단점이 있다.

본 논문에서는 연산량이 적으면서 다양한 주차 방식 에 맞는 최적의 경로를 생성하는 방법을 제안하다. 제안 한 방법은 차량의 기구학적인 요소를 고려한 경로격자 를 이용하여 환경을 구성하고, A* 알고리즘을 사용하여 최소 비용을 가지는 경로를 탐색하는 방법이다. 제안한 경로계획법은 Hybrid A* 알고리즘과 달리 경로격자라 는 새로운 개념을 도입하여 노드 위치에 대한 계산 과정 을 단순화하여 연산량을 감소시켰으며, 차량의 기구학 적인 특성을 고려하여 실제 차량이 추종할 수 있는 경로 계획이 가능하다. 또한, 경로격자를 이용하여 작성한 다 층 구조의 다차원의 경로 격자지도는 다양한 환경에서 도 경로계획이 가능하게 하였다.

본 논문은 다음과 같이 구성된다. 2장에서는 차량의 기구학적 특성을 이용하여 생성한 경로격자에 대해 설 명을 하고, 3장에서는 다차원 경로 격자지도를 작성하는 방법에 대해 설명을 한다. 그리고 4장에서는 경로격자 기반의 경로계획법에 대해 설명한다. 5장에서는 경로 보 간법에 대해 설명을 하고, 6장과 7장에서 실험 결과 및 결론을 도출한다.

2. 차량의 기구학적 특성을 이용한 경로격자

차량에 적합한 경로계획법은 차량의 non-holonomic 구속조건에 의한 이동 제약을 고려해야 한다. 따라서 본 연구에서는 차량의 기구학적 특성을 고려하여 차량의 경로격자를 생성하고, 이를 경로계획법에 활용한다.

2.1. 차량의 기구학적 특성

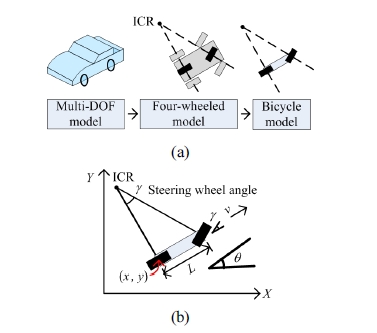
자동주차 과정에서 차량은 저속으로 이동하므로 복잡 한 다자유도 차량 모델이 아닌 Fig. 1(a)과 같은 3자유도 의 bicycle 모델로 모델링이 가능하다^[6]. 3자유도 차량 모델은 차량의 좌우 조향 바퀴의 각도를 평균하여 구성 한 이륜 자동차 형태이며, 3자유도 차량 모델의 운동방 정식^[7]은 다음과 같다.

Fig. 1

Motion model: (a) simplified model, (b) bicycle model

$\[ \begin{array}{l}\dot{x}=v\text{\hspace{0.17em}cos\hspace{0.17em}}\theta \\ \dot{y}=v\text{\hspace{0.17em}sin\hspace{0.17em}}\theta \\ \dot{\theta }=\frac{v}{L}\text{tan\hspace{0.17em}}\gamma \end{array} \]$

(1)

여기서 x, y는 Fig. 1(b)와 같이 차량의 뒷바퀴 축의 중심 위치이고, θ는 차체의 각도이다. 또한 v는 차량의 속도 를, L은 앞바퀴과 뒷바퀴 사이 거리를, γ는 조향 바퀴의 각도를 나타낸다. 이 때, 차량의 바퀴는 횡방향 슬립이 없다고 가정한다. 이렇게 정의된 식 (1)을 사용하면, 차 량의 non-holonomic 구속조건을 고려한 이동경로를 계 산할 수 있다.

2.2. 경로격자 생성

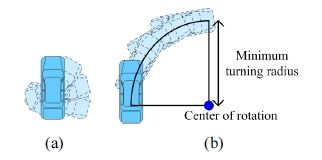
차량을 위한 경로계획법은 차량이 Fig. 2와 같이 회전 할 때, 발생하는 회전 한계를 고려해야 한다. 차량은 구 조적 특성으로 인해 Fig. 2(a)와 같이 제자리 회전이 불가 능하며, 조향 바퀴의 각도, 차체의 길이 등에 의해 Fig. 2(b)와 같이 회전할 수 있는 최소반경이 정해진다.

Fig. 2

Rotational motion of vehicle

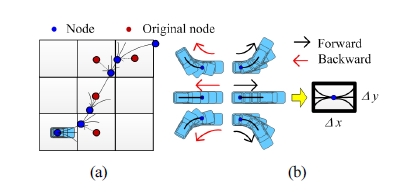
일반적으로 차량의 경로계획법은 차량의 연속적인 상 태를 고려하여 작성하는 것이 필요하므로, 기존에 연구 되었던 Hybrid A*에서는 Fig. 3(a)와 같이 정해진 노드 를 차량의 이동경로에 맞게 변경해주는 작업이 필요하 다. 하지만 이러한 과정은 많은 연산량을 필요로 하기 때문에 실제 차량에 적용하기에는 적합하지 않다. 본 논 문에서는 위와 같은 연산을 줄이고, 차량의 주행 안정성 과 기구학적인 특징을 고려한 경로를 생성하기 위해서 Fig. 3(b)와 같이 차량의 이동 경로를 나타내는 영역을 정의하여, 이를 ‘경로격자’라고 명명하였다.

Fig. 3

Comparison between nodes of (a) Hybrid A* and (b) path grid

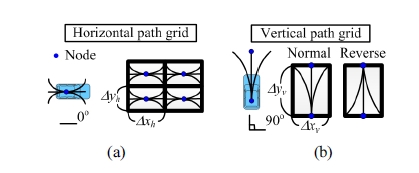
본 논문에서 제안하는 경로격자는 수평 경로격자와 수직경로격자로 구성되어 있다. 수평 경로격자는 Fig. 4(a) 와 같이 격자의 중심에 노드를 가지고 있으며, 차체의 각도가 0° 또는 180°일 때, 차량이 이동 가능한 6방향의 경로가 포함되어 있다. 반면에, 수직 경로격자는 Fig. 4(b) 와 같이 격자 양 단에 노드들을 가지고 있으며, 차체의 각도가 90° 또는 270° 일 때, 차량이 이동 가능한 3방향 의 경로가 포함되어 있다. Fig. 4(b)와 같이 수직 경로격 자는 정방향과 역방향의 두 가지 상태가 존재한다. 경로 격자는 최소 회전반경을 고려한 차량이 현 위치에서 이 동할 수 있는 최대 영역을 나타낸다.

Fig. 4

Path grid: (a) Horizontal grid, (b) Vertical grid

수평 경로격자의 크기는 식 (1)의 차량 운동방정식을 이용하여 다음과 같이 계산된다.M2

$\[ \begin{array}{l}\Delta x_h=\frac{L}{\text{tan\hspace{0.17em}}{\gamma }_{\max }}\text{sin\hspace{0.17em}}\Delta \theta \times 2\\ \Delta y_h=\frac{L}{\text{tan\hspace{0.17em}}{\gamma }_{\max }}\left(1-\text{cos\hspace{0.17em}}\Delta \theta \right)\times 2\end{array} \]$

(2)

여기서 Δx_h와 Δy_h는 수평 경로격자의 가로 및 세로 길 이를 각각 나타낸다. 격자의 크기는 차량의 속도가 일정 하고, 차량의 각도 변화량이 0이 아니라는 가정 하에 계 산된다. 양 옆으로 이동하는 경로는 차량의 조향 바퀴를 최대한 돌린 채로 이동을 하였을 때, 차량의 경로를 나타 낸다.

수직 경로격자의 크기는 다차원 경로격자지도를 작성 할 때, 수직격자와 수평격자의 배열을 맞추기 위해 다음 과 같은 관계로 정의한다.M3

$\[ \begin{array}{l}\Delta x_v=\Delta x_h\\ \Delta \text{}{y}_v=k_v\Delta y_h\end{array} \]$

(3)

여기서 Δx_v와 Δy_v는 수직경로격자의 가로 및 세로 길이 를 각각 나타낸다. 또한, 비례상수 k_v는 수평격자의 노드 에서 수직격자의 노드까지 차량이 이동했을 때, 수직격 자의 노드 위치에서 차량의 각도가 90° 또는 270°가 되 도록 수평격자와의 비율을 맞춰주는 비례상수이다.

3. 차량의 경로계획을 위한 다차원 경로격자지도

본 연구에서는 격자지도와 경로격자를 이용하여 다차 원 경로격자지도를 작성하는 방법을 제안한다. 이 기법 은 다양한 주차환경에서 최적의 경로를 생성하기 위해 서 경로격자를 사용하였고, 단일 층의 경로격자지도로 는 계산하기 어려운 경로를 다층으로 확장하여, 최적의 경로를 좀더 쉽고 간단하게 계산하도록 하여 연산량을 감소시켰다.

3.1. 격자지도

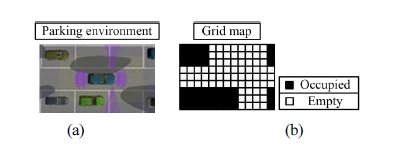
격자지도는 환경을 일정한 크기의 격자로 나누고, 흰 색은 비점유영역, 검은색은 점유영역을 나타낸다^[8]. 예 를 들어, Fig. 5(a)와 같은 환경이 주어지면 작성된 격자 지도는 Fig. 5(b)와 같이 작성된다.

Fig. 5

Example of grid map: (a) Environment, (b) grid map

3.2. 다차원 경로격자지도

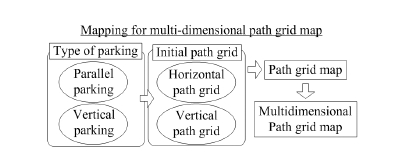
다차원 경로격자지도는 경로격자를 다층 구조로 작성 한 지도로, 각 층에는 수평경로 격자지도와 각기 다른 수직경로 격자지도로 구성되어 있다. 다차원 경로격자 지도는 Fig. 6과 같은 순서로 작성된다. 우선, 주차방법 에 따라 적절한 초기 경로격자를 선택하고, 초기 경로격 자를 기준으로 경로격자지도를 작성한다. 마지막으로 작성한 경로격자지도는 확장을 통해 다차원 경로격자지 도로 작성된다.

Fig. 6

Process of mapping for multidimensional path grid map

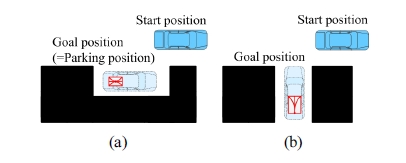
초기 경로격자는 Fig. 7과 같이 경로격자의 노드 방향 과 주차 방향이 일치하도록 경로격자를 선택한다. 한 예 로 Fig. 7(a)와 같이 평행주차는 수평격자를, Fig. 7(b)와 같이 수직주차는 수직격자를 초기 경로격자로 사용한다.

Fig. 7

Initial setting for parking: (a) parallel parking, (b) vertical parking

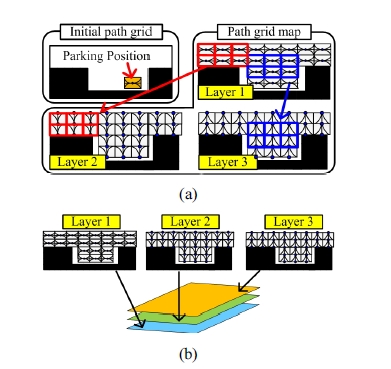
정해진 초기 경로격자를 기준으로 경로격자지도와 다 차원 경로격자지도를 작성한다. 예를 들어, 수직경로격 자의 비례상수 k_v가 1일 때, 평행주차를 위한 다차원 경 로격자지도는 Fig. 8과 같이 작성된다. 경로격자지도는 Fig. 8(a)와 같이 주차지점을 기준으로 1층 경로격자지도 를 생성한다. 이때, 경로격자지도는 차량의 충돌 안전성 을 위해 경로격자 내에 장애물(점유격자)이 존재하지 않 는 경로격자들로만 구성된다. 2층 경로격자지도는 작성 된 1층 지도의 붉은색 표시와 같이 수평격자 간격에 맞 도록 수직격자를 배치하여 작성한다. Fig. 8(a)의 3층 경 로격자지도도 2층 지도와 마찬가지로 Fig. 8(a)에서 파란 색 표시와 같이 수직격자를 배치하여 작성한다. 작성된 각기 다른 경로격자지도는 Fig. 8(b)와 같이 합하여 다차 원 경로격자지도를 구성한다. 이와 같이 구성된 다차원 경로격자지도를 경로계획에 사용할 경우, 단일 경로격 자지도만을 사용하는 것보다 차량의 다양한 움직임을 표현할 수 있다.

Fig. 8

Mapping for multidimensional path grid map

4. 경로격자를 이용한 경로계획법

제안한 다차원 경로격자지도를 이용한 경로계획법은 A* 기반의 알고리즘을 기반으로 노드를 확장하고, 주행 비용을 계산하여 사용한다.

4.1. 노드 확장

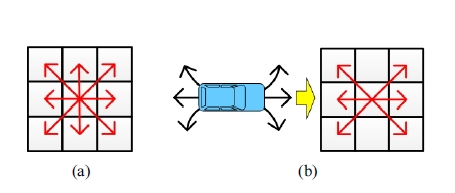
A* 알고리즘은 각 노드의 주행비용을 계산하여 최소의 비용을 가지는 노드를 선택하고, 그 노드를 기준으로 확장 하는 과정을 반복한다. 이 과정에서 기존의 A* 알고리즘의 경우에는 Fig. 9(a)와 같이 한 노드를 중심으로 8방향으로 확장하였다. 그러나 본 연구에서는 차량의 non-holonomic 특성을 고려하여 Fig. 9(b)와 같이 6방향으로만 노드를 확 장하여 사용한다.

Fig. 9

Direction of expansion node: (a) A*, (b) path grid

4.2. 주행비용

제안한 방법은 A* 알고리즘의 주행비용에 차량 모델 에 대한 비용을 추가하여 경로계획을 수행하였다. 주행 비용은 인접비용, 휴리스틱 비용(heuristic cost), 후진비 용(backward cost), 그리고 전환비용(switching cost)으로 구성되어 있다. 인접비용(adjacency cost)은 출발위치에 서 각 격자에 도달하는 비용이고, 휴리스틱 비용은 각 격자에서 목표점까지의 직선거리에 해당하는 비용을 나 타낸다.

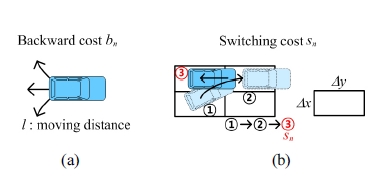
후진비용과 전환비용은 모두 차량의 진행 방향에 관 련된 비용으로, 후진비용은 Fig. 10(a)와 같이 차량이 전 진이동이 아닌 후진이동을 할 때, 이동한 거리에 비례하 는 비용 b_n을 부과한다.M4

Fig. 10

(a) Backward cost and (b) switching cost

$\[ b_n=\{\begin{array}{ll}{k}_b\times l,\hfill & \text{backward}\hfill \\ 0,\hfill & \text{forward}\hfill \end{array} \]$

(4)

여기서 l은 전 노드에서 n번째 노드로 이동하는 데 걸리 는 거리를, k_b는 이동거리와 후진비용 간의 비례상수를 나타낸다. 본 연구에서는 비례상수를 1로 설정하였다. 후진비용은 차량이 후진이동보다는 전진이동을 하도록 유도하는 역할을 한다.

전환비용은 차량이 Fig. 10(b)의 ③번과 같이 진행 방 향이 바뀔 때, 부여되는 비용으로, 방향 전환이 많을수 록, 사용하는 경로격자의 크기가 클수록 더 높은 비용 sn이 부여된다.M5

$\[ s_n=\{\begin{array}{l}N\times k_s\times \sqrt{\Delta x^2+\Delta y^2},\text{\hspace{1em}when\hspace{0.17em}switching}\\ \text{0,\hspace{1em}otherwise}\end{array} \]$

(5)

여기서 Δx와 Δy는 경로격자의 크기를, N은 방향전환 횟수를, k_s는 격자 크기와 전환비용 간의 비례상수를 나 타낸다. 전환비용은 차량이 방향전환을 최소로 하면서 이동하도록 유도하는 역할을 한다. 또, 전환비용의 비례 상수는 차량이 다시 제자리에 돌아오기 위한 최소 거리 비용보다 커야 하므로 본 연구에서는 2로 설정하였다.

앞서 언급한 인접비용과 휴리스틱 비용, 후진비용과 전환비용을 더하여 다음과 같이 주행비용을 계산할 수 있다.M6

$\[ f_n=g_n+h_n+b_n+s_n \]$

(6)

여기서 f_n은 n번째 노드의 주행비용을, g_n은 n번째 노드 의 인접비용을, h_n은 n번째 노드의 차량 모델을 위한 휴 리스틱 비용을 나타낸다.

4.3. 경로격자를 이용한 경로계획

경로계획은 노드 확장과 주행비용 계산을 반복하면서 수행된다. 자동주차를 위한 경로계획은 도착지점에서 차량의 위치와 각도가 중요하므로 도착지점에서부터 노 드 확장을 수행한다. 이와 같은 과정을 확장된 노드가 시작 위치에 도달할 때까지 반복하여 수행한다.

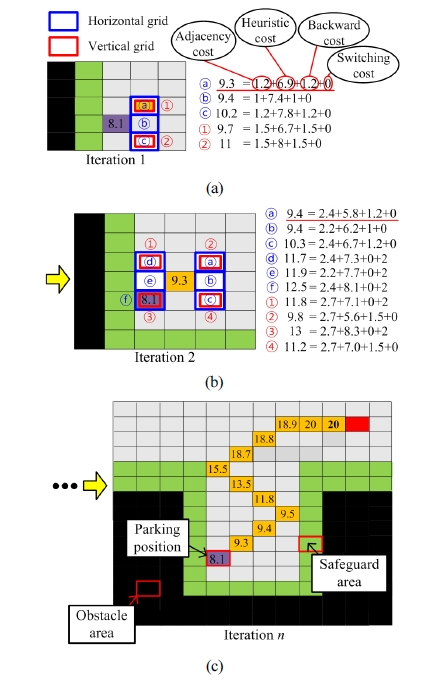
실제 주행비용은 Fig. 11과 같이 계산된다. Fig. 11에 서 검은색 경로격자는 실제 장애물을 나타내고, 녹색 경 로격자는 충돌 위험이 높은 영역을 나타낸다. 장애물과 충돌위험이 높은 녹색 격자는 이 격자 위로 경로가 생성 되지 않도록 하여 장애물과의 충돌을 방지하는 역할을 한다. 예를 들어, Fig. 11(a)와 같이 도착 위치인 보라색 격자에서 노드 확장을 하면 녹색 격자를 포함하지 않는 5개의 격자(ⓐ, ⓑ, ⓒ, ①, ②)로 확장된다. 확장된 격자 들의 주행비용은 Fig. 11(a)와 같이 계산되고, 그 중 주행 비용이 최소인 파란색 ⓐ격자가 주행비용이 최소인 격 자로 선택된다. 이때, ⓐ, ⓑ, ⓒ, …와 같은 격자들은 수평격자를, ①, ②, ③, …와 같은 격자들은 수직격자를 나타낸다. 이전 과정에서 선택된 ⓐ격자를 중심으로 다 시 노드 확장을 하여 주행비용을 계산하면 Fig. 11(b)와 같이 ⓐ격자가 선택된다. 이와 같은 과정들을 반복하면 Fig. 11(c)와 같은 결과를 얻을 수 있다.

Fig. 11

Process of calculating grid cost for parallel parking

마찬가지로 수직주차의 경우에는 앞서 언급했듯이 출 발지점에는 수평격자를 두고, 도착지점에 수직격자를 두어 경로 계획을 수행한다.

5. 경로격자를 이용한 경로 보간법

경로격자를 이용하여 생성된 경로는 차량의 최대 조 향각을 기반으로 계산되어 실제 차량이 추종하기에 다 소 비효율적이다. 또한, 본 논문에서 제안한 경로격자는 정확한 출발위치를 반영하지 못하므로 경로 보간을 통 하여 경로를 보정하는 작업이 필요하다. 경로 보간법은 출발점에 인접한 격자의 종류와 출발점의 상대적인 위 치에 따라 경로 보간법이 나뉜다.

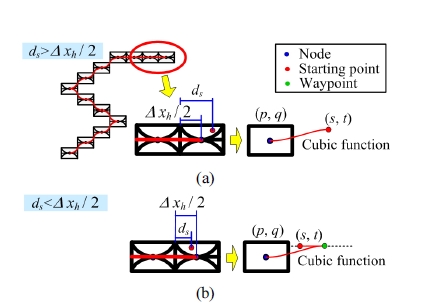
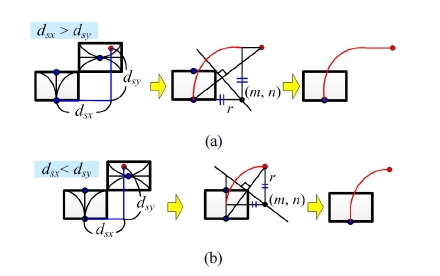
Fig. 12(a)와 같이 인접한 격자가 수평격자이면서, 경 로격자의 경계에서 출발지점까지 거리 d_s가 수평경로격 자 가로 길이의 절반인 Δx_h / 2 보다 클 경우에는 인접한 격자의 노드와 실제 출발점을 지나는 3차 곡선을 계산하 여 경로를 생성한다. 제안한 수평격자의 특성으로 인하 여 출발점과 수평격자의 노드에서 차량의 각도는 0°이 다. 따라서 이 두 점을 지나는 3차 곡선은 두 점의 위치와 기울기 조건을 통해 다음과 같이 구할 수 있다.

Fig. 12

Methods of path smoothing: Horizontal path grid

여기서 식 (7)은 새로 생성된 경로를 나타내고, 식 (8)의 조건을 만족한다. Fig. 12(b)와 같이 인접한 격자가 수평 격자이면서, 길이 d_s가 길이 Δx_h /2보다 짧을 경우에는 실제 차량의 최소 회전반경보다 짧은 회전반경이 필요 하게 된다. 따라서 출발점과 같은 높이의 직선에 도달하 는 경유점을 선정하여 그 점까지 3차 곡선을 생성하고, 출발점과 경유점을 이어서 경로 보간을 수행한다.

출발점과 수직격자가 서로 인접하였을 때는 Fig. 13과 같이 수직격자의 노드에서 차량의 각도가 90°이므로 이 두 점을 지나는 원주와 직선 식을 이용하여 경로를 보간 한다.M9M10

Fig. 13

Methods of path smoothing: Vertical path grid

여기서 d_sx와 d_sy는 출발점과 격자노드 사이 거리의 가로 및 세로 길이를 각각 나타낸다. 또, (m, n)은 출발점과 수직격자의 노드를 잇는 선분과 수직한 직선 위의 한 점을 나타낸다. 또, r은 (m, n)을 중심으로 하는 원형 경 로의 반지름을 나타낸다. d_sx와 d_sy의 크기에 따라 Fig. 13(a), (b)와 같이 경로 보간법이 나뉜다. 각각 생성한 원형 경로와 d_sx와 d_sy의 길이 차를 이용하여 경로 보간을 수행한다.

6. 실험 및 결과

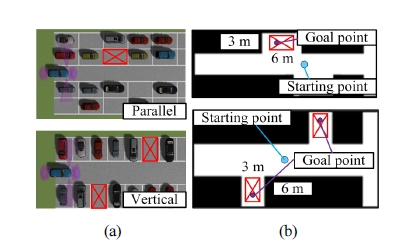
본 논문에서는 경로격자를 이용하여 자동주차를 위한 경로계획법의 성능을 시뮬레이션을 통해 검증하였다. 시뮬레이션은 차량용 시뮬레이션 프로그램인 Prescan을 사용하여 수행하였으며, 시뮬레이션 환경은 주차장법 시행규칙에 의거하여 일반형 평행 주차 넓이인 너비 2 m 이상, 길이 6 m 이상보다 약간 큰 3 m × 6 m 크기의 주차공간을 Fig. 14(a)와 같이 실제 주차환경과 비슷한 2가지 환경으로 구성하였다. 구성한 시뮬레이션 환경은 모두 격자지도로 나타내면 Fig. 14(b)와 같다.

Fig. 14

Experiment Environment: (a) simulation environment and (b) grid map

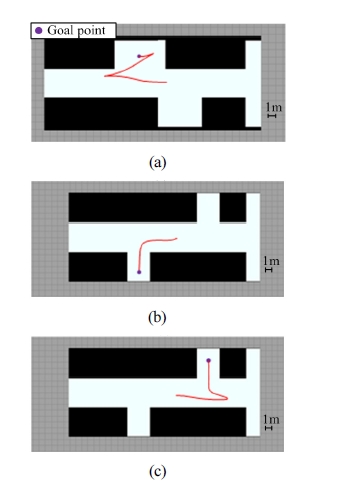
실험은 전폭 1.6 m, 전장 3.6 m, 축거 2.52 m인 실제 차량과 동일한 시뮬레이션 차량을 가지고 수행하였다. 주어진 시뮬레이션 환경에서 경로계획을 수행하면 Fig. 15와 같이 주차경로를 얻을 수 있다. Fig. 15는 각각의 출발점에서 도착점까지 생성된 경로를 나타낸 그림으로, 각각 Fig. 15(a)는 평행주차를, Fig. 15(b), (c)는 수직주차 를 위한 경로계획 결과이다. 이를 통해 본 연구에서 제안 한 경로격자를 이용한 경로계획법이 다양한 주차 방식 에 적용 가능하다는 것을 확인할 수 있다.

Fig. 15

Result of path planning for parking

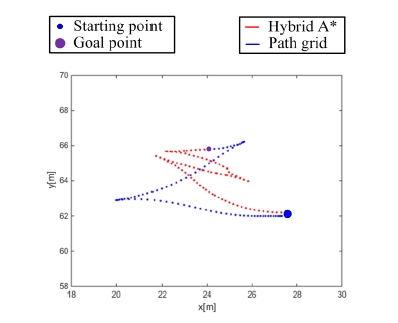
Fig. 16은 Fig. 15(a)와 같은 환경에서 제안한 방법과 Hybrid A* 알고리즘^[4]을 비교하여 나타낸 것이다. Fig. 16 에서 파란색 점과 보라색 점은 각각 출발점과 도착점을 나타내고, 붉은색 선은 Hybrid A*를 통해 생성된 경로를 나타내며, 파란색 선은 경로격자를 이용하여 생성된 경 로를 나타낸다. Table 1은 Fig. 15(a)에서 생성된 경로의 총 거리, 경로 생성시 Open-list에 포함된 노드의 수, 그 리고 경로 생성시간을 나타낸 것이다. 각각의 경로길이 는 Hybrid A*는 17.03 m, 경로격자는 15.94 m이었다. 경로격자를 이용한 경로계획법은 경로격자의 특성상 세 밀한 경로계획이 어려우므로 우회경로를 통해 주차 경 로를 생성하는 특성이 있다. 따라서 그래프에서 경로가 차지하는 영역을 보면 알 수 있듯이, 제안한 경로계획법 은 주차공간이 Hybrid A*에 비해 비교적 많이 필요하다 는 것을 알 수 있다. 그래프에서 보듯이 경로의 총 거리 와 방향전환 횟수는 경로격자를 이용한 경로계획법이 Hybrid A* 기법보다 적은 수치를 나타냈다. 이를 통해 주차에 소요되는 시간을 줄일 수 있어 효율적인 주차가 가능하다. 경로 생성 시 Open-list에 포함된 노드의 수는 경로격자가 다차원 지도를 사용하므로 약간 더 높게 나 오는 것을 알 수 있었다. 경로 생성시간은 다양한 환경에 서 출발점과 도착점 사이의 거리가 10 m 이내인 조건에 서 경로계획을 30회 반복하여 걸린 시간을 평균한 것으 로, 경로격자를 이용한 경로 생성시간이 Hybrid A*에 비해 짧은 것을 확인할 수 있다.

Fig. 16

Comparison of path planning based on (a) Hybrid A* & (b) proposed method

Table 1

Results of path planning

7. 결 론

본 논문에서는 경로격자를 이용한 자동주차 경로계획 법을 제안하였다. 제안된 경로 계획법의 성능은 시뮬레 이션을 통하여 입증하였으며, 다음과 같은 결론을 도출 하였다.

• (1)  제안한 방법은 평행주차와 수직주차(전면주차, 후면 주차) 모두 가능한 범용성이 우수한 경로 계획법이다.
• (2)  연속적인 차량의 위치정보에 경로격자를 이용하여 연산량과 수행시간을 줄임으로써 빠른 경로계획이 가능하다.

본 연구에서는 다양한 주차 방식에 대해 적용할 수 있 는 연산량이 적고, 수행시간이 빠른 경로계획법에 대해 연구하였다. 그러나 사용하는 알고리즘은 연산량을 줄 이기 위해 생성하는 경로를 단순화하여 사용하였다. 그 에 따라 생성된 경로가 다소 넓은 주차 공간을 필요로 하는 문제가 발생하였다. 따라서 추후 연구에서는 좀 더 좁은 주차 공간에서도 경로계획이 가능한 경로계획법에 대한 연구를 진행할 예정이다.

References

• Cho, Y, Roh, H.C, Chung, M.J, Accurate Parked Vehicle Detection using GMM-based 3D Vehicle Model in Complex Urban Environments, Journal of Korea Robotics Society, (2015), 10(1), p42-51. [https://doi.org/10.7746/jkros.2015.10.1.033]
• Park, S.-Y, Kim, S.-J, Lane-Level Positioning based on 3D Tracking Path of Traffic Signs, Journal of Korea Robotics Society, (2016), 11(3), p172-182. [https://doi.org/10.7746/jkros.2016.11.3.172]
• Pepy, R, Lambert, A, Mounier, H, Path planning using a dynamic vehicle model, Proc. 2nd ICTTA, (2006), p781-786.
• Dolgov, D, Thrun, S, Montemerlo, M, Diebel, J, Path Planning for Autonomous Vehicles in Unknown Semi-structured Environments, The International Journal of Robotics Research, (2010, April), 29(5), p485-501. [https://doi.org/10.1177/0278364909359210]
• Hart, P, Nilsson, N.J, Raphael, B, A Formal Basis for the Heuristic Determination of Minimum Cost Paths, IEEE Trans. Syst. Sci. Cybern, (1968, July ), 4(2), p100-107. [https://doi.org/10.1109/tssc.1968.300136]
• Jazar, R.N, Vehicle Dynamics: Theory and Application, (2009), New York, Springer. [https://doi.org/10.1007/978-0-387-74244-1]
• Corke, P.I, Robotics, Vision & Control: Fundamental Algorithms in MATLAB, (2011), Berlin, Springer.
• Thrun, S, Burgard, W, Fox, D, Probabilistic Robotics, (2005), Cambridge, The MIT Press.