두 개의 하이드로폰을 이용한 수중 음원 방향각 기반의 2차원 위치 인식 기법
© Korea Robotics Society. All rights reserved.
Abstract
Localization of underwater vehicle is essential to use underwater robotic systems for various applications effectively. For this purpose, this paper presents a method of two-dimensional SLAM for underwater vehicles equipped with two hydrophones. The proposed method uses directional angles for underwater acoustic sources. A target signal transmitted from acoustic source is extracted using band-pass filters. Then, directional angles are estimated based on Bayesian process with generalized cross-correlation. The acquired angles are used as measurements for EKF-SLAM to estimate both vehicle location and locations of acoustic sources. Through these processes, the proposed method provides reliable estimation for two dimensional locations of underwater vehicles. Experimental results demonstrate the performance of the proposed method in a real sea environment.
Keywords:
Underwater vehicle, SLAM, Localization, Acoustic source, Acoustic pinger1. 서 론
최근 해양 환경에 대한 관심이 증대됨에 따라 수중 로봇에 대한 활용 또한 증가되고 있다. 이러한 로봇 시스 템의 활용은 광물자원 채취, 심해저탐사, 해양구조물 검 사, 수중 건설 작업 등 다양한 분야로 확대되고 있으며, 이에 따라 로봇 시스템의 운영에 필요한 연구개발 역시 활발히 진행되고 있다. 로봇 시스템의 효과적인 활용을 위해서는 위치 인식 알고리즘의 개발이 필수적이다. 그 러나 해양 환경, 특히 수중 환경은 센서의 활용이 제한적 임으로 인해 안정적인 위치 인식 시스템의 구현이 쉽지 않다[1].
수중 환경에서는 전자기신호의 높은 감쇄율로 인해, GPS, 레이저 센서 등 지상 로봇에서 유용하게 사용되는 센서의 활용이 쉽지 않다. 뿐만 아니라, 탁도 등의 영향 으로 카메라 기반의 위치 인식 또한 매우 제한적으로 사용된다[2]. 이를 대신하여, 소나 영상이 사용되기도 하 지만 지상에서의 영상정보와 달리 해상도 및 포함된 정 보의 양이 부족하여 안정적인 정보를 제공하기에 쉽지 않다[3].
이로 인해 수중 환경에서는 음향 신호 기반의 센서 활용이 매우 중요하다[4,5]. 수중에서 음향신호는 빠른 전 달 속도와 함께 낮은 신호 감쇄율로 인해, 다양한 위치 인식 시스템에 적용되어 사용되어 왔다. 하지만, 전통적 으로 많이 사용되어 오는 장기선(Long Baseline, LBL) 등 의 시스템의 활용을 위해서는 작업 반경 내에서의 설치, 정확한 위치 획득, 오차 보정 등의 번거로운 작업이 동반되 어야 하며, 이러한 과정에서의 오차는 위치 인식 결과에 직접적으로 영향을 미치게 된다[6,7].
음향 신호의 활용은 베이스라인(baseline) 기반의 시스 템 외에도, 다양한 방법으로 수중 로봇의 항법 알고리즘 에 적용되기도 하였다[8]. LBL 시스템의 트랜스폰더의 기능을 이용하여 양방향 거리 정보를 이용한 위치 인식 시스템이 개발되어왔다[9]. 뿐만 아니라, 수중 음향 통신 에서 사용되는 모뎀의 기능을 통해 동기화된 정보로부 터 단방향 거리 정보를 획득하여 이를 위치 인식에 사용 되기도 하였다[10].
위에서 보인 예들과 같이, 수중 환경에서의 음향 신호의 활용은 필수적이다. 본 논문에서는 이러한 수중 음향 신호 기반의 위치 인식 기법을 제안한다. 제안된 방법은 비동기 화된 인공 수중 음원(pinger)을 이용하여 수행된다. 또한, 음원으로부터 발신된 음향 신호를 취득하기 위해 두 개 의 하이드로폰이 장착된 로봇 시스템을 이용한다.
제안된 방법은 비동기화된 수중 음원을 이용함에 따 라 비행시간법(Time of flight, TOF) 기반의 거리 정보의 활용이 불가능하다. 이렇게 TOF 기반의 거리 정보를 이 용할 수 없는 경우에는, 서로 다른 하이드로폰 간의 도달 시간지연을 이용한 방향각 정보의 활용이 가능하다. 앞 에서 언급한 바와 같이, 본 논문에서는 두 개의 하이드로 폰이 장착된 로봇 시스템을 대상으로 하였다. 따라서, 두 하이드로폰에서 수신된 음향 신호로부터 도달시간지 연을 획득하여 이로부터 수중 음원의 방향각 정보를 획 득하고, 이 방향각 정보를 활용한 위치 인식 기법을 제안 한다.
제안된 방법은 세 단계로 구성된다. 먼저, 하이드로폰 을 통해 취득된 수중 음향 신호로부터 방향각 추정의 대상이 되는 수중 음원에서 발신된 신호를 추출한다. 이 과정을 위해서는 대역통과필터와 함께 수신 신호의 신 호 세기 정보를 이용한다. 다음으로, 추출된 음향 신호로 부터 수중 음원의 방향각 추정을 위해 일반화된 상호상 관분석 정보와 함께 베이지안 프로세스를 통해 안정적 인 도달시간지연 정보를 획득한다. 해당 과정은 저자의 기존 연구를 활용하였다[11]. 이렇게 얻어진 도달시간지 연 정보는 수중 음속과 하이드로폰 간의 거리로부터 방 향각 정보 측정에 활용된다. 마지막으로, EKF (Extended Kalman Filter) 기반의 동시 자기 위치 인식 및 지도 작성 (SLAM) 알고리즘을 활용하여, 수중 음원의 위치와 함께 로봇의 2차원 위치를 추정한다. EKF기반의 SLAM을 위 해, 예측(prediction) 과정은 관성 센서 정보로부터 수행 되며, 보정(correction) 과정을 위해 수중 음원의 방향각 정보가 활용된다.
위의 과정을 통해 수행되는 제안된 방법은 수중 로봇 의 안정적인 위치 인식에 사용될 수 있으며, 다음과 같은 장점이 있다. 먼저, 관성 센서 정보와 수중 음원의 방향 각 정보를 융합한 기법을 통해 수중 로봇 자율 항법을 위한 안정적인 구조를 제공한다. 관성 센서 정보는 기본 적인 수중 로봇의 위치 추정을 제공하며, 외부 랜드마크 정보가 제공되지 않는 상황에서도 위치 추정을 제공한 다. 또한 수중 음원의 정보는 외부 랜드마크 정보로써 위치 추정의 오차가 누적되지 않고 한정될 수 있도록 한다. 다음으로, 수중 음향 장비를 정해진 위치에 놓아야 하는 베이스라인 기반 시스템과 달리, 임의의 위치에 설 치하고 이에 대한 위치 정보를 미리 획득할 필요가 없다. EKF 기반의 SLAM 알고리즘을 통해 수중 로봇의 위치 와 음원의 위치를 동시에 추정하기 때문이다. 마지막으 로, 위치 추정에서 측정값으로 사용된 베이지안 확률 기 반의 방향각 추정은 수중 음원의 방향각 정보를 안정적 으로 획득할 수 있다. 연속적인 시간에서 얻어진 방향각 정보를 확률 기반의 추정을 적용함으로써 잡음 및 반사 파에 강인한 정보를 제공할 수 있는 것이다. 이렇게 획득 된 수중 음원의 방향각 정보는 수중 로봇의 위치 추정이 발산하지 않고 안정적으로 수행될 수 있도록 한다.
본 논문은 다음과 같이 구성된다. 2장은 위치 인식 정 보로 사용될 수중 음원의 방향각 추정 기법에 대해 언급 한다. 3장에서는 관성 센서 정보와 수중 음원의 방향각 정보를 이용한 EKF 기반 SLAM 알고리즘의 수행에 대 해 언급한다. 4장은 실해역에서 수행된 실험 결과를 보 여주며, 마지막으로 5장에서 결론과 함께 향후 연구 방 향에 대해 언급한다.
2. 수중 음원의 방향각 추정
2.1. 목표 신호 추출
수중 음원의 방향각 추정을 위해서는 먼저 수신 하이 드로폰을 통해 획득된 수중 음향 신호 중 방향각 추정의 대상이 되는 음원에서 발생된 신호의 추출이 필요하다. 수중 환경에서의 음향 신호는 음원에서 발생된 신호 외 에도 다양한 잡음 정보가 포함되어 취득된다. 따라서, 안정적인 수중 음원의 방향각 추정을 위해서는 음향 신 호에 존재하는 잡음 정보를 제거하고, 수중 음원에서 발 생된 신호를 추출하는 과정이 필요하다. 만약, 수중 음원 에서 발신된 신호가 아닌 잡음 정보 등을 이용하여 방향 각 추정이 수행된다면 안정적인 방향각 정보가 제공되 지 않을 뿐 아니라, 잘못된 방향각 정보를 이용한 보정으 로 인해 수중 로봇 위치 정보가 발산하게 될 수 있기 때문이다.
언급한 바와 같이, 본 연구에서는 인공 수중 음원을 대상으로 하였고, 해당 음원은 미리 알고 있는 주파수 대역의 음향 신호를 반복적으로 발신한다고 가정하였다. 따라서, 발신 신호의 주파수 대역 정보를 이용하여, 수신 된 수중 음향 신호에 대역통과필터(Band Pass Filter)를 적용함으로써 목표 신호의 추출 및 잡음 정보의 제거를 수행하였다.
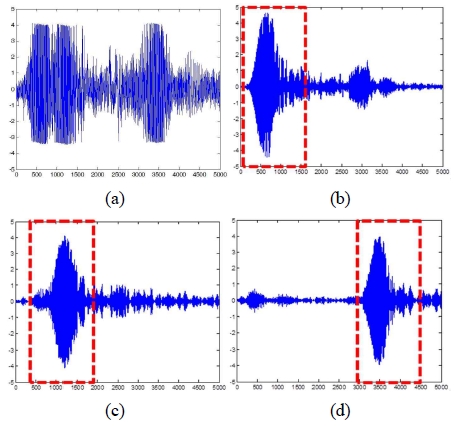
Fig. 1은 대역통과필터를 이용한 목표신호의 추출 과 정을 보여준다. Fig. 1(a)는 세 개의 수중 음원에서 발신 된 신호가 취득된 수중 음향 신호를 보여준다. 그림에서 보이는 바와 같이 다양한 음향 신호가 섞여 있음으로 인해, 개별적인 음원에서 발신되 신호의 추출이 필요함 을 확인할 수 있다. Fig. 1(b)-(d)는 세 종류의 서로 다른 대역통과필터를 통해 잡음정보 제거 및 개별 음원의 발 신 신호만이 필터링된 음향 신호 정보를 확인할 수 있다. 이렇게 얻어진 음향 신호 정보로부터 최종적으로 방향 각 추정에 사용될 목표신호는 음향 신호의 신호 세기를 이용하여 얻어진다. (1)과 같이 대역통과필터가 적용된 후의 음향 신호로부터 신호의 세기가 특정 값 이상이 될 때 목표신호로 추출하는 것이다.M1
| (1) |
여기에서, 은 i번째 대역통과필터를 적용한 신 호의 세기를 나타내며, Eth는 역치값이다. Fig. 1(b)-(d) 에서 붉은색 점선으로 표현된 부분이 최종적으로 추출 된 목표신호를 나타낸다.
2.2. 수중 음원의 방향각 추정
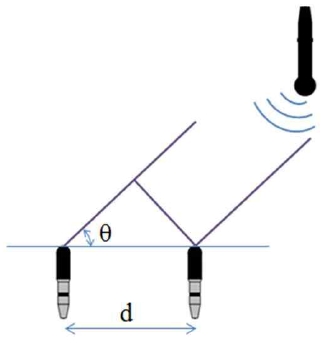
수중 음원의 방향각 추정은 두 개의 하이드로폰으로부 터 수신된 수중 음향 신호의 도달시간지연차로부터 얻어 진다. 서로 다른 하이드로폰이 동일한 음원으로부터 발신 된 음향 신호를 수신할 때, 두 수신신호 간에는 도달시간 지연차(δt )가 존재한다. 이때, 음향신호가 평면파로 전파 되며, 음원과 하이드로폰 사이의 거리가 비교적 멀다고 가정하였을 때, 두 하이드로폰의 도달시간지연은 Fig. 2 와 같이 표현될 수 있다. 또한, 이로부터 음원의 방향각은 다음과 같이 얻어진다.M2M3
| (2) |
| (3) |
여기에서 d는 두 하이드로폰 사이의 거리, C 는 수중 음 속(약 1,500km/s)이다.
위에서 보이는 바와 같이, 음원의 방향각 추정을 위해 서는 도달시간지연의 획득이 매우 중요하다. 도달시간 지연의 획득을 위해서는 상호상관분석, 상호스펙트럼 분석, 빔형성기법, 위상차 추정, 수신 신호를 부분공간 (subspace)으로 변환한 추정 등의 다양한 방법이 사용될 수 있다[12-15]. 본 연구에서는 이러한 방법들 중 가장 많이 사용되는 일반화된 상호상관분석[16,17]을 기반으로 하여 베이지안 프로세스를 적용하였다.
두 수신 음향 신호 s1 (t)과 s2 (t)간의 상호상관분석은 (4)와 같이 두 신호 간의 상호상관(cross-correlation) 값 이 최대가 되는 도달시간지연 값을 추정하는 방법이다.
| (4) |
이러한 상호상관분석은 푸리에 변환을 통해 비교적 쉽게 얻을 수 있다. 또한, 푸리에 변환 과정에서 가중치 함수를 곱해주어 일반화된 상호상관분석이 수행된다.
일반화된 상호상관분석은 비교적 간단한 구현 및 계 산의 정확성으로 인해 다양한 분야에서 활용되어 왔다. 본 연구에서는 이에 더하여 연속적으로 얻어지는 도달 시간지연 정보를 활용하여 베이지안 확률 기반의 방향 각 정보 획득을 수행하였다. 비록 일반화된 상호상관분 석 기법이 간단한 구현과 함께 정확한 도달시간지연을 얻을 수 있으나, 일시적인 잡음 및 반사파 등으로 인해 잘못된 정보를 얻을 수 있기 때문이다.
베이지안 프로세스 기반의 확률적 방향각 추정은 (5) 의 과정을 통해 수행된다.
| (5) |
여기에서 와 는 t시간까지의 일반화된 상호상관 분석 결과 및 모션정보이다. 위의 식은 사전 확률(prior probability)과 우도(likelihood) 확률을 통해 사후 확률 (posterior probability)이 얻어지는 과정을 보여준다. 여 기에서 일반화된 상호상관분석 결과가 likelihood 확률 로써 사용된다. 위의 식으로부터 마코브 과정(Markov process) 가정을 통해 현재 시간에서 얻어지는 도달시간 지연 값에 대한 확률분포를 획득하고, 확률이 최대가 되 는 값으로부터 도달시간지연을 획득한다[18]. 위 식에 대 한 자세한 변수 및 전개는 참고문헌에 언급되어 있다[11].
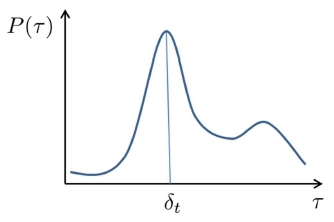
베이지안 프로세스를 통해 얻어지는 posterior 확률 분 포는 Fig. 3과 같이 얻어진다. 이러한 확률 분포로부터, 확률값이 최대가 되는 값을 두 음향 신호 간의 도달시간 지연으로 간주하고, (3)을 이용하여 방향각이 추정된다.
위의 과정을 통해 수행되는 확률적 방향각 추정은 단 지 현재 시간에서 얻어지는 음향 정보로부터 방향각을 추정하는 일반화된 상호상관분석과 달리, 과거에 얻어 진 정보 및 현재 음향 신호 정보를 모두 활용하여 방향각 추정을 수행함으로 인해 잡음 등의 영향을 제거해 줄 수 있다. 일시적으로 잡음 혹은 잘못된 신호 추출로 인해 도달시간지연 값이 왜곡되더라도, 과거의 사전 확률분 포(prior)가 영향을 완화하는 역할을 하기 때문이다.
2.3. 수중 음향 신호 처리 구조
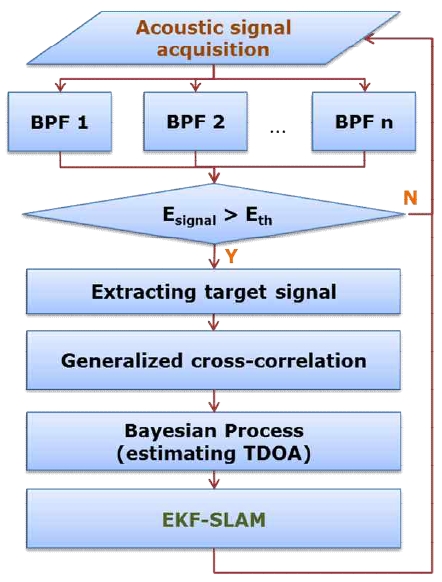
Fig. 4는 제안된 방법의 수중 음향 신호 처리 구조를 순서도 형태로 정리하여 보여준다. 그림에서 보이는 바 와 같이, 취득된 수중 음향 신호는 발신신호의 주파수 정보에 기반한 대역통과필터를 통과하게 된다. 이 과정을 통해 방향각 추정의 대상이 되는 목표 신호 추출 및 발신 음원의 식별(identification)을 수행되게 된다. 또한 방향각 추정을 위해서는 일반화된 상호상관분석 정보와 함께 베 이지안 프로세스 기반의 확률적 방향각 추정 기법이 활용 된다. 이렇게 얻어진 수중 음원의 방향각 정보는 EKF 기반 의 SLAM 알고리즘에 적용되어 수중 음원 및 로봇의 동시 위치 추정에 활용된다.
3. 수중 음원의 방향각을 이용한 EKF SLAM 알고리즘
수중 음향 신호로부터 추정된 음원의 방향각 정보는 EKF 기반의 SLAM 알고리즘에 적용된다. EKF-SLAM 은 예측 과정과 보정 과정으로 구성된다. 예측 과정은 직전 상태 정보와 제어 입력(control input)을 활용하여 현재의 상태를 추정하는 과정이고, 보정 과정에서는 외 부 센서 정보를 이용하여 예측된 상태 정보를 보정한다. 이를 위해, 본 연구에서는 관성 센서 정보와 수중 음원의 방향각 정보가 함께 활용되어 안정적인 수중 음원 및 로봇에 대한 위치 인식을 수행하게 된다.
3.1. 관성항법 정보 획득
제안된 EKF-SLAM 기법에서는 예측 과정을 위해 관성 센서 정보를 활용한다. 수중 로봇에서 주로 사용되는 관성 측정장치(Inertial Measurement Unit, IMU)와 도플러속도 계(Doppler Velocity Log, DVL) 기반의 관성항법 정보를 통해 해당 과정이 수행된다. 즉, IMU와 DVL 센서의 융합 을 통해 얻어지는 추측항법(dead-reckoning) 정보를 EKFSLAM 알고리즘에서의 예측 정보로 활용하게 된다.
EKF-SLAM을 위한 상태 벡터는 다음과 같이 정의된다.M6
| (6) |
여기에서 Xυ는 수중 로봇의 상태 정보이며, Xs는 수중 음원에 대한 위치 정보이다. 위의 상태 벡터에 대한 공분 산 행렬은 다음과 같이 정의된다.M7
| (7) |
수중 로봇의 위치 추정을 위한 상태 벡터는 다음과 같이 정의된다.M8
| (8) |
여기에서 x, y, s는 수중 로봇의 위치 정보이며, φ, θ, ψ는 자세 정보이다. 또한, u, v, w는 로봇 좌표계 상에서의 속 도 정보이다. 본 연구에서는 하이드로폰이 두 개만 장착 된 로봇 시스템을 대상으로 함에 따라, 실제적으로 2차 원에 대한 위치 추정을 수행한다. 하지만, 일반적인 수중 로봇 시스템으로의 확장성을 고려하여 3차원에 대한 상 태 정보를 모두 활용하였다.
예측 과정에서는 직전 단계의 상태 벡터와 IMU와 DVL 센서 정보를 활용하여 현재 단계에서의 상태 벡터 를 획득한다.M9
| (9) |
여기에서 ut는 IMU와 DVL센서로부터 얻어지는 수중 로봇에 대한 제어 입력값이다.
3.2. 수중 음원의 방향각 정보 활용
언급한 바와 같이, 제안된 수중 로봇의 위치 추정 기법 은 수중 로봇의 EKF-SLAM을 수행하기 위해 수중 음원 을 랜드마크로 사용한다. 이를 위해, 수중 음원의 위치 위치 추정을 위한 상태 벡터는 다음과 같이 정의된다.M10
| (10) |
여기에서 는 i번째 수중 음원에 대한 2차원 위치 정보를 의미하며, n은 사용된 수중 음원의 개수이다.
두 개의 하이드로폰을 이용한 수중 음향 신호 처리는 음원에 대한 방향각 정보만을 제공한다. 따라서, 수중 음원 위치의 초기화를 위해서는 거리값이 필요하다. 본 연구에서는 수중 음원의 측정 가능 거리를 기반으로 하 여, 임의의 초기 거리 값과 함께 거리 방향으로의 분산값 을 크게 설정하는 방식으로 초기화를 수행하였다.
EKF-SLAM을 위한 측정값은 (11)과 같이, 음원에 대한 방향각 정보이다.
| (11) |
여기에서 는 t시간에 얻어진 i번째 음원에 대한 방 향각 정보이다.
이로부터 얻어지는 측정모델은 (12)와 같다.
| (12) |
수중 음원으로부터 얻어진 방향각 정보는 위의 측정 모델을 통해 EKF-SLAM에 적용되어, 수중 로봇의 위치 정보와 함께 수중 음원의 위치를 동시에 추정하는데 사 용된다. (11)과 (12)의 측정값 및 측정모델을 이용하여 상태벡터와 공분산행렬의 보정은 (13)-(15)의 식으로부 터 수행된다.M14
| (13) |
| (14) |
| (15) |
여기에서 K(t)는 칼만 게인, H(T)는 측정모델의 Jacobian 행렬, Q(t)는 측정값에 대한 공분산행렬이다.
위의 과정을 통해 수행되는 제안된 방법은 수중 음원 의 방향각 정보와 관성 센서 정보를 EKF-SLAM 기법에 적용함으로써, 수중 로봇의 안정적인 위치 추정에 적용 될 수 있다.
4. 실험 결과
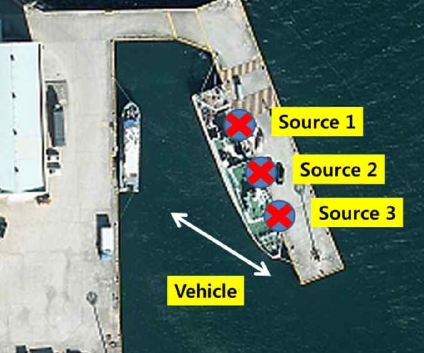
제안된 수중 음원 기반의 로봇 위치 추정 기법의 검증 을 위해, 한국해양과학기술원 남해연구소 내의 부두 환 경에서 실해역 실험을 수행하였다. 제안된 방법은 수중 로봇의 위치 추정을 위해 개발되었으나, 두 개의 하이드 로폰이 장착된 로봇 시스템의 한계로 인해 2차원 위치 추정을 수행한다. 따라서, 실험의 편의성, 그리고 성능 검증을 위해 DGPS를 이용한 절대 위치 획득의 이유로 무인 수상선을 활용한 실험을 수행하였다(Fig. 5).
수중 음향 신호의 취득을 위해 장착된 하이드로폰은 B&K 8103 모델을 이용하였으며, Fig. 5에서 빨간색 원 으로 표시되어 있다. 그림에서 보이는 바와 같이 로봇 시스템에는 두 개의 하이드로폰이 장착되어, 수중 음향 신호를 취득하고 수중 음원의 방향각 정보를 획득할 수 있도록 하였다. 수중 음향신호는 100 kHz의 속도로 취득 되었다. 관성 센서 정보 획득을 위해서는 IMU와 DVL 센서가 장착되었으며, 추정된 위치의 정확성 분석을 위 한 절대 위치 값 획득을 위해 DGPS가 장착되었다. IMU 는 Microstain사의 3DM-GX3 모델을 사용하였으며, 10 ms의 주기로 3축의 각가속도와 각속도 정보가 취득되었 다. 이에 대한 분산값은 0.12 (m/s2)2, 0.012 (rad/s)2가 사용 되었다. DVL은 Teledyne RDI사의 Explorer 모델이 사용 되었으며, 200 ms의 주기로 3축의 속도 정보가 취득되었 다. 이에 대한 분산값은 0.0052 (m/s)2가 사용되었다.
Fig. 6은 실험이 수행된 위치에서의 항공사진과 함께 설치된 수중 음원의 위치와 로봇의 이동 경로를 보여준 다. 실제 실험은 음원의 설치, 로봇의 이동을 고려하여 항공사진에서 보이는 두 척의 선박들이 정박되지 않은 상황에서 수행되었다. 그림에서 보이는 바와 같이 총 3개 의 수중 음원이 사용되었으며, 각각의 음원은 미리 정해 둔 서로 다른 주파수 대역의 신호를 100 ms의 주기로 반복적으로 발신하도록 하였다. 로봇 시스템은 수중 음원 의 방향각 정보 취득 및 위치 추정 수행을 위해, 경로의 왼쪽 상단 위치에서 출발하여 오른쪽 하단으로 이동 후 다시 왼쪽 상단의 위치로 돌아왔다.
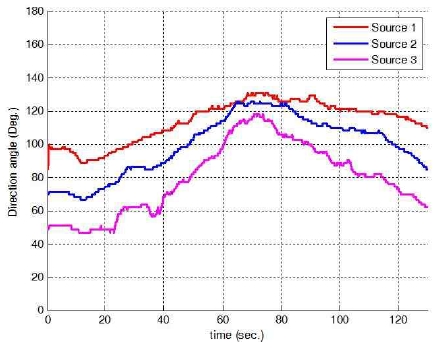
Fig. 7은 추정된 수중 음원의 방향각 정보이다. 언급한 바와 같이 음향신호가 100 ms의 주기로 발신됨에 따라, 로봇은 10 Hz의 속도로 방향각 추정을 수행하였다. 방향 각 추정 결과를 보면, 로봇이 경로의 오른쪽 아래로 이동 함에 따라 방향각이 증가하였고, 다시 경로의 왼쪽 상단 으로 이동함에 따라 방향각 정보가 감소하는 경향을 확 인할 수 있다. 이러한 방향각 정보는 EKF-SLAM을 수행 하기 위해 측정값으로 사용되었으며, 이에 대한 분산값 은 152 deg.가 사용되었다.
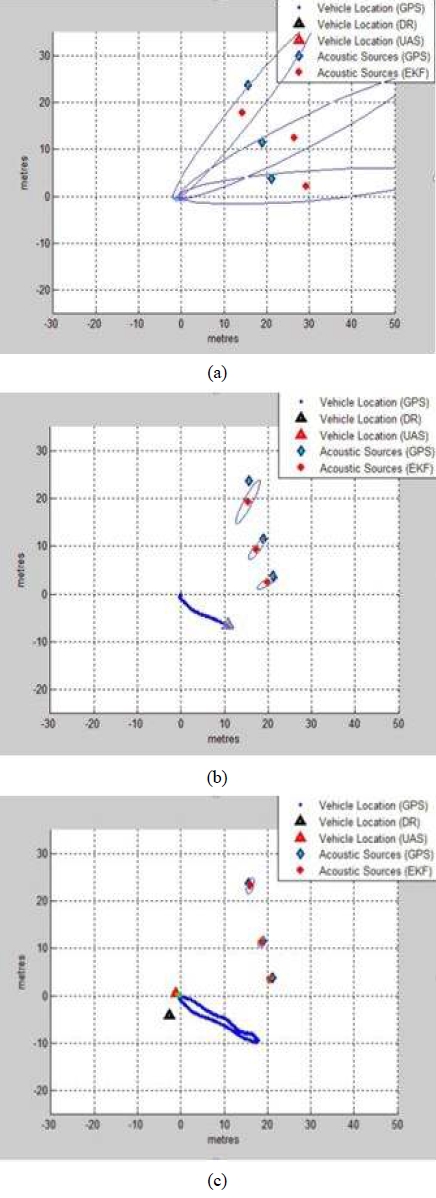
Fig. 8은 3개의 수중 음원을 이용해 EKF-SLAM을 수 행한 결과이다. 그림에서 빨간색 삼각형은 추정된 로봇 의 위치이며, 검은색 삼각형은 관성 센서만을 통해 얻어 진 로봇 위치이다. 또한, 빨간색 십자가는 추정된 수중 음원의 위치이며, 파란색 타원은 이에 해당하는 공분산 을 표현한 것이다. 파란색 점들은 DGPS로부터 얻어진 로봇의 실제 경로, 하늘색 다이아몬드는 수중 음원의 실 제 위치이다.
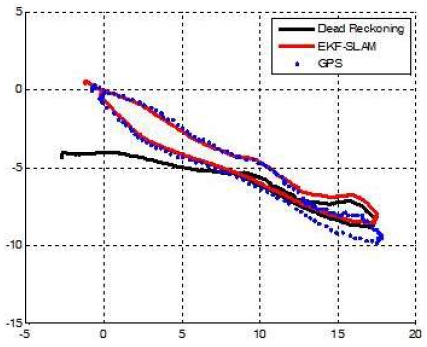
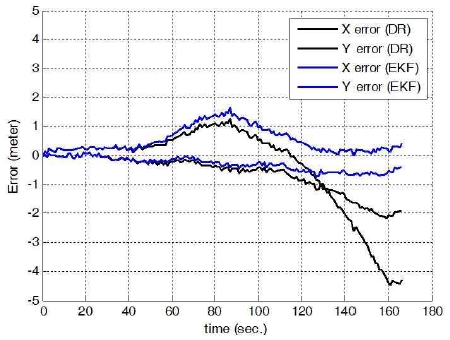
Fig. 8(a)에서 보이는 바와 같이, 수중 음원에 대한 위 치는 상당히 큰 거리 불확실성을 가지며 초기화되었다. 하지만 Fig. 8(b)-(c)와 같이 로봇이 이동함에 따라 음원 위치에 대한 불확실성이 줄어들며, 실제 음원의 위치에 수렴해가는 것을 확인할 수 있다. Fig. 9는 추정된 로봇 위치에 대한 결과를 보여준다. 이에 대한 오차는 Fig. 10에서 보여진다. 그림에서 보이는 바와 같이 관성 센서 정보만을 통해 얻어진 결과는 시간이 지남에 따라 위치 오차가 누적되어 발산하는 것을 확인할 수 있다. 반면, 추정된 위치는 오차가 한정적으로 유지되는 것을 확인 할 수 있다.
Table 1은 추정된 수중 음원의 위치 정보와 DGPS로 부터 얻어진 참값과의 오차를 보여준다. Table 1에서 보 이는 바와 같이, 세 개의 수중 음원에 대해 최대 0.6 m 이내의 위치 오차를 가지며 추정되었다.
실험 결과에서 얻어진 로봇과 음원의 위치 추정 결과 에 대한 오차 원인은 다음과 같이 분석될 수 있다. 먼저, 수중 잡음 및 반사파에 의한 방향각 정보의 오차이다. 비록 제안된 방법이 확률적 방향각 추정을 통해 잡음 및 반사파에 대해 강인하도록 개발되었으나, 이에 대한 영향이 지속적으로 나타나는 구간에 대해서는 방향각 정보의 오차가 존재할 수 있다. 다음으로, 방향각 추정의 정밀도의 한계로 인한 오차이다. 방향각 추정의 정밀도 는 음향 신호 취득 속도에 의한 한계가 결정된다. 도달시 간지연이 취득 속도의 배수로 결정되기 때문이다. 마지 막으로, 해당 기법이 방향각 정보 만을 이용한 보정을 수행함으로 인해, 보정의 한계성이 존재한다. 수중 음원 에 대한 거리 정보가 제공되지 않음으로 인해 거리 방향 으로의 보정에 한계가 있고, 이로 인한 오차가 발생한 것으로 분석된다.
로봇 및 음원에 대한 위치 오차의 절대값은 실험 방법, 로봇의 이동 경로 등에 따라 달라질 수 있다. 하지만, 제안된 방법은 위치 오차가 발산하지 않고 한정적으로 유지될 수 있도록 하여 수중 로봇의 안정적인 2차원 위 치 추정에 활용될 수 있음을 실험적으로 검증되었다.
5. 결론 및 향후계획
본 논문에서는 수중 음원의 방향각 정보를 활용한 수 중 로봇의 2차원 위치 추정 기법을 제안하였다. 대역통 과필터를 이용한 잡음 제거 및 음원의 방향각 정보 추정 에 사용될 목표 신호 추출을 수행하였다. 추출된 목표 신호는 일반화된 상호상관분석과 함께, 베이지안 확률 기반의 방향각 추정을 수행함으로써 반사파 혹은 일시 적인 잡음 등의 정보에도 안정적인 방향각이 추정되도 록 하였다. 이렇게 얻어진 방향각 정보는 EKF 기반의 SLAM에 적용되어 사전 정보 없이 수중 로봇 및 음원의 2차원 위치 추정을 성공적으로 수행할 수 있었다. 제안 된 방법은 베이스라인 기반의 위치 추정 시스템들과 달 리, 사전 정보가 필요하지 않고, 음원의 설치 및 위치 보정 등의 과정이 필요하지 않다는 점에서 효과적이고 편리한 수중 로봇의 위치 추정 기법을 제공할 수 있다는 장점이 있다.
향후 계획으로는 두 개의 하이드로폰으로 수행되던 2차원 방향각 추정을 다 수의 하이드로폰을 사용하여 3차원으로 확장하고 이를 통해 수중 로봇 및 음원의 3차 원 위치 추정에 적용할 것이다.
Acknowledgments
This research was supported by the projects, “Development of basic SLAM technologies for autonomous underwater robot and software environment for MOOS-IvP” sponsored by Korea Research Institute of Ships \& Ocean engineering (KRISO) and “Development of an autonomous swimming technology with less than 1.0m position error for underwater robot operating in man-made structural environment” sponsored by Ministry of Trade, Industry \& Energy (MOTIE).
References
-
Whitcomb, L, Yoerger, D, Singh, H, Howland, J, “Advances in underwater robot vehicles for deep ocean exploration: Navigation, control and survey operations”, in Proc. of The Ninth International Symposium on Robotics Research, (1999), p346-353.
[https://doi.org/10.1007/978-1-4471-0765-1_53]

-
Kim, A, Eustice, R M, “Real-time visual SLAM for autonomous underwater hull inspection using visual saliency”, IEEE Transactions on Robotics, (2013), 29(3), p719-733.
[https://doi.org/10.1109/tro.2012.2235699]

-
Lee, Y, Choi, J, Choi, H T, “Underwater robot localization by probability-based object recognition framework using sonar image”, Journal of Korea Robotics Society, (2014), 9(4), p232-241.
[https://doi.org/10.7746/jkros.2014.9.4.232]

-
Choi, HT, Kim, SM, Byun, SH, Kim, K, “Development of underwater Robot & Underwater acoustic signal recognition system”, in Proc. of the Conference on Information and Control Systems, (2010), p53-54.
[https://doi.org/]

-
Kim, TG, Ko, NY, “Localization of an underwater robot using acoustic signal”, Journal of Korea Robotics Society, (2012), 7(4), p270-274.
[https://doi.org/10.7746/jkros.2012.7.4.231]

-
Vickery, K, “Acoustic positioning systems. A practical overview of current systems”, in Proc. of the 1998 Workshop on Autonomous Underwater Vehicles, (1998), p5-17.
[https://doi.org/10.1109/auv.1998.744434]

-
Alcocer, A, Oliveira, P, Pascoal, A, “Underwater Acoustic Positioning Systems based on Buoys with GPS”, in Proceedings of the Eighth European Conference on Underwater Acoustics, (2006).
[https://doi.org/]

-
Kinsey, JC, Eustice, RM, Whitcomb, LL, “A survey of underwater vehicle navigation: Recent advances and new challenges”, Proc. 7th IFAC Conf. Manoeuvring Control Mar. Craft, (2006).
[https://doi.org/]

-
Newman, P, Leonard, J, “Pure range-only sub-sea SLAM”, in Proc of the International Conference on Robotics and Automation, (2003), p1921-1926.
[https://doi.org/10.1109/robot.2003.1241875]

-
Eustice, RM, Whitcomb, LL, Singh, H, Grund, M, “Recent advances in synchronous-clock one-way-travel-time acoustic navigation”, in Proc. of IEEE/MTS OCEANS, (2006).
[https://doi.org/10.1109/oceans.2006.306931]

-
Choi, J, Choi, HT, “Underwater acoustic source localization based on the probabilistic estimation of direction angle”, Journal of Korea Robotics Society, (2014), 9(4), p206-215.
[https://doi.org/10.7746/jkros.2014.9.4.206]

-
Ahmed, HI, Wei, P, Memon, I, Du, Y, Xie, W, “Estimation of time difference of arrival (TDOA) for the source radiates BPSK signal”, International Journal of Computer Science Issues, (2013), 10(Issue 3), no. 2p163-171.
[https://doi.org/]

-
Ahn, BK, Go, YJ, Wook, Rhee, Choi, JS, Lee, CS, “Localization of underwater noise sources using TDOA (Time Difference of Arrival) method”, Journal of the Society of Naval Architects of Korea, (2011), 48(2), p121-127.
[https://doi.org/10.3744/snak.2011.48.2.121]

-
Smith, KB, Kouteas, SD, Therrien, CW, “Underwater Target Tracking Using Signal Subspace TDOA and Differential Doppler”, Annual Conference of the Australian Acoustical Society, (2002).
[https://doi.org/]

-
Shimoyama, R, Yamazaki, K, “Acoustic source localization using phase difference spectrum images”, Acoustic Science and Technology, (2003), 24(4), p161-171.
[https://doi.org/10.1250/ast.24.161]

-
Knapp, CH, Carter, GC, “The generalized correlation method for estimation of time delay”, IEEE Transaction on Acoustics, Speech, and Signal processing, (1976), 24(4), p320-327.
[https://doi.org/10.1109/tassp.1976.1162830]

-
Park, PB, Ban, KD, Kwak, KC, Yoon, HS, “Performance analysis of GCC-PHAT-based sound source localization for intelligent robots”, Journal of Korea Robotics Society, (2007), 2(3), p270-274.
[https://doi.org/]

-
Thrun, S, Burgard, W, Fox, D, Probabilistic Robotics, (2005), MIT Press, Cambridge, MA.
[https://doi.org/]

2003 포항공과대학교 기계공학과(학사)
2005 포항공과대학교 기계공학과(석사)
2011 포항공과대학교 기계공학과(박사)
2013 ~ 현재 한국해양과학기술원 부설 선박 해양플랜트연구소 해양시스템연구부 선임연구원
관심분야: 수중 로봇, 위치인식, SLAM
2009 충남대학교 메카트로닉스공학과(학사)
2014 충남대학교 메카트로닉스공학과(석사)
2011 ~ 현재 한국해양과학기술원 부설 선박 해양플랜트연구소 해양시스템연구부 연구원
관심분야: 수중 로봇, 영상처리, 영상소나