전자기파의 감쇠패턴 및 깊이 정보 취득을 이용한 수중 위치추정 기법

1. 서 론

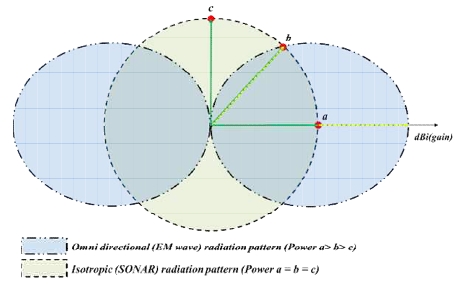
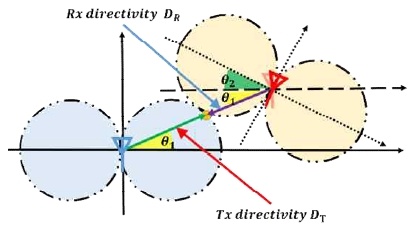
최근 해양 공간 개발을 통한 화석연료의 확보, 희소가 치가 높은 광물 채집 등의 자원 개발과 군사적 용도 의 수중 공간 활용이 활발하게 이루어지고 있다^[1]. 얕은 수 심의 근해에서는 사람을 통한 작업이 일부 이루어지고 있지만 오랜 시간 작업 또는 깊은 수심에서의 작업을 위해서는 특수 감압 장비에 의존하지 않는 한 사람이 작업하는 것은 매우 어렵다^[2]. 이를 해결하기 위해 1980 년대 이후로 수중 작업용 로봇의 개발이 활발히 이루어 지고 있으며^[3], 사람이 개입하여 원격으로 작업을 수행 하기 위한 원격 조종잠수정인 ROV (Remote Operated Vehicle)와 주어진 임무를 사람의 개입 없이 자율적으로 수행하는 자율구동잠수정인 AUV (Autonomous Unmanned Vehicle)가 활용되고 있다. 이러한 수중 로봇을 통해 원 하는 목적을 원활하게 달성하기 위해서는 무엇보다 정 확한 수중 위치 인식이 필수적이다. 수중 환경에서 가장 널리 이용되고 있는 수중 위치 추정 방식은 초음파를 활용하는 방법들이다^[4]. 초음파는 공기 중 대비 수중 환 경에서 빠른 속도와 전달 성능이 좋기 때문에 넓은 영역 에 대한 위치 추정 솔루션이 많이 개발되어 있으며 대부 분의 수중 이동체(로봇, 잠수함, 선박)들은 이를 이용하 여 위치 정보를 획득한다. 이외에도 초음파 영상을 통한 기법^[5], 자기장을 통한 기법^[6], 전자기파를 이용한 기법^[7] 등이 개발된 바 있으며 제한적인 환경에서 사용되고 있 다. 이러한 방법들 중 전자기파를 이용한 수중 위치 추정 기법은 전자기파의 거리에 따른 감쇠를 이용하여 거리 를 추정하는 방법으로 10 m 이내의 근거리에서 수 cm 위치 추정이 가능하여 근접하여 작업을 수행하는 경우 에 정밀한 위치 추정 성능을 제공할 수 있다는 장점을 가지고 있다. 하지만 3차원 공간 상에서는 위치추정에 있어 오차가 발생할 수 있는데, 이는 전자기파의 방사패 턴의 형상에 기인한 것으로 Fig. 1의 초록색 형상과 같이 이상적인 구형 방사패턴을 가지는 안테나가 존재할 경 우 동일한 반경 내에서 얻어지는 감쇠 데이터가 같지만 일반적으로 가장 널리 사용되는 등방형 안테나의 실제 방사패턴은 파란색 영역과 같은 도넛 형상을 가지고 있 기 때문이다. 이런 경우 동일한 거리에서 동일한 신호 세기를 얻을 수가 없기 때문에 동일한 반경에서의 수신 되는 신호세기의 차이가 발생한다^[8].

Fig. 1

EM wave radiation pattern

이를 보완하기 위해 본 논문에서는 수중에서 깊이 정 보를 정확하게 측정할 수 있는 압력센서를 이용하여 깊 이에 대한 데이터를 추가 활용하는 방법을 제안한다. 압 력센서에 의해 얻어진 깊이 정보를 통해 깊이 방향 좌표 값인 z값이 고정된 평면 상에서 x와 y위치에 대한 추정을 진행할 수 있다. 이러한 과정을 통해 감쇠패턴 모델을 활용한 위치 추정 기법이 단순화되고 보다 빠르고 정밀 한 위치추정을 수행할 수 있다. 이를 위해 본 논문에서는 초소형기전공학(MEMS) 기반 압력센서를 선정하여 수 중에 위치시키고 깊이에 따른 변화를 실제 깊이와 비교 한 모델을 구하고, 기존 3차원 전자기파 감쇠 패턴 모델 에 압력센서 데이터(깊이 데이터 z)를 추가하여 특정 지 점의 위치 추정을 진행하고 이에 따른 오차를 분석한다.

2. 전자기파를 이용한 위치추정 기법

일반적으로 공간 상에서 고정된 여러 노드들로부터의 거리를 측정하여 위치를 추정하는 기법을 활용하기 위 해 주로 사용하는 전달 신호의 도달시간(TOA: Time Of Arrival) 또는 도달각도(AOA: Angle Of Arrival) 측정 등의 방법^[9]을 통해 개별 거리를 유추하여 사용하는데, 앞서 설명한 초음파를 활용한 위치 추정에서도 대부분 이와 같은 방법들이 사용된다. 반면 전자기파를 이용한 위치추정 기법에서는 수중 거리에 따른 전자기파 신호 감쇠(signal attenuation) 정도에 따른 거리 추정 방법을 사용한다. 이 방법은 송신된 전자기파의 신호 세기 대비 수신된 신호세기의 차이를 이용하여 거리를 유추하는 방식으로 도달시간 측정 방법과는 다르게 신호 왕복 이 동을 요구하지 않으며, 도달시간 측정 방법에서 필수적 인 시간 동기화가 필요 없다는 장점이 있다. 이렇게 얻어 진 다수의 알려진 고정 노드(fixed node)의 위치와 움직 이는 모바일 노드(mobile node)간의 거리 데이터들을 이 용하여 위치를 추정한다.

2.1. 전자기파를 이용한 수중 감쇠 모델

수중 전자기파 위치추정 기법에 사용되는 신호감쇠 기반 거리 추정 모델은 매질의 특성에 따른 평면파(plane wave) 방정식과^[10] 안테나의 패턴에 따른 FRIIS 방정식이 다^[11]. 먼저 매질에 따른 감쇠 특성은 J. C. Maxwell^[10,12] 에 의해 제안된 수식 (1)과 같이 감쇠상수 α에 따라 거리 R에 대해서 감쇠하는 경향을 보여준다.

$\[ \frac{P_R}{P_T}=\text{exp}\left(-\alpha R\right) \]$

(1)

여기서 P_T는 송신 에너지, P_R은 수신 에너지를 의미하 고, 감쇠상수 α는 도전율 σ, 투자율 μ, 유전율 ε에 의해 영향을 받는다. 또한 전자기파는 안테나의 특성에 따라 신호감쇠를 보여주는데 이는 FRIIS 방정식에 따라 수식 (2)와 같이 정의된다.

$\[ \frac{P_R}{P_T}=\frac{{\lambda }^2}{{\left(4\pi R\right)}^2}{G}_T{G}_R\left(PLF\right) \]$

(2)

이 모델은 송수신 안테나의 성능을 나타내는 이득 G_T , G_R전자기파의 파장 λ, 송수신 안테나 사이의 거리 R , 편향손실인자(PLF: Polarization Loss Factor) 그리고 송 수신전파의 세기 P_T , P_R로 구성된다. 앞선 두 식은 매질 과 안테나의 특성에 따른 독립 모델로서 주로 공기 중에 서 매질 변수를 1에 근접하게 적용한다. 하지만 수중 환 경에서는 두 모델 모두 영향을 주므로 수식 (3)과 같이 매질의 영향을 고려한 신호감쇠 모델이 제안된 바 있다 ^[7,8,13].

$\[ \frac{P_R}{P_T}=\frac{{\lambda }^2}{{\left(4\pi R\right)}^2}{G}_T{G}_R\left(PLF\right)\times \text{exp}\left(-\alpha R\right) \]$

(3)

수식 (3)을 통해 고정된 노드와 모바일 노드간의 거리데 이터 R를 얻고 여러 노드에서 방사된 신호를 획득하여 각 노드간의 거리데이터와, 삼각측량법을 이용하면 Fig. 2 과 같이 수중 전자기파를 활용한 위치 추정이 가능하다^[14].

Fig. 2

Planer localization result with 4 signal attenuation data

2.2. 안테나의 이득패턴에 따른 신호 감쇠 경향

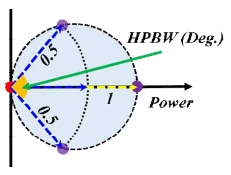
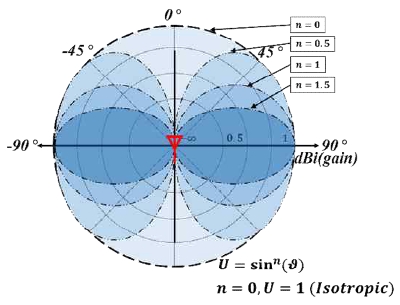
하지만 3차원 공간에서의 전자기파 신호 감쇠 기반 수중 위치 추정을 위해서는 수식(3)에 추가적으로 고려 해야 하는 부분이 안테나의 감쇠 패턴 형상에 영향을 주는 이득(G_T ,G_R )인데, 이는 Fig. 3 같이 최대 전력의 절반이 측정되는 각도인 반전력빔폭(half power beam width: HPBW)과 Fig. 4의 안테나의 지향성 패턴 결정인 자 n를 이용하여 안테나의 이득을 수식 (4)와 같이 표현 할 수 있다^[13].

Fig. 3

Half power beam width

Fig. 4

Directivity characteristics according to “n”

수식 (4)는 수식 (3)의 안테나 이득 부분을 구체화한 모델로서, 이를 통해 Fig. 5와 같이 안테나의 상대 자세 (위치각 θθ₁, 자세각 θθ₂)^[13]에 따른 신호감쇠를 표현할 수 있다.

Fig. 5

Directivity angle according to elevation and inclination mismatch

$\[ G_T{G}_R=e_T{e}_R{D}_{Tmax}{\text{cos}}^{nT}\left({\theta }_1\right)D_{Rmax}{\text{cos}}^{nR}\left({\theta }_1,{\theta }_2\right) \]$

(4)

수식 (4)와 같이 정의된 안테나의 이득은 모델을 활용 하여 이론적으로 다수의 고정 노드와 모바일 노드간의 데이터로 위치 추정이 가능하다. 하지만 모바일 노드의 위치가 고정 노드 대비 자세 불일치 정도가 심할 경우 위치를 추정하지 못하거나, 추정하는데 많은 시간이 요 구되기도 한다. 이런 문제를 해결하기 위해 3절에서는 압력 센서를 이용하여 수직 위치를 보정하기 위해 깊이 에 따른 모델을 구하고, 깊이 데이터를 반영한 위치 추정 을 진행하였다.

3. 위치 추정 정보의 취득 및 추정시스템

3.1. 수중 3차원 위치정보의 취득 방법

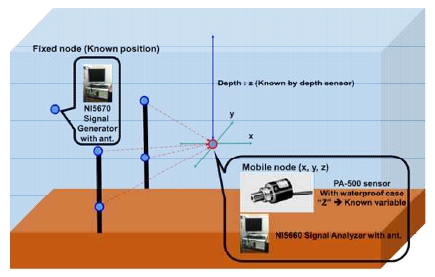
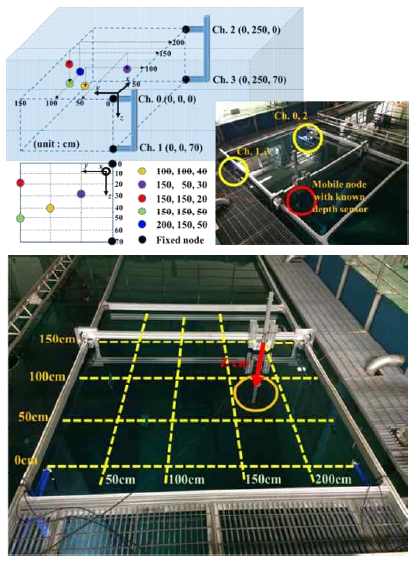
전자기파를 이용한 3차원 수중 위치 추정을 위해 깊이 정보를 취득할 수 있는 압력센서를 모바일 노드에 부착 하여 Fig. 6과 같이 안테나와 센서를 수직으로 이동 시키 면서 실험을 진행하였다.

Fig. 6

Conceptual localization diagram using EM wave with depth information

먼저 Fig. 6의 고정 노드는 National Instrument^TM 사의 NI5670 신호 발생기(signal generator)를 이용하여 일정 한 세기(10 dBm)로 신호를 방사하고 모바일 노드는 NI5660 신호 분석기(signal analyzer)를 이용하여 각 채널(4개의 개별 노드) 별로 들어온 데이터를 수신하여 위치를 추정 하였다. 측정된 신호감쇠 데이터에 압력센서로부터 얻 어진 깊이 정보를 적용하여 3차원 위치에 대해 추정을 진행하였다.

3.2. 압력센서 보정 위치 추정 기법 실험 및 결과

임의의 측정점에 모바일 노드를 위치시키고 4개 고정 노드로부터 방사되는 전자기파의 신호 감쇠 데이터들을 측정한 뒤 측정된 데이터에 압력센서로부터 얻어진 깊 이 z값을 적용하여 실제 평면에서의 위치 x, y를 파악하 여 3차원 위치를 추정하였다.

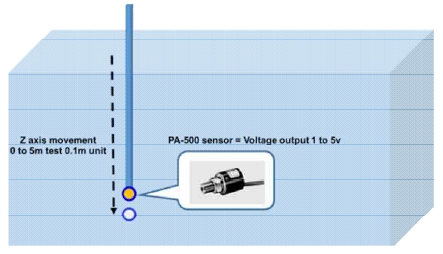
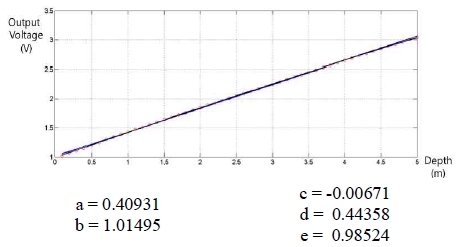
먼저 압력센서를 활용한 압력 대비 거리 모델을 Fig. 7과 같이 실험을 수행하여 수식 (5)와 같이 구하였다.

Fig. 7

Pressure sensor experiment

$\[ Z_{depth}\left(m\right)=0.098x_{volt}^2+{2.04}_{volt}-2.10 \]$

(5)

수식 (5)는 수식 (6)의 1차 선형(Line) 방정식과 수식 (7)의 2차 방정식을 사용하고 최소제곱법을 이용하여 Fig. 8의 변수들을 이용 근사화를 진행하여 도출하였다.

Fig. 8

Data fitting result

$\[ Z_{depth}\left(m\right)=\frac{x_{volt}-b}{a} \]$

(6)

$\[ Z_{depth}\left(m\right)=\sqrt{\frac{x_{volt}-e}{c}-\frac{d^2}{4c^2}}-\frac{d}{2c} \]$

(7)

압력센서 모델로 추정된 전압 값과 실제 측정된 전압 값 간의 차이를 Table 1에 나타내었으며 이들 두 값의 상관계수인 R²값은 0.9953으로 나타났으며 이는 모델 에 의해 추정된 값을 실측 값으로 사용할 수 있음을 나타 낸다.

Table 1

Pressure sensor model data

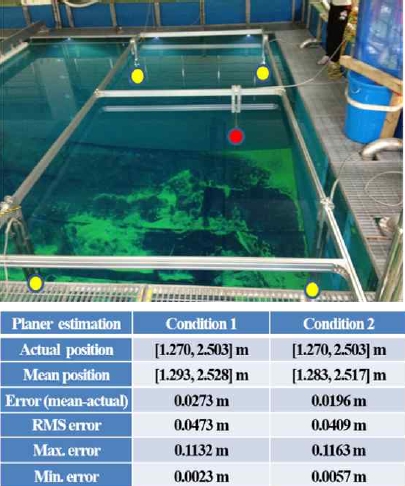
제안한 방법의 유효성을 엄밀하게 검증하기 위해서는 잠수정에 모바일 노드를 장착해서 검증하여야 하나 수 중 환경의 특성상 잠수정에 장착했을 경우 정확한 실측 검증(ground truth) 데이터 획득이 어렵기 때문에 알려진 3차원 지점에서 오차를 검증하는 것이 좋은 방법이라고 판단된다.

위치 추정 실험은 Fig. 9와 같이 총 5개의 위치를 지정 하여 압력센서를 포함한 모바일 노드를 위치시키고, 지 정된 위치에서 압력센서에서 얻어진 전압 값을 수식 (5) 를 통해 깊이 값으로 변환하고 실제 위치 대비 전자기파 와 압력센서를 통해 얻은 결과를 비교 분석하였다. 지정 된 위치의 노드를 통해 얻은 결과와 실험 값을 비교한 결과를 Table 2에 나타내었다. 각 노드에서 전자기파를 통해 얻은 값의 평균을 실험 데이터로 두고 수식 (5)를 통해 얻은 전압 값을 적용하여 실제 위치와 추정된 위치 의 에러의 평균을 이용하여 실제 위치 대비 실험 값의 위치 오차를 구하였다. 또한 압력센서의 유무에 따른 실 험오차의 차이를 비교하여 압력센서가 없는 모델 대비 다소 오차가 줄어든 것을 확인할 수 있다. 이 결과로 절 대 깊이를 확인할 수 있는 압력센서를 가지고 기존 위치 추정 결과를 보정하여 보다 정밀한 위치추정 결과를 얻 어낼 수 있음을 확인하였다.

Fig. 9

Experimental environment

Table 2

The position error result

위치 추정 결과로 제시한 지점들은 안테나의 방사패 턴을 다양하게 살펴볼 수 있는 위치로 제안한 방법으로 모든 영역에서 고르게 향상된 위치 추정 결과를 얻을 수 있었다.

4. 결 론

본 논문은 전자기파의 3차원 감쇠패턴을 이용한 수중 위치추정 방법을 보완하기 위해 압력센서를 적용하여 위치 추정 정밀도와 효율을 높이기 위한 방법을 제안하 였다. 압력센서의 수중 실험을 통해 센서데이터의 안정 성을 확인하고 깊이에 따른 모델을 구하였고, 이를 3차 원 전자기파 신호감쇠 모델의 깊이 z값에 적용하였다. 이 결과 추정 오차가 감소하는 것을 확인하였고, 기존 전자기파의 감쇠 패턴만을 사용한 위치 추정 대비 얻어 지는 데이터의 안정성이 증가하는 것을 확인하였다. 또 한 기존 3변수 x, y, z를 추정하지 않고 2변수 x, y만을 추정하게 되어 연산속도 역시 상승함을 확인할 수 있었 다. 이를 통해 향후 추정 알고리즘의 개량과 센서 모듈의 실시간 데이터 획득 방법을 개발하여 실제 로봇의 움직 임에 따른 실시간 위치 추정에 적용할 수 있을 것이다.

Acknowledgments

This research was a part of the project titled ‘Development of small drag bio-mimetic underwater robots’, funded by the Ministry of Oceans and Fisheries, Korea

References

• Langdon, M, “Deep impressions”, Engineering and Technology, (2010, May), 5(7), p40-43. [http://dx.doi.org/10.1049/et.2010.0708]
• Anonymous, “US Navy Sets New Diving Record with Ocean Works Atmospheric Diving”, Ocean News and Technology, (2006), 12(5), p10. [https://doi.org/]
• Paull, L, Saeedi, S, Seto, M, Li, H, “AUV navigation and localiza- tion: A review”, Oceanic Engineering, (2014), 39(1), p131-149. [http://dx.doi.org/10.1109/JOE.2013.2278891]
• Kim, T G, Ko, N Y, “Localization of an Underwater Robot Using Acoustic Signal”, The Journal of Korea Robotics Society, (2012, Dec), 7(4), p231-242. [https://doi.org/10.7746/jkros.2012.7.4.231]
• Lee, Y, Choi, J, Choi, H, “Underwater Robot Localization by Probability-based Object Recognition Framework Using Sonar Image”, The Journal of Korea Robotics Society, (2014, Dec), 9(4), p232-241. [https://doi.org/10.7746/jkros.2014.9.4.232]
• Akyildiz, I F, Wang, P, Sun, Z, “Realizing underwater communication through magnetic induction”, IEEE Communications Magazine, (2015, Nov), 53(11), p42-48. [https://doi.org/10.1109/mcom.2015.7321970]
• Park, D, Kwak, K, Chung, W K, Kim, J, “Development of Underwater Short-Range Sensor Using Electromagnetic Wave Attenuation”, Oceanic Engineering, (2015, Nov), 41(2), p318-325. [https://doi.org/]
• Kwak, K, Park, D, Chung, W K, Kim, J, “Underwater 3D Spatial Attenuation Characteristics of Electromagnetic Waves with Omni-Directional Antenna” Trans, On Mechatronics IEEE/ASME, (2016, Jun), 21(3), p1409-1419. [https://doi.org/]
• Schloemann, J, Dhillon, H S, Buehrer, R M, “Toward a Tractable Analysis of Localization Fundamentals in Cellular Networks”, IEEE Transactions on Wireless Communications, (2016, Mar), 15(3), p1768-1782. [https://doi.org/10.1109/twc.2015.2496273]
• Lee, J C, Nam, S W, “Effective area of a receiving antenna in lossy medium”, Antennas and propagation IEEE Transactions, (2009, Jun), 57(6), p1843-1845. [https://doi.org/10.1109/tap.2009.2019988]
• Balanis, C A, “Antenna theory : Ch. 2 Basic parameter of antenna”, (2005), John Wiley, New York. [https://doi.org/]
• Buck, H, “Engineering Electromagnetics”, (2006), 7th, McGraw-hill, Boston. [https://doi.org/]
• Kwak, K, Park, D, Chung, W K, Kim, J, “Underwater E-plane Attenuation Model of Omnidirectional Antenna Using Half Power Beam Width (HPBW)”, Journal of Institute of Control, Robotics and Systems, (2015, Nov), 21(11), p1050-1056. [https://doi.org/10.5302/j.icros.2015.15.0146]
• Park, D, Kwak, K, Chung, W K, Kim, J, “Infrastructure based Localization System using Underwater Wireless Sensor Network”, Journal of Institute of Control Robotics and Systems, (2012, Aug), 18(8), p699-705. [https://doi.org/10.5302/j.icros.2012.18.8.699]