[ ARTICLE ]

Journal of Korea Robotics Society - Vol. 11, No. 2, pp.51-59

ISSN: 1975-6291 (Print) 2287-3961 (Online)

Print publication date May 2016

Received 25 Sep 2015 Revised 6 Jan 2016 Accepted 14 Jan 2016

DOI: https://doi.org/10.7746/jkros.2016.11.2.051

수중 영상 소나의 번들 조정과 3차원 복원을 위한 운동 추정의 모호성에 관한 연구

신영식¹ ; 이영준² ; 최현택² ; 김아영^†

Bundle Adjustment and 3D Reconstruction Method for Underwater Sonar Image

Young-Sik Shin¹ ; Yeong-jun Lee² ; Hyun-Taek Choi² ; Ayoung Kim^†

1Civil and Environmental Engineering, KAIST (youngsik.shin@kaist.ac.kr
2Korea Research Institute Ship and Ocean engineering (KRISO) [ leeyoungjun,htchoi]@kriso.re.kr

†Corresponding Author : Civil and Environmental Engineering, KAIST, 291 Daehak-ro, Daejeon, Korea ( ayoungk@kaist.ac.kr)

Abstract

In this paper we present (1) analysis of imaging sonar measurement for two-view relative pose estimation of an autonomous vehicle and (2) bundle adjustment and 3D reconstruction method using imaging sonar. Sonar has been a popular sensor for underwater application due to its robustness to water turbidity and visibility in water medium. While vision based motion estimation has been applied to many ground vehicles for motion estimation and 3D reconstruction, imaging sonar addresses challenges in relative sensor frame motion. We focus on the fact that the sonar measurement inherently poses ambiguity in its measurement. This paper illustrates the source of the ambiguity in sonar measurements and summarizes assumptions for sonar based robot navigation. For validation, we synthetically generated underwater seafloor with varying complexity to analyze the error in the motion estimation.

Keywords:

Imaging Sonar, Bundle adjustment, 3D reconstruction

1. 서 론

최근 로보틱스와 무인자동차 기술의 발달로 광학 카 메라와 레이저 스캐너 등의 다양한 센서를 이용한 외부 환경 인식에 관한 연구가 활발하게 이루어지고 있다. 특 히 광학 영상의 기하학적인 특정들이 잘 규명되면서 카 메라의 운동과 장면의 구조를 복원하는 연구가 활발히 진행되었다. 다시점 영상의 움직임 기반 구조복원(Structure from motion) 문제는 ^[3]에서 상세히 다루어졌으며, 번들 조정 알고리즘을 이용하여 카메라의 움직임과 3차원 장 면을 모두 복원하는 방법을 보였다. 번들 조정은 카메라 의 움직임과 여러 개의 대응점을 묶음으로 다루어 재사 영 오차를 최소화하도록 최적화하는 과정을 지칭하는 용어이다. 이러한 방식으로 다시점 영상 기반의 구조 복 원 문제를 다루는 경우 영상들 사이의 대응점을 이용하 여 다시점의 영상의 움직임을 알아내고, 그 대응점을 이 용하여 장면의 구조 복원을 수행하게 된다. 더 정확하고 강건한 번들 조정 방법을 위해서 ^[16]에서는 에러 모델 을 제시하고 그 민감도를 분석하였으며 Robustified Least Square와 같은 보다 강건한 번들조정 기법을 제안하였 다. 특히, SIFT (Scale Invariant Feature Transform)^[8]와 SURF (Speed Up Robust Feature)^[9] 등의 강건한 특징점 검출 기법들이 등장하여 보다 정확한 대응점을 추출할 수 있게 되면서 동일한 장소에서 찍힌 온라인상의 이미 지들로부터 유명 거리나 관광지 등의 장소를 3차원으로 복원하기에 이르렀다^[10]. 그러나 수중 환경에서 광학 카 메라 영상을 취득하는 것은 빛이 통과하는 매개체가 다 르기 때문에 가시 광선의 감쇠 및 산란 등의 영향을 받는 다. 또한 물의 탁도에 의해 가시거리가 제한되며, 심해의 경우에는 부족한 조명으로 인해 인공 광원에 의존한 영 상만이 획득 가능하다는 등의 어려움이 따른다. 영상 정 보의 한계로 인해 기존의 수중 로봇 항법 연구는 수중 음원^[17]을 사용하거나 Doppler Velocity Log (DVL)와 같 이 매우 정밀한 odometry를 이용^[18]하여 이루기도 하였다.

또한 수중 환경의 한계를 극복하기 위하여 수중 환경 에서는 고해상도 수중 영상 소나를 이용한 환경 인식에 관한 연구가 활발히 이루어지고 있다^[19]. 광학 영상에 비 해서는 저해상도의 품질의 영상을 제공하지만 영상 소 나의 성능에 따라 수백 미터 거리까지 관측이 가능하며 빛과 탁도의 영향을 받지 않기 때문에 수중 환경에서는 광학 카메라에 비해 활용도가 높다고 할 수 있다. Fig. 1은 고해상도 영상 소나의 대표적 모델인 미국 Sound metric의 Dual-frequency IDentification SONar (DIDSON) 와 그것을 이용하여 획득한 영상을 보여준다.

Fig. 1

DIDSON and sonar image

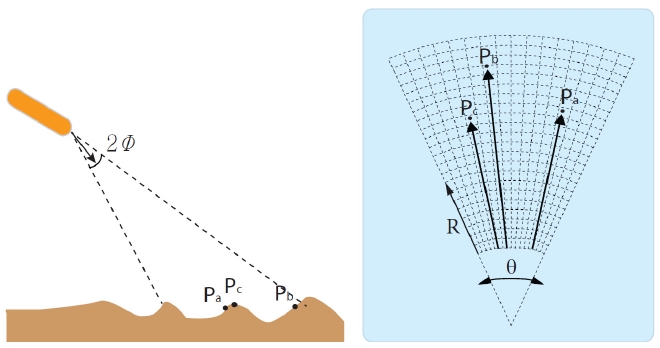
영상 소나는 광학 카메라와 달리 영상으로부터 해당 지점의 거리 ℜ과 방위각 θ의 직접 획득이 가능하다. 하 지만 상하각 φ의 정보가 소실되어 3차원의 실세계를 표 현하는데 한계를 가진다. 이러한 소나 영상의 기하학적 모호성을 분석하고 이를 극복하기 위한 연구들이 진행 되었다. ^[6]에서는 지배적인 평면 구조를 기반으로 두 시점의 소나 영상에서 움직임을 추정 할 때 다중 해가 존재한다는 사실을 이론적으로 분석하였다. ^[5]는 해저 면을 탐사하는 단일 소나 영상에서 지배적인 평면 구조 를 추정하는 방법을 제안하였고 관측된 물체의 그림자 를 이용하여 더 정확한 상하각을 추정하는 방법을 제안 하였다. 이러한 연구를 바탕으로 ^[14]는 관측된 물체의 그림자의 움직임을 고려한 모션추정 방법을 제안하여 그 정확도를 높였다.

고해상도 영상 소나를 이용한 초기 연구들은 광학 카메 라에서 사용하는 특징점 검출 기법을 도입하여 2D 환경 을 가정하여 모션 추정 및 영상 정합에 이용하였다^[11-13]. 그리고 최근에는 수중 환경에서 우수한 성능을 보이는 소나 영상을 이용하여 소나의 움직임을 추정하거나 수 중 로봇의 항법에 적용 하려는 연구가 많이 수행 되어 왔다. ^[7]은 연속적인 두 시점의 소나 영상이 비교적 평 평한 해저면을 바라보고 있다고 가정하고 각 영상 좌표 계 상에서 두 영상의 대응점들의 관계를 선형 변환관계 로 근사하여 특이값 분해(Singular value decomposition)를 이용하여 상대적인 3차원 움직임을 추정하고 그 성능과 정확도를 비교하였다. 3차원에서 영상 소나의 6D 움직 임이 추정이 가능하지만 소나 영상의 기하학적 한계로 인해 x, y축 방향의 회전 운동과 z방향의 선형 운동의 불확실성이 꽤 크다는 것을 실험을 통해 분석하였다. ^[2] 는 k-means 군집화 알고리즘을 이용하여 소나 영상에서 물체 영역을 검출하고, 검출 영역을 가우시안 맵 (Gaussian map) 기반의 특징으로 나타내고 이를 이용하여 영상 소 나의 움직임을 추정하는 연구를 수행하였다. ^[5]에서는 장면 표현 방법을 이용하여 상하각 맵(Elevation map)을 만들어 3차원 장면 인식에 이용하였다. ^[4]는 연속적으 로 얻은 해저면 소나 영상에서 NDT (Normal Distribution Transform)을 이용하여 환경 정보를 인식하고 수중 로봇 의 움직임을 2차원으로 한정하여 항법에 이용하였다. ^[15]에서는 광학 영상에서의 움직임 기반 구조 복원 방 법 중 하나인 번들 조정 방법을 소나 영상에 적용하여 평면에 대한 가정 없이 움직임 기반 구조 복원 문제를 해결하고자 하였다. 하지만 영상 소나의 기하적 모호성 으로 인해 몇 가지 degenerate case가 존재하며 해의 수렴 을 위해서는 최적화 알고리즘의 초기값이 매우 중요하 였다.

수중환경에서 영상 소나의 높은 활용도에도 불구하고 소나 영상이 갖는 기하학적 한계로 인해 움직임 기반 구조복원 문제를 해결하는데 제한이 따른다. 본 논문에 서는 수중 환경의 소나 영상을 이용한 번들 조정 방법과 구조 복원 방법에 대하여 2D 환경으로 제한한 방법에서 3차원 환경을 위한 방법으로 확장하여 각 기법에 관하여 비교 분석하고 영상 소나의 기하적 모호성으로 인한 제 한점에 대해 기술하고자 한다. 논문의 구성은 다음과 같 다. 본론에서 수중 소나 영상의 번들 조정 방법과 기하적 모호성에 대하여 설명하고 결론에서 모의 실험 결과를 통해 제안하는 연구내용을 분석한다.

2. 영상 소나의 움직임 기반 구조 복원

2.1. 수중 영상 소나의 좌표계

두 시점의 소나 영상의 움직임 기반 구조 복원에 앞서 소나 영상의 좌표계에 대한 이해가 필요하다. 본 연구에 서는 Fig. 2와 같이 영상 소나가 해저면을 바라보고 있는 상황을 가정하였다. [1, 4–6]에서 소개된 바와 같이 영상 소나의 3차원 좌표계 상의 한 점 P s는 직교좌표계와 구 좌표계에서 다음과 같은 관계로 나타난다.

Fig. 2

Sonar coordinate definition

P s = [Z s Y s Z s] = ℜ [cos ϕ sin θ cos ϕ cos θ sin ϕ] [θ ϕ ℜ] = [tan − 1 (X s Y s) tan − 1 (Z s X s 2 + Y s 2) X s 2 + Y s 2 + Z s 2]

(1)

여기서 Xs, Ys, Zs 는 직교좌표계에서 나타낸 영상 소 나의 한 점의 좌표이며 ℜ, θ, φ는 동일한 한 점을 구좌표 계에서 나타냈을 때 각각 거리, 방위각, 상하각을 나타낸다.

소나 영상은 위 좌표계의 XY평면상에서 나타나며 구 좌표계에서는 상하각이 0(φ = 0)인 지점에서 나타난다. 이러한 투영 관계의 결과로 영상 소나의 이미지 평면에 서 나타난 한 점은 아래와 같이 표현되어진다.

s = [x s y s] = ℜ [sin θ cos θ]

(2)

여기서 x_s, y_s는 소나의 이미지 평면 상에서의 포인트 s의 위치이며, 이는 구좌표계에서 상하각 φ의 정보는 소실되고 거리 ℜ과 방위각 θ 만으로 표현된다.

2.2. 수중 소나 영상의 번들 조정

이 절에서는 다중시점 소나 영상의 움직임 기반 구조 복원 문제를 해결하기 위한 최적화 기법 중 하나인 번들 조정 방법에 관하여 설명한다. 소나 영상의 기하적 모호 성을 피하기 위해 비교적 평평한 해저면을 바라보며 움 직이는 수중 로봇을 가정하였다. DIDSON과 같은 영상 소나의 경우 전방의 해저면을 바라보도록 하여 수중 로 봇에 장착되어있으며 로봇의 항법을 위한 의미 있는 정 보를 획득하기 위해서는 반사파가 발생할 수 있는 해저 면이나 선박의 표면과 같은 비교적 평평한 평면 환경의 가정이 필요하다. 소나 영상을 이용한 움직임 기반 구조 복원 문제를 해결하기 위하여 부분적인 움직임과 영상 좌표계에서 대응점들만을 고려하여 최적화하는 방법을 먼저 설명하고 3차원 환경으로 확장한 방법을 기술하였다.

본 논문에서는 다음의 3가지 번들 조정 방법을 비교 분석한다.

방법1: 2D 모션-2D 영상간의 대응점을 이용
방법2: 3D 모션-3D 평면상의 대응점을 이용
방법3: 3D 모션-3D 환경의 대응점을 이용

2.2.1. 2D 모션-2D 대응점에서의 번들 조정

수중 로봇이 비교적 평평한 해저면을 바라보며 일정 한 깊이 하에서 움직인다고 가정했을 때, 이동 로봇은 2D 공간에서 움직인다고 할 수 있고 그 움직임 하에서 이미 지의 대응점들도 동일한 무한 평면상에 존재한다고 근 사할 수 있다. 이를 바탕으로 아래와 같은 목적함수를 정의하여 부분적임 움직임을 추정할 수 있다.

min R^, t^, s^∑ i = 1 N c d (s i, s^i) 2 + d (s ′ i, s^′ i) 2 s . t . s^′ i = R^s^i + t^

(3)

여기서 si, s′ i 은 대응되는 이미지 포인트 쌍을 의미하 며 s^ 은 해당 이미지 포인트의 추정값, R^, t^ 는 두 시점 간의 상대적인 공간 관계의 추정값을 의미한다. 그리고 d(⋅) 는 재사영 오차를 계산하기 위한 유클리디안 거리 함수를 나타낸다.

2.2.2. 3D 모션-3D 평면상의 대응점에서 번들 조정

대부분의 수중 로봇들은 모션을 추정하기 위하여 추 가적인 센서들을 장착하고 있으며 음파를 이용한 모션 추정 센서가 장착되어 있는 경우 해저면의 깊이 정보로 부터 희소한 점들을 계산해 낼 수 있고 대략적인 평면을 유추할 수 있다. 또한 ^[5]에서 제시한 방법을 이용하면 해저면을 탐사하고 있는 수중 로봇의 소나 영상으로부 터 상하각 정보를 추정해 낼 수 있다. 이와 같이 해저면 을 근사한 평면을 유추할 수 있는 경우에 3D 모션과 평 면, 평면상의 대응점들을 이용하여 상하각을 추정하고, 나아가 이를 번들 조정에 적용할 수 있다.

평면의 방정식을 이용한 상하각의 추정

3차원 포인트 P s 가 법선 벡터 n=[nx, ny, nz]T 의 평면 상에 놓여있을 때, 그 평면상의 포인트는 Ps⋅n=1 인 평 면의 방정식을 만족해야 한다. 이러한 구속 조건을 구좌 표계에서 아래 식과 같이 나타난다^[5].

(n x sin θ + n y cos θ) cos ϕ +n z sin ϕ = 1 ℜ

(4)

여기서 거리 ℜ과 방위각 θ는 소나 영상으로부터 직접 획득이 가능하며 평면의 정규벡터를 알고 있으면 상하 각 φ를 직접 계산해 낼 수 있다.

3차원 평면을 이용한 소나 영상의 번들 조정

모션 R과 t의 상대적인 공간 관계에서 첫 번째 소나 영상의 점 s 는 두 번째 소나 영상 좌표계의 대응점 s′ 로 투영된다. 광학 카메라 영상과는 달리 상하각 φ가 소실 되어 영상 평면에 나타나게 되며 이러한 변환 관계는 다음과 같다.

(x s y s) n → (X s Y s Z s) R, t → ℜ ′ (cos ϕ ′ sin θ ′ cos ϕ ′ cos θ ′ sin ϕ ′) ϕ = 0 → ℜ ′ s (sin θ ′ s cos θ ′ s) = (x ′ s y ′ s)

(5)

여기서 영상의 점 s 는 추정 평면을 이용하여 3차원공 간의 점 P s 로 변환되며 이 점은 현재 추정한 상대적 위치 관계 R과 t를 이용하여 다음 위치의 영상 소나 의 좌표 계로 변환된다. 변환된 3차원 점은 상하각 φ = 0을 이용 하여 두 번째 소나 영상의 이미지 평면으로 사영된다. 이 러한 변환 관계를 이용하여 재사영 오차를 이용한 목적 함수를 다음과 같이 정의하여 번들 조정에 이용하였다.

min h^, x^∑ i = 1 N c d (s i, s^i) 2 + d (s ′ i, s^′ i) 2 s . t . s^′ i = h (h^, s^i)

(6)

where, h^=[R^, t^, n^]T

여기서 si, s′ i 은 대응되는 이미지 포인트 쌍을 의미하 며 s^ 은 해당 이미지 포인트의 추정값, R^, t^ 는 두 시점 간의 상대적인 공간 관계의 추정치를 의미하고 n^ 은 평면 의 법선 벡터의 추정값을 의미한다. d(⋅) 는 유클리디언 거리 함수를 나타내며 h(⋅) 는 두 소나 영상간의 변환 관계에 관한 함수이다.

2.2.3. 3D 모션-3D 대응점에서 번들 조정

고해상도 수중 소나 영상들은 비교적 작은 시야각(FOV, Field-Of-View)을 갖는다. 대표적인 고해상도 소나 DIDSON 의 경우 상하각이 ±7°이내(cos 7°=0.9925)로 거리 ℜ과 방위각 θ를 알고 있는 것만으로도 3차원 좌표가 어느 정도 추측이 가능하다. 이를 번들 조정의 초기값으로 이 용하여 다음과 같은 목적 함수를 정의하여 움직임 기반 구조 복원 문제에 적용 할 수 있다.

min h^, x^∑ i = 1 N c d (s i, s^i) 2 + d (s ′ i, s^′ i) 2 s . t . s^′ i = h (h^, X^i) | cos ϕ =0, s i^= X^i | cos ϕ =0

(7)

where, h^=[R^, t^]T

여기서 si, s′ i 은 대응되는 이미지 포인트 쌍을 의미하 며 s^ 은 해당 이미지 포인트의 추정 값, R^, t^ 는 두 시점 간의 상대적인 공간 관계의 추정치를 의미하고 X^은 복 원하는 3차원 점의 추정 값을 의미한다.

3. 소나 영상의 기하적 모호성

3.1. 임의의 모션에서 상하각의 모호성

이 절에서는 두 시점에서 소나 영상의 움직임을 알 고 있는 상황에서 대응점의 기하적 모호성에 관하여 설 명한다. 두 시점의 영상 소나가 회전운동 R, 직선운동 t의 관계로 표현될 때 3차원 상의 두 대응점은 다음과 같이 나타난다.

P s = R P ′ s + t

(8)

소나 영상에서 구좌표계로 나타낸 대응점의 거리 ℜ 과 방위각 θ 를 직접 얻을 수 있기 때문에 상하각 φ 를 계산할 수 있으면 영상 소나의 좌표계에서 3차원 점들을 바로 복원할 수 있다. 이를 계산하기 위해서 두 대응점 간의 관계를 나타낸 위의 식을 벡터의 크기를 이용하여 전개하면 다음과 같다.

‖ P s ‖ 2 = ‖ R P ′ s + t ‖ 2 = ‖ P ′ s ‖ 2 + 2 (t T R) P ′ s + ‖ t ‖ 2

(9)

두 시점에서의 움직임 R, t와 영상에서의 대응점들 s=(xs, ys), s′=(x′ s, y′ s) 을 알고 있으므로 3차원 포인 트 P s 는 다음과 같이 나타난다.

P s = [x s cos ϕ y s cos ϕ x s 2 + y x 2 sin ϕ]

(10)

최종적으로 회전행렬 R 의 각 열 벡터를 ri로 정리하여 위의 3차원 포인트 P s 를 식 (9)에 대입하여 정리하면 아 래와 같은 방정식을 얻을 수 있다.

where,

A cos ϕ = B sin ϕ = C A= (t T r 1) x ′ s + (t T r 2) y ′ s B = (t T r 3) (x ′ s 2 + y s 2) C = 12 (‖ P s ‖ 2 − ‖ P ′ s ‖ 2 − ‖ t ‖ 2)

(11)

위의 방정식은 삼각함수의 합성을 이용하여 해를 계 산할 수 있지만 삼각함수의 주기 내에서 항상 두 개의 해가 존재하게 된다. 결과적으로 소나 영상의 기하적 모 호성으로 인해 두 시점에서 움직임을 정확히 알고 있다 고 하더라도 상하각 φ를 유일해로 얻을 수 없게 된다.

3.2. 응용 방안

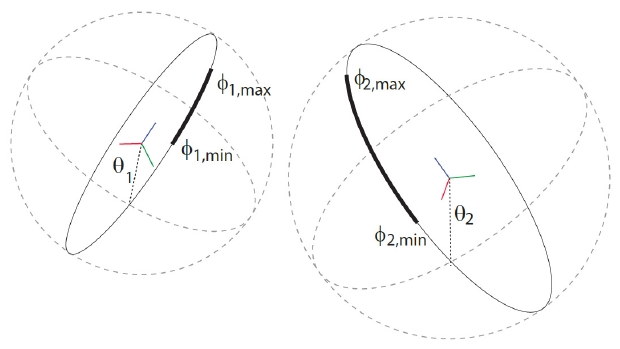
소나 영상은 거리 ℜ과 방위각 θ를 직접 얻을 수 있지 만 상하각 φ는 소실된다. 이러한 이유로 두 시점간의 움직임을 알고 있다고 하더라도 두 개의 상하각이 존재 하는 모호성을 띄고 있다. 또한 상하각이 소실되어 나타 나기 때문에 Fig. 3처럼 두 시점의 영상에서 대응점들을 3차원으로 나타냈을 때 고리의 형태를 띄게 되며 그 고 리들이 교차하기만 하면 항상 해가 존재하게 된다. 이러 한 이유로 두 시점의 소나 영상의 움직임 기반 구조복원 문제는 소나 영상의 제한적인 시야각으로 상하각의 범 위가 한정되어 Fig. 3에서처럼 상하각의 최대, 최소값을 알고 있다고 하더라도 두 굵은 실선으로 나타난 호의 교차점을 찾는 문제이기 때문에 무수히 많은 해가 존재 하게 된다. 상하각의 이러한 기하적 모호성으로 인해 [2, 4–7]에서 다음과 같은 방법들이 소개되었다.

Fig. 3

Visual ambiguity of sonar model

2D 움직임과 환경을 가정하여 부분적인 움직임 만 을 추정
해저면을 평면으로 가정하여 상하각의 맵을 추정하 고 물체영역과 그 그림자를 이용하여 상하각 맵을 보정하여 정확도를 높임
상호 보완적인 센서정보를 사용하여 실제 값에 가 까운 초기치를 사용하여 번들 조정에 이용
광학 카메라와 영상 소나를 융합하여 두 센서 간의 서로 다른 기하적 모호성 극복

4. 실험 결과

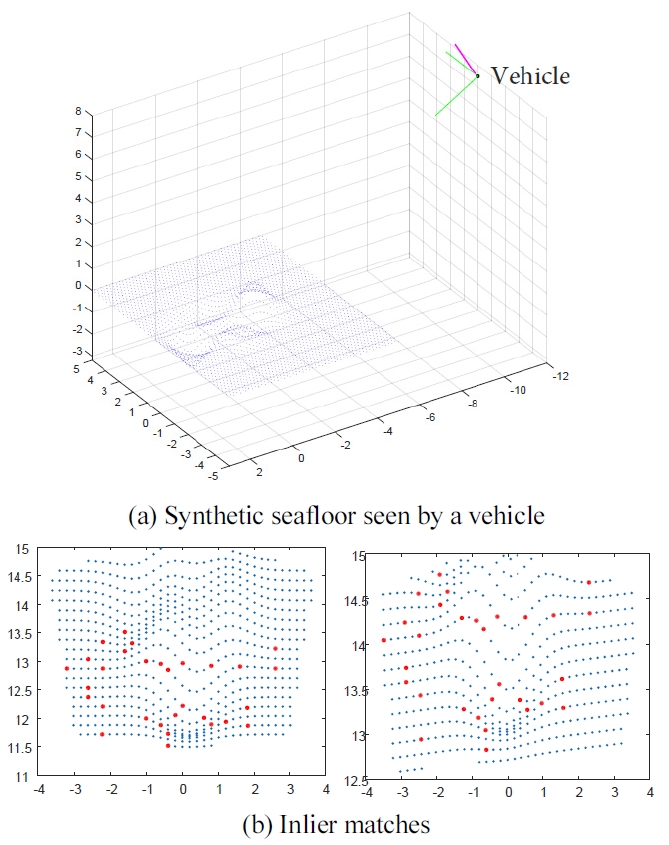
앞에서 제시한 번들 조정의 성능을 검증하기 위하여 MATLAB을 이용한 모의 실험을 진행하였다. Fig. 4의 (a)와 같은 3차원 환경에서 발생시킨 점들을 서로 다른 두 시점의 소나 영상에 투영시킨 후 일정 개수의 대응점 을 발생시켜 번들 조정에 이용하였다.

Fig. 4

Depiction of synthetic data generation

4.1. 번들 조정 방법에 따른 모션 추정 결과

이 절에서는 본론에서 제시한 3가지 방법의 모션 추정 결과를 비교하기 위하여 평평한 평면 환경을 가정하여 모의 실험을 진행하였다. 소나의 기준 위치에서 직선운 동 ±3.25 m, 회전운동 ±15° 이내의 임의모션을 발생시 켰으며 직선운동 ±0.3 m, 회전운동 ±3° 이내의 가우시 안 노이즈를 발생시켜 각각의 방법에 대해서 번들 조정 을 수행하였다.

2D 모션-2D 대응점(방법1)에서의 번들 조정은 t_x, t_y, θ_z 의 부분적 움직임만을 추정하였으며 실제 움직임에 일정 노이즈를 추가하여 번들 조정을 위한 초기값으로 이용하였다. 위의 과정을 각 방법에 따라 500회씩 수행 하였으며 번들 조정이 수렴한 경우의 결과만을 비교하 기 위해 상하위 5%의 결과를 제외하여 오차의 평균과 표준편차를 Table 1에 나타내었다.

Table 1

Experimental Results by Bundle Adjustment Methods

평평한 평면환경을 가정한 실험이었기 때문에 3가지 방법 모두 비교적 우수한 결과를 보였으며, 평면이라는 구속조건이 포함되어있는 3D-3D 평면(방법2) 환경 모델 에서의 번들 조정이 가장 우수한 결과를 보였다. 단, 소 나 영상의 기하적 모호성으로 인해 본 모의 실험에서는 소나의 초기 모션 정보를 어느 정도 알고 있음을 가정하 였으며 움직임에 관한 초기값이 실제 값과 많이 다른 경우는 번들 조정이 수렴하지 못하는 경우가 빈번히 발 생하였다. 특히 3D 모션-3D 대응점(방법3)에서의 경우 모션의 초기값의 불확실성이 커지는 경우 번들 조정이 수렴 조건을 만족하지 못하는 경우가 빈번하였다.

4.2. 평면의 복잡도에 따른 모션 추정 결과

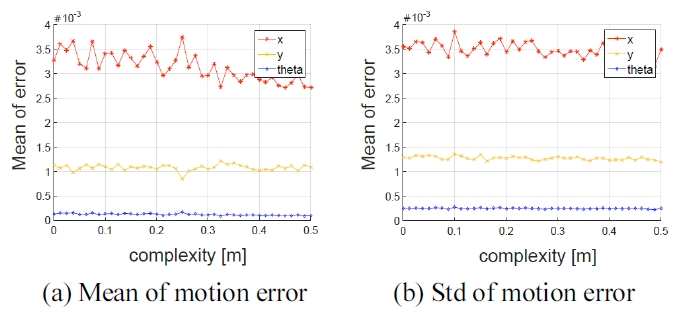
실제 해저 환경의 경우 완벽한 평면의 해저면이 거의 존재하지 않으며 다양한 개체들로 인해 복잡한 구조의 환경을 구성하게 된다. 이 절에서는 이러한 환경에서의 모션 추정의 정확도와 불확실성을 분석하기 위하여 평 면의 복잡도를 증가시키면서 번들 조정을 수행하고 그 결과를 분석하였다. 평면의 복잡도는 Fig. 4의 모의 실험 환경에서 3차원 구조의 최고점을 의미한다. 이전 절의 실험과 동일하게 임의 모션과 노이즈를 발생시켜 본론 에서 제시한 3가지 방법에 대해서 평면의 복잡도마다 200회씩 실험을 수행하였다.

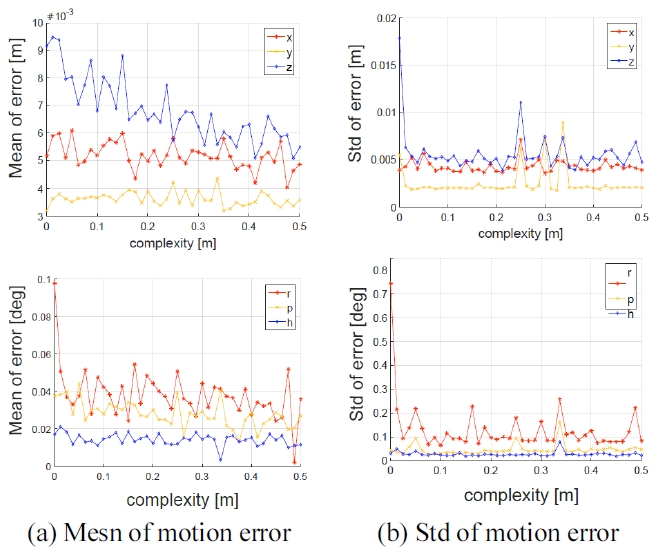
Fig. 5는 2D 모션-2D 대응점 (방법1)에서의 번들 조정 결과이다. 부분적인 움직임만을 추정하였기 때문에 평 면의 복잡도가 증가하더라도 모션 추정 오차의 평균은 거의 일정 했으며 추정 오차의 표준 편차 또한 일정한 경향을 보임을 알 수 있다.

Fig. 5

Performance evaluation of 2D-2D points bundle adjustment by environment complexity

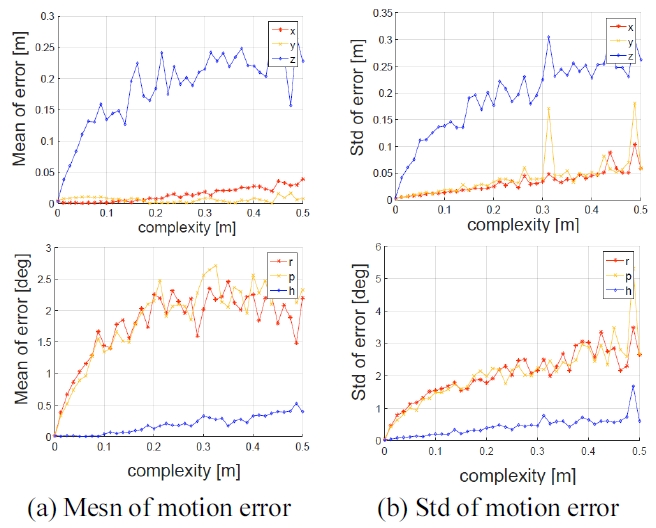
Fig. 6은 3D 모션-3D 평면상의 대응점에서의 번들 조 정 결과이다. 번들 조정이 수렴한 경우의 결과만을 비교 하기 위해 상하위 5%의 결과를 제외하여 200회 반복 수행한 오차의 평균과 표준편차를 그래프로 나타내었다. 평면의 복잡도가 증가함에 따라 모션 추정 오차의 평균 과 표준편차가 증가하는 경향을 보인다. 특히, 직선 운동 의 경우 z 축의 오차가 크게 증가하는 경향을 보이는데 반해 회전 운동의 경우는 x, y 축 방향에서 오차가 크게 증가하는 것을 확인할 수 있다. 이는 소나 영상에서 거리 ℜ과 방위각 θ는 직접 획득이 가능하지만 상하각 φ가 소실되어서 발생하는 기하적 모호성에서 기인한다.

Fig. 6

Performance evaluation of 3D-3D plane bundle adjustment by environment complexity

Fig. 7은 3D 모션-3D 대응점에서의 번들 조정 결과이 다. 번들 조정이 수렴한 경우의 결과만을 비교하기 위해 상하위 15%의 결과를 제외하여 200회 반복 수행한 오차 의 평균과 표준편차를 그래프로 나타내었다. 평면의 복 잡도가 낮을 때 모션 추정 오차가 앞의 두 결과에 비해 높게 나타나지만 평면의 복잡도에 관계없이 일정한 경 향을 보이는 것을 확인할 수 있다. 단, 위의 결과는 200회 의 반복실험 결과 중 상위와 하위의 데이터 중 15%를 제외하고 얻은 결과이다. 제외된 15%의 경우 모션의 초 기값의 실제 값과 차이가 커서 번들 조정이 수렴하지 못한 경우를 다수 포함 하고 있다는 것을 의미한다. 본 방법을 실제로 적용하기 위해서는 수중 로봇에 장착되 어있는 다른 센서들의 정보를 이용하여 비교적 정확한 모션 값을 번들 조정의 초기치로 이용하여야 한다.

Fig. 7

Performance evaluation of 3D-3D points bundle adjustment by environment complexity

5. 결 론

본 논문에서는 수중 소나 영상에서 움직임 기반 구조 복원 문제를 해결하기 위한 번들 조정 방법을 제시하고 기하적 모호성으로 인한 제한점을 분석하였다. 영상 소 나의 모션과 환경복원을 위하여 부분적인 움직임만을 추정하기 위한 방법에서 일반적인 3차원 환경을 위한 방법으로 확장하여 총 3가지 번들 조정 방법을 제시하였 다. 그리고 상하각 정보가 소실되어 나타나는 영상 소나 의 기하적 모호성에 대해 분석하였으며, 정확한 모션을 알고 있는 상황에서도 두 개의 해가 존재 함을 보였다. 이러한 영상 소나의 기하적 모호성으로 인해 움직임 기 반 구조 복원 문제를 해결 하는 것에 제약을 가지고 있음 을 보였으며 이러한 제한 사항을 고려한 응용방안에 대 해서 제안하였다. 또한 영상 소나를 이용한 움직임 기반 구조 복원 문제를 더 효과적으로 해결하기 위해 제안하 는 3가지 방법 중 한가지만을 사용하기보다는 각 모델의 특성에 따라 모델 선택(model selection)기법을 도입하여 상황에 따라 가장 적절한 모델을 이용하여 수중로봇에 항법에 적용하는 연구가 필요할 것으로 보인다.

Acknowledgments

This research was a part of the project titled ‘Development of an autonomous ship-hull inspection system’, funded by the Ministry of Oceans and Fisheries, Korea. This research was also funded by KRISO (#N04150009) and u-city program by Ministry of Land, Infrastructure, and Transport, Korea.

References

Aykin, MD, Negahdaripour, S, “On feature extraction and region matching for forward scan sonar imaging”, In Proc. IEEE/MTS OCEANS Conf. Exhib, (2012), Oct, p1-9. [https://doi.org/10.1109/oceans.2012.6404983]
Murat, D Aykin, Shahriar, Negahdaripour, “On feature matching and image registration for two-dimensional forward-scan sonar imaging”, Journal of Field Robotics, (2013), 30(4), p602-623. [https://doi.org/10.1002/rob.21461]
Hartley, RI, Zisserman, A, “Multiple View Geometry in Computer Vision”, (2004), Cambridge University Press, ISBN: 0521540518, second edition. [https://doi.org/10.1017/CBO9780511811685]
Johannsson, H, Kaess, M, Englot, B, Hover, F, Leonard, JJ, “Imaging sonar-aided navigation for autonomous underwater harbor surveillance”, In proc. IEEE/RSJ Intl. Conf. Intell. Robots Systems, (2010), Taipei, Taiwan, Oct. [https://doi.org/10.1109/iros.2010.5650831]
Negahdaripour, S, “On 3-d scene interpretation from f-s sonar imagery”, In Proc. IEEE/MTS OCEANS Conf. Exhib, (2012), Oct, p1-9. [https://doi.org/10.1109/oceans.2012.6404921]
Negahdaripour, S, “Visual motion ambiguities of a plane in 2-d fs sonar motion sequences”, Comput. Vis. Image Underst, (2012, June), 116(6), p754-764. [https://doi.org/10.1016/j.cviu.2012.02.005]
Negahdaripour, S, Assalih, H, Petillot, Y, Brisson, LN, “Performance and accuracy in visual motion computation from fs sonar video sequences”, In Proc. IEEE/MTS OCEANS Conf. Exhib, (2010), Sept, p1-7. [https://doi.org/10.1109/oceans.2010.5664504]
Lowe, DG, “Distinctive image features from scale invariant keypoints”, Intl. J. Computer Vision, (2004), 60(2), p91-110. [https://doi.org/10.1023/b:visi.0000029664.99615.94]
Bay, H, Ess, A, Tuytelaars, T, Van Gool, L, “Speeded up robust features (SURF)”, Computer Vision and Image Understanding, (2008), 110(3), p346-359. [https://doi.org/10.1016/j.cviu.2007.09.014]
Nat`alia, Hurt os, David, Ribas, Xavier, Cufi, Yvan, Petillot, Joaquim, Salvi, “Fourier-based registration for robust forward-looking sonar mosaicking in low-visibility underwater environments”, Journal of Field Robotics, (2015), 32(1), p123-151. [https://doi.org/10.1002/rob.21516]
Noah, Snavely, Steven, M Seitz, Richard, Szelisk, “Photo tourism: Exploring photo collections in 3d”, In SIGRAPH Conference Proceedings, (2006), New York, NY, USA, ACM Press, p835-846.
Negahdaripour, S, Firoozfam, P, Sabzmeydani, P, “On processing and registration of forward-scan acoustic video imagery”, In Computer and Robot Vision 2005. Proceedings, (2005), The 2nd Canadian Conference, May, p452-459. [https://doi.org/10.1109/crv.2005.57]
Trucco, E, Petillot, YR, Tena Ruiz, I, Plakas, K, Lane, DM, “Feature tracking in video and sonar subsea sequences with applications”, Computer Vision and Image Understanding, (2000), 79(1), p92-122. [https://doi.org/10.1006/cviu.2000.0846]
Negahdaripour, S, “On 3-d motion estimation from feature tracks in 2-d fs sonar video”, IEEE Transaction on Robotics Aug, (2013), 29(4), p1016-1030. [https://doi.org/10.1109/tro.2013.2260952]
Huang, T A, Kaess, M, “Towards acoustic structure from motion for imaging sonar”, In IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems, IROS, (2015). [https://doi.org/10.1109/iros.2015.7353457]
Triggs, Bill , , “Bundle adjustment—a modern synthesis”, Vision algorithms: theory and practice, (2000), Springer, Berlin, Heidelberg, p298-372.
Choi, J, Choi, H-T, “Underwater acoustic source localization based on the probabilistic estimation of direction angle”, Journal of Korea Robotics Society, (2014, Nov), 9(4), p206-215. [https://doi.org/10.7746/jkros.2014.9.4.206]
Jeong, S, Ko, N-Y, Choi, H-T, “Comparison of attitude estimation methods for DVL navigation of a UUV”, Journal of Korea Robotics Society, (2014, Nov), 9(4), p16-224. [https://doi.org/10.7746/jkros.2014.9.4.216]
Lee, Y, Choi, J, Choi, H-T, “Underwater robot localization by Probability based object recognition framework using sonar image”, Journal of Korea Robotics Society, (2014, Nov), 9(4), p232-241. [https://doi.org/10.7746/jkros.2014.9.4.232]

신 영 식

2013 인하대학교 전기공학과(공학사)

2015 KAIST 로봇공학학제전공(공학석사)

2015 ~ 현재 KAIST 건설 및 환경공학과 박사 과정

관심분야: SLAM, 로봇비전, 수중 로봇

이 영 준

2009 충남대학교 메카트로닉스공학과(학사)

2014 충남대학교 메카트로닉스공학과(석사)

2011 ~ 현재 한국해양과학기술원 부설 선박 해양플랜트연구소 해양시스템연구부 연구원

관심분야: 수중 로봇, 영상처리, 영상소나

최 현 택

1991 한양대학교 전자공학(학사)

1993 한양대학교 전자공학(석사)

2000 한양대학교 전기공학(박사)

1993 ~ 1995 KT 연구개발원 소프트웨어 연구소 전임연구원

1996 ~ 2000 한양대학교 컴퓨터 교육위원회 강사

2000 ~ 2003 하와이 주립대학교 Autonomous System Lab. 박사 후 연구원

2003 ~ 현재 한국해양과학기술원 부설 선박해양플랜트연구소 해양 시스템연구부 책임연구원

관심분야: 수중 로봇, 해양 시스템, 강인제어

김 아 영

2005 서울대학교 기계항공공학과(공학사)

2007 서울대학교 기계항공공학과(공학석사)

2012 미시간대학교 기계공학과(공학박사)

2014 ~ 현재 KAIST 건설 및 환경공학과 조교수

관심분야: SLAM, 로봇 비전, 항법, 영상 처리

		t_x(m)	t_y(m)	t_z(m)	θ_x(deg)	θ_y(deg)	θ_z(deg)
2D-2D points	Avg	0.0033	-0.0011	-	-	-	0.0057
2D-2D points	Std	0.0036	0.0013	-	-	-	0.0172
3D-3D plane	Avg	0.0035	0.0042	0.0028	0.0166	0.0085	0.0131
3D-3D plane	Std	0.0031	0.0019	0.0037	0.0482	0.0414	0.0134
3D-3D points	Avg	0.0052	0.0032	0.0092	-0.0978	0.0377	0.0172
3D-3D points	Std	0.0039	0.0055	0.0179	0.7423	0.0436	0.0301