사각형 특징 기반 Visual SLAM을 위한 자세 추정 방법
© Korea Robotics Society. All rights reserved
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this paper, we propose a method for estimating the pose of the camera using a rectangle feature utilized for the visual SLAM. A warped rectangle feature as a quadrilateral in the image by the perspective transformation is reconstructed by the Coupled Line Camera algorithm. In order to fully reconstruct a rectangle in the real world coordinate, the distance between the features and the camera is needed. The distance in the real world coordinate can be measured by using a stereo camera. Using properties of the line camera, the physical size of the rectangle feature can be induced from the distance. The correspondence between the quadrilateral in the image and the rectangle in the real world coordinate can restore the relative pose between the camera and the feature through obtaining the homography. In order to evaluate the performance, we analyzed the result of proposed method with its reference pose in Gazebo robot simulator.
Keywords:
Visual SLAM, Geometric Visual Feature, Robot Vision, Pose Estimation1. 서 론
카메라는 저비용으로 다양한 정보를 수집할 수 있는 센서로서 로봇의 임무수행을 위한 환경 인지기술에 적 용되어 센서의 특성을 효과적으로 이용하기 위한 많은 연구가 이루어져 왔다[1,2]. 특히 Visual SLAM으로 알려 진 카메라를 이용한 위치인식과 지도작성은 GPS를 사용 할 수 없는 실내 혹은 실외의 음영지역에서 효율적으로 로봇의 위치를 추정할 수 있는 방법으로 제안되어 왔다. 그러나 여타 SLAM연구와 마찬가지로 동적으로 변화하 는 환경에서의 작동, drift에 의해 발생하는 에러를 효과 적으로 제거하는 것에 어려움을 겪고 있다.
Visual SLAM의 랜드마크로는 여러 연구에서 점 또는 국소 패치만을 사용하여 SLAM을 수행해 왔다. 저 수준 의 특징은 추출과 정합이 간편하고 일반적인 환경에 대 해 널리 사용할 수 있다는 장점이 있으나 추출 방법이 단순하여 한 영상에서 추출되는 특징의 개수가 매우 많 아 정보를 모두 이용하기에는 복잡하고 연산 부담이 늘 어나므로 제한된 수의 랜드마크를 사용한다[3]. 또한 다 양한 부가 정보를 특징으로 활용할 수 있는 인공적인 구조물이 있는 실내환경, 도심지와 같은 곳에서도 저 수 준의 특징을 이용하는 것이 최적의 방법이라 할 수 없을 것이다.
이 논문에서는 Visual SLAM을 위해 영상에서 사각형 을 추출하여 카메라와 특징 간의 자세를 간단하고 정확 하게 추정하는 방법을 소개한다. 이 방법은 저 수준의 특징인 코너, 국소 패치만을 이용한 카메라의 자세 추정 방법과 다르게 한 개의 특징 추출만으로 대응하는 카메 라의 자세를 복원할 수 있다.
2. 관련 연구
일반적인 SLAM의 연구에서는 초음파, 레이저 거리 센서 등 다양한 종류의 센서가 사용되어 오고 있다. 이들 중에서 카메라는 많은 정보를 제공하는 대신 처리하는 방법에 따라 많은 차이를 보여 따로 Visual SLAM으로 지칭한다. Visual SLAM은 필터링 방법을 이용한 접근 과 최적화를 이용한 접근이 있다. 전자는 주로 로봇 분야 에서 연구되어 온 방법이고 후자는 컴퓨터 비전의 bundle adjustment를 이용한 structure from motion연구에서 파 생된 것으로 두 방법에 대한 이론적, 실험적 분석이 [4] 에 발표되어 있다. 또 사용하는 카메라의 구성에 따라 단안카메라를 사용한 방법[5,6,7], 양안 카메라를 사용한 방법[8], 전방위 카메라를 사용한 방법[9], RGB-D카메라 를 사용한 방법[10] 등이 있다. 위의 연구에서는 영상에서 점 또는 15×15픽셀 정도의 국소 패치 특징을 찾아 연속 된 영상에서 특징간의 상관관계를 찾아 카메라의 자세 추정을 수행한다. 점 기반의 카메라의 실시간 동작 추정 방법으로는 추출된 특징의 재 투사 오차를 최소화하는 방법, 잡음에 강인한 RANSAC을 이용하는 방법이[11] 많 이 이용되어 왔다. 이와 같은 접근에서는 많은 수의 특징 점이 이용되는 복잡한 카메라 자세 추정 알고리즘이 전 체적인 처리 속도와 정확도에 가장 큰 영향을 주게 된다. 최근의 연구에서는 별도의 특징을 이용하지 않고 영상 의 photometric error를 최소화하여 motion을 추정하는 방법이[12,13] 소개되어 관련된 연구가 진행되고 있다. 특 징을 이용한 자세추정의 경우에서는[14] 점, 선분, 평면 등의 다양한 기하학적 특징을 융합하여 지도 작성 정확 도를 향상한 연구도 있다. 그러나 여전히 점 기반의 특징 을 이용한 접근을 바탕으로 하고 다른 기하적 특징은 정확도 향상을 위해 부분적으로만 응용되어 이 논문에 서 제안하는 방법과는 거리가 있다.
3. 선분카메라쌍을 이용한 카메라 자세 추정
3.1. 사각형 특징 기반의 카메라의 자세 추정
본 연구에서는 카메라의 자세를 추정하기 위해 영상 에서 추출 가능한 기하학적 특징인 사각형 특징을 이용 하는 방법을 제안한다. 위에서 소개한 복수의 점 특징의 대응 관계를 이용하여 다수의 영상에서의 재 투사 오차 를 최소화하는 카메라의 자세를 찾아내는 방법과는 다 르게 제안하는 방법에서는 단수의 영상에서 추출한 3차 원 평면 위 직사각형 특징을 통해 대응하는 카메라의 자세를 찾아낼 수 있다.
실제 3차원 공간의 직사각형에 대응되는 영상 내부의 사변형을 추출하였다고 가정할 때 이를 이용한 카메라 의 자세 추정은 몇 단계를 거쳐 수행된다. 먼저 추출된 사변형의 기하적 성질을 이용하여 원본 직사각형의 형 태로 복원할 수 있는 선분카메라쌍 알고리즘을 이용하 여 사각형을 복원한다[15]. 이 때 선분카메라쌍은 원본 사 각형의 형태만을 복원할 뿐, 정확한 크기를 알 수 없음에 주목한다. 이를 위해 스테레오 카메라를 이용하여 사각 형의 실제 크기를 찾는다. 찾아진 사각형의 꼭지점과 입 력된 영상 내부 사변형의 꼭지점 사이의 대응관계를 통 해 perspective 변환 관계를 유도한다. 이는 2D 호모그래 피에 해당하며 행벡터로 분리 후 간단한 계산을 거쳐 카메라의 자세를 유도할 수 있다[16].
3.2. 직사각형 복원을 위한 선분카메라쌍 방법
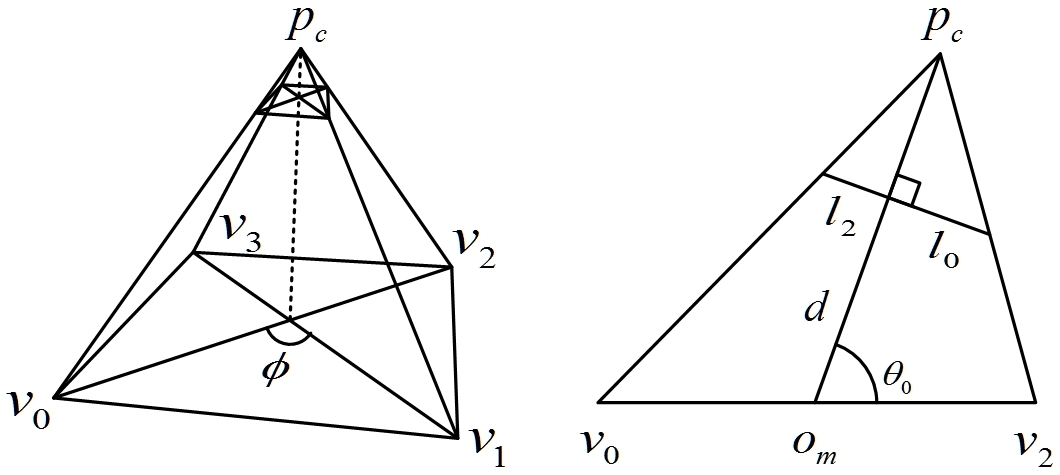
직사각형의 복원은 카메라의 투사구조 복원과 관련이 있다. 일반적으로 투사구조의 복원을 위해 카메라를 핀 홀 카메라 모델로 가정하고 다수의 점 대응쌍을 추출하여 수치해석적인 방법을 통해 유도한다. 그러나 같은 평면 위에 4점이 존재하는 직사각형 특징의 경우 특수한 기하 관계에 의해 카메라의 투사구조를 closed-form으로 계산 할 수 있다. 선분카메라쌍 알고리즘은 영상에서 perspective 변환에 의해 변형된 직사각형이 가질 수 있는 기하적 조건을 만족하는 사변형을 추출하여 원래의 직사각형의 형태를 복원하는 알고리즘이다. 직사각형은 중점에서 각 꼭지점에 이르는 거리와 종횡비로 유일하게 결정할 수 있다. 선분카메라쌍 알고리즘에서는 중심과 꼭지점 간의 거리를 1로 가정하여 이를 기준으로 카메라와의 상대 자세와 직사각형의 종횡비를 얻는다. Fig. 1의 좌측 에는 카메라 평면에 투영된 사변형과 직사각형 특징과 의 관계가 표현되어 있고 우측에는 단일 선분카메라의 형태가 설명되어있다. Table 1에는 선분카메라쌍을 이 용한 직사각형 복원 알고리즘이 서술되어 있다. 이 때 vi,i =1,2,3,4는 3차원 공간에서 사각형을 구성하는 각 꼭지점의 좌표들이다.
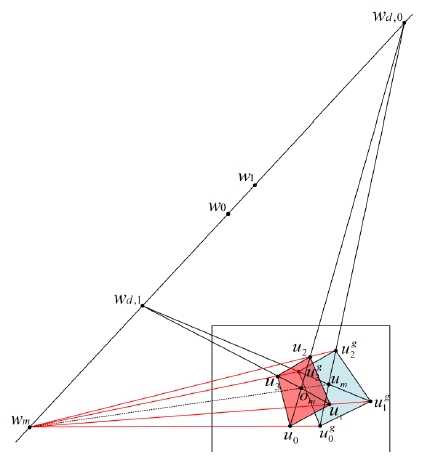
선분쌍 카메라는 사변형의 중심이 영상의 중심과 일 치하는 경우에만 적용할 수 있는 방법임에 유의한다. 이 는 소실점을 이용하여 사변형과 영상의 중심이 일치 하 고 inverse perspective warp시 합동 조건을 만족하는 임 시 사변형을 추출하여 간접적으로 직사각형을 복원할 수 있다[17]. 여기서 ui,i=1,2,3,4,
3.3. 스테레오 카메라를 통한 feature scale 결정
일반적으로 단안카메라를 이용한 카메라의 자세 추정 방법에서는 스케일에 대한 정보를 얻는 것은 불가능하 다. Table 1의 선분카메라쌍 방법을 이용한 직사각형 복 원 방법에서도 직사각형의 실제 크기를 알 수 없으므로 직사각형의 중점과 꼭지점까지의 길이를 1로 두고 형태 를 복원하였다.
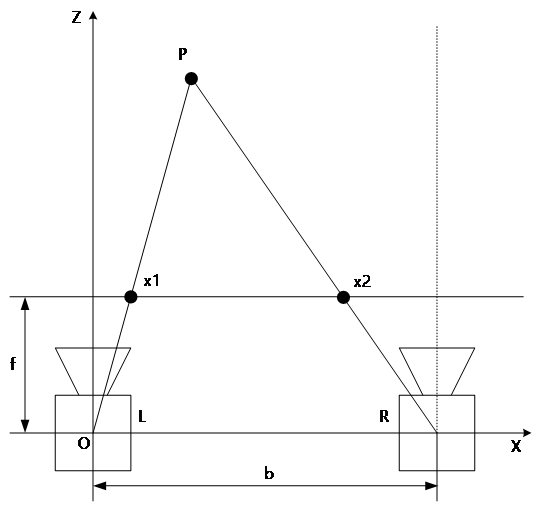
3차원의 카메라 자세를 완전하게 추출하기 위해서 여 기서는 베이스라인의 길이가 알려진 스테레오 카메라의 삼각측량법으로 특징의 크기를 추정하는 방법을 사용한 다. 베이스라인 b의 길이와 초점거리 f가 알려진 스테레 오 카메라쌍에서 두 개의 카메라에서 실제 공간 상의 점 P = [X Y Z]T에 대한 대응점을 x1, x2라고 할 때 관계 식을 식 (1)과 같이 표현할 수 있다.
| (1) |
Fig. 1의 선분카메라를 이용하여 직사각형의 중점과 카메라 중심 사이의 거리인 ∥ompc∥를 d[m]라 하고 직 사각형의 중점과 한 꼭지점 사이의 거리인 ∥omv0∥를 m[m]이라 할 때 두 값은 아래의 관계식을 이용하여 얻 어낼 수 있다.
| (2) |
| (3) |
3.4. 2D 호모그래피를 이용한 3차원 자세 추정
위에서 구한 직사각형 특징과 대응하는 입력 영상 내 부의 사변형을 이용하여 카메라의 자세를 추정하고자 한다. 주목할 것은 영상 내부의 사변형과 실제 직사각형 모두 평면 위에 존재하는 점으로 구성된 도형이라는 점 이다. 이에 4개의 대응되는 점들의 쌍으로 두 평면 사이 의 관계를 표현하는 호모그래피를 추출하여 카메라의 자세를 추출하고자 한다.
내부 파라미터 정보를 이용하여 정규화 된 영상 좌표 계 위의 점을 x라 하고 기준 좌표계 위의 점을 X라 할 때 두 점 사이의 대응 관계는 아래와 같이 표현할 수 있다.
| (4) |
P는 3×4의 행렬로서 4개의 열벡터로 구성되어 있다. 이 때 영상의 사변형에 대응하는 실제 직사각형은 기준 좌표계의 x-y평면에 존재한다고 가정하면 아래와 같이 정리할 수 있다.
| (5) |
이와 같이 3차원 기준 좌표계 상의 점의 차수가 줄어 들며 두 대응점의 관계가 2차원 평면 위의 점들의 관계 를 표현하는 호모그래피의 꼴로 표현되는 것을 알 수 있다.
두 평면의 회전을 표현한 회전행렬을 R, 천이 벡터를 t라고 할 때 각 열벡터는 두 평면 간의 회전과 천이에 대한 성분으로 표현된다. 호모그래피 변환 행렬의 첫 번 째와 두 번째 열벡터는 각각 회전행렬의 첫 번째와 두 번째 열벡터에 대응하고 세 번째 열벡터는 천이 벡터 t에 대응한다. 회전행렬은 정규직교 행렬이어야 하므로 이를 이용하여 회전행렬의 세 번째 열벡터는 아래의 식 으로 간단히 구할 수 있다.
| (6) |
이와 같이 카메라 좌표계에 대응하는 영상 좌표계와 특징을 중심으로 한 기준 좌표계 사이의 상대적인 자세 관계를 유도할 수 있다. 주의할 것은 호모그래피에서 회 전행렬을 추출할 때, 회전행렬의 성분 해당하는 벡터는 반드시 서로 정규직교 하여야 하므로 필요한 경우 확인 후 정규화하여 사용해야 함에 유의한다.
4. 실험 결과
4.1. 실험환경
자세 추정 실험 환경을 구성하기 위해서는 추정된 자 세를 검증하기 위해 기준이 될 수 있는 정확한 자세 정보 가 필요하다. 이를 위해 고가의 자세 추정 센서와 정밀하 게 제작된 기구부가 필요하다. 또한 카메라를 이용한 자 추정 결과는 카메라의 제조 공정상 발생하는 센서의 정 렬문제, 센서 픽셀의 크기 편차, 렌즈에 의한 왜곡 정도 에 영향을 받는다. 그리고 제안하는 방법의 경우, 사각형 특징 추출 방법의 성능에 따라 자세 추정 결과에 상당한 영향을 줄 수 있다.
위와 같은 오차 요인을 분리하여 자세 추정 알고리즘 만의 성능을 분석하기 위해 시뮬레이션 환경을 구성하 였다. 시뮬레이션은 로봇용 공개 시뮬레이터인 Gazebo 를 이용하였다.
실험 환경 구성은 Fig. 4에 묘사되어 있다. 사용하는 직사각형은 297×210 mm의 크기를 가진다. 카메라는 투 명하게 처리된 경위대식 기구부의 말단에 고정되어 있 으며 시뮬레이터의 원점을 중심으로 하는 반구의 표면 위에서 동작한다. 영상의 크기는 640×480 픽셀이고 카 메라의 Field of View는 100도로 설정하였다. 또한 카메 라는 렌즈왜곡, 화상 잡음을 포함하지 않도록 하였다.
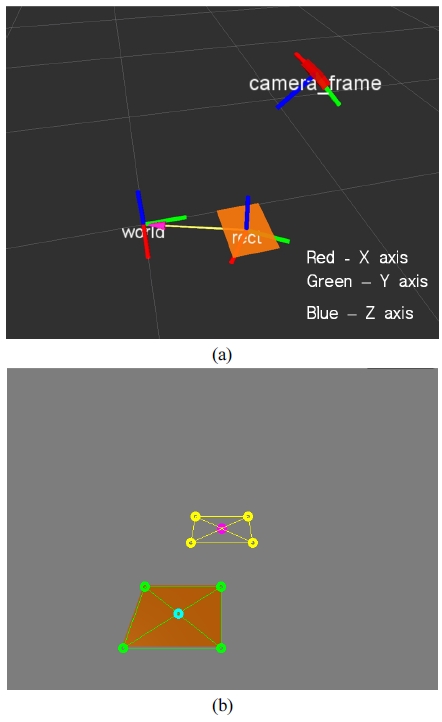
The configuration of the camera and the feature for the simulation (a) and extracted temporal quadrilateral (b)
사각형의 추출 알고리즘에 대한 의존성을 분리하기 위해 사각형은 핀홀 카메라 모델과 시뮬레이터에서 제 공하는 직사각형 중심의 ground truth위치를 이용하여 카메라에 투영되는 사변형을 추출하였다.
4.2. 실험결과 및 분석
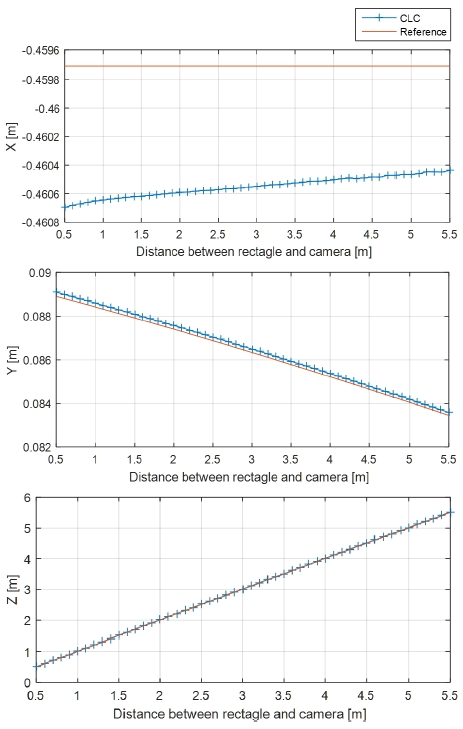
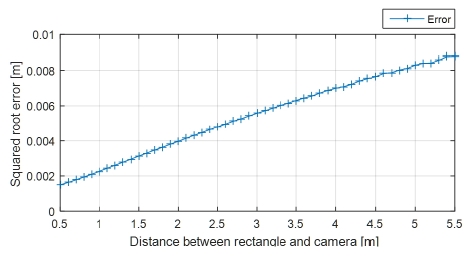
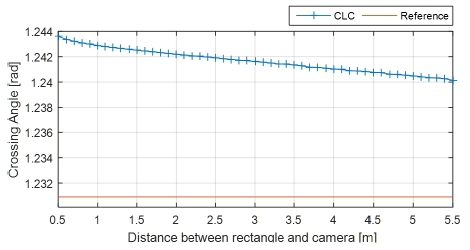
제안하는 자세 추정 방법의 정확도 분석을 위해 두가 지 실험을 구성하였다. 첫 번째 실험은 경위대의 위도와 거리를 각각 0.7 rad, 1 m로 고정하고 경도를 0.4 rad부터 0.1 rad씩 6 rad까지 회전하는 실험을 구성하였다. 두 번 째 실험은 두 물체 사이의 거리를 0.5 m부터 5.5 m까지 0.1 m씩 증가하며 자세추정 결과를 확인한다.
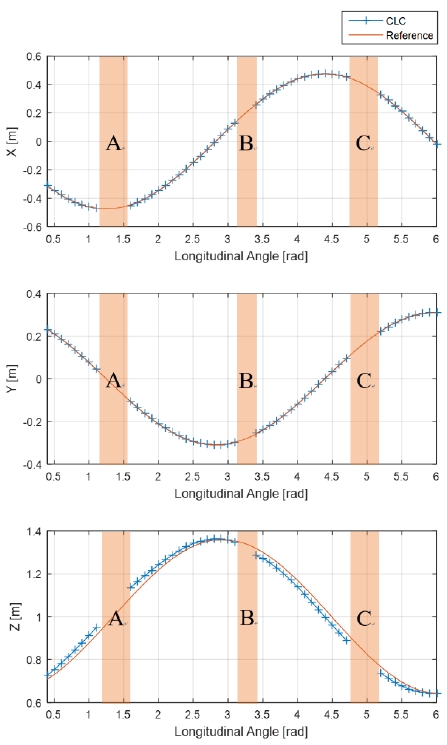
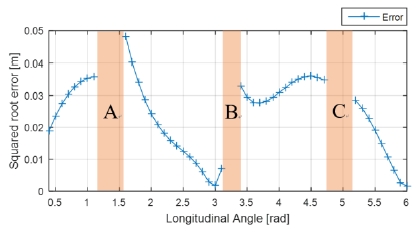
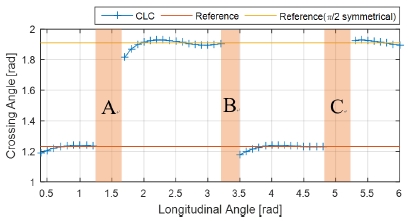
Fig. 5와 Fig. 8에서는 시뮬레이터에서 얻을 수 있는 카메라와 특징 사이의 기준 자세와 제안한 방법으로 얻 어낸 자세 추정 결과를 각각 거리변화와 회전량 변화에 대해 비교한 그래프이다. Fig. 6과 Fig. 9는 기준 자세와 제안한 방법을 이용해 얻은 자세의 square root error를 각각의 실험에 대해 계산한 그래프이고, 마찬가지로 Fig. 7과 Fig. 10은 각각의 실험에 대해 선분카메라쌍을 이용 한 사각형 복원 알고리즘의 종횡비 추출 결과를 보여준 다. 추가로 Fig. 11은 회전량과 자세 추정 결과의 양상을 직관적으로 비교하고자 기준자세와 추정한 상대 자세를 3차원의 벡터로써 표현한 그래프이다.
실험에서 회전운동에 대해서는 최대 0.05 m의 오차를 보이고 있으며 카메라와 특징 사이의 거리에 대해서는 최고 5 m 차이를 가지고 있음에도 불구하고 자세 추정 오차는 최대 0.01 m 이하로 우수한 성능을 보이고 있음 을 알 수 있다.
Fig. 8, Fig. 9, Fig. 10 그래프에 음영으로 표현 된 회전 운동 시의 자세 추정 결과 그래프의 불연속 구간 A, B, C는 직사각형 복원 알고리즘이 결과를 내는 데 실패하여 정상적으로 사각형의 형태를 복원할 수 없는 경우이다. 또 이 불연속 구간 근방에서 자세 추정에 있어 실험 결과 가운데 가장 큰 오차를 보이고 있다. 주목할 점은 종횡비 추출 결과를 보인 그래프에서 종횡비가 불연속 구간과 함께 두 종류로 구분되는 결과값을 보인 것을 확인할 수 있다. 두 개의 서로 다른 종횡비 값은 서로 π/2에 대해 대칭관계에 있음을 알 수 있고 이는 직사각형이 π/2 전후로 회전하면서 종횡비가 예각과 둔각으로 각각 표현되는 것에 기인한다고 파악할 수 있다. 이는 자세 추정에서는 0.05 m 이하의 미약한 오차만을 보여주고 있어 용인할 수 있으나, 향후 종횡비를 직사각형 특징의 단일 기술자로써 사용하고자 할 때 회전한 동일 특징에 대해 구분이 불가능한 문제가 발생 할 수 있다고 판단된다.
5. 결 론
본 논문에서는 사각형 특징을 이용하는 Visual SLAM 을 위해 perspective 변환에 의해 왜곡된 직사각형을 복 원하는 알고리즘과 호모그래피를 이용한 자세 추정 방 법을 응용하여 메트릭 공간에서의 특징과 카메라 간의 상대 자세 추정 방법을 제안하고 시뮬레이션을 이용한 실험에서 카메라의 회전과 천이에 대한 자세 추정의 정 확성을 정량적으로 분석하였다.
이 방법에서는 복원된 직사각형을 입력으로 카메라의 자세를 추정하게 되므로 입력 사변형에 대한 직사각형 복원의 정확도에 따라 자세 추정의 성능이 차이를 보이 게 된다. 그러나 실험에서 볼 수 있듯이 제안하는 방법을 이용한 카메라의 상대 자세 추정에 대한 오차는 기준 자세와 비교하여도 미미한 수준으로 실험 환경과 같이 정확한 사변형의 꼭지점이 주어졌을 경우에는 여타 시 각 특징 기반 자세 추정 알고리즘에 비해 구조가 간단하 면서도 높은 성능을 낼 수 있음을 보였다. 향후 연구에서 는 강인하고 정확한 사각형 추출 알고리즘과 통합하여 추출된 영상 내의 특징과 추정한 자세 사이의 오차를 모델링하여 효율적인 Visual SLAM을 개발할 것이다.
Notes
References
-
DeSouza, GN, Kak, AC, “Vision for mobile robot navigation: A survey”, IEEE Trans. Pattern Analysis and Machine Intelligence, (2002), 24(2), p237-267.
[https://doi.org/10.1109/34.982903]

-
Heo, H, Song, JB, “Global localization based on ceiling image map”, J. of Korea Robotics Society, (2014), 9(3), p170-177.
[https://doi.org/10.7746/jkros.2014.9.3.170]

-
Lategahn, H, Geiger, A, Kitt, B, “Visual SLAM for autonomous ground vehicles”, IEEE Int’l Conf. on Robotics and Automation, (2011), p1732-1737.
[https://doi.org/10.1109/icra.2011.5979711]

-
Strasdat, H, Montiel, J, Davison, A J, “Real-time monocular SLAM: Why filter?”, IEEE Int’l Conf. on Robotics and Automation, (2010), p2657-2664.
[https://doi.org/10.1109/robot.2010.5509636]

-
Davison, AJ, Reid, ID, Molton, ND, Stasse, O, “MonoSLAM: Real-time single camera SLAM”, IEEE Trans. Pattern Analysis and Machine Intelligence, (2007, June), 29(6), p1052-1067.
[https://doi.org/10.1109/tpami.2007.1049]

-
Klein, G, Murray, D, “Parallel tracking and mapping for small AR workspaces”, 6th IEEE and ACM Int’l Symposium on Mixed and Augmented Reality, (2007).
[https://doi.org/10.1109/ismar.2007.4538852]

-
Hong, SH, Kim, JW, “Visual SLAM using local bundle optimization in unstructured seafloor environment”, J. of Korea Robotics Society, (2014), 9(4), p197-205.
[https://doi.org/10.7746/jkros.2014.9.4.197]

-
Takezawa, S, Herath, DC, Dissanayake, G, “SLAM in indoor environments with stereo vision”, IEEE/RSJ Int’l Conf. on Intelligent Robots and Systems, (2004), p1866-1871.
[https://doi.org/10.1109/iros.2004.1389669]

-
Tardif, JP, Pavlidis, Y, Daniilidis, K, “Monocular visual odometry in urban environments using an omnidirectional camera”, IEEE/RSJ Int’l Conf. On Intelligent Robots and Systems, (2008), p22-26.
[https://doi.org/10.1109/iros.2008.4651205]

-
Kerl, C, Sturm, J, Cremers, D, “Dense visual SLAM for RGB-D camera”, IEEE/RSJ Int’l Conf. on Intelligent Robots and Systems, (2013), p2100-2106.
[https://doi.org/10.1109/iros.2013.6696650]

-
Nistér, D, “Preemptive RANSAC for live structure and motion estimation”, Machine Vision and Applications, (2005), 16(5), p321-329.
[https://doi.org/10.1007/s00138-005-0006-y]

-
Silveira, G, Malis, E, Rives, P, “An Efficient Direct Approach to Visual SLAM”, IEEE Trans. Robotics, (2008), 24(5), p969-979.
[https://doi.org/10.1109/tro.2008.2004829]

-
Engel, J, Sch, T, Cremers, D, “LSD-SLAM: Large-Scale Direct Monocular SLAM”, European Conf. on Computer Vision, (2014), p1-16.
[https://doi.org/10.1007/978-3-319-10605-2_54]

-
Lu, Y, Song, D, Yi, J, “High Level Landmark-Based Visual Navigation Using Unsupervised Geometric Constraints in Local Bundle Adjustment”, IEEE Int’l Conf. on Robotics and Automation, (2014), p1540-1545.
[https://doi.org/10.1109/icra.2014.6907056]

- Lee, J, “Camera calibration from a single image based on coupled line cameras and rectangle constraint”, 21 st Int’l Conf. on Pattern Recognition, (2012), p758-762.
- Hartley, R, Zisserman, A, Multiple View Geometry in Computer Vision, (2003), Cambridge University Press.
-
Lee, J, “New Geometric Interpretation and Analytic Solution for Quadrilateral Reconstruction”, (2014), 22nd Int’l Conf. on Pattern Recognition, p4015-4020.
[https://doi.org/10.1109/icpr.2014.688]