Kinect센서를 이용한 물체 인식 및 자세 추정을 위한 정확도 개선 방법
†Corresponding author: Mechanical Engineering, SungKyunKwan University, Chunchun-Dong, Jangan-Gu, Suwon, Korea ( hrchoi@me.skku.ac.kr)
© Korea Robotics Society All rights reserved
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents a method of improving the pose recognition accuracy of objects by using Kinect sensor. First, by using the SURF algorithm, which is one of the most widely used local features point algorithms, we modify inner parameters of the algorithm for efficient object recognition. The proposed method is adjusting the distance between the box filter, modifying Hessian matrix, and eliminating improper key points. In the second, the object orientation is estimated based on the homography. Finally the novel approach of Auto-scaling method is proposed to improve accuracy of object pose estimation. The proposed algorithm is experimentally tested with objects in the plane and its effectiveness is validated.
Keywords:
Object Recognition, Object Pose Estimation, Kinect Sensor1. 서 론
로봇이 3차원 공간에서 작업을 수행하기 위해서는 물체 환경 인식이 중요하며 시각 센서인 카메라를 활용한 물체 인식 및 자세 추정에 관한 연구가 로봇 분야에서 활발히 진행되고 있다[1-4]. 또한 최근 Microsoft 사에서 개발된 Kinect는 저렴한 가격과 작은 크기로 이러한 연구의 확대에 기여하고 있다[5,6]. 하지만 Kinect는 고가의 성능이 좋은 장비와 비교할 때 정확도가 떨어진다. 이런 부정확성은 로봇을 조작하여 대상 물체와 작업을 수행할 때, 특히 파지 동작에서 문제를 야기한다. 그러므로 Kinect를 이용하여 로봇이 물체를 조작하기 위해서는 정확한 물체 인식과 위치 및 자세 추정이 선행되어야 한다. 이 논문에서는 Kinect를 활용할 때 발생하는 카메라의 오차 보정과 정확도를 향상시키기 위한 새로운 기법을 제안하고자 한다.
Kinect는 원래 게임용으로 개발된 컨트롤러로 원래 사람의 몸이나 손을 인식하고 추적하기 위한 장치이다. 따라서, 외부 변수가 많은 실외 환경보다는 실내 환경에서 사용이 적합하며, 측정거리가 짧고 잡음이 심한 단점이 있다. 그러므로 Kinect에 관한 연구의 대부분은 사람의 제스처나 움직임을 인식하는 분야에서 활발히 진행되고 있다.
A. Weiss 외 2인은 사람의 실루엣을 기반으로 3차원 점군들에서 생기는 오차 범위에 대해 최적화 하는 연구를 진행하였으며, RGB의 윤곽선만 사용했을 경우 최대 약 8cm의 오차를 RGB와 depth를 동시에 사용하였을 경우 최대 약 6cm의 오차로 줄일 수 있었다[7]. I. Oikonomidis 외 2인은 사람 손을 추적하기 위한 용도로 Kinect를 사용하였고 5m에서 평균 5mm의 오차와 2.5m 부근에서는 7.5mm의 오차가 발생하며 손 위치의 오차 범위가 최소 5mm에서 최대 25mm 사이가 발생한다고 하였다[8]. 또한, Kinect의 잡음으로 인하여 정확한 데이터를 얻기 어려워 Kinect 보정과 영상 필터에 관한 연구가 필요하게 되었다. K. Khoshelham 외 1인은 Kinect의 해상도는 거리가 멀어질수록 적외선 패턴 간의 거리가 조밀해지지 못해 정확도 높은 데이터를 얻기 어려워 Kinect를 1-3m 사이에 사용시 적합하다고 하였으며, 오차 보정 후 5m 거리에서 최대 7cm의 오차가 발생한다고 하였다[9].
사람의 몸이나 손과 같이 신체 일부분을 인식할 경우, 일상 생활에 사용하는 물체보다 영상 평면에서 차지하는 표면적이 넓기 때문에 전체 영상에서 차지하는 비율이 높게 된다. 일반적으로 영상에서 목표로 하는 대상의 영역이 많이 포함되어 있을수록 인식률은 높아진다. 하지만, 일상 생활 속 물체를 인식하기 위해 Kinect를 사용하는 경우 물체가 영상 평면에서 차지하는 비율이 낮아 물체 인식이 어렵다.
따라서, 본 연구에서는 특징점 알고리즘 중 하나인 SURF(Speeded Up Robust Feature) 알고리즘을 이용하여 물체를 인식하고[10], 호모그라피를 이용해 평면 기반의 위치 및 자세추정을 진행한다. 이 과정에서 기존 SURF 알고리즘의 내부 변수를 수정해 속도와 정확도를 향상 하며, 기존의 방법인 RGB 정보만을 이용한 호모그라피 대신 depth 정보를 활용하여 기준영상의 크기를 자동으로 조정하는 기법인 오토스케일링 기법(Auto-scaling)을 통해 물체의 위치와 자세 추정의 정확도를 향상시킬 수 있는 알고리즘을 제안하고자 한다. 아울러 동 알고리즘을 실제 시스템에 구현하여 실효성을 입증하고자 한다.
2. 물체 인식
SURF 알고리즘은 SIFT(Scale-invariant feature transform) 알고리즘[11]에서 가장 문제가 되었던 속도를 개선한 알고리즘이다. 하지만 SURF 알고리즘만으로 물체를 인식 하고 실시간 로봇 조작하기에는 인식률과 속도면에서 한계가 있다.
본 논문에서는 인식률과 속도 개선을 위해 SURF 알고리즘을 크게 변형하지 않고 사각 필터간 거리 조절, 헤시안 행렬의 값 조절, 잘못 측정된 값을 제거하는 방법을 사용하였다.
SURF 알고리즘은 적분영상으로 사각 필터를 만들어 적분 값을 계산하는데 수식 (1)과 같이 계산한다. 적분영상 I(X) 는 4개의 픽셀 값만을 사용하여 원점에서 각각의 위치 X = (x,y)T 에서 픽셀 값들을 합하여 사각형 영역을 계산한다.
| (1) |
수식 (1)에서 생성된 사각 필터에서 수식 (2)와 같이 근사화된 헤시안 행렬(Approximated Hessian matrix)을 이용하여 특징점을 추출한다.
| (2) |
여기서 X는 입력 영상 위치를 나타내며 Lxx (X,σ)는 입력 영상과 σ의 분산을 갖는 x방향의 가우시안의 2차 미분 값
사각 필터들의 크기를 증가하면서 특징점을 추출할 때, 사각 필터간 거리를 조절하면 후보 점들 중에서 최적의 특징점이 되는 범위를 선정한다. 첫 번째 사각 필터의 중심 픽셀을 Dcenter1 (xcent1, ycent1), 크기가 조절된 두 번째 사각 필터의 중심 픽셀을 Dcenter2 (xcent2, ycent2) 라고 하면 사각 필터간의 중심거리 Dist는 수식 (3)과 같이 나타낼 수 있다.
| (3) |
| (4) |
수식 (4)의 Distmin 과 Distmax 는 실험에 의해 결정되는 상수 값으로 이 값으로 인식 범위를 조절하여 인식 률을 향상시킬 수 있다.
속도 개선 방법으로는 수식 (2)의 결과 H값의 최소 범위를 높게 선정한다. H 값이 클수록 추출되는 특징점의 수는 적어지지만, 정확한 특징점의 후보들로 기존의 SURF 알고리즘보다 개선된 속도를 얻을 수 있다.
SUFR 알고리즘을 이용해 특징점을 검출할 때 부정확한 특징점도 함께 검출되는데 이는 물체 인식률을 떨어뜨리는 요인이 된다. 잘못 대응된 특징점의 경우 RANSAC (Random Sample Consensus) [12]을 사용하여 잡음이 심한 원본 데이터로 최소한의 특징점을 랜덤 샘플링하여 적절하지 않은 특징점을 제거하고, Brute Force로 정합을 수행한다. 이렇게 내부변수의 수정을 한 SURF알고리즘을 Modifed SURF라 부르도록 하겠다. Modified SURF 알고리즘에서 인식하고자 하는 물체의 정보가 담긴 화면을 기준 영상(reference image)이라 하며, Kinect에 입력 영상으로 보이는 화면을 용어의 혼재를 피하기 위해 현재 영상(scene image)이라 정의 한다.
3. 물체의 위치 추정 및 정확도 개선
3.1. 물체의 위치 추정
인식된 물체의 영역으로부터 물체가 놓여진 위치를 추정하기 위해서는 우선적으로 카메라의 보정이 필요하다. Kinect는 RGB 영상을 출력하는 카메라와 depth 영상을 출력하는 카메라가 있어 두 개의 카메라의 보정이 필요하다. 본 연구에서는 GML camera calibration tool을 사용해 보정을 수행하였고, 이를 통해 카메라의 좌표계를 도출하였다[13].
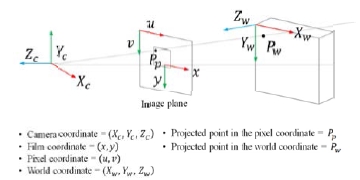
3차원 좌표계는 Fig 1.처럼 임의의 점 Pw = (Xw, Yw, Zw)T 이 놓여진 좌표계와 Kinect의 좌표계를 말한다. 점 Pw 가 놓인 좌표계를 월드 좌표계 (World coordinate)라 하고 (Xw, Yw, Zw) 로 나타내며, Kinect 좌표계를 카메라 좌표계(Camera coordinate)로 정의하며(Xc, Yc, Zc) 로 나타낸다. 월드 좌표계에서 카메라 좌표계로 회전 및 위치 변환 관계는 4 x 4 행렬로 나타나는데 이를 외부 파라미터(Extrinsic parameter)라 한다. 이때, R은 3×3 회전변환 행렬이고 t는 3×1 이동변환 벡터를 뜻한다.
점 Pw 은 2차원 영상 평면(Image plane)의 점 Pp = (u,v)T 로 대응되는데, 카메라 좌표계와 초점거리 f 만큼 떨어져 있는 지점에 위치한다. 편의상 Fig. 2에서는 픽셀 좌표계(Pixel coordinate)인 (u,v와 필름 좌표계(Film coordinate)인 (x,y)을 가상의 평면인 영상 평면에 같이 표현하였다.
3차원 Pw 점에서 2차원 Pp 점으로 투영 변환을 나타내면 수식 (5)와 같고, K는 내부 파라미터(Intrinsic parameter)로 3×3 행렬로 표현되며 초점거리 (fx, fy) 와 주점 (cx, cy) 을 포함하고 있다.
| (5) |
물체의 위치와 자세는 외부 파라미터에 의해 구해지므로, 호모그라피를 이용한 외부 파라미터를 계산하였다[14]. 호모그라피란 3차원 공간에 존재하는 2차원 평면을 2차원 영상 정보로 사상(Mapping)하는 것을 말한다.
즉, 3차원 물체에 대한 정보는 카메라 입력 영상에서 u,v의 2차원 좌표로 표현된다. 2절에서 인식한 물체의 평면과 기준 영상의 평면 간의 대응 관계를 통해 호모그라피를 이용한 물체의 위치와 자세를 추정할 수 있으며 수식 (5)의 내부 파라미터와 외부 파라미터는 [15]의 호모그라피의 정리에 의해서 3×3 행렬의 호모그라피 H = [h1 h2 h3] 로 나타낼 수 있다.
| (6) |
| (7) |
| (8) |
| (9) |
| (10) |
여기서 λ 는 크기의 인자로 λ = 1/∥K-1h1 ∥ = 1/∥K-1h2 ∥ 이다. r1 과 r2 는 수식 (7), (8)와 같이 구할 수 있으며 r3 은 r1 과 r2 에 의해 다시 계산된다. t의 경우는 수식 (10)와 같이 계산할 수 있으며 이로써 외부 파라미 터를 얻을 수 있게 된다.
3.2. 호모그라피 보정
호모그라피를 이용하여 외부 파라미터를 계산하고, 이를 통해 물체의 자세를 추정하기 때문에 호모그라피의 변형이 발생하는 경우 물체의 회전 방향과 이동 거리에 오차가 생긴다. 영상에서 보여지는 4개의 모서리 점과 물체의 외곽선이 평면 물체에 정확히 맞게 되면 Fig. 2(a)처럼 물체의 자세 추정이 정확하게 이루어 진다.
반면에 Fig. 2(b)와 같이 호모그라피의 일그러짐이 발생하면 제대로 자세 추정을 하지 못한다. 그러므로 수식 (11)처럼 전체 대응점 중에서 호모그라피에 가장 가까운 값 α 를 선택할 확률을 높게 조절한다. Pscene 는 전체 대응점 중에서 현재 영상에 대응된 점을 뜻하며, Pref 는 기준 영상에 대응된 점을 나타낸다.
| (11) |
α 로부터 새로 계산된 대응점 NPscene, NPref 으로부터 호모그라피를 다시 계산 하고, 이 결과로 얻어진 호모그라피가 Hresult 이다. Kinect 영상의 미세한 흔들림에 의해 픽셀간 정확한 값을 얻을 수 없으므로 호모그라피의 민감도를 줄이기 위해 Hresult 를 N번 누적하여 평균 값을 낸 Hfinal 을 최종적으로 사용한다.
| (12) |
3.3. 오토 스케일링 기법
물체를 움직이게 되면 기준 영상과 현재 영상에 보여지는 물체의 크기가 달라지게 된다. 기준 영상과 현재 영상의 크기 차이만으로 Hfinal 의 오차가 많이 발생하는데 특히, 기준 영상의 크기가 현재 영상보다 더 커지는 경우 어파인 변환(Affine transform)만으로도 물체의 각도 오차가 크게 나타난다.
따라서, 기준 영상의 크기와 현재 영상에 보이는 물체의 크기를 같게 조절하면 각도 오차를 줄일 수 있다. 또한, 기준 영상의 크기 조절 시 RGB와 depth 정보를 이용하면 영상간 크기 조절을 안정적으로 할 수 있다.
이로 인해 호모그라피의 변형이 일어나는 것을 방지 할 수 있으며 물체를 움직이더라도 물체의 자세 추정 시 발생하는 오차를 크게 개선 할 수 있다. 이렇게 두 영상 간의 크기 조절을 하는 방법을 오토 스케일링(Auto-scaling)이라 정의하고 수행 과정은 다음과 같다.
- ① Hfinal 로 얻어진 물체의 모서리 4점 획득
- ② 획득한 4개의 모서리를 깊이 영상에 투영하여 물체의 넓이와 높이 계산
- ③ ②에서 계산된 물체의 정보로부터 기준 영상의 크기를 맞춤
- ④ 현재 영상의 물체가 움직이더라도 항상 ①~③ 번 과정을 반복하여 크기 조절
과정 ①에서 4점은 크기를 계산하는데 사용되는 최소한 점의 개수이고, 과정 ②는 조명변화에 민감한 RGB에 depth정보를 같이 활용하여 안정적으로 크기 계산을 할 수 있도록 한다. 과정 ③을 거치면 Fig. 3와 같이 실시간으로 기준 영상의 크기가 현재 영상의 크기에 맞게 조절된다.
특징점 알고리즘이 물체 인식에는 기본적으로 크기, 조명, 시점 변화에 강인하지만 자세 추정을 위해 호모그라피를 도출할 때는 두 영상간의 크기 차이가 발행하면 불안정한 호모그라피가 생성되어 부정확한 결과를 초래한다. 이는 어파인 변환이 크기 변화에 민감한 특징을 갖는다는 것을 예측할 수 있다. 따라서, 상위 개념인 투영 변환(Perspective transform)에서도 동일한 문제점이 작용한다. 이러한 문제점을 개선하기 위한 방법이 오토 스케일링 기법의 주된 목적이다.
4. 실험 및 결과
실험은 Fig. 4와 같이 총 3개의 크기가 다른 상자를 가지고 진행하였으며, Kinect가 깊이 값을 인식하는 범위인 800mm 이상인 지점에 물체를 놓고 실험을 하였다.
실험에 사용된 컴퓨터 사양은 Intel Core i5 760 CPU, 4 GB RAM, NVDIA GeForce GT 220과 4GB memory이며, Table 1의 변수 값에 의해 실험을 진행하였다.
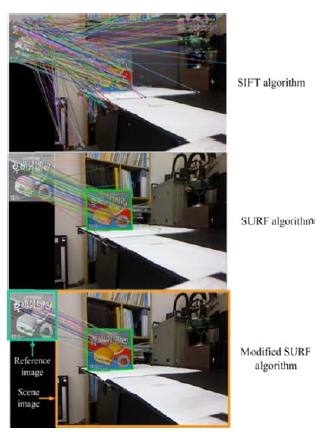
Fig 5.는 3개의 알고리즘을 비교한 그림이다. SIFT 알고리즘은 많은 특징점으로부터 물체를 인식하기 때문에 SURF 알고리즘에 비해 기준 영상과 현재 영상에서 보여지는 특징점의 수가 많다. 반면 SURF 알고리즘의 경우 SIFT 알고리즘에 비해 특징점의 수가 적은 특징을 볼 수 있다. Modified SURF 알고리즘 역시 SURF 알고리즘처럼 적은 특징점으로 물체 인식을 하며, 오정합된 특징점이 SURF에 비해 현저히 낮다는 것을 육안으로 확인 할 수 있다.
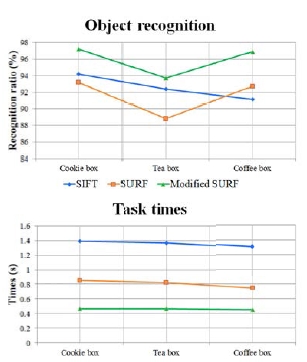
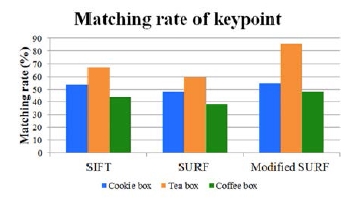
물체 인식률에 관한 실험은 Fig. 6과 같이 물체의 종류에 따라 인식률이 달라지지만, 제안한 알고리즘이 95.944%의 인식률로 SURF 알고리즘의 91.567% 인식률과 SIFT 알고리즘의 92.567% 인식률에 비해 높은 인식률을 가지며, 기준 영상과 현재 영상간의 특징점 정합을 나타내는 정합률 역시 제안한 알고리즘이 기존의 알고리즘보다 높은 정합률을 가지고 있음을 Fig. 7에서 확인할 수 있었다. 물체 인식의 계산 시간도 0.458초로 SURF 알고리즘의 0.805초와 SIFT의 1.360초에 비해 개선된 속도를 확인 할 수 있다.
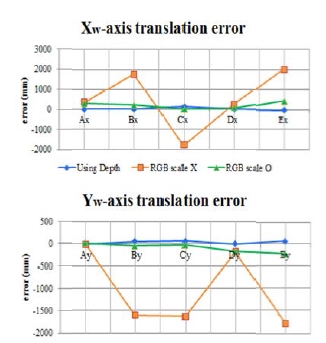
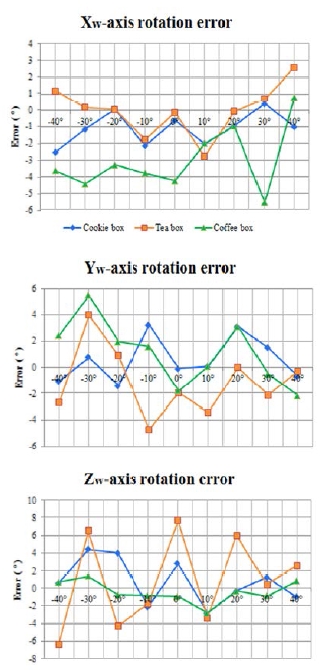
물체의 자세 추정은 modified SURF 알고리즘을 이용해 물체 인식을 한 후 진행되었으며 물체의 이동 시 오차는 월드 좌표계에서 A에서 G까지 Table 2와 같이 6개의 구간을 나누어 실험을 진행하였고, Table 2에서 기준이 되는 지점과 물체를 이동 했을 때의 비교 결과를 Fig. 8과 같이 나타내었다. 호모그라피의 보정과 오토 스케일이 포함된 결과에서 Xw 축 오차는 18.72cm, Yw 축은 8.80cm의 오차로 특히 RGB만을 사용하여 기준 영상의 크기 조절을 하지 않았을 때 Xw 축으로 50.65cm, Yw 축으로 103.94cm의 오차가 발생하였다. 또한, 물체를 Yw 축을 기준으로 10° 간격으로 ±40 ° 사이의 각도를 회전 하여 추정한 각도 값의 오차는 Fig. 9와 같다. 이 때 최대 오차가 약 8°이고 평균 3° 이내로 제안하는 알고리즘의 유용성을 입증하였다.
5. 결 론
본 논문에서는 기존 SURF 알고리즘의 내부 변수와 정합 필터를 강화하여 사각 필터간 거리 조절, 헤시안 행렬 값의 조절, 부정확한 대응 점의 제거로 인해 물체 인식의 속도 개선과 인식률을 높여 강건한 물체 인식이 가능한 알고리즘을 제안하였다. 물체의 위치와 자세 추정 시 변형이 심한 호모그라피를 보정하기 위해 호모그라피에 가까운 값을 선택할 확률을 지정한 후 N번의 호모그라피 값을 누적하여 호모그라피의 민감도를 줄였다. 또한, 오토 스케일링 기법으로 물체의 자세 추정 시 생기는 오차를 줄여 본 연구의 유용성을 입증할 수 있었다. 향후 다양한 형상의 물체 인식에 적용하기 위한 알고리즘 개선이 진행될 예정이다.
Reference
-
Calinon, S, D’halluin, F, Sauser, E, Caldwell, D, Billard, A, Learning and reproduction of gestures by imitation: An approach based on hidden Markov model and Gaussian mixture regression, IEEE Robot. Autom. Mag, (2010), 17(2), p44-54.
[https://doi.org/10.1109/MRA.2010.936947]

- Tommaso, D.D, Calinon, S, Caldwell, D.G, A Tangible Interface for Transferring Skills - Using Perception and Projection Capabilities in Human-Robot Collaboration Tasks, International Journal of Social Robotics, Special Issue on Learning from Demonstration, (2012), p1-12.
-
Muelling, K, Kober, J, Peters, J, Simulating Human Table Tennis with a Biomimetic Robot Setup, Lect. Notes Comput. Sci, (2010), 6226, p273-282.
[https://doi.org/10.1007/978-3-642-15193-4_26]

-
Forte, D, Gams, A, Morimoto, J, Ude, A, On-line motion synthesis and adaptation using a trajectory database, Robot. Auton. Syst, (2012), 60(10), p1327-1339.
[https://doi.org/10.1016/j.robot.2012.05.004]

-
Jung, M.K, Song, J.B, Robust Global Localization based on Environment map through Sensor Fusion, Journal of Korea Robotics Society, (2014), 9(2), p96-103.
[https://doi.org/10.7746/jkros.2014.9.2.096]

-
Park, C.H, Howard, A.M, Telepresence Robotic Technology for Individuals with Visual Impairments Through Real-time Haptic Rendering, Journal of Korea Robotics Society, (2013), 8(3), p197-205.
[https://doi.org/10.7746/jkros.2013.8.3.197]

-
Weiss, A, Hirshberg, D, Black, M.J, Home 3D body scans from noisy image and range data, IEEE International Conference on Computer Vision, Computer Vision and Pattern Recognition, (2011), p1951-1958.
[https://doi.org/10.1109/ICCV.2011.6126465]

-
Oikonomidis, I, Kyriazis, N, Argyros, A.A, Efficient model-based 3D tracking of hand articulations using Kinect, British Machine Vision Conference, (2011).
[https://doi.org/10.5244/C.25.101]

-
Khoshelham, K, Elberink, S.O, Accuracy and Resolution of Kinect Depth Data for Indoor Mapping Application, Sensors, (2012), p1437-1454.
[https://doi.org/10.3390/s120201437]

- Bay, H, Tuytelaars, T, Gool, L.V, SURF: Speeded Up Robust Features, European Conference on Computer Vision, (2006), 3951, p404-417.
-
Lowe, D.G, Distinctive Image Features from Scale invariant Key Point, Int. J. Comput. Vis, (2004), 60(2), p91-110.
[https://doi.org/10.1023/B:VISI.0000029664.99615.94]

-
Fischler, M.A, Bolles, R.C, Random Sample Consensus: A Paradigm for Model Fitting with Appli-cations to Image Analysis and Automated Cartography, Commun. ACM, (1981), 24, p381-395.
[https://doi.org/10.1145/358669.358692]

- Graphics and Media Lab, website http://graphics.cs.msu.ru/en/node/909.
-
Zhang, Z, Flexible camera calibration by viewing a plane from unknown orientation, IEEE International Conference on Computer Vision, (1999), p666-673.
[https://doi.org/10.1109/ICCV.1999.791289]

- Malis, E, Vargas, M, Deeper understanding of the homography decomposition for vision-based control, Research Report INRIA Sophia-Antipolis, (2005).