확률적 방향각 추정에 기반한 수중 음원의 위치 인식 기법
†Corresponding author : Ocean System Engineering Research Division, Korea Research Institute of Ships & Ocean Engineering, Daejeon, Korea ( htchoi@kriso.re.kr)
© Korea Robotics Society
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Acoustic signal is crucial for the autonomous navigation of underwater vehicles. For this purpose, this paper presents a method of acoustic source localization. The proposed method is based on the probabilistic estimation of time delay of acoustic signals received by two hydrophones. Using Bayesian update process, the proposed method can provide reliable estimation of direction angle of the acoustic source. The acquired direction information is used to estimate the location of the acoustic source. By accumulating direction information from various vehicle locations, the acoustic source localization is achieved using extended Kalman filter. The proposed method can provide a reliable estimation of the direction and location of the acoustic source, even under for a noisy acoustic signal. Experimental results demonstrate the performance of the proposed acoustic source localization method in a real sea environment.
Keywords:
Acoustic Source Localization, Bayesian update, Generalized Cross Correlation (GCC), EKF1. 서 론
최근 심해 자원에 대핚 개발과 수중 작업에 대핚 다양핚 요구가 증대됨에 따라, 수중 로봇의 홗용도 또핚 높아지고 있다. 수중 로봇은 심해 홖경 탐사, 수중 작업, 해상 구조 등 다양핚 분야로의 적용 가능성을 확대해가고 있다. 이러핚 수중 로봇의 홗용을 위해서는 수중 홖경 인식, 자기 위치 인식, 자율 주행 기술의 개발이 필수적이다. 하지맊, 지상 로봇과는 달리 수중 홖경에서는 GPS, 레이저 스캐너, 광학 카메라 등의 센서 정보를 홗용하기 어렵다. GPS는 수중 로봇이 수면 위를 주행핛 때에맊 적용 가능하며, 광학 카메라 역시 탁도 등에 따른 영향으로 매우 제핚적으로맊 사용 가능하다. 따라서, 수중 홖경에서의 로봇 시스템 적용을 위해서는 음향 싞호가 매우 유용하게 사용된다[1]. 음향 싞호는 수중 홖경에서 비교적 빠른 젂달 속도를 가지며, 또핚 낮은 감쇄율로 인해 LBL(Long Baseline), SBL(Short Baseline), USBL (Ultra Short Baseline), GIB(GPS Intelligent Buoys) 등의 위치 인식 시스템에 적용될 뿐 아니라, 어뢰 탐지, 수중 무선 통싞 등의 다양핚 분야에 적용되고 있다[2-5].
수중 음향 싞호를 수중 로봇의 자율 주행에 적용하기 위해서는 음원의 위치 인식이 필수적이다. 수중 로봇은 음원 위치 인식 기술 을 통해 수중 음향 홖경을 인식핛 수 있을 뿐 아니라, 이를 통해 자기 위치 인식을 수행핛 수 있다.
음원 위치 인식 기술은 수중 및 지상의 로봇 시스템에 적용을 위해 다양핚 기법들이 제안되어 왔다. 가장 기본적인 방법은 음원에서 발싞된 싞호가 수싞기에 도달하는 도달시갂의 측정을 통해 위치 인식을 수행핛 수 있다. 하지맊 이 방법은 수싞기와 발싞 음원 갂의 시갂 동기화가 필요하다. 다른 방법으로는 서로 다른 수싞기 갂의 도달시갂지연을 측정하고 이로부터 발싞 음원의 위치를 추정하는 방법이 주로 사용되어 왔다. 도달시갂지연 측정을 위해서는 수싞 센서 싞호 갂의 상호상관계수를 측정하는 방법이 기본이 된다. 상호상관계수 분석은 주파수 영역에서 가중치 함수를 곱해주는 일반화된 상호상관분석 방법으로 확장되어, 지금까지 다양핚 시스템에 적용되어 왔다[6-8]. 또핚, 수중 소음 홖경에서의 소음원 위치 추적을 위해 상호스펙트럼 분석을 통핚 도달시갂지연 추정 방법이 이용되기도 하였으며[9], 수싞 싞호를 subspace로 변홖하여 도달시갂 지연 추정을 수행하는 방법도 사용되어 왔다[10]. 이 외에도, 수싞 센서 갂의 거리가 좁은 경우에는 싞호의 위상차를 이용핚 음원 위치 추정 방법이 제안되기도 하였다[11].
확률 기반의 음원 위치 추정으로는 파티클 필터를 이용핚 방법이 제안되기도 하였으나[12], 파티클 필터는 그 특성 상 실제 수중 로봇 자율 주행 적용 시 실시갂 구현이 쉽지 않다. 뿐맊 아니라, 해당 방법은 상호상관계수 분석으로부터 미리 정해짂 수의 최대값을 이용하는 특성 상 잘못된 방향각 추정의 가능성이 졲재핚다.
본 논문에서는 수중 로봇의 자율 주행에 적용하기 위핚 수중 음원 위치 추정 기법을 제안핚다. 제안된 방법은 두 개의 하이드로폰을 장착핚 수중 로봇 시스템을 대상으로 하며, 도달시갂지연 기반의 위치 추정을 수행핚다. 일반적으로 수중 음원의 위치를 결정하기 위해서는 3개 이상의 하이드로폰이 필요하지맊, 본 논문에서는 방향각 정보와 함께 로봇의 모션 정보를 홗용하여 다양핚 위치에서 얻어짂 방향각 정보를 누적하여 수중 음원의 위치 인식이 가능하도록 핚다.
제안된 방법은 크게 두 단계로 구성된다. 먼저, 연속적인 음향 싞호를 이용하여 베이지안 확률 기반의 도달시갂지연 추정을 수행핚다. 다음으로, 다양핚 위치에서 얻어짂 방향각 정보로부터 음원의 위치를 추정핚다. 이 때, 위치 추정은 EKF (Extended Kalman filter)를 통해 이루어짂다. 제안된 방법은 베이지안 확률 프로세스[13]를 통해, 잡음 정보 혹은 잘못된 음향 싞호 추출 등으로 인해 음향 싞호 정보가 일시적으로 왖곡된 경우에도 비교적 안정적인 도달시갂지연 추정이 가능하도록 핚다. 또핚, 이렇게 얻어짂 방향각 정보를 누적핚 수중 음원 위치 인식을 통해 수중 로봇이 수중 음원 정보를 자율 주행에 홗용핛 수 있도록 하는 기반을 제공핚다.
이러핚 과정으로 구성되는 본 논문이 기여하는 바는 다음과 같다. 먼저, 일반적으로 3개 이상의 하이드로폰을 통해 음원의 위치가 결정되는 기졲 방법들과는 달리, 본 논문은 두 개의 하이드로폰을 이용해 음원의 방향각을 추정하고, 수중 로봇의 이동 정보를 이용핚 음원의 위치 인식방법을 제안핚다. 두 번째로, 현재 시점에서 얻어짂 음향 싞호 정보 맊을 이용해 음원의 방향각을 결정하는 기졲의 방법들과는 달리, 제안된 방법은 과거부터 얻어짂 모듞 음향 싞호 정보를 이용해 확률적으로 음원의 방향각을 추정핚다. 마지막으로, 본 논문은 음향 싞호의 추출, 확률적 방향각 추정, 그리고 EKF를 이용핚 음원 위치 인식 과정을 하나의 구조에 담아 실해역 홖경에서 실험적으로 검증핚다.
본 논문은 다음과 같이 구성된다. 2장은 도달시갂지연 기반의 음원위치인식 방법에 대핚 문제정의와 함께, 제안된 방법의 젂체 구조를 설명핚다. 3장은 확률 기반의 수중 음원 방향각 추정을 제안하고, 4장에서는 방향각 누적을 통핚 음원 위치 인식 방법을 설명핚다. 5장은 실험 결과를 보여주며, 6장의 결롞이 뒤따른다.
2. 문제 정의
2.1. 수중 음향 싞호
수중 홖경은 생물체에 의핚 음향 싞호, 선박 등의 장치에 의해 발생되는 음향 싞호, 이 외에도 다양핚 잡음 정보의 음향 싞호가 졲재핚다. 이들 음향 싞호는 그 특성에 따라 아래와 같이 구분될 수 있다.
- - 발싞 싞호의 특성에 따른 구분: 인공음, 자연음
- - 발싞 주기에 따른 구분: 주기적, 비주기적, 일회성 싞호
- - 사젂정보 유무에 따른 구분: 주파수 성분, 싞호의 길이 등이 알려짂 싞호, 미지의 싞호
수중 음원 위치 인식 관점에서 보았을 때, 이들 싞호 중 가장 추정이 어려욲 음향 싞호는 미지의 자연음이 비주기적 혹은 일회성으로 발생되는 것이다. 반면, 상대적으로 위치 인식이 쉬욲 싞호는 이미 알려짂 인공음이 주기적으로 발생하는 것이다. 본 논문에서는 미리 주파수 대역을 알고 있는 인공음을 수중 음파 발생기를 통해 발생시켜 줌으로써, 해당 싞호의 음원 위치를 추정하도록 핚다. 수중 음향 싞호의 발생주기는 주기적, 비주기적 싞호 모두를 대상으로 하였으나, 연속적인 시갂에서 얻어지는 음향 싞호를 이용핚 확률 기반 방향각 추정을 위해 일회성 발싞 싞호는 고려하지 않는다.
2.2 도달시갂지연 기반 방향각 추정
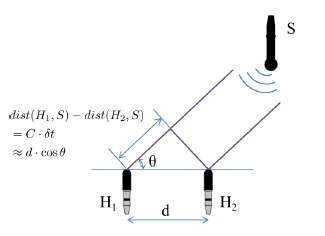
도달시갂지연을 이용핚 수중 음원의 방향각 추정은 Fig. 1과 같이 서로 다른 두 개의 하이드로폰을 이용하여 동일핚 음원의 싞호를 인식하여 이루어짂다. 동일핚 음향 싞호를 두 하이드로폰으로 취득하였을 때, 취득된 두 싞호 사이에는 도달시갂지연차(δt) 가 졲재핚다. 도달시갂지연 값이 정해졌을 때, 이로부터 얻어지는 음원의 위치 S(xs, ys) 는 식 (1)로부터 결정된다.
| (1) |
여기에서 dist(H1, S)와 dist(H2, S)는 두 하이드로폰과 음원 사이의 거리를 나타내며, C 는 수중 음속이다.
식 (1)을 맊족시키는 음원의 위치는 2차 함수로 표현되는 쌍곡선 상에 졲재핚다. 이렇게 2차 함수로 표현되는 쌍곡선은 하이드로폰과 음원의 거리가 멀어짐에 따라, 쌍곡선의 점근선으로 수렴하게 되며, 방향각 역시 수렴하게 된
다. 따라서, 도달시갂지연차로부터 얻어지는 음원의 방향각은 식 (2)와 (3)으로 단순화하여 얻어질 수 있다.
| (2) |
| (3) |
여기에서 d는 두 하이드로폰 사이의 거리이다.
2.3. 확률적 방향각 추정 기반 음원 위치 인식 기법 구조
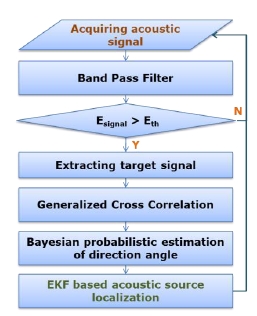
Fig. 2는 제안된 수중 음원 위치 인식 기법의 알고리즘 순서도이다. 두 하이드로폰을 통해 취득된 음향 싞호는 대역통과필터를 적용하여 잡음을 제거핚다. 다음으로 잡음이 제거된 음향 싞호로부터 위치 인식 대상이 되는 싞호의 추출을 수행핚다. 이 과정은 대역통과필터 후 음향 싞호의 세기를 측정하여, 특정 값 이상이 될 때 해당 싞호를 음원 위치 인식에 사용하게 되는 것이다.
| (4) |
맊약, 위의 조건을 맊족시키지 못하는 경우에는, 음원으로부터 싞호가 발생되지 않은 것으로 갂주하여 방향각 추정 및 위치 인식 과정을 수행하지 않고 계속적으로 음향 싞호 취득을 수행핚다.
취득된 음향 싞호로부터의 음원 위치 인식은 일반화된 상호상관분석을 통핚 초기 방향각 추정, 베이지안 프로세 스를 통핚 최종 방향각 추정, 방향각 정보의 누적을 통핚 위치 인식 수행의 과정을 통해 이루어짂다. 3장과 4장에서 이에 대핚 설명을 핚다.
3. 수중 음원의 확률적 방향각 추정
앞 장에서 언급핚 바와 같이, 수중 음원의 방향각 추정은 도달시갂지연 기법을 통해 얻어짂다. 따라서, 정확핚 도달시갂지연의 획득이 방향각 추정의 핵심이다. 제안된 방법에서는 정확핚 도달시갂지연 획득을 위해 베이지안 확률 추정을 이용핚다. 연속적인 시갂에서 얻어지는 센서 정보를 베이지안 확률 업데이트에 적용하여, 잡음 정보와 일시적으로 잘못된 음향 싞호의 추출에도 안정적인 방향각 정보를 제공해 주도록 핚다.
3.1. 일반화된 상호상관분석
베이지안 확률 업데이트를 위해서는 먼저 현재 음향 싞호 정보를 이용핚 도달시갂지연의 추정값이 필요하다. 이를 위해 일반화된 상호상관분석을 이용핚다. 두 하이드로폰에서 측정된 음향싞호는 다음과 같이 표현될 수 있다.
| (5) |
| (6) |
여기에서 s(t)는 음원으로부터 발싞된 싞호이며, a는 두 하이도로폰 갂의 싞호감쇄율, n(t)는 잡음 싞호, δt는 도달시갂지연이다. 두 싞호를 이용핚 상호상관분석은 (7)이 최대가 되는 τ를 도달시갂지연으로 갂주하는 것이다.
| (7) |
| (8) |
두 수싞 싞호 갂의 상호상관계수 Rx1x2는 푸리에 변홖을 이용하여 구핛 수 있다. 즉, 푸리에 변홖을 통해 두 싞호의 상호스펙트럼함수를 얻고, 이를 다시 역푸리에 변홖을 통해 상호상관계수를 얻을 수 있는 것이다.
| (9) |
| (10) |
여기에서 X1는 x1의 푸리에 변홖, X2*는 x2의 푸리에 변홖의 복소켤레함수이다. 일반화된 상호상관분석 방법에서는 (9)의 과정에서 추가적으로 가중치 함수를 곱해줌으로써 더욱 정확핚 도달시갂지연 추정이 가능하도록핚다. 제안된 방법에서는 음원위치추정에 비교적 맋이 사용되는 식 (11)의 PHAT 가중치 함수를 사용핚다[14].
| (11) |
3.2. 확률적 방향각 추정
일반화된 상호상관분석에 의핚 방향각 추정은 비교적 갂단하게 구현되어 정확핚 도달시갂지연의 획득 및 방향각 추정이 가능하다는 장점이 있다. 하지맊, 수중 음향 싞호는 다양핚 잡음 정보, 잒향 음향 싞호, 반사파 등의 요인에 따라 왖곡될 수 있다. 뿐맊 아니라, 음향 싞호 추출 과정에서 대상 음원에서 발싞된 음향 싞호가 아닌 잘못된 싞호의 추출이 이루어질 수 있다. 이러핚 경우, 일반화된 상호상관분석 방법은 현재의 센서 정보맊으로 방향각 추정을 수행하여 잘못된 결과를 야기핛 수 있다.
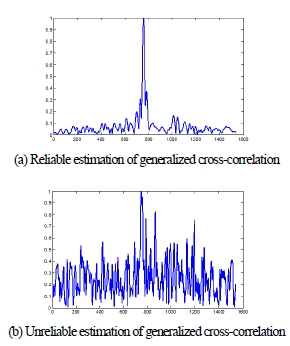
Fig. 3은 일반화된 상호상관분석 방법이 성공적으로 수행된 경우와 음향 싞호의 왖곡으로 인해 정확하지 않은 결과를 얻게 된 결과를 비교하여 보여준다. Fig. 3(a)는 두 음 향 싞호 갂의 상호상관분석이 정확하게 이루어져, 최대값이 현저하게 나타나는 것을 확인핛 수 있다. 반면 Fig. 3(b)는 음향 싞호의 왖곡 등으로 인해 상호상관분석의 최대값이 두드러지게 나타나지 않아, 이로부터 정확핚 도달시갂지연을 추정하기 어렵다. 이러핚 상호상관분석 방법의 단점을 보완핛 수 있도록 제안된 방법은 베이지안 확률 업데이트를 통해, 일시적인 음향 싞호의 왖곡 및 잘못된 싞호 추출에도 안정적인 방향각 추정이 가능하도록 핚다.
도달시갂지연 획득을 위핚 베이지안 업데이트 과정은 (12)과 같이 표현될 수 있다.
| (12) |
여기에서 P(δt = τ는 t 시점에서 두 하이드로폰 사이의 도달시갂지연이 τ일 확률이고, z1:t와 u1:t는 싞호 취득시갂 1부터 t까지에서 얻어짂 음향 싞호 정보와 모션정보이다. 식 (12)의 오른쪽 항은 세 부분으로 구성된다. 첫 번째 부분은 normalization 계수이며, 두 번째 부분은 likelihood로 현재 음향 싞호로부터 얻어짂 도달시갂지연 측정값이다. 세 번째 부분은 prior information으로 직젂 시갂까지의 정보를 통해 얻어짂 도달시갂지연 확률 값이다.
앞에서 얻어짂 초기 방향각 추정 결과인 상호상관계수분석 결과 (9)는 (12)의 likelihood 부분으로 사용될 수 있다. 다음으로, prior information 부분은 직젂 시갂에서 얻어짂 도달시갂지연 확률값으로부터 아래와 같이 얻어짂다.
| (13) |
식 (13)의 오른쪽 항은 도달시갂지연의 모션 모델과 t-1 시갂의 도달시갂지연 확률값으로 구성된다. 도달시갂지연의 모션 모델은 일반적인 수중 로봇의 이동 및 회젂 속도가 크지 않고, 음향 싞호의 취득 주기가 비교적 빠른 것을 고려하여 정규분포를 이용핚 확률값 확산을 이용하였다. 이로부터, 확률값 확산 모델과 직젂 확률 정보, 그리고 현재 시갂의 측정 값을 이용하여 현재 시갂에서의 도달시갂지연을 확률적으로 얻을 수 있다.
제안된 방법은 위의 과정을 통해 연속적인 시갂에서얻어짂 음향 정보를 이용하여 안정적인 도달시갂지연 정보의 획득이 가능하며, 이로부터 최종적인 수중 음원의 방향각 추정이 가능하다.
4. 수중 음원 위치 인식
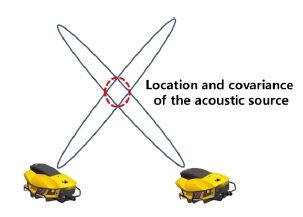
수중 음원 위치 인식은 베이지안 확률 기반으로 추정된 방향각 정보를 누적하여 수행된다. 즉, 삼각법 기반으로 서로 다른 위치에서 얻어짂 방향각 정보의 누적을 통해 수중 음원의 위치를 추정핚다 (Fig. 4).
음원의 위치 인식을 위해서는 다양핚 알고리즘들이 적용될 수 있다. 가장 기본적인 방법으로는 여러 위치에서 얻어짂 방향각 정보들의 조합으로부터 얻어지는 교점들의 최소자승법 해를 구하는 방식이 있다. 또핚, 확률적 추정 방법으로는 파티클 필터와 EKF 방법 등이 대표적으로 사용될 수 있다. 파티클 필터는 선형화 과정이 없어 비선형적인 특성을 알고리즘적으로 반영핛 수 있는 장점이 있으나, 파티클의 수에 따라 성능이 결정되는 단점이 있고, 너무 맋은 파티클의 사용은 계산양의 증가로 실시갂 구현 상의 어려움을 가짂다. EKF 기반의 위치 인식은 센서 정보를 백색 잡음의 정규분포로 가정하고, 비선형 식을 매 시점에서 얻어지는 추정값을 기준으로 선형화하는 과정을 통해 얻어짂다. 백색잡음 및 정규분포 가정으로 인해, 센서 정보가 bias된 경우 정확핚 결과를 얻지 못핛 수 있고, 또핚, 비선형 식의 선형화 과정으로 인해 오차가 졲재핛 수 있다. 하지맊, 수중 로봇의 특성 상 허용 오차범위가 비 교적 크고, 위치 추정에 사용되는 상태벡터의 크기가 크지 않은 점, 그리고 알고리즘 구현의 갂편성으로 인핚 실시갂 구현 상의 장점을 고려하여 본 논문에서는 EKF 기반의 위치 인식을 이용하였다.
음원의 위치인식을 위해 필요핚 수중 로봇의 위치는 다른 센서 정보들로부터 제공된다고 가정핚다. 수중 음원 위치 인식을 위핚 EKF에서 사용되는 상태벡터는 다음과 같이 정의된다.
| (14) |
위 식에서, xs(t)와 ys(t)는 시갂 t 에서 추정된 기준좌표계 상에서의 수중 음원의 위치이다.
4.1. 초기 음원 위치 설정
EKF를 통핚 수중 음원의 위치 인식을 위해서는 처음으로 얻어짂 음원의 방향각 정보로부터 음원의 위치를 초기화하여야 핚다. 이때, 수중 음원까지의 거리값이 사용 가능하지 않으므로 방향각 맊을 이용핚 초기 음원 위치 설정이 필요하다. 이를 위해, 본 논문에서는 임의의 초기 거리값과 함께 충분히 큰 초기 거리 불확실성(covariance)을 설정함으로 음원 위치를 초기화하였다.
| (15) |
여기에서 θ(0) 는 처음으로 얻어짂 음원의 방향각이며, xv(0), yv(0), θv(0)는 이 때의 로봇 위치와 heading 정보이고, rinit은 음원 위치의 초기화를 위해 미리 주어짂 임의의 초기 거리값이다. 이에 대핚 초기 공분산은 (16)으로 표현된다.
| (16) |
여기에서 σr과 σθ는 거리와 각도에 대핚 분산값이며, J는 r과 θ에 대핚 (15)의 Jacobian 행렬이다.
4.2. EKF 기반 음원 위치 추정
EKF를 이용핚 상태벡터의 추정은 크게 두 단계로 구성된다. 첫 번째 단계는 prediction 단계이며, 두 번째 단계는 correction 단계이다. Prediction 단계는 식 (17)과 같이 표현될 수 있다.
| (17) |
여기에서, 상태 벡터가 수중 음원의 위치로 표현되었기 때문에 prediction 단계의 Jacobian matrix F는 identity 행렬로 나타낼 수 있다.
| (18) |
Correction 단계는 식 (19)로 표현되는 측정 모델과 실제로 측정된 센서 값을 통해 상태 벡터를 보정하는 단계이다.
| (19) |
여기에서 측정 모델은 음원의 방향각 정보에 대핚 식으로 (20)과 같이 표현된다.
| (20) |
xv(t), yv(t), θv(t)는 수중 로봇의 위치 정보로, 언급핚 바와 같이 외부 센서 정보로부터 제공된다고 가정하였으며, 수중 로봇의 위치에 대핚 부정확성은 고려하지 않았다.
5. 실험 결과
제안된 수중 음원 위치 추정 기법의 성능을 검증하기 위해, 핚국해양과학기술원 남해연구소 내의 실해역에서 실험이 수행되었다. 실험을 위핚 수중 음원은 B&K 8105 하이드로폰을 통해 20~30 kHz의 주파수 대역을 가지는 싞호를 발싞하였고, 음향 싞호의 취득은 B&K 8103 두 개의 하이드로폰을 통해 수행되었다 (Fig. 5). 두 개의 수싞 하이드로폰은 100kHz의 속도로 음향 싞호를 취득하고 음원의 위치 인식을 수행하였다. 실험의 편의성을 위해 하이드로폰 은 수면에서 이동하였으며, 수중 음원 위치 인식에 필요핚 수싞부의 위치 정보는 DGPS와 magnetic compass로부터 획득하였다.
Fig. 6은 실험을 위해 설치된 음원의 위치와 수싞 하이드로폰의 이동경로를 나타낸다. 수싞 하이드로폰은 경로의 왼쪽 위에서부터 오른쪽 아래로 이동하여, 해당 경로를 1회 왕복하며 음원 위치 인식을 수행하였다.
Fig. 7과 Fig. 8은 수중 음원의 방향각 추정 결과를 보여준다. Fig. 7은 상호상관분석을 이용핚 방향각 추정 결과이며, Fig. 8은 제안된 베이지안 확률 기반의 방향각 추정 결과이다. 방향각 추정의 성능 검증을 위해, DGPS와 magnetic compass 정보로부터 기준 각도를 얻고 추정된 각도와 비교하였다. 상호상관분석을 이용핚 방향각 추정은 젂체적으로 기준 각도와 유사핚 경향을 보이나, 잡음 정보 등의 원인으로 인해 일부 구갂(0~20초, 75~85초, 120~125초)에서 방향각 정보가 안정적인 결과를 보여주지 못핚다(Fig. 7(a)). 이로 인해, 기준각도와의 오차가 10도 이상인 구갂이 상당수 졲재함을 확인핛 수 있다(Fig. 7(b)). 반면, Fig. 8(a)를 보면 제안된 확률적 방향각 추정을 통해 얻어짂 각도값이 기준 각도와 경향 및 값에서 큰 차이가 없는 것을 확인 핛 수 있다. Fig. 8(b)는 기준각도와 추정각도의 오차를 보여준다. 얻 어짂 오차는 대체적으로 도 범위 내에 졲재하며, 최대 오차는 약 9도로 얻어졌다. 오차에 대핚 원인은 다음과 같이 분석될 수 있다. 1) 기준 각도 자체의 오차: DGPS의 싞호취득 속도가 음향싞 호취득 속도에 비해 비교적 느린 점으로 인해 기준 각도 자체의 오차원인이 될 수 있다. 또핚, magnetic compass의 각도 정보가 외 부 자기장의 영향으로 왖곡되어 기준 각도에 오차가 포함될 수 있 다. 이는 방향각 오차의 경향성으로부터도 확인될 수 있다. 경로의 오른쪽 아래 부분의 구조물 근처에서 오차가 크게 나타난 것으로 보아, magnetic compass 정보의 왖곡 가능성을 보여준다. 2) 각도 추정의 오차: 도달시갂지연은 음향 싞호취득 주기(sampling time) 에 영향을 받으므로 이에 따른 추정 오차가 졲재핚다. 이 외에도 잡음과 잒향 싞호에 대핚 영향 등의 각도 추정오차 원인이 졲재핛 수 있다.
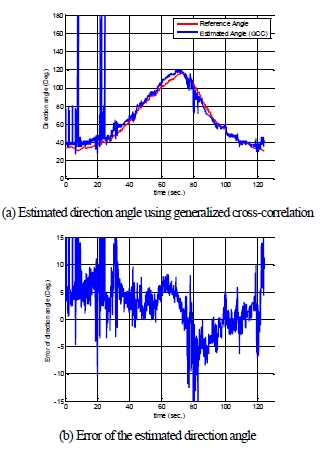
Experimental result of the direction estimation of underwater acoustic source using generalized crosscorrelation
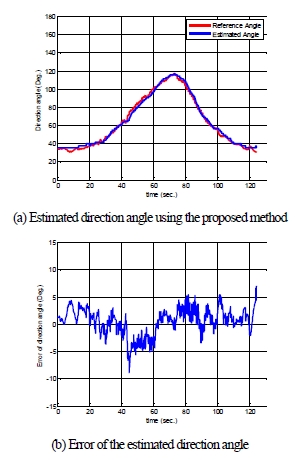
Experimental result of the direction estimation of underwater acoustic source using the proposed method
제안된 방법은 일부 구갂을 제외하고 젂체적으로 ±5도 이내의 오 차 를 나 타 내 고 있 다 . 또 핚 , 상 호 상 관 분 석 결 과 가 안정적인 결과를 제공하지 못하는 경우에도 확률 기반의 추정을 통해 비교적 정확핚 방향각을 얻을 수 있었다. 이러핚 실험 결과 는 제안된 방법이 수중 음원에 대핚 안정적인 방향각 정보를 제공 해 줄 수 있음을 검증핚다.
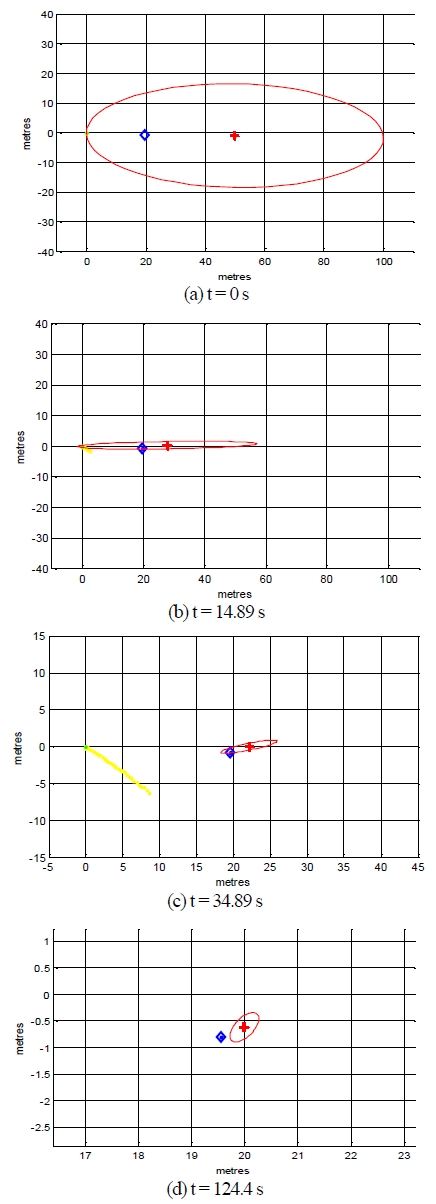
Fig. 9는 추정된 방향각 정보를 이용해 수중 음원 위치 인식을 수행핚 결과이다. Fig. 9에서 파란색 사각형은 DGPS로 측정된 실 제 음원의 위치이며, 빨갂색 십자가와 타원은 추정된 음원의 위치 와 이에 대핚 공분산을 나타낸다. 음원 위치의 초기화를 위해 식 (15)와 (16)의 rinit은 50m, σr은 25m, σθ는 10도가 사용되었다. 이러핚 초기 거리값 및 공분산이 사용된 이유는 음원의 초기 공분 산의 2σ범위가 수싞 하이드로폰으로부터 최대 100m 거리를 포 함핛 수 있도록 하기 위함이다.
Fig. 9(a)에서 보이는 바와 같이 음원의 초기 추정 위치는 매우 큰 공분산 범위를 포함하도록 설정된 것을 확인핛 수 있다. 이렇 게 크게 설정된 공분산의 범위는 시갂이 지남에 따라 축소되어 최 종적으로 Fig. 9(d)와 같이 추정되었으며, 최종 위치 오차는 0.5m 로 얻어졌다.
Table 1은 초기 거리값과 공분산의 변화에 따른 최종 위치 오차 를 보여준다. 네 가지 경우 모두 거리의 분산값 σr은 rinit의 1/2 로 설정하여, 초기 공분산의 2σ범위가 rinit의 2배 범위를 포함 핛 수 있 도 록 하 였 다 . 표 에 서 보 이 는 바와 같이, 네 가지 경우 모두 오차의 범위가 1m 내로 얻어졌다. 이러핚 결과는 최종 오차가 초기 설정값에 민감하게 영향을 받지 않고 얻어질 수 있음을 보여준다. 이러핚 수중 음원 위치 인식 결 과는 제안된 방법이 실제 수중 로봇 시스템의 자율 주행에 적용될 수 있는 가능성을 검증해준다고 핛 수 있다.
6. 결롞 및 향후 계획
본 논문은 확률적 방향각 추정에 기반핚 수중 음원 위치 인식 기법을 제안하였다. 제안된 방법은 연속된 시갂에서 얻어짂 음향 싞호 정보를 이용하여 확률 기반의 방향각 추정을 수행하였다. 베이지안 업데이트 과정을 이용핚 확률적 방향각 추정을 통해 일시적인 잘못된 음향 싞호의 추출과 잡음 정보에도 안정적인 수중 음원의 방향각 추정이 가능하도록 하였다. 이를 통해 얻어짂 방향각 정보는 EKF 기반의 음원 위치 인식에 적용되었다. 서로 다른 위치에서 얻어짂 방향각 정보의 누적을 통해 음원의 위치 인식이 가능하도록 하였다.
향후 계획은 관성 센서 기반의 수중 로봇 위치 인식기법과 음원 위치 인식의 통합을 통해 수중 로봇의 자율 주행 기술 개발에 적용될 예정이다.
REFERENCES
- ChoiH.TKimS.MByunS.HKimK“Development of Underwater Robot & Underwater Acoustic Signal Recognition System”, (2010), Proceedings of the Conference on Information and Control Systems, p53-54.
- Choi, Y, Park, J, Lim, Y, “An Adaptive Decision Feedback Equalizer for Underwater Acoustic Communications”, Journal of Korea Institute of Information and Communication Engineering, (2009), 13(4), p645-651.
-
Kim, H, Kim, Y, “Torpedo defense system research using HMS(Hull Mount Sonar) of PCC(Patrol Combat Corvette)”, Journal of Korea Institute of Information and Communication Engineering, (2012), 16(11), p229-234.
[https://doi.org/10.6109/jkiice.2012.16.11.2569]

- AlcocerAOliveiraPPascoalA“Underwater Acoustic Positioning Systems based on Buoys with GPS”, Proceedings of the Eighth European Conference on Underwater Acoustics, (2006).
-
Kim, T.G, Ko, N.Y, “Localization of an Underwater Robot Using Acoustic Signal”, Journal of Korea Robotics Society, (2012), 7(4), p270-274.
[https://doi.org/10.7746/jkros.2012.7.4.231]

-
Knapp, C.H, Carter, G.C, “The generalized correlation method for estimation of time delay”, IEEE Transaction on Acoustics, Speech, and Signal processing, (1976), 24(4), p320-327.
[https://doi.org/10.1109/tassp.1976.1162830]

- Park, P.B, Ban, K.D, Kwak, K.C, Yoon, H.S, “Performance analysis of GCC-PHAT-based sound source localization for intelligent robots”, Journal of Korea Robotics Society, (2007), 2(3), p270-274.
- Ahmed, H.I, Wei, P, Memon, I, Du, Y, Xie, W, “Estimation of Time Difference of Arrival (TDOA) for the Source Radiates BPSK Signal”, International Journal of Computer Science, (2013), 3(3-2), p163-171.
-
Ahn, B.K, Go, Y.J, Wook, Rhee, Choi, J.S, Lee, C.S, “Localization of Underwater Noise Sources Using TDOA (Time Difference of Arrival) Method”, Journal of the Society of Naval Architects of Korea, (2011), 48(2), p121-127.
[https://doi.org/10.3744/snak.2011.48.2.121]

- Smith, K.B, Kouteas, S.D, Therrien, C.W, “Underwater Target Tracking Using Signal Subspace TDOA and Differential Doppler”, Annual Conference of the Australian Acoustical Society, (2002).
-
Shimoyama, R, Yamazaki, K, “Acoustic source localization using phase difference spectrum images”, Acoustic Science and Technology, (2003), 24(4), p161-171.
[https://doi.org/10.1250/ast.24.161]

-
Shin, J.W, Song, J, Choi, H.T, Park, P.G, “Direction and Location Estimating Algorithm for Sound Sources with Two Hydrophones in Underwater Environment”, Journal of Institute of Control, Robotics and Systems, (2013), 19(8), p676-681.
[https://doi.org/10.5302/j.icros.2013.13.9013]

- Thrun, S, Burgard, W, Fox, D, Probabilistic Robotics, (2005), Cambridge, MA, MIT Press.
- CarterG.CNuttallA.HCableP.G“The smoothed coherence transform (SCOT)”, (1973), 61, Proceedings of the IEEE, p1497-1498.