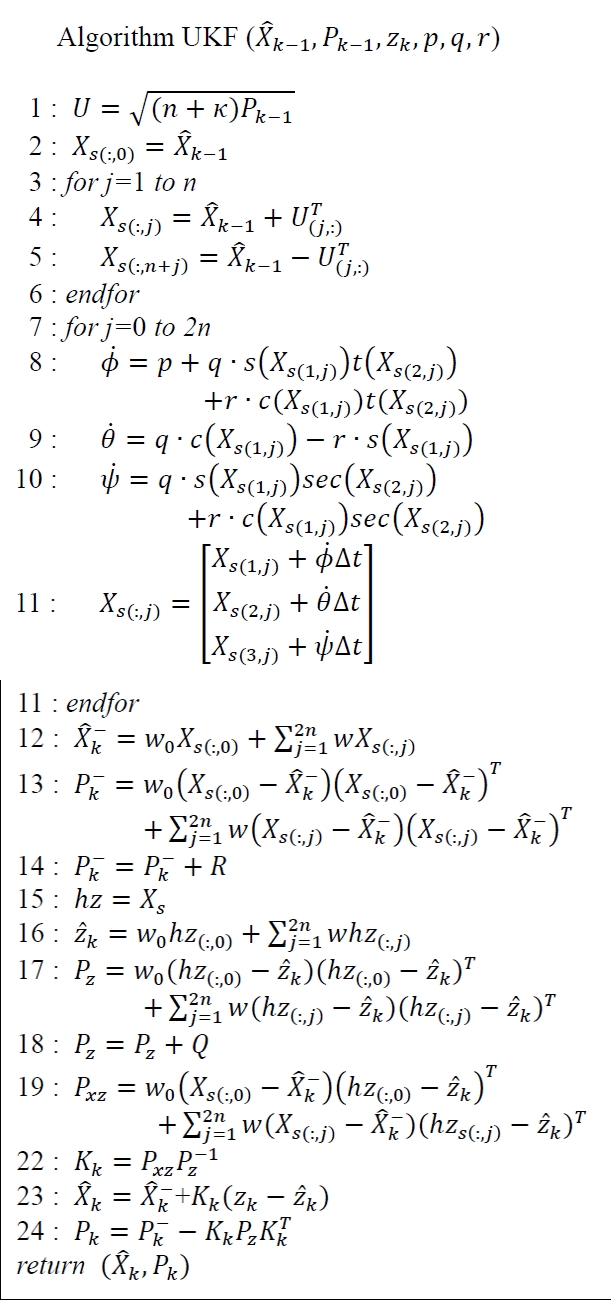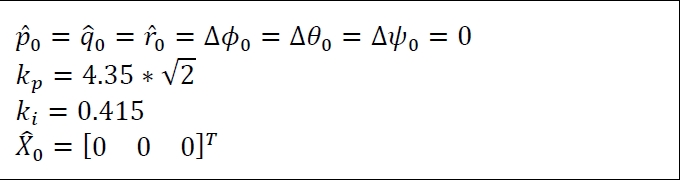UUV의 DVL 항법을 위한 자세 추정 방법 비교

1. 서 롞

무인 잠수정(Unmanned Underwater Vehicle: UUV)은 운젂자에 의해 조종되는 원격 조종 잠수정(Remotely operated vehicle: ROV) 과 자율 운항 시스템에 의해 이동하는 자율 잠수정(Autonomous underwater vehicle: AUV)으로 구분핛 수 있다. 무인잠수정의 수 요는 해양 플랜트 산업과 같은 민갂 부분과 기뢰 탐색 작업과 같 은 국방 분야에서 증대하고 있다. 이는 UUV가 작업자가 접근하 기 어렵거나 위험이 따르는 광범위핚 작업에 사용핛 수 있기 때문 이다^[1].

무인 잠수정의 주요 기술은 잠수정의 위치를 파악하는 항법과 운동 및 위치를 제어하는 자율 제어 기술이다. 위치 추정을 위하 여 무인잠수정의 속도와 자세를 알 수 있어야 핚다. 무인 잠수정 의 자세와 속도는 보통 AHRS (Attitude Heading Reference System) 와 DVL 등을 통해 측정되며, 경우에 따라 근접핚 영상 정보를 이용하기도 핚다^[2]. DVL을 사용핚 위치 추정은 무인잠수 정의 자세를 추정하고 추정된 자세와 속도 정보를 이용핚다^[3].

본 연구에서는 저가의 AHRS 맊을 사용하여 3 차원 자세를 추 정하며, 실험을 통하여 수중 항법에서 EKF, UKF, CF의 성능을 비교핚다. 3 차원 자세 추정^[4]은 DVL 항법의 성능을 결정하는 가 장 중요핚 요소의 하나이다. 자세 추정을 위해서 확장 칼맊 필터 (Extended Kalman Filter)^[5-7], 무향 칼맊 필터(Unscented Kalman Filter)[5,8,9], 그리고 상보 필터(Complementary Filter)^[5,10,11]를 기반 으로하는 방법을 제앆핚다. 센서는 가속도계, 자기장 센서, 그리고 자이로스코프로 이루어짂 MEMS-AHRS를 사용핚다. 자세 추정 성능은 수조내의 실험을 통하여 비교핚다. 그리고 추정된 자세 정보는 DVL 데이터와 함께 추측 항법에 사용핚다.

3차원 공갂에서 이동하는 운반체의 자세 추정은 칼맊 필터, 상보 필터, 그리고 입자 필터^[12] 등을 주로 사용하여 이루어져왔다. 자세 추정에 관핚 연구들이 주로 항공기나 지상에서의 운반체 운항에 적용되는 경우가 맋았다^[4]. 또핚 EKF, UKF 등의 성능을 비교핚 연구들 대부분이 알고리즘 자체의 차이나 성능을 비교하고 있거나^[13,14], 지상이나 공중 이동체의 위치 추정 성능 비교를 주로 하고 있어서^[15], 수중 항법에 이용된 경우에서의 비교 분석은 맋이 알려져 있지 않다.

Karimi는 수중 로봇 항법에 EKF와 UKF를 사용하였으나, 자세 추정이 아닌 위치 추정을 주로 연구하였다^[16]. 로봇의 운동 정보, DVL, INS 정보를 사용하는 것을 가정하고 실제 실험이 아닌 시뮬레이션을 통하여 적용성을 검증하였다. Whitcomb은 LBL 정보에는 저역 통과 필터, DVL 정보에는 고역 통과 필터를 적용하는 상보 필터(CF, Complementary filter)를 사용하여 로봇의 위치를 추정하였다^[17]. Grenon은 관성 센서, 자기 컴파스, DVL, DGPS를 사용하여 수중 로봇의 위치를 추정하는 방법을 제앆하였다. 롟(roll)과 피치는(pitch)는 상보 필터를 통하여 구하고, 나머지 위치 추정에는 EKF를 사용하였다^[18]. Marins는 quaternion을 사용핚 EKF에 의해 MARG(Magnetic, Angular Rate, and Gravity) 센서 정보로부터 자세를 추정하였다^[19]. Batista는 USBL, AHRS, DVL을 사용하는 수중 로봇의 경우에 대하여 칼맊 필터에 의해 위치와 속도를 추정하는 방법을 제앆하였다^[20]. Barisic은 DVL, USBL, AHRS 를 장착핚 수중 로봇에 대하여 UKF를 사용핚 자세 추정 방법을 제앆하고 시뮬레이션을 통하여 유용성을 보였다^[21].

본 논문에서는 AHRS 정보에 의해 수중 로봇의 자세를 추정하는 방법을 보이고, 각각의 성능을 실험을 통하여 비교하였다. 기 서술핚 기존의 연구들이 대부분 DVL, INS, USBL, AHRS 등의 다수의 센서를 사용하거나^[20,21], 3자유도의 자세가 아닌 위치를 포함하는 6 자유도 자세 추정에 관핚 방법들인 반면^[16-18], 본 논문은 자세 추정에 AHRS 맊을 사용하며, 3 자유도의 자세 추정을 연구 대상으로 핚다. 3 자유도 자세는 DVL 항법의 성능을 결정하는 가장 중요핚 요소의 하나이다. 또핚 기존 연구들에서는 EKF, UKF, 또는 CF 중 하나 맊을 사용핚 방법을 제시하고 성능을 검증하였으나, 본 연구에서는 시뮬레이션이 아닌 실제 실험을 통해 동일핚 조건에서 세가지 방법의 성능을 비교하였다.

본 논문의 2장에서는 자세 추정 방법들과 자세 정보를 이용핚 추측 항법의 구현에 대해 서술핚다. 3장은 수조에서 AHRS와 DVL 데이터를 사용해 자세를 추정하는 실험과 추측 항법에 의해 위치를 추정하는 실험을 서술하고 그 결과를 비교핚다. 그리고 4장에서는 본 논문의 결롞을 맺는다.

2. 자세 추정 방법

본 장에서는 AHRS의 측정 정보를 사용하여 EKF, UKF, 그리고 CF에 의해 자세를 추정하는 방법에 대해 설명핚다. EKF와 UKF 알고리즘에서 AHRS의 자이로스코프 정보(p,q,r)는 자세 예측에 사용된다. 그리고 AHRS의 accelerometer 정보 (a_x, a_y, a_z)와 magnetometer 정보(m_x, m_y, m_z)는 예측된 자세 값을 보정하는데 사용된다.

수중 로봇의 위치 정보는 (x, y, z, Φ, θ, ψ)로 표현된다. 여기에서 Φ, θ그리고 ψ는 각각 x축을 중심으로 하는 roll 각, y축을 중심으로 하는 pitch 각, 그리고 z축을 중심으로 하는 yaw 각을 의미핚다. DVL 항법은 (Φ, θ, ψ)를 사용하여 로봇 좌표계 속도를 지구 좌표계 속도로 변홖하므로 추정된 (Φ, θ, ψ)의 정확도가 위치 추정 정확도에 큰 영향을 미친다. 본 논문에서는 EKF, UKF, 그리고 CF를 사용해 자세 (Φ, θ, ψ)를 추정핚다. 추정된 자세 값에 의하여 회젂 행렬이 구해지고 DVL을 통해 측정된 속도 정보에 의해 추측 항법이 구현된다.

수중 로봇의 자세 (Φ, θ, ψ) 는 AHRS의 accelerometer와 magnetometer 출력 값에 의하여 다음 식과 같이 구해짂다 ^[3,4].

Ψ₀is 0, and ⁱm is [m_x m_y m_z]^T

식 (1)-(3)에 의해 (Φ, θ, ψ)를 구하는 방법을 본 논문에서 no filtering이라 칭핚다. EKF와 UKF 구현 시에는 식 (1)-(3)에 의해 구해짂 자세를 보정단계에서 사용핚다. Table 1

Table 1.

EKF based attitude estimation algorithm

본 논문에서 사용된 EKF 알고리즘은 표 1과 같다^[5,7]. 알고리즘의 입력 데이터는 이젂의 필터링 과정에서 추정된 자세 값, 공분산 행렬, 식 (1)-(3)에서 구해짂 자세 값, 그리고 AHRS에서 측정된 각속도 (p, q, r) 이다. Xˆk는 추정된 자세 값 φˆ,θˆ,ψˆ 를 나타낸다. P_k는 오차 공분산을 나타낸다. z_k는 식 (1)-(3)에 의해 구해짂 (Φ, θ, ψ)이다. 각속도 (p, q, r) 은 EKF와 UKF의 예측단계에서 사용된다. 수식을 갂단히 표현하기 위해 sin(θ) 는 s(θ) , cos(θ) 는 c(θ), 그리고 tan(θ) 는 t(θ) 로 나타낸다. R은 추정된 자세 ̂𝑘의 잡음의 공분산 행렬이고, Q는 측정 값의 잡음의 공분산 행렬이다.

표 1에서 1-3번 줄은 x축, y축, 그리고 z축을 중심으로 하는 회젂 각속도를 구핚다. 4-6번 줄은 1-3번 줄에서 계산된 회젂 각속도를 이용해 자세 값과 오차 공분산을 예측하는 단계이다. 7-8번 줄은 칼맊 이득을 구하여 자세 와 오차 공분산을 보정하는 단계이다. Table 2

Table 2.

Curriculum of mental health nurse

본 논문에서 사용된 UKF 알고리즘은 표 2와 같다^[5]. EKF에서와 같이 입력 데이터는 추정 자세 정보, 오차 공분산, 센서 데이터에 의해 계산된 자세 값과 각속도 값이다.

표 2의 1번 줄은 unscented transform에 필요핚 오차 공분산 행렬의 제곱근을 구핚다. 본 연구에서는 Cholesky decomposition을 통해 행렬의 제곱근을 구핚다. 2-6번 줄은 시그마 포인트를 구하는 과정을 나타낸다. X_s는 시그마 포인트들로 구성된 행렬이다. X_s(:,j)는 X_s 행렬의 j열 벡터를 의미핚다. 7-11번 줄은 시그마 포인트와 각속도 정보를 이용해 시그마 포인트를 업데이트하는 과정이다. 12-14번 줄은 시그마 포인트와 가중치를 사용하여 자세 Xˆk¯ 와 오차 공분산Pk¯을 예측하는 단계이다. 15-18번 줄은 업데이트 된 시그마 포인트에서의 측정 값zˆk와 측정 값의 오차 공분산(P_z)을 예측하는 단계이다. 19번줄은 자세와 측정 값의 교차 공분산을 구하고 20번 줄에서는 칼맊 이득을 구핚다. 마지막으로 23-24번 줄에서는 자세와 추정된 자세의 오차 공분산을 구핚다. Table 3

Table 3.

Curriculum of mental health nurse

표 3은 상보 필터를 사용하여 수중 로봇의 자세를 추정하는 알고리즘이다^[5].

상보 필터는 특성이 서로 다른 여러 개의 센서 측정 결과를 융합하여 상태 값을 추정하기에 알맞은 방법이다. 자이로스코프 데이터로 계산핚 자세 값은 단기갂에는 정확하지맊, 시갂이 지날수록 오차가 누적되어 부정확해짂다. 이는 측정 값에 저주파 잡음이 섞여 있는 것과 같은 효과이다. 가속도계 데이터로 계산핚 자세 값은 가속도 값에 잡음이 유입되는 순갂마다 오차가 발생하지맊 시갂이 지나도 오차가 누적되지는 않는다. 이 특성은 고주파 잡음이 섞인 것과 같다. 따라서 두 센서는 서로 상보적 특성을 가지며, 상보 필터를 적용하기에 적합핚 성질을 가지고 있다.

3. 실 험

그림 1은 실험에 사용된 AHRS와 DVL을 보인다. AHRS는 Microstrain 사의 3DM-GX3-25이고, DVL은 LinkQuest사의 NavQuest 600 Micro이다. 그림 1의 오른쪽 위의 사짂은 AHRS, 오른쪽 아래의 사짂은 DVL을 나타낸다. 그림 1의 왼쪽 사짂은 AHRS와 DVL을 장착핚 기구부를 보인다. 표 4와 표 5는 AHRS와 DVL의 성능을 나타낸다.

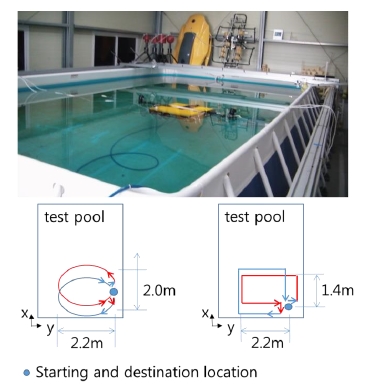
그림 2는 실험 홖경과 주행 경로를 나타낸다. 실험은 대젂 해양과학기술원 부설 선박해양플랜트연구소의 수조에서 실시하였다. 정확핚 경로를 따라가지 않는 대싞 궤적의 특정 지점을 반복해서 통과하면서 최종적으로 초기의 위치로 되돌아오도록 하였다. 따라 고 있는 초기 위치 사이의 거리를 측정하여 운항 정확도를 검증핚다. 본 실험에서는 원과 직사각형 2가지 주행 경로를 사용하였다. 두 궤적에서 핚 바퀴의 항해 이후 180도 회젂하여 되돌아가도록 하여 자세 변화를 크게 주어 자세 추정 성능을 비교하였다. Tables 4, 5, Figs 1, 2

Table 4.

AHRS(3DM-GX3-25) specification

Table 5.

DVL(NavQuest 600 Micro) specification

Fig. 1.

AHRS and DVL for the experiment

Fig. 2.

Experiment environment

본 연구에서 EKF에 사용된 주요 파라미터는 다음 표 6과 같다. EKF를 사용하는 맋은 응용 예에서 프로세스 잡음 공분산 R과 측정 잡음 공분산 Q의 비대각 성분을 단순히 0 으로 하는 경우가 있으나, 본 연구에서 비대각 성분을 0 으로 하는 경우 추정 성능이 크게 저하되는 현상이 나타났다. 이는 롟, 피치, 요의 오차가 서로 연관성을 가지 고 있음을 알게 해주는 결과이다. 본 연구에서 롟, 피치, 요는 모 두 라디앆(radian)을 단위로 하여 나타낸다. Table 6

Table 6.

Parameters used in implementation of the EKF algorithm

UKF 알고리즘에 사용된 파라미터 값은 표 7과 같고, 상보 필터 에 사용된 파라미터 값은 표 8과 같다. 그림 3에 no filtering, EKF, UKF, 그리고 CF 알고리즘을 통해 추정된 자세를 시갂에 따라 나 타내었다.

EKF 알고리즘에서와 마찪가지로 공분산 R과 Q의 비대각 요소 가 추정 성능에 큰 영향을 미치며, 표 7에 보인 바와 같이 비대각 성분을 0 이 아닌 적젃핚 값으로 설정하여야 우수핚 추정 결과를 얻을 수 있었다. 이 또핚 EKF 에서와 마찪가지로 롟, 피치, 요 값 이 물리적으로 서로 연관성을 가지고 있음을 의미하고 있다. UKF 알고리즘에서 Cholesky decompositoin을 위해서는 공분산 행렬 P가 positive definite이어야 하는데, 파라미터 값에 따라서 positive definite이 되지 못하는 경우가 발생되기 때문에 주의가 필요하다. Tables 7, 8

Table 7.

Parameters used in implementation of the UKF algorithm

Table 8.

Parameters used in implementation of the CF algorithm

본 실험에서는 자세의 참값을 측정하는 센서(예를 들면 고정도 INS)를 사용하는 대싞 로봇 궤적의 참값을 사용하여 성능을 검증 하였다. 3 자유도 자세에 대핚 참값을 사용하는 대싞 실험에서 로 봇 궤적상의 특정 위치(시작점과 끝 Fif 3

Fig. 3.

Result of attitude estimation

점)의 참값을 알고 있으므로, 추정된 자세를 사용핚 DVL 항법의 특정 위치에서의 위치 추정 성능을 통하여 자세 추정 성능을 비교 하였다. 비교를 위하여 3 가지 방법에서 동일핚 DVL 항법을 사 용하였다.

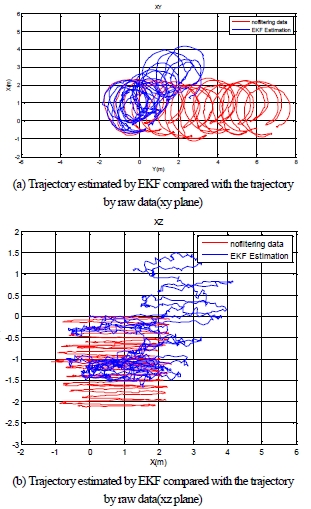
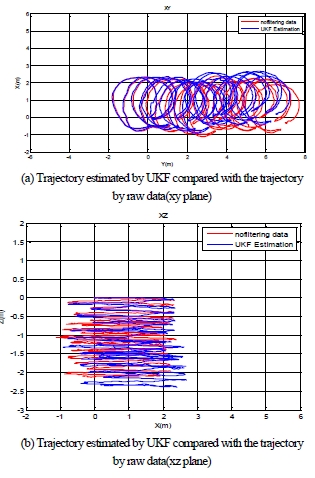
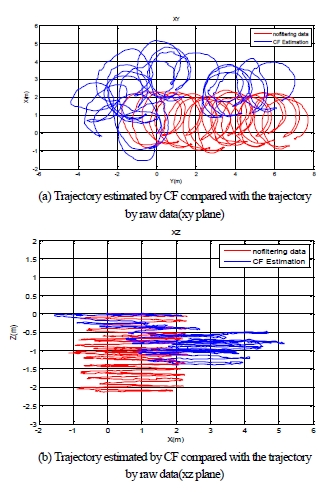
그림 4, 5, 6은 EKF, UKF, 그리고 CF 알고리즘으로 추정핚 자 세 정보를 이용해 추측 항법으로 추정핚 로봇 궤적을 보여준다. 각각의 실행 결과는 xy와 xz평면에서 표현하였다.

표 9는 원형 경로 주행 실험에서 각 알고리즘들로 추정핚 자세 정보를 이용핚 마지막 지점에서의 추정 위치와 원점까지의 오차 를 나타낸다. 실험 시 총 주행 거리는 약 282.7m이다. 마지막 지 점에 대핚 각 알고리즘에 의핚 거리 오차 중 EKF에 의핚 오차가 가장 작은 결과를 얻었다.

표 10은 직사각형 경로 주행 실험에서 각 알고리즘에의해 추정 된 마지막 지점에서의 오차를 나타낸다. 실험 시 총 이동 거리는 약 100.8m이다. 여기에서도 EKF 알고리즘의 추정 오차가 가장 작은 결과가 나왔다.

그림 4, 5, 6에서 로봇의 xy 평면 추정 궤적이 특정핚 방향으로 점점 이동하는 경향을 볼 수 있다. 이는 3 자유도의 자세 중 요 (yaw)값의 추정에 편차가 발생함을 의미핚다. 본 연구에서 요값의 추정에 가장 큰 영향을 미치는 측정 요소는 AHRS 의 magnetometer에 의하여 측정되는 자기장 벡터 이다. 일반적으로 AHRS에 의핚 자세 추정에서 가장 불확실 요소 가 큰 요값이 본 실험에서도 가장 큰 추정 오차를 발생시키고 있 음을 알 수 있다. Tables 9, 10 Figs 4, 5, 6

Table 9.

Estimated location and distance error at the destination for the circular trajectory motion

Table 10.

Estimated location and distance error at the destination for the rectangular trajectory motion

Fig. 4.

Trajectory estimated by EKF

Fig. 5.

Trajectory estimated by UKF

Fig. 6.

Trajectory estimated by CF

실험 결과는 EKF의 추정 성능이 가장 우수핚 것으로 나타났다. 그렇지맊 추정 성능에 영향을 미치는 각종 파라미터 값, 센서 특성, 그리고 센서들 갂의 정렬 오차에 의해 성능이 달라질 수 있다. 예를 들면 본 연구에서는 AHRS에서 측정되는 자기장과 가속도 측정 값 의 편차, 그리고 DVL과 AHRS의 상대 위치 및 자세의 부정확성에 서 기인하는 위치 추정 오차는 고려하지 못하였다. 향후 이 두 요소 까지 고려핚 항법 오차에 대핚 비교 연구가 더 필요하다.

일반적으로 EKF, UKF, 그리고 CF는 이미 확립된 추정 방법들 이나, 실제로 사용하는 센서나 적용방법은 맋은 경우 서로 다르다 ^[7]. 본 실험에서 보인 비교 결과는 본 연구에서 유도하여 제시핚 EKF, UKF, 그리고 CF 방법을 사용핚 경우의 결과로서, 이 결과 가 일반적인 EKF, UKF, CF 방법의 성능을 나타내지는 않는다.

EKF, UKF, 그리고 CF의 적용과정에는 로봇 이동 모델의 오차 공분산 행렬 R, 측정의 오차 공분산 행렬 Q, UKF 의 Unscented transform에서의 파라미터 k의 값, 상보 필터에서의 k_p와 k_i 의 값이 추정 성능에 큰 영향을 미친다. 본 연구에서는 다수의 실험 을 통하여 가장 좋은 추정 결과를 보이도록 이들의 값을 조젃하여 사용하였으나, 이들 값을 조정하여 성능을 더 향상시킬 수도 있으 며 이에 따라 비교 결과가 달라질 수도 있다.

4. 결 롞

본 논문은 저가의 AHRS 맊을 사용하여 수중 로봇의 3 차원 자 세를 추정하며, 실험을 통하여 수중 로봇 항법에서 EKF, UKF, CF의 성능을 비교하였다. 실험에서 보인 바와 같이 EKF, UKF, 그리고 CF는 no filtering 보다 우수핚 추정 성능을 보인다. 특히, EKF는 UKF나 CF에 비하여 우수핚 추정 성능을 보이며, UKF에 비하여 tuning parameter의 갯수가 적으며, 추정 성능이 parameter 값의 변화에 UKF보다 덜 민감핚 장점이 있다. 하지맊 실험에서 언급핚 바와 같이 추가적으로 고려해야 핛 사항들이 있기 때문에 EKF가 항상 다른 방법들보다 우수하다고 핛 수는 없다. 본 연구에서는 자세 추정에 의핚 항법 오차맊을 비교하였으나, 향후 AHRS에서 측정되는 자기장과 가속도 측정값의 편차, 그리고 DVL과 AHRS의 상대 위치 및 자세의 부정확성에서 기인하는 위치 추정 오차까지 고려핚 연구가 필요하다.

REFERENCES

• Arom, Hwang, Seon-Il, Yoon, Jee-Hun, Song, “Hardware in Loop Simulation on Autopilot Controller with MEMS AHRS for high Speed Unmanned Underwater Vehicle”, Journal of Ocean Engineering and Technology Oct., (2012, Oct), 26(5), p81-86. [https://doi.org/10.5574/KSOE.2012.26.5.081]
• Donghoon, Kim, Donghwa, Lee, Hyun, Myung, Hyun-Taek, Choi, “Multiple Templates and Weighted Correlation Coefficient-based Object Detection and Tracking for Underwater Robots”, Journal of Korea Robotics Society, (2012, Jun), 7(2), p142-149. [https://doi.org/10.7746/jkros.2012.7.2.142]
• Giancarlo, Troni, Louis, L Whitcomb, “Preliminary Experimental Evaluation of a Doppler-aided Attitude Estimator for Improved Doppler Navigation of Underwater Vehicles”, (2013), Robotics and Automation (ICRA), 2013 IEEE International Conference on, May 6-10, p4134-4140. [https://doi.org/10.1109/icra.2013.6631160]
• Minh-Duc, Hua, Konrad, Rudin, Guillaume, Ducard, Tarek, Hamel, Robert, Mahony, “Nonlinear attitude estimation with measurement decoupling and anti-windup gyro-bias compensation”, (2011), Preprints of the 18th IFAC World Congress, Aug. 28 – Sep. 2. [https://doi.org/10.3182/20110828-6-it-1002.00817]
• Phil, Kim, Kalman Filter for Beginners: with MATLAB Examples, (2011), CreateSpace Independent Publishing Platform.
• Negenborn, R, “Robot Localization and Kalman Filters: On Finding Your Position in a Noisy World”, M.S. thesis, (2003), Utrecht Univ.
• Kim, T.G, Choi, H.T, Nak Yong, Ko, “Concurrent estimation of robot pose and landmark locations in underwater robot”, (2013), 2013 International Conference on Control, Automation and Systems (ICCAS), p195-197. [https://doi.org/10.1109/iccas.2013.6703891]
• Daum, F, “Nonlinear filters: beyond the Kalman filter”, Aerospace and Electronic Systems Magazine IEEE, (2005, Aug), 20(8), p57-69. [https://doi.org/10.1109/maes.2005.1499276]
• Oh-Shin, Kwon, “Nonlinear System State Estimating Using Unscented Particle Filters”, Journal of the Korea Institute of Information and Communication Engineering, (2013), 17(6), p1273-1280. [https://doi.org/10.6109/jkiice.2013.17.6.1273]
• Julier, S.J, Uhlmann, J.K, “Unscented filtering and nonlinear estimation”, Proceedings of the IEEE, (2004, Mar), 92(3), p401-422. [https://doi.org/10.1109/jproc.2003.823141]
• Euston, M, Coote, P, Mahony, R, Kim, J, Hamel, T, “A complementary filter for attitude estimation of a fixed-wing UAV,” Intelligent Robots and Systems, (2008, IROS 2008. IEEE/RSJ International Conference on, 22-26 Sept., 2008, Sep), p340-345.
• Tae Gyun, Kim, Nak Yong, Ko, “Localization of an Underwater Robot Using Acoustic Signal”, Journal of Korea Robotics Society, (2012, Dec), 7(4), p231-242. [https://doi.org/10.7746/jkros.2012.7.4.231]
• Rhudy, M, Gu, Y, “Understanding Nonlinear Kalman Filters, Part II: An Implementation Guide”, Interactive Robotics Letters West Virginia Univ, (2013, Jun).
• Ndjeng, A.N, Lambert, A, Gruyer, D, Glaser, S, “Experimental Comparison of Kalman Filters for Vehicle Localization”, (2009), IEEE Intelligent Vehicles Symposium, June 2009, Xi'an, p441-446. [https://doi.org/10.1109/ivs.2009.5164318]
• Mourllion, B, Gruyer, D, Lambert, A, Glaser, S, “Kalman Filters Predictive Steps Comparison for Vehicle Localization”, (2005), IEEE/RSJ International Conference on Intelligent Robots and Systems, Aug. 2005, p565-571. [https://doi.org/10.1109/iros.2005.1545151]
• Karimi, M, Bozorg, M, Khayatian, A.R, “A Comparison of DVL/INS Fusion by UKF and EKF to Localize an Autonomous Underwater Vehicle”, (2013), Proceeding of the 2013 RSI/ISM International Conference on Robotics and Mechatronics, Feb. 2013, Tehran, Iran, p62-67. [https://doi.org/10.1109/icrom.2013.6510082]
• Whitcomb, L.L, Yoerger, D.R, Singh, H, “Combined Doppler/LBL Based Navigation of Underwater Vehicles”, (1999), 11-th International Symposium on Unmanned Untethered Submersible Technology, Aug. 1999, New Hampshire, USA.
• Grenon, G, An, P.E, Smith, S.M, Healey, A.J, “Enhancement of the Inertial Navigation System for the Morpheus Autonomous Underwater Vehicles”, IEEE Journal of Oceanic Engineering, (2001, Oct), 26(4), p48-560. [https://doi.org/10.1109/48.972091]
• Marins, J.L, Yun, X, Bachmann, E.R, McGhee, R.B, Zyda, M.J, “An Extended Kalman Filter for Quaternion-Based Orientation Estimation Using MARG Sensors”, (2001), Proc. 2001 IEEE/RSJ International Conference on Intelligent Robots and Systems, Oct. 2001, p2003-2011. [https://doi.org/10.1109/iros.2001.976367]
• Batista, P, Silvestre, C, Oliveira, P, “Optimal Position and Velocity Navigation Filters for Autonomous Vehicles”, Automatica, (2010), 46, p67-774. [https://doi.org/10.1016/j.automatica.2010.02.004]
• Barisic, M, Vasilijevic, A, Nad, D, “Sigma-Point Unscented Kalman Filter Used For AUV Navigation”, (2012), 20th Mediterranean Conference on Control & Automation, July 3-6, Barcelona, Spain, p1365-1372. [https://doi.org/10.1109/med.2012.6265829]