차륜형 이동로봇의 오도메트리 보정을 위한 실험적 주행시험경로 설계
†Corresponding author: Mechanical Engineering, Korea University, Anam-Ro, Seongbuk-Gu, Seoul, Korea ( smartrobot@korea.ac.kr)
© KROS
Abstract
Odometry using wheel encoder is a common relative positioning technique for wheeled mobile robots. The major drawback of odometry is that the kinematic modeling errors are accumulated when the travel distance increases. Therefore, accurate calibration of odometry is required. In several related works, various schemes for odometry calibration are proposed. However, design guidelines of test tracks for odometry calibration were not considered. More accurate odometry calibration results can be achieved by using appropriate test track because the position and orientation errors after the test are affected by the test track. In this paper, we propose the design guidelines of test tracks for odometry calibration schemes using experimental heading errors. Numerical simulations and experiments clearly demonstrate that the proposed design guidelines result in more accurate calibration results
Keywords:
Calibration, Localization, Mobile robots, Odometry, Systematic error1. 서 론
최근 이동로봇의 자율주행과 관련하여 다양한 연구가 진행되고 있다[1-2]. 이동로봇의 자율주행을 위해 필요한 기 술 중 한 가지는 정밀한 위치인식이다. 로봇 위치인식에 사용되는 일반적인 방법의 하나는 로봇의 구동부에 내장 된 휠 엔코더를 이용하는 오도메트리이다. 그러나 오도메 트리는 주행거리가 증가함에 따라 오도메트리 상의 로봇 위치와 실제 로봇 위치 간의 오차가 증가한다는 잘 알려 진 단점을 가지고 있다. 따라서 주행거리에 따라 증가하는 오차를 감소시키기 위해 오도메트리 보정이 필요하다. 정 밀한 오도메트리는 외장센서의 설치, 보수 등에 관련된 운 용비용을 감소시킬 수 있다. 또한, 날씨나 주행환경 등 주 행조건에 인해 외장 센서의 사용이 제한될 경우에도 비교 적 정밀한 위치인식이 가능하게 한다.
오도메트리의 오차 원인은 크게 시스템적 오차와 비시 스템적 오차 두 가지로 구분된다[3-6]. 시스템적 오차는 로봇 자체에서 기인하는 고유한 오차로, 주행하는 동안 변하지 않는다. 따라서 기구학적 파라미터를 보정함으로써 시스템 적 오차를 감소시킬 수 있다. 대표적인 시스템적 오차는 좌우 휠 직경 차이와 좌우 휠 간격 오차이다.
비시스템적 오차는 로봇과 주행환경 사이의 상호작용에 기인하는 오차이다. 불균일한 바닥, 바닥 장애물, 급격한 가-감속, 외력 등에 의한 미끄러짐이 비시스템적 오차에 포함된다. 비시스템적 오차는 항상 일정하게 발생하는 것 이 아니라 확률적으로 발생하는 오차이다. 따라서 Thrun의 오도메트리 모델[6]과 같이 오도메트리를 확률 모델로 표현 하기도 한다.
기존의 여러 연구에서 다양한 오도메트리의 시스템적 오차 보정기법이 제안되었다. Borenstein[4]은 이륜차동구동 형 로봇의 오도메트리 보정에 유용한 기법인 UMBmark 기법을 제안하였다. UMBmark 기법은 4m×4m 정사각형 경로를 시계 및 반시계방향으로 주행하고 최종 위치 오차 를 측정하여 휠 직경 오차와 휠 간격 오차를 보정한다. Abbas[7]는 정사각형 경로가 아니라 원형 경로를 시계 및 반시계방향으로 주행하고, 주행 경로의 반경을 측정하여 오차를 보정하는 BCPT(Bi-directional Circular Path Test)를 제 안하였다. Martinelli[8]는 싱크로구동형 로봇의 오도메트리 오차를 시스템적 오차 및 비시스템적 오차를 나타내는 4 개의 파라미터(병진 및 회전)로 모델링하고 평가하는 방법 을 제안하였다. Martinelli[9]는 AKF(augmented Kalman filter)와 OF(Observable filter)를 기반으로 로봇이 주행하는 동안 오 도메트리 오차를 추정하는 방법을 제안하였다. Antonelli[10] 는 최소자승법을 이용한 오도메트리 보정기법을 제안하였 다. 오도메트리는 4개의 파라미터를 이용하여 모델링 되었 으며, 미지의 파라미터와 센서 측정값 간의 선형관계를 보 임으로써 최소자승법이 오도메트리 보정이 유효하게 사용 될 수 있음을 보였다. 이후 Antonelli[11]는 추가적인 연구를 통해 오도메트리 모델을 3개의 파라미터로 모델링하고 보 정하는 기법을 제안하였다. 최근에는 Censi[12], Antonelli[13]가 오도메트리와 로봇프레임에 대한 센서의 위치를 동시에 보정하는 기법을 제안하였다.
비시스템적 오차와 관련해서는 Borenstein[14]과 Komoriya[15] 와 같이 오도메트리와 자이로 센서를 함께 사용함으로써 비시스템적 오차에 대응하고 위치인식의 불확실성을 감소 시키는 방법이 제안되기도 하였다. Chong[16]은 로봇의 주행 경로를 원호로 나누고 오차 공분산 행렬을 표현하는 방법 을 제안하였다. 오차 공분산 행렬을 계산하기 데 필요한 운동 불확실성에 대한 파라미터, 즉 비시스템적 오차 파라 미터를 10m 직선 경로를 왕복 주행한 결과로부터 계산하 는 실험방법 또한 함께 제안하였다.
이전의 연구에서는 이륜차동구동형로봇에 대해 오차원 인간의 복합효과를 고려한 정밀한 오도메트리 보정기법[17] 을 제안하고 적절한 주행시험경로 설계를 통한 보정성능 향상[18]을 보였다. 또한, 최종 방향각 오차를 이용하는 새로 운 오도메트리 보정기법[19]을 제안하였다. 새로운 보정기법 은 최종 위치 오차가 아닌 최종 방향각 오차를 보정과정 에 이용함으로써 근사식 사용에 의한 오차를 제거하여 보 정성능을 향상시켰다. 또한, 자이로 센서만으로도 오차 보 정이 가능하여 시험환경에 별도의 절대 위치센서를 설치 할 필요가 없으며, 실외에서도 보정실험이 가능하였다.
이전 연구의 과정 및 결과에서 주행시험경로 설계가 오 도메트리 보정성능의 영향을 미치는 중요한 요소임을 확 인하였다. 그러나 기존 문헌에서는 주행시험경로 설계에 대한 내용은 중요하게 다루어지지 않았다.
본 논문에서는 오도메트리 보정성능 향상을 위한 주행 시험경로 설계기법에 대해 다루고자 한다. 주행시험경로는 여러 가지 오도메트리 오차 원인의 영향을 주행시험 후 나타나는 최종 위치 및 방향각 오차에 투영할 수 있어야 하며, 보정기법의 특성을 고려하여 설계되어야 한다. 적절 한 주행시험경로를 사용함으로써 오도메트리 보정 정밀도 의 향상을 기대할 수 있다.
본 논문은 다음과 같이 구성된다. 2장에서는 오도메트리 오차 모델에 대해서 다룬다. 3장에서는 주행시험경로 설계 간 고려사항을 언급하고 주행시험경로 설계기법을 제안한 다. 4장과 5장에서는 시뮬레이션과 실험 결과를 통해 제안 하는 설계기법의 장점을 확인한다.
2. 오도메트리 오차 모델
2.1. 시스템적 오차
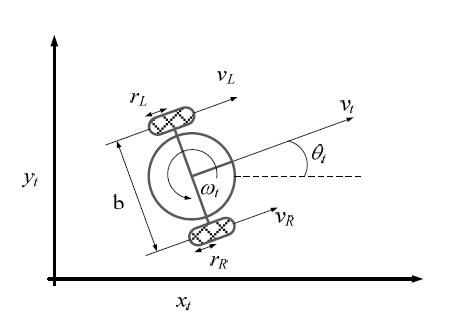
Fig. 1은 이륜차동구동형로봇의 속도운동모델을 나타낸 다. 시간 t에서의 로봇의 위치 및 방향각은 (xt, yt, θt)와 같다. 시간 t에서의 병진속도 및 회전속도는 각각 vt와 ωt이다. 시 스템적 오차에 있어 주된 오차 원인 두 가지는 휠 직경 오 차와 휠 간격 오차이다. 좌우 휠에 각각 εrR, εrL만큼의 반경 오차가 있고, 휠 간격에 εb만큼의 오차가 있다고 할 때, 이 륜차동구동형로봇의 속도운동모델은 다음의 식 (1) – (2)와 같이 표현된다.
| (1) |
| (2) |
이때, vR은 우측 휠의 선속도를, vL은 좌측 휠의 선속도를, ωR 은 우측 휠의 각속도를, ωL은 좌측 휠의 각속도를 각각 나타낸다.
식 (1) – (2)를 이용하여 전역좌표계에서 x, y, θ는 다음 식 (3)과 같이 표현된다.
| (3) |
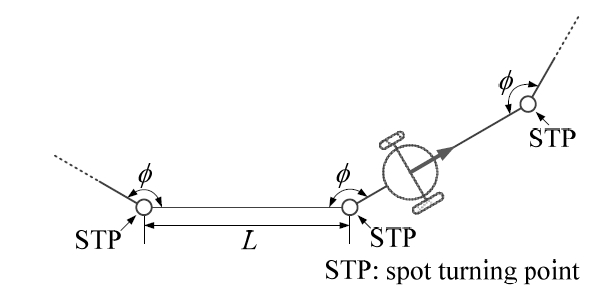
오도메트리의 시스템적 오차는 기 정의된 주행시험경로 를 오픈-루프 제어로 주행한 후 최종 포즈(위치 및 방향각) 오차를 측정함으로써 보정된다. 주행시험경로는 휠 직경 오차의 영향과 휠 간격 오차의 영향을 모두 포함하기 위 하여 직선주행과 제자리회전을 포함하며, 오차측정을 용이 하게 하기 위해 출발점과 도착점을 동일하게 설정한다. 위 조건을 만족하는 주행시험경로는 Fig. 2와 같이 정다각형으 로 일반화될 수 있다. Fig. 2에서 L은 직선 경로의 길이를, φ 는 이웃한 직선 경로 사이의 각도를 나타낸다.
Fig. 2와 같은 주행시험경로를 주행한 후, 기구학적 오차 εrR, εrL, εb에 의해 발생한 최종 포즈오차(xe, ye, θe)는 식 (3)을 이용하여 다음과 같이 유도된다.
| (4) |
| (5) |
| (6) |
| (7) |
식 (7)은 직선주행 및 제자리회전으로 이루어진 주행시 험경로에서 최종 방향각 오차는 주행거리와 회전각도에 비례하여 증가한다는 점을 나타낸다. 즉, 동일한 주행거리 와 회전각도가 동일하면 주행시험경로의 형상에 관계없이 방향각 오차가 동일하게 나타나게 된다.
2.2. 비시스템적 오차
실제 오도메트리를 사용할 때에는 식 (3)을 불연속식으 로 변환하여 사용한다.
| (8) |
식 (8)에서 Δs는 로봇의 이동거리, Δθ는 회전각도, Δsr 우 측 휠의 이동거리, Δsl은 좌측 휠의 이동거리, b는 휠 간격 을 나타낸다.
비시스템적 오차는 공분산 행렬을 이용해 나타내며, 식 (9)와 같다[5].
| (9) |
이때, Ft와 ∇uf는 식 (8)의 로봇 위치추정함수 f(xt, ut, t)의 자코비안을 의미한다.
공분산 행렬 Pt+1은 로봇과 노면간의 상호작용에 의한 비 시스템적 오차를 나타낸다. 또한, 식 (9)에서 첫 번째 항은 추정된 위치의 불확실성, 두 번째 항은 로봇 운동의 불확 실성에 각각 관련된다. 두 번째 항에서 좌우 휠의 운동에 대해 공분산 행렬 Σu는 다음 식 (10)과 같이 정의된다.
| (10) |
이때, kr과 kl은 로봇과 노면간의 상호작용에 대한 확률적 파라미터 즉, 비시스템적 오차 파라미터를 의미한다. 비시 스템적 오차 파라미터는 Chong[16]의 기법 등을 이용하여 실험적으로 확인할 수 있다. Chong[16]의 기법에서는 10m 직 선경로를 왕복 주행하고 최종 포즈 오차를 측정하고 최종 포즈 오차의 분포를 모델링하였다.
3. 주행시험경로 설계
3.1. 주행시험경로 설계시 고려사항
본 논문의 목표는 로봇의 시스템적 오차를 충분히 반영 할 수 있는 주행시험경로 설계기법을 제안하는 것이다. 오 도메트리 보정기법으로는 선행연구에서 제안한 Jung[19]의 기법을 사용한다.
Jung[19]의 기법에서는 로봇의 주요 오차 원인을 휠 직경 차이와 휠 간격 오차로 가정하고 있기 때문에 주행시험경 로는 직선주행과 제자리회전을 모두 포함하여야 한다. 또 한 최종 포즈 오차의 측정을 용이하기 하기 위해 시험경 로의 출발점과 도착점을 동일하게 설정하여야 한다. 이때, 로봇의 최종 방향각 오차는 식 (7)에서 보인 것과 같이 같 이 주행시험 경로의 총 주행거리와 회전각도가 동일하다 면 동일한 수준으로 나타난다. 따라서 주행시험경로의 형 상은 Fig. 2에 나타낸 것과 같은 정다각형 형태가 될 수 있 다. 본 논문에서는 정사각형 형태가 사용되었다.
식 (4) – (7)에는 휠 직경 및 간격오차에 의한 최종 포즈 오차 변화를 나타내었다. 시스템적 오차에 의한 최종 포즈 오차는 식 (4) – (7)에 나타낸 것과 같이 주행시험경로의 크 기에 비례하여 변화한다. 따라서 주행시험경로의 크기는 비시스템적 오차에 의한 최종 포즈 오차와 비교하여 시스 템적 오차에 의한 최종 포즈 오차를 최대로 할 수 있는 크 기이어야 한다. Jung[19]의 기법에서 로봇의 방향각 오차가 근사식 없이 계산된다. 하지만 주행시험경로가 지나치게 클 경우에는 요구되는 실험공간이 증가할 뿐만 아니라 다 양한 비시스템적 오차 원인의 영향을 받기 때문에 보정성 능의 향상을 보장할 수는 없다. 반면, 주행시험경로가 지 나지게 작을 경우에는 최종 포즈 오차가 매우 작게 나타 나게 되는데, 이는 오차 보정결과가 로봇 포즈의 측정 정 밀도에 민감하게 된다는 것을 의미한다.
3.2. 주행시험경로 설계기법
3.1절의 고려사항을 반영하여 제안하는 주행시험경로 설 계기법은 다음과 같이 요약할 수 있다
- 직선주행과 제자리회전을 포함하도록 주행시험경로 의 형상을 결정한다.
- 기 정의된 주행시험경로를 주행하여 시스템적 오차를 확인한다.
- 비시스템적 오차를 실험적으로 확인한다. Chong[16]의 기법 등이 사용될 수 있다.
- 시스템적 오차와 비시스템적 오차를 반영하여 주행시 뮬레이션을 수행한다
- 주행시뮬레이션 결과를 바탕으로 주행시험경로의 최 소 크기를 정한다.
이때, 주행시뮬레이션은 2) – 3)에서 확인한 시스템적 오차 와 비시스템적 오차 조건에서 주행시험경로의 크기를 변화 시키며 해당 크기에서의 기구학적 파라미터를 산출하는 단 계와 산출된 기구학적 파라미터를 이용하여 로봇을 보정한 후의 위치 오차를 산출하는 단계로 나누어진다. 주행시험경 로 크기의 결정은 보정 후 위치 오차를 비교하여 정한다.
4. 시뮬레이션 결과
제안하는 주행시험경로 설계기법을 이용하여 주행시험 경로의 설계조건을 획득하는 시뮬레이션을 수행하였다. 시 뮬레이션 로봇은 상용 이륜차동구동형로봇(TETRA-DS II)[20]를 참고하였으며, 주요 제원은 휠 직경 0.15m, 휠 간격 0.385m, 휠 너비 0.03m이다. 시뮬레이션에서 로봇의 위치 와 방향각은 기구학적 모델링 오차를 고려한 로봇 기구학 을 통해 계산되었다.
휠의 기구학적 모델링 오차는 파라미터 값을 설정하여 시뮬레이션에 반영하였으며, 기구학적 오차 파라미터는 Eb 와 Ed로 Borenstein[4]의 연구에서 정의한 것과 같다.
| (11) |
이때, bactual은 실제 휠 간격, bnominal은 로봇 제원 상의 휠 간격을, DR은 실제 우측 휠 직경을, DL은 실제 좌측 휠 직 경을 의미한다.
비시스템적 오차는 식 (10)의 공분산 행렬에 나타낸 비 시스템적 오차 파라미터 kr, kl을 이용하여 반영한다.
시뮬레이션 조건은 다음과 같다. 시스템적 오차 조건은 Eb = 1.025, Ed = 0.999, 비시스템적 오차 조건은 kr = kl = 1.00 ×10-6m이었다. 주행시험경로의 크기는 정사각형 경로의 한 변의 길이가 L≤10m인 범위를 고려하였다.
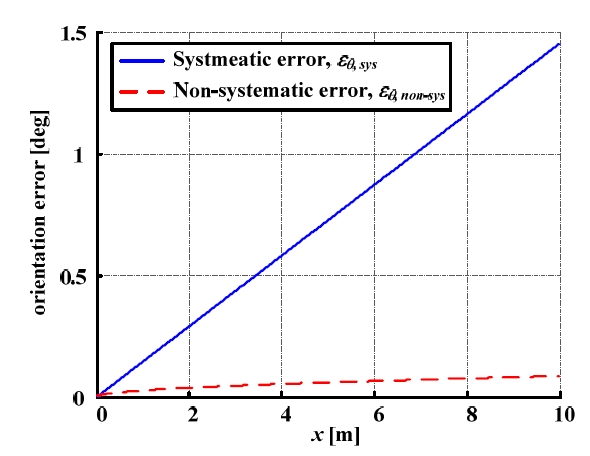
Fig. 3은 주행시험경로 중 직선 경로에서 시스템적 오차 에 의한 방향각 오차와 비시스템적 오차에 의한 방향각 오차를 비교한 결과이다. x-축은 주행시험경로의 한 변의 길이를 나타낸다. Fig. 3에서는 주행거리가 증가함에 따라 방향각 오차 또한 증가함을 확인할 수 있다.
실제 오도메트리 보정과정에서는 주행시험 후 전체 방 향각 오차 중에서 시스템적 오차에 의한 방향각 오차가 지배적인 것이 유리하다. 이때, 전체 방향각 오차는 시스 템적 오차에 의한 방향각 오차와 비시스템적 오차에 의한 방향각 오차의 합을 의미한다. 전체 방향각 오차 중에서 시스템적 오차에 의한 방향각 오차가 지배적이라는 것은 주행시험을 통해 오도메트리를 보정한 결과가 비시스템적 오차에 덜 민감하다는 것을 의미하기 때문이다. 따라서 전 체 방향각 오차 대비 시스템적 오차에 의한 방향각 오차 의 상대적 크기를 확인할 필요가 있다.
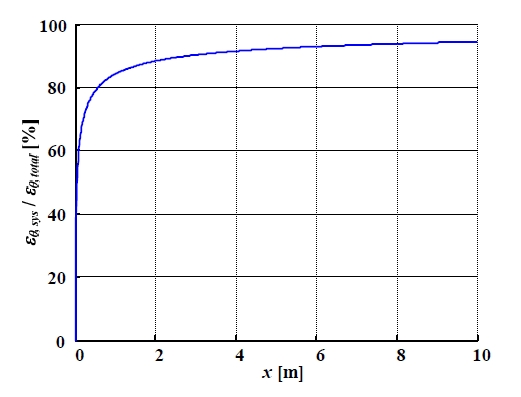
Fig. 4에는 전체 방향각 오차 대비 시스템적 오차에 의한 방향각 오차의 상대적인 크기를 나타내었다. 시뮬레이션 조건은 Fig. 3의 조건과 동일하다. Fig 4에서는 주행거리가 증가함에 따라 전체 방향각 오차 대비 시스템적 오차에 의한 방향각 오차의 상대적 크기 또한 증가함을 확인할 수 있다. 시뮬레이션 조건에서는 한 변의 길이가 4m일 때 전체 방향각 오차 대비 시스템적 오차에 의한 방향각 오 차의 상대적인 크기가 약 91%이었다.
Fig. 5는 오도메트리 보정 시뮬레이션 후의 평균 위치오 차를 나타낸다. 오도메트리 보정 시뮬레이션은 정사각형 경로의 한 변의 길이를 0.5m부터 10m까지 변화시키며 각 각의 주행시험경로에서 기구학적 파라미터를 산출한 후, 산출한 기구학적 파라미터를 반영하여 동일한 경로(4m× 4m 정사각형 경로)에서 보정 후 위치 오차를 비교하는 방 식으로 진행되었다. 시스템적 오차 조건은 Eb = 1.028, Ed = 0.999, 비시스템적 오차 조건은 kr = kl = 1.69×10-6m이었으며, 오도메트리 보정 시뮬레이션은 800회 반복하였다. 시뮬레 이션 결과, 보정 후의 위치 오차는 주행시험경로의 크기에 영향을 받는 것으로 확인되었다. Fig 5에서 0.5m×0.5m 경 로를 사용한 경우(주행거리가 2m)의 보정 후 위치 오차가 가장 큰 것으로 나타났다. 보정 후 위치 오차는 4m×4m 경로(주행거리가 16m)까지 감소하며, 이후 두드러지는 변 화가 나타나지 않았다. 따라서 시뮬레이션 조건에서 4m× 4m 경로, 즉 최소 주행거리 16m가 적절한 주행시험경로의 크기가 된다.
Fig. 6은 또한 오도메트리 보정 시뮬레이션 후의 평균 위 치 오차를 나타낸다. 오차 조건은 Fig. 5와 동일하다. 대신 보정에 사용되는 주행시험경로는 정팔각형 경로를 사용하 였다. 시뮬레이션 결과, Fig. 5와 유사한 경향성을 보였다. 주행거리가 2m (Fig. 5의 0.5m×0.5m 경로에 대응)인 경우 위치 오차가 가장 크게 나타났으며, 주행거리가 16m (Fig. 5 의 4m×4m 경로에 대응)이 될 때까지 위치오차가 감소하 였다. 이후에는 위치 오차의 두드러진 변화가 나타나지 않 았다. 따라서 주행시험경로의 형상에 무관하게 최소 주행 거리 16m는 유효한 설계조건임을 알 수 있다.
5. 실험 결과
Fig. 7은 실험 장비와 환경을 나타낸다. 로봇은 상용 이 륜차동구동형로봇인 TETRA-DS II[20]를 사용하였다. 또한, 로봇의 위치 및 방향각을 측정하기 위해 상용절대위치인 식센서인 STARGAZER[21]를 로봇에 설치하였다. 주행환경 은 비교적 평탄한 실내환경이었다.
주행시험경로 설계 시뮬레이션의 초기조건을 획득하기 위하여 예비실험을 수행하였다. 시스템적 오차 조건은 4m ×4m 정사각형 경로를 오픈-루프 제어로 주행시킨 후 최 종 포즈 오차를 측정하여 기구학적 파라미터를 확인하였 다. 비시스템적 오차 조건은 Chong[16]의 기법을 이용하여 확인하였다. 예비실험을 통해 확인한 오차 조건은 시스템 적 오차 Eb = 1.0255, Ed = 1.0017, 비시스템적 오차 kr = kl = 2.89×10-6m이었다.
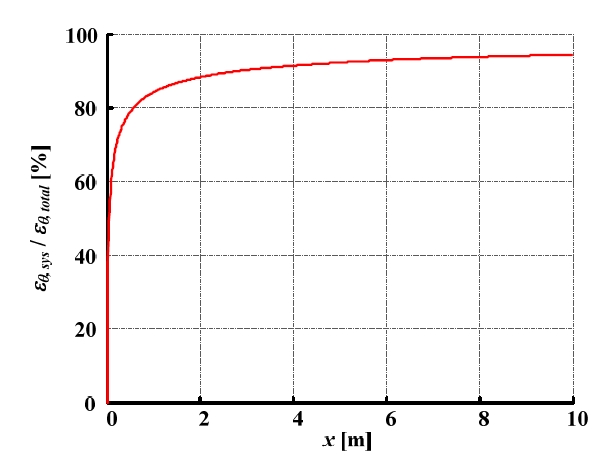
Fig. 8은 전제 방향각 오차 대비 시스템적 오차에 의한 방향각 오차의 상대적인 크기를 나타낸다. 예비실험에서 확인한 시스템적 오차 및 비시스템적 오차를 반영하였을 때, 4m×4m 경로에서 전체 방향각 오차 대비 시스템적 오차 에 의한 방향각 오차의 상대적인 크기가 약 91.5%이었다.
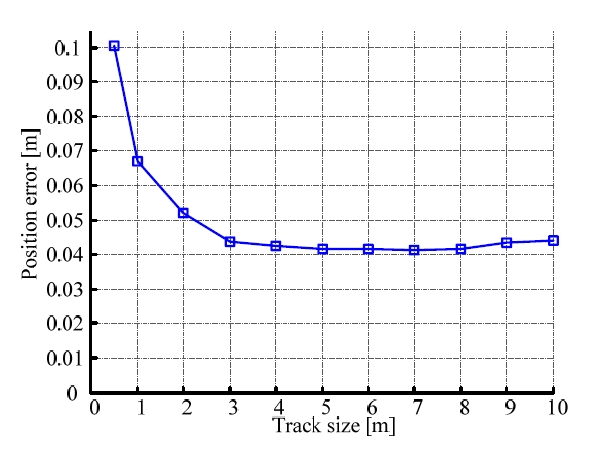
Fig. 9는 예비실험에서 확인한 오차 조건을 반영하여 오 도메트리 보정 시뮬레이션을 수행한 결과이다. Fig 8에서 0.5m×0.5m 경로를 사용한 경우의 보정 후 위치 오차가 가장 큰 것으로 나타났다. 보정 후 위치 오차는 4m×4m 경로까지 감소하며, 이후 한 변의 길이가 4m – 10m일 때에 는 두드러지는 변화가 나타나지 않았다. 따라서 실험 조건 에서는 4m×4m 경로, 즉 최소 주행거리 16m가 적절한 주 행시험경로의 크기가 된다.
오도메트리 보정 시뮬레이션을 통해 확인한 주행시험경 로의 조건이 실제로 유용한지 확인하기 위하여 세 가지 다른 주행시험경로를 이용하여 각각 오도메트리 보정을 수행하였다. 로봇을 2m×2m 경로, 4m×4m 경로, 6m×6m 경로를 따라 각각 오픈-루프 제어로 주행시킨 후 기구학적 파라미터를 산출하였다. 로봇은 각 주행 경로를 시계 및 반시계방향으로 주행하였으며, 비시스템적 오차의 영향을 고려하여 주행방향별로 5회씩 하고, 평균값을 오차 보정에 사용하였다. Table 1은 각 주행시험경로에서 획득한 기구학 적 파라미터를 나타낸다.
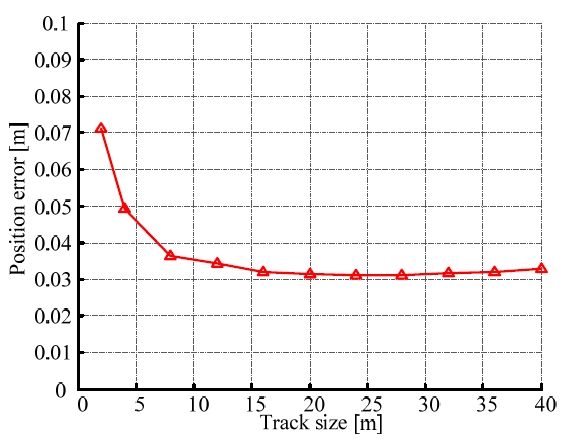
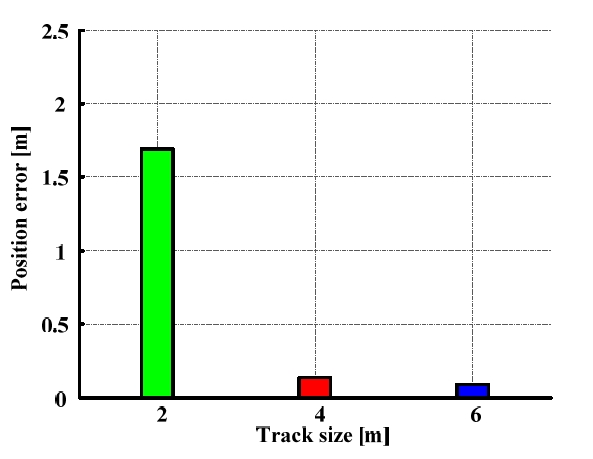
Fig. 10은 Table 1의 기구학적 파라미터를 이용하여 오도 메트리를 보정한 후의 위치 오차를 나타낸다. 보정 후의 로봇은 4m×4m 정사각형 경로를 반시계방향으로 주행하 였다. 2m×2m 경로를 사용하여 오도메트리를 보정한 경우 에는 위치 오차가 평균 1.69m로 나타났다. 4m×4m 경로를 사용하여 오도메트리를 보정한 경우에는 위치 오차가 평 균 0.14m로 2m×2m 경로에서 보정한 경우와 비교하여 오 차가 감소하였다. 6m×6m 경로에서 보정한 경우에는 위치 오차가 평균 0.09m로 4m×4m 경로에서 보정한 결과와 비 교적 유사한 수준의 오차를 보였다.
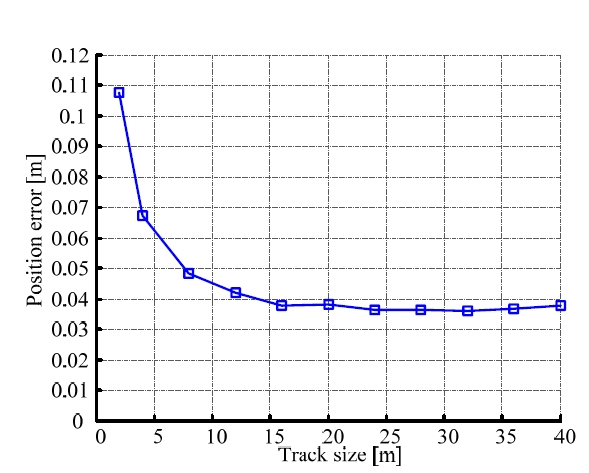
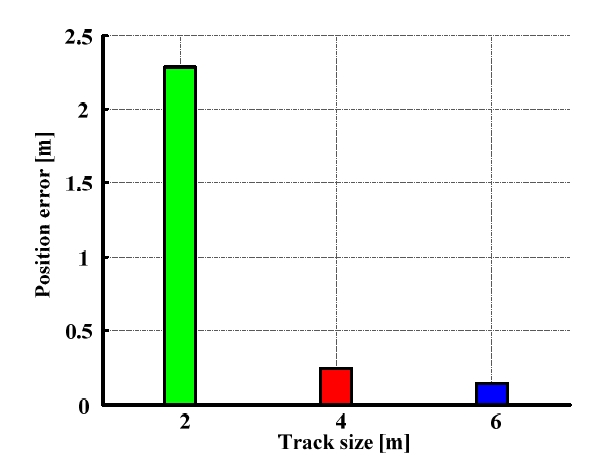
Fig. 11은 Table 1의 기구학적 파라미터를 이용하여 오도 메트리를 보정한 후의 위치 오차를 나타낸다. 보정 후의 로봇은 한 변의 길이가 5m인 정삼각형 경로를 시계방향으 로 주행하였다. 2m×2m 경로에서 오도메트리를 보정한 경 우에는 위치 오차가 평균 2.28m로 나타났다. 4m×4m 경로 를 사용하여 오도메트리를 보정한 경우에는 위치 오차가 평균 0.24m로 2m×2m 경로에서 보정한 경우와 비교하여 오차가 감소하였다. 6m×6m 경로에서 보정한 경우에는 위 치 오차가 평균 0.14m로 4m×4m 경로에서 보정한 결과와 비교적 유사한 수준의 오차를 보였다.
Fig. 10-11에 나타낸 주행시험경로 별 위치 오차의 차이 가 통계적으로 의미가 있는지 확인하기 위하여 독립 표본 t-검정[22]을 수행하였다.
Table 2는 Fig 10에 나타낸 주행시험경로 별 위치 오차를 독립 표본 t-검정으로 분석한 결과이다. 독립 표본 t-검정에 서 유의확률 p가 0.05 이하이면 두 집단의 평균은 통계적 으로 다른 값이라고 해석할 수 있다. 먼저 2m×2m 경로와 4m×4m 경로를 비교한 결과, 두 경우의 위치 오차는 유의 확률 p가 0.05 이하로 통계적으로 다른 값이라는 결과를 얻었다. 반면 6m×6m 경로와 4m×4m 경로를 비교한 결과, 두 경우의 위치 오차는 유의확률 p가 0.408로 통계적으로 차이가 있는 값은 아니었다.
Table 3는 Fig. 11에 나타낸 주행시험경로 별 위치 오차를 독립 표본 t-검정으로 분석한 결과이다. 먼저 2m×2m 경로 와 4m×4m 경로를 비교한 결과, 두 경우의 위치 오차는 유의확률 p가 0.05 이하로 통계적으로 다른 값이라는 결과 를 얻었다. 반면 6m×6m 경로와 4m×4m 경로를 비교한 결과, 두 경우의 위치 오차는 유의확률 p가 0.121로 통계적 으로 차이가 있는 값은 아니었다. 따라서 제안하는 주행시 험경로 설계기법을 이용하여 얻은 4m×4m 경로, 즉 최소 주행거리 16m는 주행시험경로로서 적합함을 확인하였다.
6. 결 론
본 논문에서는 오도메트리 보정실험을 위한 주행시험경 로 설계기법을 제안하였다. 로봇 오도메트리의 시스템적 오차는 주행시험 후 최종 포즈 오차에 반영되어 나타나기 때문에 최종 포즈 오차에 영향을 미치는 주행시험경로의 형상과 크기는 오도메트리 보정 정밀도에 중대한 영향을 미친다. 주행시험경로는 로봇의 크기, 보정기법, 시스템적 오차 및 비시스템적 오차를 고려하여 신중하게 결정되어 야 한다. 주행시험경로 설계간 고려사항을 반영하여 본 논 문에서는 주행시험경로의 형상으로서 정다각형 형태를 제 안하였다. 또한, 주행시험경로의 최소크기를 결정하기 위 하여 주행시뮬레이션을 통해 전체 방향각 오차 대비 시스 템적 오차에 의한 방향각 오차의 상대적 크기와 보정 후 위치 오차를 비교하였다. 제안하는 주행시험설계기법은 시 뮬레이션과 실험을 통해 증명되었다.
REFERENCES
-
Choi, S.-H, Kim, Y.-K, Hwang, Y.-S, Kim, H.-W, Lee, J.-M, "EKF Based Outdoor Positioning System using Multiple GPS Receivers", Journal of Korea Robotics Society, (2013), 8, p129-135.
[https://doi.org/10.7746/jkros.2013.8.2.129]

-
Noh, C.-B, Kim, M.-H, Lee, M.-C, "Path Planning for the Shortest Driving Time Considering UGV Driving Characteristic and Driving Time and Its Driving Algorithm", Journal of Korea Robotics Society, (2013), 8, p43-50.
[https://doi.org/10.7746/jkros.2013.8.1.043]

-
Borenstein, J, Everett, H, Feng, L, Where am I? Sensors and methods for mobile robot positioning, University of Michigan, (1996).
[https://doi.org/]

-
Borenstein, J, Feng, L, "Measurement and correction of systematic odometry errors in mobile robots", IEEE Transactions on Robotics and Automation, (1996), 12(6), p869-880.
[https://doi.org/10.1109/70.544770]

-
Siegwart, R, Nourbakhsh, I. R, Scaramuzza, D, Introduction to autonomous mobile robots, (2011), The MIT Press.
[https://doi.org/]

-
Thrun, S, Burgard, W, Fox, D, Probabilistic robotics, (2005), The MIT Press.
[https://doi.org/]

-
Abbas, T, Arif, M, Ahmed, W, , "Measurement and correction of systematic odometry errors caused by kinematics imperfections in mobile robots", (2006), SICEICASE International Joint Conference, p2073-2078.
[https://doi.org/]

-
Martinelli, A, "The odometry error of a mobile robot with a synchronous drive system", IEEE Transactions on Robotics and Automation, (2002), 18(3), p399-405.
[https://doi.org/10.1109/tra.2002.1019477]

-
Martinelli, A, Tomatis, N, Siegwart, R, "Simultaneous localization and odometry self calibration for mobile robot", Autonomous Robots, (2007), 22(1), p75-85.
[https://doi.org/10.1007/s10514-006-9006-7]

-
Antonelli, G, Chiaverini, S, Fusco, G, "A calibration method for odometry of mobile robots based on the leastsquares technique: theory and experimental validation", IEEE Transactions on Robotics, (2005), 21(5), p994-1004.
[https://doi.org/10.1109/tro.2005.851382]

-
Antonelli, G, Chiaverini, S, "Linear estimation of the physical odometric parameters for differential-drive mobile robots", Autonomous Robots, (2007), 23, p59-68.
[https://doi.org/10.1007/s10514-007-9030-2]

-
Censi, A, Marchionni, L, Oriolo, G, "Simultaneous maximum-likelihood calibration of odometry and sensor parameters", (2008), IEEE International Conference on Robotics and Automation, p2098-2103.
[https://doi.org/10.1109/robot.2008.4543516]

-
Antonelli, G, Caccavale, F, Grossi, F, Marino, A, "A non-iterative and effective procedure for simultaneous odometry and camera calibration for a differential drive mobile robot based on the singular value decomposition", Intelligent Service Robotics, (2010), 3(3), p163-173.
[https://doi.org/10.1007/s11370-010-0067-2]

-
Borenstein, J, Feng, L, "Gyrodometry: A new method for combining data from gyros and odometry in mobile robots", (1996), IEEE International Conference on Robotics and Automation, p423-428.
[https://doi.org/10.1109/robot.1996.503813]

-
Komoriya, K, Oyama, E, "Position estimation of a mobile robot using optical fiber gyroscope (OFG)", (1994), IEEE/RSJ International Conference on Intelligent Robots and Systems, p143-149.
[https://doi.org/10.1109/iros.1994.407398]

-
Chong, K.S, Kleeman, L, "Accurate odometry and error modelling for a mobile robot", (1997), IEEE International Conference on Robotics and Automation, p2783-2788.
[https://doi.org/10.1109/robot.1997.606708]

-
Lee, K, Jung, C, Chung, W, "Accurate calibration of kinematic parameters for two wheel differential mobile robots", Journal of mechanical science and technology, (2011), 25(6), p1603-1611.
[https://doi.org/10.1007/s12206-011-0334-y]

-
Jung, C, Chung, W, "Design of Test Tracks for Odometry Calibration of Wheeled Mobile Robots", International Journal of Advanced Robotic Systems, (2011), 8(4), p1-9.
[https://doi.org/10.5772/45712]

-
Jung, C, Chung, W, "Accurate calibration of two wheel differential mobile robots by using experimental heading errors", (2012), IEEE International Conference on Robotics and Automation, p4533-4538.
[https://doi.org/10.1109/icra.2012.6224660]

-
Dongbu Robot Co. Ltd, Available: http://www.dongburobot.com.
[https://doi.org/]

-
HAGISONIC Co. Ltd, Available: http://www.hagisonic.com.
[https://doi.org/]

-
Peck, R, Olsen, C, Devore, J. L, Introduction to Statistics and Data Analysis, Cengage Learning, (2011).
[https://doi.org/]