유연관절로봇의 모터 동역학을 정확하게 재설정하기 위한 적분매니폴드 피드백제어 개발

1. 서 론

모든 관절에 관절토크센서(joint-torque sensor)가 장착된 유연관절로봇(flexible-joint robot)은, 뒤에서 설명할 유연관절 로봇의 모델에서 볼 수 있듯이, 크게 모터부분 동역학 (motor-side dynamics)과 링크부분 동역학(link-side dynamics) 으로 구성된다. 이로 인해 일반적으로 N개의 관절로 된 유 연관절로봇은 2N개의 자유도를 갖는 불충분구동시스템 (under-actuated system)이며, 매우 복잡한 동역학을 보인다^[1]. 이런 시스템의 복잡성과 불충분한 구동 능력을 극복하기 위해서, 유연관절로봇의 제어에서 정확한 모델을 확보할 수 있는지의 여부는 일반적인 강관절로봇(rigid-joint robot) 에서보다 훨씬 중요하다. 심지어 적용 분야에 따라서는, 유연관절로봇의 정확한 모델을 확보하는 것이 단지 제어 기의 성능을 높이는 것이 아니라 유연관절로봇의 제어기 를 완성하는데 필수적인 경우도 있다^[2-4]. 이와 같은 관점에 서 유연관절로봇의 정확한 모델을 구하기 위한 연구는 중 요해진다.

그러나 유연관절로봇 시스템의 복잡성으로 인해 유연관 절로봇 모델을 정확히 구하는 것은 매우 어렵다. 예를 들 어 로봇의 동역학이 매우 복잡하기 때문에 시스템식별 (system identification)을 통해 모델을 알아내는 것이 쉽지 않 으며^[5], 외란관측기(disturbance observer)와 같은 강인제어를 사용한 외란 및 모델 불확실성 보상방법^[6]도 유연관절로봇 의 불충분구동구조와 비선형성으로 인해 직접적으로 적용 하기 힘들다.

실제 적용의 측면에서 유연관절로봇의 모델을 모터부분 동역학과 링크부분 동역학으로 나누어 각각의 모델을 구 하는 것이 더 쉬울 수 있다. 실제로 링크부분 동역학에 해 당하는 매니퓰레이터 동역학의 경우, CAD 데이터를 통해 서 비교적 정확하게 구할 수 있다. 그러나 모터부분 동역 학의 경우, 간단한 구조임에도 불구하고 모터 부분에 존재 하는 측정할 수 없는 외란으로 인해 정확한 모델을 구하 기 힘든 경우가 많다. 특히 하모닉 드라이브(harmonic drive) 와 같은 감속기가 적용된 경우, 감속기로 인한 비선형성과 외란(예를 들어 쿨롱마찰력(Coulomb friction), 스틱션 (stiction) 등)으로 인해 정밀한 모터 동역학 모델을 얻기 쉽 지 않다^[4]. 하지만 모터부분만을 놓고 본다면 불충분구동 시스템이 아니기 때문에 이러한 외란은 보상이 가능하다. 물론 유연관절로봇의 모터부분 동역학과 링크부분 동역학 은 관절토크센서를 통해 서로 연결되어 있기 때문에 모터 부분에 존재하는 외란을 제거하려는 시도는 자칫 링크부 분 혹은 시스템 전체의 거동을 불안정하게 만들 가능성이 있다. 그러나 유연관절로봇의 구조를 잘 활용하면 추가적 인 불안정성은 야기하지 않고 외란을 보상할 수 있다. 실 제로 외란관측기를 참고하여 마찰관측기(friction observer)를 만들어서 마찰력을 보상하거나^[7] 확장상태관측기(extended state observer, ESO)를 활용하여 외란을 보상할 수 있다^[8]. 더 나아가 모터 외란을 보상하고 모터 동역학의 모델 불 확실성을 적극적으로 극복하기 위하여 유연관절로봇의 모 터부분에 대해서만 외란관측기를 적용하기도 한다^[9-11]. 이 러한 방법들은 유연관절로봇에서 모델 정보를 획득하는데 많은 도움이 된다.

외란관측기 등을 활용한 모터부분 외란 및 모델 불확실 성 보상방법은 말 그대로 보상이기 때문에 모터부분 동역 학 자체를 바꾸는 데는 한계가 있다. 특히 외란관측기를 활용하는 경우 고이득제어기(high gain controller)의 특성으 로 인해 설정한 명목시스템(nominal system)과 대상시스템 의 차이가 클 경우 시스템을 불안정하게 만들 수 있다. 유 연관절로봇에서 모터부분과 링크부분의 연결성을 생각한 다면 이는 큰 문제가 될 수 있다.

최근 들어 ^[1]에서 제시된 연구는 모터부분 동역학을 변 경하는 것이 가능함을 시사한다. 즉, 만약 관절토크를 측 정하여 음성 피드백을 할 수 있다면, 모터의 관성모멘트를 더 작은 값으로 줄일 수 있으며, 모터부분 마찰력을 감소 시키고 관절탄성진동(joint elastic oscillation)을 억제할 수 있 다 ^[1]. 관성모멘트는 외부토크에 대한 시스템의 동작특성을 나타낸다. 모터 동역학에서 보면 관절토크는 일종의 외력 이기 때문에 피드백을 통해 시스템에 작용하는 관절토크 를 적절하게 조절해줌으로써 모터부분이 다른 관성모멘트 를 가지도록 만들 수 있다. 모터의 관절 모멘트를 변경할 수 있는 것은 곧 모터부분 동역학 자체를 변경할 수 있다 는 것을 의미한다. 따라서 이 연구결과는 모터부분 외란 등의 단순 보상뿐만 아니라 유연관절로봇의 모터부분 동 역학을 재설정하는 것이 비교적 쉽게 가능하다는 것을 시 사한다.

그러나 이런 관절토크 피드백방법^[1]은 모터 마찰력과 같 은 모터 외란이 있는 경우 모터의 관성모멘트를 줄이는 것과 관련하여 제한된 성능을 보인다. 이는 뒤에서 이론과 실험 결과를 통하여도 확인할 수 있다. 본 논문에서는 ^[1] 에서 제시된 관절토크를 피드백하는 방법을 확장하여 모 터 동역학을 재설정(reshaping)하기 위하여 적분매니폴드 피드백제어(integral manifold feedback control, IMFC)기법을 제 안한다. IMFC는 모터 외란에 의한 영향을 극복하고, 모터 동역학을 정확하게 재설정할 수 있다. 특히 관성모멘트의 경우 기존의 외란관측기와는 다르게 실제 시스템의 30% 가 되도록 줄여도 불안정성을 야기하지 않고 작동한다. 본 논문에서는 IMFC의 외란에 대한 강인성을 이론적으로 증 명하고, 모터 동역학에 대한 재설정성능을 실험장치를 이 용하여 실험적으로 검증한다.

본 논문의 2장에서는 개발한 IMFC에 대해서 소개하며, 3장에서는 IMFC의 모터 외란에 대한 강인성을 이론적으 로 증명한다. 4장에서는 개발한 IMFC의 모터 동역학 재설 정성능을 확인하기 위해 사용한 실험 장치 및 실험결과를 제시하며, 마지막으로 5장의 결론을 통해 정리한다.

2. 모터 동역학 재설정을 위한 IMFC 설계

이 장에서는 개발한 IMFC에 대해서 자세히 소개한다. 가정한 유연관절로봇의 모델을 제시하고, 그 모델에서 모 터부분 동역학만을 재설정하기 위해서 IMFC를 어떻게 설 계하였는지 설명한다.

2.1. 유연관절로봇 모델링

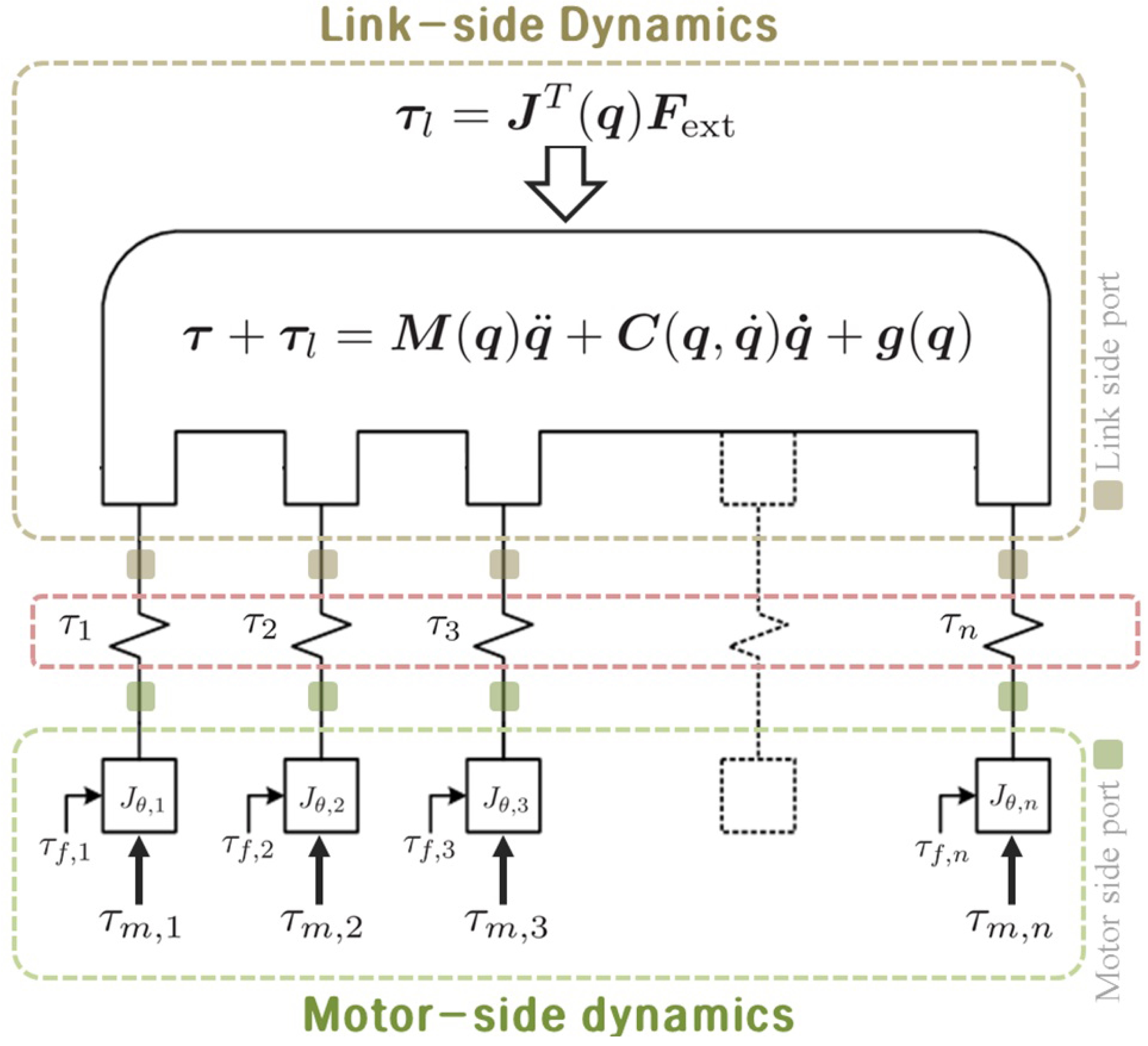
N자유도 유연관절로봇은 그림 1에서와 같이 관절토크센 서를 중심으로 모터부분 동역학(motor-side dynamics)과 링 크부분 동역학(link-side dynamics)으로 구성된다고 모델링 할 수 있다. 링크부분 동역학은 일반적인 매니퓰레이터 동 역학과 유사하다. 단 매니퓰레이터 동역학의 관성행렬 M(q)는 모터질량에 의한 효과도 포함하고 있다. 모터부 분 동역학은 서로 독립된 N개의 1자유도 모터 동역학으로 모델링 된다. 모터 동역학 자체는 매우 단순하지만, 모터 와 감속기에서 발생하는 마찰력과 같은 외력 (τ_ƒ ) 을 고려 해야 하기 때문에 모델이 복잡해진다.

Fig. 1

Lumped parameter model of flexible-joint robot.

제안한 모델을 고려하여 유연관절로봇의 동역학을 유도 하면 다음과 같다^[1].

$$ M\left(q\right)\stackrel{..}{q}+C\left(q,\stackrel{.}{q}\right)\stackrel{.}{q}+g\left(q\right)=\mathit{\tau }+{\mathit{\tau }}_l$$

(1)

$$ M_{\mathit{\theta }}\stackrel{..}{\mathit{\theta }}+\mathit{\tau }={\mathit{\tau }}_m+{\mathit{\tau }}_f$$

(2)

여기서 q∈ℝ n은 매니퓰레이터 관절각도를 나타내는 벡 터이며, θ∈ℝ n은 해당관절에서의 모터각도를 나타내는 벡터이다. Mq∈ℝ n×n은 매니퓰레이터 관성행렬 (manipulator inertia matrix)를 의미하며, Cq,q.∈ℝ n×n은 원 심력 및 코리올리 효과(centrifugal and Coriolis effect)를 나 타내며, Mθ∈ℝ n×n는 관절토크센서에서 바라본 각 모터 의 관성모멘트를 대각성분으로 갖는 대각행렬이다. gq∈ℝ n은 중력에 의한 토크를 의미한다. τm∈ℝ n은 관 절구동모터의 구동토크를 나타내는 벡터이며, τl∈ℝ n은 매니퓰레이터 쪽으로 들어오는 외력에 의한 토크(external link torque)를 의미한다. τf∈ℝ n은 모터에 작용하는 마찰 력에 의한 토크를 나타낸다. 끝으로 τ∈ℝ n은 관절토크센 서를 통해 얻어지는 센서토크로, 관절토크센서의 강성계 수(stiffness)를 대각성분으로 갖는 대각행렬 K∈ℝ n×n 에 대하여 τ = K(θ−q) 로 표현된다. 이 모델을 기반으로 제 어기를 설계한다.

2.2. IMFC 설계

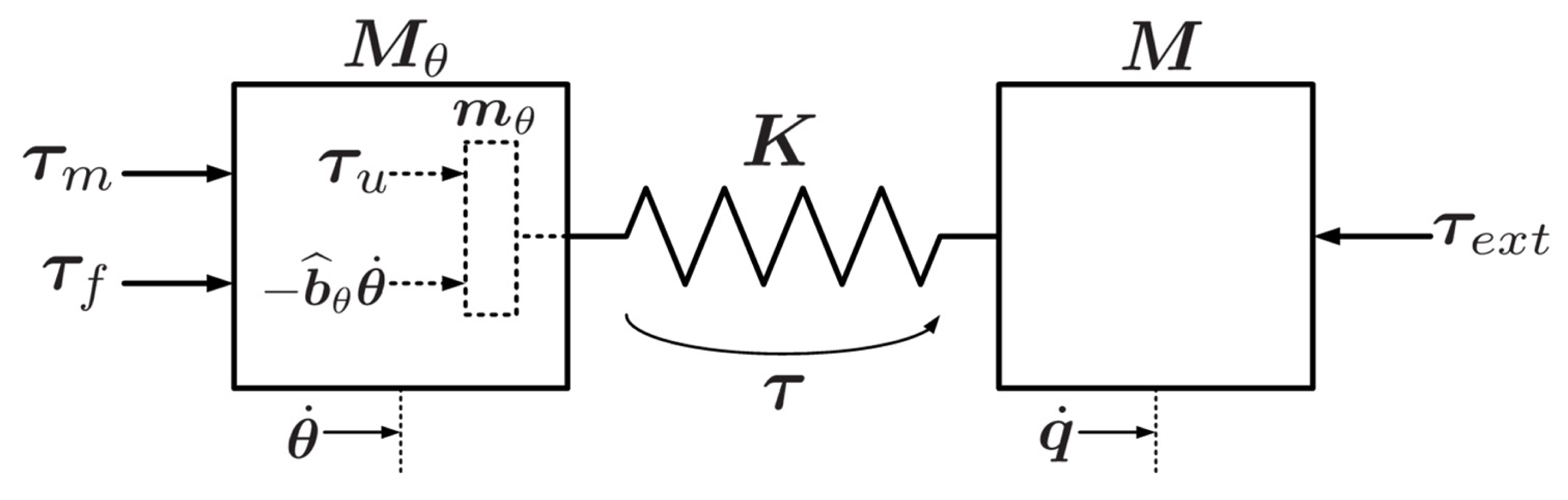
모터 동역학을 재설정한다는 것은 그림 2에서와 같이 유연관절로봇의 모터부분 동역학 (2)를 사용자가 정의한 (혹은 원하는) 동역학, 예를 들어 mθθ..+τ=τu 으로 변형 할 수 있다는 것을 의미한다. 앞에서 설명한 바와 같이 유 연관절로봇은 불충분구동시스템이기 때문에 유연관절로봇 의 전체 동역학을 재설정할 수는 없다. 따라서 본 논문에 서는 그림 2에서와 같이 링크부분 동역학은 그대로 둔 상 태에서 모터가 더 작은 관성모멘트를 갖고 사용자가 설정 한 마찰력만을 가질 수 있도록 모터 동역학만을 재설정하 는 문제를 다룬다. 모터 동역학이 사용자가 정의한 (혹은 원하는) 대각 관성모멘트행렬 mθ=mθT 을 갖도록 IMFC 를 다음과 같이 설계한다:

$$ {\mathit{\tau }}_m={\stackrel{\wedge }{M}}_{\mathit{\theta }}{m}_{\mathit{\theta }}^{-1}{\mathit{\tau }}_u+\left(I-{\stackrel{\wedge }{M}}_{\mathit{\theta }}{m}_{\mathit{\theta }}^{-1}\right)\mathit{\tau }+{\stackrel{\wedge }{M}}_{\mathit{\theta }}{m}_{\mathit{\theta }}^{-1}{K}_I\left\{\int \left({\mathit{\tau }}_u-\mathit{\tau }\right)\mathit{dt}-m_{\mathit{\theta }}\stackrel{.}{\mathit{\theta }}\right\}$$

(3)

Fig. 2

Motor dynamics reshaping from Mθ to mθ for one-dimensional case

여기서 τ_u 는 새로운 커맨드 입력을 의미하고, K_I 는 대 각 적분매니폴드 피드백이득행렬(integral manifold gain matrix)를 의미하며, M∧θ≥Mθ 는 사용자가 알 수 있는 M_θ 의 명목값을 나타낸다. 모터 동역학을 재설정하기 위해 제안한 IMFC는 대상시스템의 관성모멘트 정보 (M_θ) 를 요구하며, 보통 시스템식별을 통해 획득한 값을 사용하면 된다. 그러나 엄밀히 이야기를 하면 이렇게 얻 은 값은 실제 값과 차이가 있다. 이론적인 엄밀성을 위해 이 장에서는 실제 모터 관성모멘트 M_θ 와 그 명목값 M∧θ 을 구분하여 고려한다. IMFC의 강인성으로 인해, M∧θ 사용으로 인한 모델 불확실성으로 인한 효과도 극 복 가능하다.

3. 모터 외란에 대한 IMFC의 강인성

이 장에서는 모터 외란이 있는 상황에서 제안한 IMFC 가 정확한 재설정을 할 수 있는지 이론적으로 분석한다. 개발한 (3)을 (2)에 적용하면, 다음과 같은 폐루프 모터 동 역학(closed-loop motor dynamics)을 얻는다.

여기서 s=mθθ.+∫τ-τudt 는 적분매니폴드 (integral (sliding) manifold)이며, τw=τf-Mθ-M∧θθ.. 은 마찰력 및 모델 불확실성을 포함한 모터 부분에서의 모터 외란을 나타낸다. 적분매니폴드는 사용자 정의 동역학과 새로운 커맨드입력 사이의 오차의 적분으로 된 복합 토크오차다. 사용자 정의 동역학의 적분이므로 현재속도와 토크오차의 적분 값으로 구성되며, 따라서 동역학에 해당하는 양을 피 드백 하면서도 인과성(causality)을 유지하면서 구현 가능하 다. IMFC는 (3)에서와 같이 적분매니폴드를 직접 음성 피 드백을 하므로, 결과적으로 모터부분에 현재속도를 음성 피드백을 하는 것이기 때문에 물리적으로 보면 댐핑을 추 가하는 효과가 있어 시스템을 안정적으로 만든다.

유도된 (4)에서, 모터 동역학을 mθθ..+τ=τu 으로 재설 정한다는 것1 은 s.=0 을 의미한다. 이를 위해 제안한 IMFC는 1) 관절토크 피드백(joint torque feedback)과 2) 적분 매니폴드 피드백(integral manifold feedback)의 두 가지 피드 백 요소를 제공한다.

3.2. 적분매니폴드 피드백이 적용된 경우

모터 외란에 의한 영향을 극복하기 위해, 적분매니폴드 접근방법(integral manifold approach)를 활용하여 제어기를 개발하였다. 이런 제어기로는 대표적으로 적분슬라이딩매 니폴드 제어(integral sliding manifold control)가 있으며, 외란 에 대해 매우 강인한 특성을 보인다^[12]. IMFC의 적분매니 폴드 피드백도 이러한 개념을 기반으로 설계가 되었다. 다 만 기존에는 적분매니폴드에 대한 스위칭 제어가 적용되 는데 반해^[12], IMFC에서는 적분매니폴드가 직접 피드백 되 는 상황임에도 강인성이 유지된다는 점에서 특색을 지닌 다. 또한 적분매니폴드 s 역시 대상 시스템인 모터부분 동역학 (2)을 사용하여 정의하는 것이 아니라 관절토크 피 드백을 통해 변경된 모터 동역학(혹은 사용자가 정의한 모 터 동역학)을 이용하여 정의된다.

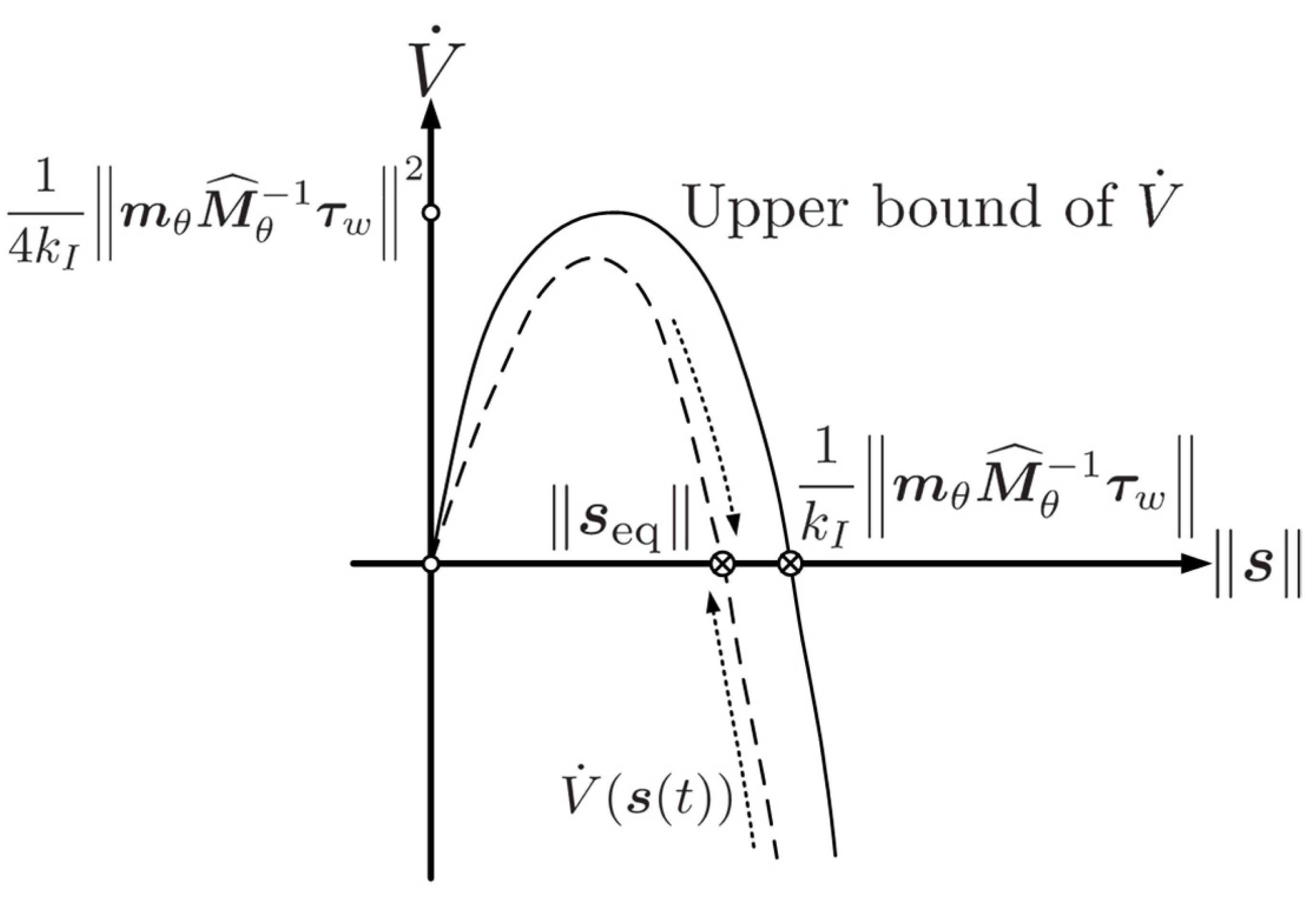
적분매니폴드 피드백으로 인해, 만약 피드백이득 K_I 가 충분히 크다면, s. 이 0 으로 수렴한다. 이를 확인하기 위 해서 유사 리야프노프함수(Lyapunov-like function) Vs=12sTs 를 고려한다. V(s)는 s ≠ 0 인 모든 s에 대하여 양의 값을 가지며(positive definite), 그 시간에 대한 미분은 다음과 같이 주어진다:

$$ \stackrel{.}{V}=s^T\stackrel{.}{s}=-s^T{K}_{I}s+s^T{m}_{\mathit{\theta }}{\stackrel{\wedge }{M}}_{\mathit{\theta }}^{-1}{\mathit{\tau }}_w=-{\left(s-\frac{1}{2}{K}_I^{-1}{m}_{\mathit{\theta }}{\stackrel{\wedge }{M}}_{\mathit{\theta }}^{-1}{\mathit{\tau }}_w\right)}^T{K}_I\left(s-\frac{1}{2}{K}_I^{-1}{m}_{\mathit{\theta }}{\stackrel{\wedge }{M}}_{\mathit{\theta }}^{-1}{\mathit{\tau }}_w\right)+\frac{1}{4}{\mathit{\tau }}_w^T{\stackrel{\wedge }{M}}_{\mathit{\theta }}^{-1}{m}_{\mathit{\theta }}{K}_I^{-1}{m}_{\mathit{\theta }}{\stackrel{\wedge }{M}}_{\mathit{\theta }}^{-1}{\mathit{\tau }}_w\le -K_I{\left(‖s‖-\frac{1}{{2k}_I}‖m_{\mathit{\theta }}{\stackrel{\wedge }{M}}_{\mathit{\theta }}^{-1}{\mathit{\tau }}_w‖\right)}^2+\frac{1}{{4k}_I}{‖m_{\mathit{\theta }}{\stackrel{\wedge }{M}}_{\mathit{\theta }}^{-1}{\mathit{\tau }}_w‖}^2$$

(5)

여기서 k_I 는 K_I 의 대각성분 중 최소값이며, ││s││ 는 유클 리드 놈(Euclidean norm)을 나타낸다. V. 를 그래프로 표현 한 그림 3에서 보면 알 수 있듯이, V. 의 구조적인 특성으 로 인해 적분매니폴드 s 는 평형점(equilibrium point)인 seq=KI-1mθM∧θ-1τw 로 수렴한다. 좀 더 자세히 살펴보면, s < s_eq 인 구간에서는 V. 이 양수이기 때문에 s는 커지게 되고, s > s_eq 인 구간에서는 V. 이 음수이기 때문에 s 는 작아지게 된다. s = s_eq 인 구간에서 V. 이 0 이 되며, 따라 서 이후 시스템은 슬라이딩 매니폴드 s = s_eq 위를 유영하 게 된다. 이때 IMFC 제어입력 (3)은 유한한 값을 가지므로 시스템은 안정적으로 동작한다. IMFC에서 적분매니폴드를 직접적으로 피드백 한 결과, 일반적인 슬라이딩모드 제어 에서처럼^[12]s = 0 이 아니라 다른 위치로 수렴하게 되는 것을 볼 수 있다. 여기서 중요한 점은 직접 피드백을 통해 얻어지는 평형점 s = s_eq 위에서는 원하는 재설정 동역학인 s.=0을 만족한다는 것이다 s.=-KIseq+mθM∧θ-1τw=0. 따라서 적분 매니폴드 피드백으로 인해 정확하게 모터 동 역학을 재설정할 수 있게 된다.

Fig. 3

The behavior of V. and its upper-bound with respect to ||s||

만약 모터 외란 τ_w 가 변하게 된다면, 물론 이 경우에도 V. 의 구조적인 특성으로 인해 s 는 새로운 s_eq 로 수렴하 게 되겠지만, 그 천이과정(transient motion) 동안에는 s.≠0을 만족한다고 보장할 수 없다. 그러나 피드백이득 K_I 를 증가시키면 외란에 의한 s_eq 변화 자체를 줄일 수 있으며 seq∝KI-1 동시에 (5)에서 볼 수 있듯이 s 에서 s_eq 로의 수렴속도(rate of convergence)도 증가시킬 수 있으므로, s. 을 빠르게 0 으로 보낼 수 있다. 따라서 K_I 를 충분히 증가시 킬 수 있다면, 모터 외란에 상관없이 IMFC를 이용하여 모 터 동역학을 정확하게 재설정할 수 있다.

4. 유연관절로봇을 이용한 중력 하에서의 실험

제안한 IMFC의 성능을 검증하기 위하여 1자유도 유연 관절로봇에 대하여 중력 하에서 실험을 수행하였다. 이 장 에서는 사용한 유연관절로봇에 대해 소개하고, 실험 결과 를 통해 IMFC의 모터 동역학 재설정성능을 제시한다.

4.1. 1자유도 유연관절로봇

실험에서는 그림 4와 같이 진자와 유사한 구성을 갖는 1자유도 유연관절로봇을 활용하였다. 두 개의 바디, 즉 M_θ 와 M 은 각각 모터부분 바디과 링크부분 바디를 의 미한다. 좀 더 가정한 관절토크센서 모델에 가깝고, 그리 고 깨끗한 신호를 얻기 위하여 상용 관절토크센서를 사용 하지 않고 유연피벗(flexure pivot)을 활용하여 비틀림스프링 을 제작하여 관절토크센서로 활용하였다^[13]. 유한요소해석 (finite element method, FEM)을 통하여 사용한 모터의 구동 출력범위 내에서 모든 박형 외팔보 (cantilever blade)의 변형 이 탄성영역 안에서만 일어나도록 설계하였으며, 그 결과 전체 구동범위가 (±16°) 인 매우 소프트한 관절토크센서 를 얻을 수 있었다. 구동을 위하여 AC 모터(Yaskawa Σ-V motor, SGMJV-04, rated torque: 1.27Nm, rated speed: 3000 rpm) 를 사용하였고, 두 개의 광학 엔코더 (optical encoder, USDIGITAL, E6-2500-236, 2500 CPR)를 각 부분에 장착하여 모터각도 θ 와 링크각도 q 를 측정하였다. 센서토크 τ 는 두 각도의 차이를 통하여 계산하였다. 나머지 시스템 파라 미터는 표 1에서 확인할 수 있다.

Fig. 4

Details of the one degree-of-freedom flexible-joint robot

Table 1

System parameters

4.2. 모터 동역학 재설정 실험

IMFC를 적용하기 위해 (3)에서 mθMθ-1=0.3 으로 설정 하고 새로운 커맨드입력 τu=τstep-bθθ.을 입력하였다. 여 기서 τ_step 은 0.08 N-m 의 유사스텝입력이며, b_θ 는 사용 자정의 점성마찰계수이다. 제안한 IMFC의 경우 오직 모터 부분 동역학만을 바꿀 뿐 링크부분 동역학은 바꾸지 않기 때문에 시스템은 τ_step 으로 인해 중력 하에서의 전형적인 진자운동을 보이며, 이것이 전체 시스템의 거동을 결정한 다. 그러나 세부적인 모터의 움직임은 모터 동역학이 변함 에 따라 분명한 차이가 나타난다. 예를 들어 만약 IMFC가 기대한대로 동작을 하게 되면, 모터 동역학은 다음과 같이 주어지게 된다.

$$ m_{\mathit{\theta }}\stackrel{..}{\mathit{\theta }}+b_{\mathit{\theta }}\stackrel{.}{\mathit{\theta }}+\mathit{\tau }={\mathit{\tau }}_{step}$$

(6)

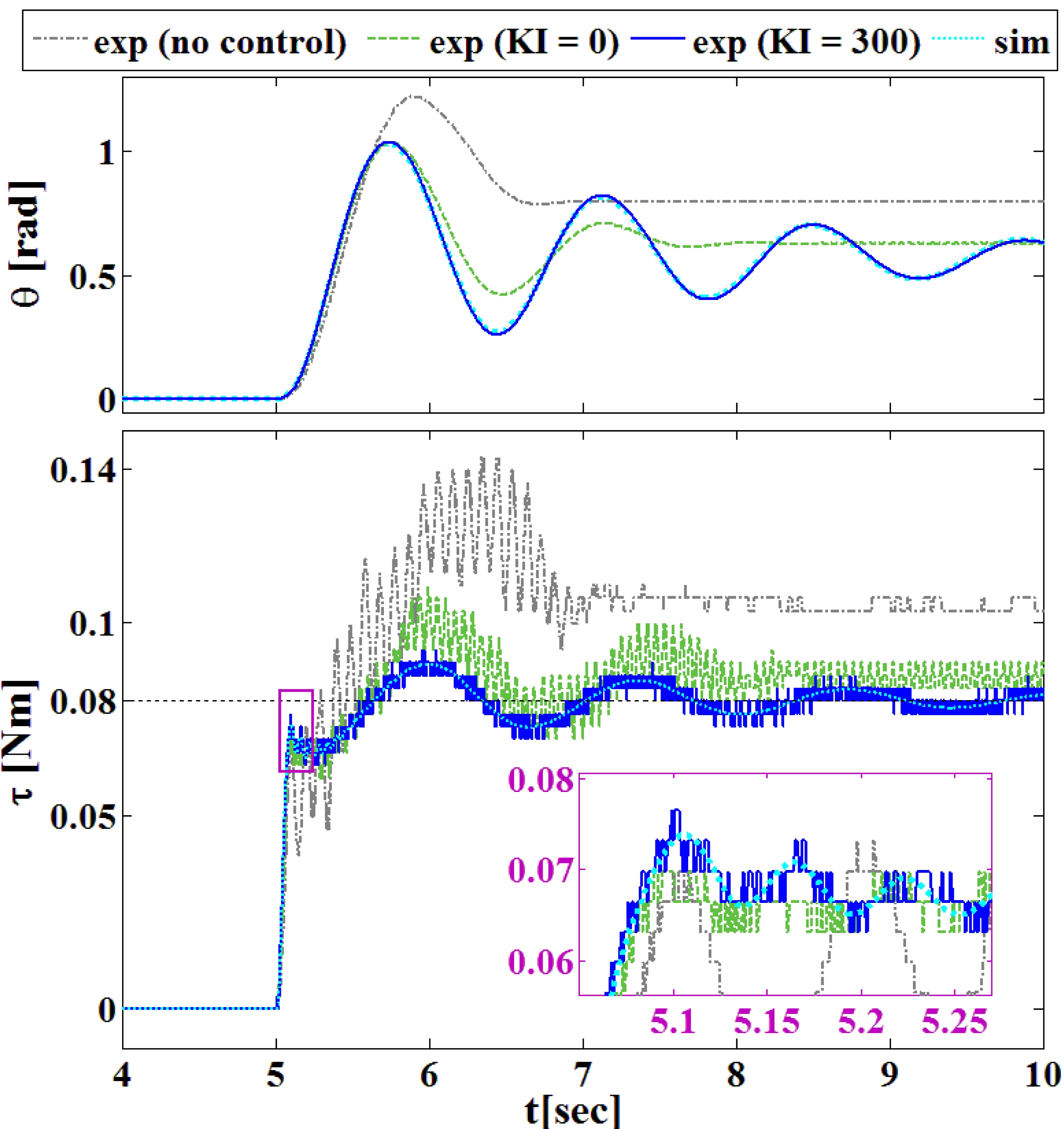
즉, 재설정된 모터 동역학은 대상시스템에 비하여 매우 작 은 점성마찰력만을 가지므로 전체 진자운동은 결국 진동 감쇠운동(under-damped motion)을 하며, 더 작은 관성모멘트 를 가지기 때문에 입력된 τ_step 을 중심으로 더 작은 관절 탄성진동(joint elastic oscillation)을 보일 것이다. 이러한 예상 된 반응은 그림 5의 시뮬레이션 그래프처럼 (6)을 이용한 시뮬레이션을 통해서 확인할 수 있다.

Fig. 5

Experimental results under gravity: θ-motor angles, τ-sensor torques

그림 5에서와 같이 θ 와 τ 를 관찰하여 모터 동역학의 변화를 확인했다. 제어기를 적용하지 않고 τ_step 을 바로 입 력을 하는 경우, 모터는 과감쇠운동(over-damped motion)을 보이고, 심한 관절탄성진동을 갖는 것을 확인할 수 있었다 (그림 5의 “no control” 참고). 대상시스템 자체가 큰 관성모 멘트를 가지고 있고 모터와 관절을 구성하는 베어링에서 고려할만한 마찰이 발생하고 있기 때문에 모터는 이런 움 직임을 보이게 된다. K_I = 0 인 IMFC를 적용하는 경우(관 절토크 피드백만 적용하는 경우), 모터 관성모멘트와 마찰 력이 동시에 줄어들게 되며, 따라서 모터는 그림 5에서와 같이 약한 진동감쇠운동을 하고, 관절탄성진동은 억제된다. 이는 ^[1]에서 제시한 연구결과와 일치한다. 그러나 이 경우 적용한 제어기의 성능은 모터 마찰력에 영향을 받기 때문 에 모터부분 동역학은 사용자가 정의한 모터 동역학을 정 확하게 추정하지는 못하게 된다. 그림 5의 실험결과에서, 모터의 움직임(녹색 선)은 사용자가 정의한 모터부분 동역 학을 바탕으로 시뮬레이션을 통해 얻은 움직임(시안색 선) 과 차이가 나는 것을 알 수 있다. 따라서 관절토크 피드백 만을 이용할 경우 모터 동역학을 원하는 대로 재설정하는 데 한계가 있음을 실험결과를 통해 확인할 수 있었다.

반면 K_I = 300 인 IMFC를 적용할 경우 모터의 움직임 은 시뮬레이션 결과와 정확하게 일치하는 것을 볼 수 있 다. 즉, 그림 5에서와 같이 모터의 거동이 사용자가 정의한 모터 동역학의 거동을 정확하게 추종한다. 적분 매니폴드 피드백을 통해 사용자가 정의한 마찰력 외의 모든 마찰력 은 완전히 보상되며, 따라서 모터는 진동감쇠운동을 하게 된다. 또한 센서토크 τ 도 마찰력에 의한 치우침(bias) 없 이 입력된 0.08N-m 를 중심으로 변하는 것을 볼 수 있다. 30%로 작아진 모터의 관성모멘트로 인해 관절탄성진동 자체도 크게 줄어든 것 역시 확인할 수 있다. 관절탄성진 동은 관절토크센서의 탄성으로 인한 모터부분의 관성모멘 트와 링크부분의 관성모멘트 사이에서의 에너지교환에 의 해 발생하므로, 모터의 관성모멘트를 더 작은 값으로 줄임 이면 모터에 저장되는 에너지 자체가 줄어들기 때문에 관 절탄성진동까지 억제하는 효과를 얻을 수 있다^[1]. 따라서 실용적인 측면에서도 IMFC는 유연관절로봇 제어에 유용 하다. 시뮬레이션 결과와의 약간의 차이는 링크부분 동역 학 모델의 불확실성과 사용한 엔코더의 분해능(resolution) 의 한계에서 기인하는 것으로 추측된다.

이와 같이 제안한 IMFC는 유연관절로봇에 추가적인 불안 정성을 야기하지 않으면서도 모터 동역학을 정확하게 재설 정할 수 있음을 실험을 통해 충분히 검증할 수 있었다.

5. 결 론

본 논문에서는 유연관절로봇의 모터 동역학을 재설정하 기 위한 강인 제어기를 제안하였다. 제안한 IMFC는 관절 토크 피드백과 사용자가 정의한 모터 동역학을 기반으로 만들어진 특별한 적분매니폴드 피드백으로 구성된다. 제안 한 제어기는 모터 외란 하에서도 정확한 모터 동역학 재 설정을 보장하며, 이론적인 증명과 실험적인 검증을 통해 성능을 확인하였다. 실험적 검증을 위하여 1자유도 유연관 절로봇을 이용하여 중력 하에서 실험을 수행하였다. 시뮬 레이션을 통해 얻은 결과와 비교를 통해 IMFC를 사용하 면 모터 동역학이 사용자가 정의한 대로 정확하게 재설정 된 것을 확인할 수 있었다. 제안한 IMFC는 유연관절로봇 제어의 성능을 높이거나, 관절토크센서로 인해 발생하는 관절탄성진동을 줄이는 데 활용할 수 있다. 감속기가 사용 된 로봇에서 감속기로 인해 증폭된 모터 관성모멘트를 줄일 수 있으면 충돌 시 충돌하중(impact load)를 줄일 수 있어 대 인 안전성(safety)을 향상시킬 수 있다^[14]. 이런 측면에서 IMFC를 안전성 향상을 위해서도 활용할 수 있을 것이다.

References

• Ott, C., Albu-Schaffer, A., Kugi, A., Hirzinger, G., “On the passivity based impedance control of flexible joint robots”, IEEE Trans. Robot, (2008, Apr), 24(2), p416-429. [https://doi.org/10.1109/tro.2008.915438]
• Chen, K.-P., Fu, L.-C., “Nonlinear adaptive motion control for a manipulator with flexible joints”, (1989), Proc. IEEE Int. Conf. on Robotics and Automation (ICRA), p1201-1206. [https://doi.org/10.1109/robot.1989.100144]
• Albu-Schaffer, A., Hirzinger, G., “State feedback controller for flexible joint robots: A globally stable approach implemented on DLR’s lightweight robots”, (2000), Proc. IEEE Int. Conf. on Intelligent Robots and Systems (IROS), p1087-1093. [https://doi.org/10.1109/iros.2000.893164]
• Park, Y.J., Lee, H., Oh, Y., Chung, W.K., “Development of Kalman filter based two-port body force observer for the flexible joint: Design and experiments”, (2012), Proc. IEEE Int. Conf. on Robotics and Automation (ICRA), p2717-2722. [https://doi.org/10.1109/icra.2012.6225384]
• Albu-Schaffer, A., Hirzinger, G., “Parameter identification and passivity based joint control for a 7 DOF torque controlled light weight robot”, (2001), in Proc. IEEE Int. Conf. on Robotics and Automation (ICRA), p2852-2858. [https://doi.org/10.1109/robot.2001.933054]
• Lee, H.S., Tomizuka, M., “Robust motion controller design for high accuracy positioning systems”, IEEE Transactions on Ind. Electron, (1996), 43(1), p48-55.
• Le Tien, L., Albu-Schaffer, A., De Luca, A., Hirzinger, G., Friction observer and compensation for control of robots with joint torque measurement, (2008), in Proc. IEEE/RSJ Int. Conf. on Intelligent Robots and Systems (IROS), p3789-3795. [https://doi.org/10.1109/iros.2008.4651049]
• Zhao, Y., Zhao, Z., Zhao, B., Li, W., “Active Disturbance Rejection Control for Manipulator Flexible Joint with Dynamic Friction and Uncertainties Compensation”, (2011), in Proc. Fourth International Symposium on Computational Intelligence and Design (ISCID), p248-251. [https://doi.org/10.1109/iscid.2011.164]
• Kaneko, K., Kondo, S. i., Ohnishi, K., A motion control of flexible joint based on velocity estimation, (1990), in Proc. 16th Annual Conf. IEEE Industrial Electronics Society (IECON'90), p279-284. [https://doi.org/10.1109/iecon.1990.149151]
• Lee, H., Oh, Y., Song, J.-B., “Torque sensor based robot arm control using disturbance observer”, (2010), in Proc. Int. Conf. on Control Automation and Systems (ICCAS), p1697-1700. [https://doi.org/10.1109/iccas.2010.5669771]
• Bang, J.S., Shim, H., Park, S.K., Seo, J.H., “Robust tracking and vibration suppression for a two-inertia system by combining backstepping approach with disturbance observer”, IEEE Tran. Ind. Electron, (2010), 57, p3197-3206. [https://doi.org/10.1109/tie.2009.2038398]
• Castaños, F., Fridman, L., “Analysis and design of integral sliding manifolds for systems with unmatched perturbations”, IEEE Trans. Autom. Control, (2006), 51(5), p853-858.
• Henein, S., Spanoudakis, P., Droz, S., Myklebust, L.I., Onillon, E., “Flexure pivot for aerospace mechanisms”, (2003), in Proc. 10th European Space Mechanisms & Tribology Symposium, p285-288.
• Zinn, M., Roth, B., Khatib, O., Salisbury, J.K., “A new actuation approach for human friendly robot design”, Int. J. Robot. Res. (IJRR), (2004), 23(4-5), p379-398. [https://doi.org/10.1177/0278364904042193]