수중로봇 위치추정을 위한 베이시안 필터 방법의 실현과 거리 측정 특성 분석

1. 서 론

수중 로봇은 심해 자원 조사, 수중 구조물 건설, 수산업, 군사적 용도 등으로 사용되어지고 있다^[1]. 이를 위해 수중 로봇의 경로 계획, 장애물 회피 기술, 위치추정 기술, 지도 작성 기술 등과 같은 로봇의 자율 주행 기술이 요구된다^[2]. 특히 위치추정 기술은 다른 요소 기술들을 실현하기 위해 필수적으로 요구되는 기술이다. 수중 위치추정을 위한 확 률 기반 방법으로는 칼만 필터(Kalman Filter: KF), 확장 칼만 필터(EKF), 무향 칼만 필터(Unscented Kalman Filter: UKF), 파티클 필터(Particle Filter: PF) 또는 MCL 방법 등이 있다. 수중 로봇의 확률 기반 위치추정 방법은 Julier^[3], Wan^[4], Gordon^[5]에 의해서 발전되어왔다.

EKF는 수중 로봇 운동의 경우와 같이 상태 천이와 측 정모델 함수가 비선형인 경우 선형화를 통하여 상태를 추 정한다. 또한 상태 천이와 측정 오차가 가우시안 분포를 가 지는 경우를 가정한다. 따라서 수중 로봇에서의 경우와 같 이 상태 천이와 측정이 비선형성을 가지며, 오차에 비 가우 시안 특성이 강한 경우 위치 추정 성능이 저하될 수 있다^[6].

파티클 필터를 이용한 위치 추정 또는 MCL 방법은 다 수의 파티클을 이용하여 로봇의 확률적 위치 분포를 나타 내며, 상태 천이와 측정에서 비선형 모델 함수를 그대로 이 용한다. 따라서 비가우시안 오차 요소가 많고, 비선형성이 큰 수중 로봇의 경우에도 일반적으로 우수한 위치 추정 성 능을 보인다. 그러나 추정해야할 변수가 많아지면 계산량 이 많아져서 실시간 적용에 부적합해지는 문제점이 있다^[7].

현재 수중 로봇 위치추정을 위해서는 GPS(Global Positioning System), DVL(Doppler Velocity Log), IMU(Inertial Measurement Unit), LBL(Long Base Line), SBL(Short Base Line), USBL(Ultra Short Base Line) 등 의 고가의 센서 시스템들이 일반적으로 사용되고 있다. 하 지만 본 연구에서는 이러한 고가의 센서 시스템들을 사용 하지 않고 로봇의 추진기(Thruster) 회전 속도, 러더 (Rudder) 각, 엘리베이터(Elevator) 각 정보와 음향 비이컨 에 의한 거리 정보를 사용하여 EKF와 MCL 방법에 의해 수중 로봇 위치 추정을 구현한다. 특히 음향 비이컨에 의한 거리 측정 값은 증명되지 않는 불확실성과 비정상 오차를 포함하고 있다. 따라서 본 논문에서는 원시 데이터 값을 사 용하는 경우와 측정된 거리 값이 비정상이라고 판단되는 경우 비정상 데이터 제거를 통한 위치 추정 결과를 비교하 였다^[8]. 또한, 수중 로봇의 위치추정 성능 향상을 위해 실험 을 통해 획득한 거리 측정 데이터를 분석하여 센서의 측정 오차를 분석하였다.

논문의 구성은 다음과 같다. 2장은 논문에서 다루는 수 중 로봇의 위치추정 조건을 기술하여 문제를 설정한다. 그 리고 이 문제를 해결하기 위한 EKF와 MCL 방법에 대해 서 설명한다. 3장은 EKF와 MCL방법의 위치 추정 성능을 실험을 통해 검증하고, 센서의 오차 특성을 분석하는 과정 을 설명한다. 마지막으로 4장에서 결론을 맺는다.

2. 수중 로봇 위치추정 방법

2.1. 문제 구성

본 논문은 그림 1과 같은 항주형(Cruising type) 수중 로봇을 대상으로 위치추정 방법을 실현한다.

Fig. 1

Cruising type underwater robot

수중 로봇은 자기수용성(Proprioceptive)정보인 추진기 회전 속도, 러더 각, 엘리베이터 각의 정보와 외부 수용성 (Exteroceptive)센서 측정 정보인 음향 비이컨으로부터의 거리 정보를 이용하여 위치를 추정한다.

본 논문에서 로봇의 위치, 방향, 속도 등은 SNAME (Society of Naval Architects and Marine Engineers)에서 정한 표준 표기법에 따라 표시한다^[9]. 로봇의 속도 정보 (u,v,w,p,q,r)중 u 가속도는 식 (1)과 같이 나타낼 수 있 다. K는 추진기 회전 속도와 서지(Surge) 속도 사이의 비 례 상수이고, t_rpm는 추진기의 분당 회전 수 이다.

$$ u=K•t_{\mathit{rpm}}$$

(1)

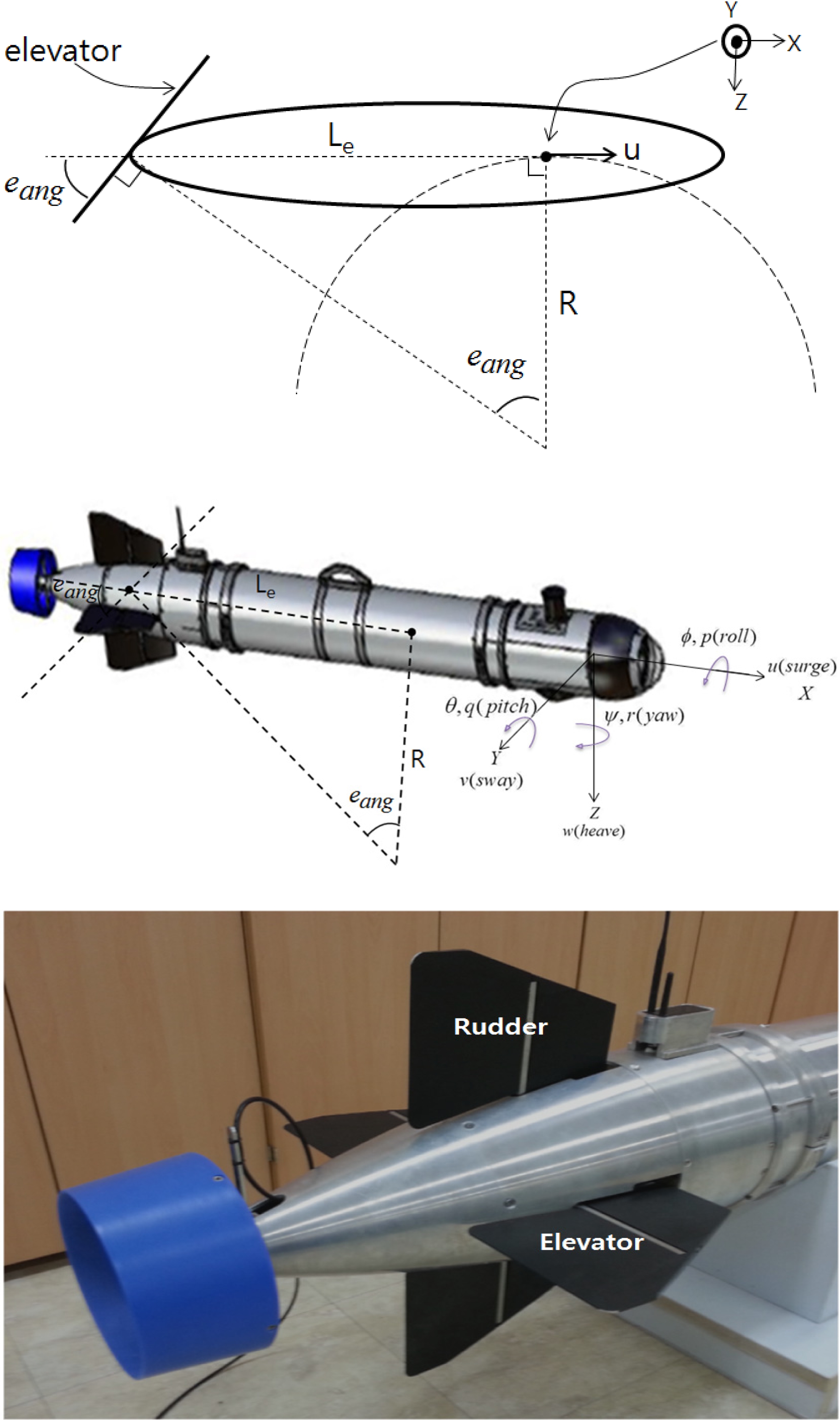
각속도 q는 그림 2를 이용하여 구할 수 있다. 그림 2에 서 다음 식 (2), (3)이 구해진다.

Fig. 2

Derivation of q

$$ \frac{L_e}{R}=tan\left(e_{\mathit{ang}}\right)$$

(2)

$$ \frac{1}{R}=\frac{q}{u}$$

(3)

식 (3)에서 식 (4)가 유도 되고, 식 (2)에서 식 (5)가 유도된다.

$$ q=u•\frac{1}{R}$$

(4)

$$ \frac{1}{R}=tan\left(e_{\mathit{ang}}\right)/L_e$$

(5)

따라서, 식 (5)를 식 (4)에 대입하여 각속도 q가 다음 식 (6)과 같이 구해진다.

$$ q=u•tan\left(e_{\mathit{ang}}\right)/L_e$$

(6)

e_ang는 엘리베이터 각, L_e은 엘리베이터와 수중 로봇 피치(Pitch) 운동의 중심점 사이의 길이를 나타낸다. L_e는 로봇의 무게 중심이 아닌 부가 질량(Added mass)까지 포 함한 가상의 위치까지의 거리로서 본 논문에서는 실험을 통하여 L_e는 3.0m로 설정하였다.

각속도 r은 q와 동일한 방법으로 식 (7)과 같이 유도된다.

$$ r=u•tan\left(r_{\mathit{ang}}\right)/L_r$$

(7)

r_ang는 러더 각, L_r 은 러더와 수중 로봇 요(Yaw) 운동의 중심점 사이의 길이를 나타낸다. 본 연구에서는 그림 1과 같은 항주형 타입의 수중 로봇을 사용하므로 v,w,p 제어 는 고려하지 않는다.

엘리베이터는 수중로봇 동작의 피치를 제어하며 러더 는 요를 제어한다. 엘리베이터와 러더의 각도를 조합하여 롤 제어도 가능하나 본 연구에서는 롤 제어는 고려하지 않 으므로 로봇의 Y축을 중심으로 회전하는 두 개의 엘리베이 터를 항상 동일한 방향과 동일한 각도로 제어한다. 그림2는 로봇의 Y축 음의 방향으로 본 측면의 그림을 사용하여 엘 리베이터 각 e_ang과 피치 각속도의 관계를 표현하였다. 그림 에서 러더와 추진기는 표시하지 않았다. 만일 엘리베이터 각 e_ang를 러더 각 r_ang로 하면, 요 각속도 r 과 r_ang사이의 관 계를 표현하게 된다.

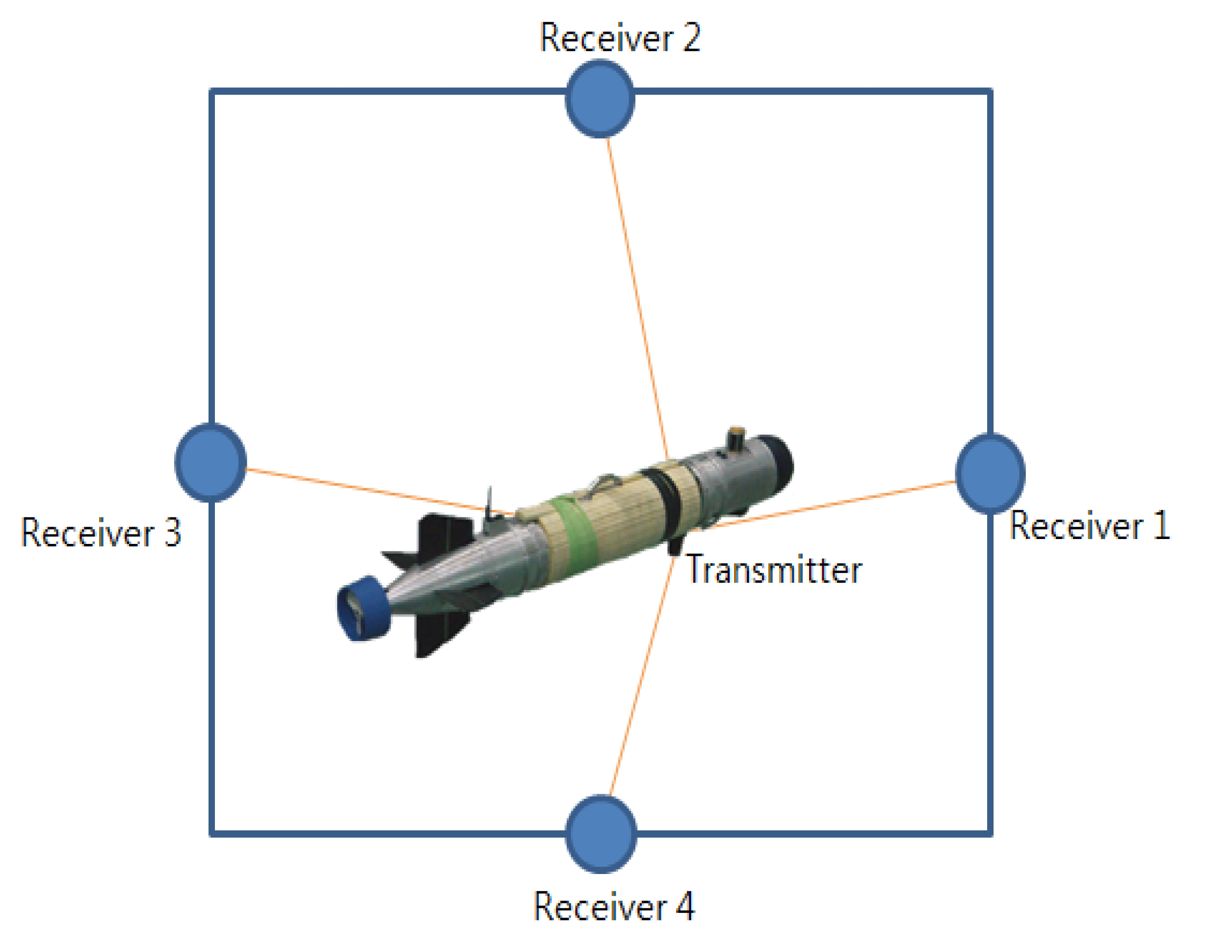
실험에서는 그림 3과 같이 4개의 비이컨에 음향 수신기 를 설치하고 수중 로봇에는 음향 신호를 송신할 수 있는 송신기를 설치하였다. 수중 로봇에서 음향 신호를 송신하 면 외부에 설치된 비이컨의 음향 수신기에서 TOA(Time Of Arrival)정보를 이용하여 EKF와 MCL에 사용하기 위 한 거리 데이터를 계산한다.

Fig. 3

Setup for experiments

2.3. MCL

MCL알고리즘은 파티클들을 이용한 확률 기반 위치추 정 방법이다. 표 1에 MCL알고리즘을 의사 코드로 나타내 었다^[11]. X_t는 M개의 파티클들의 집합으로서, 시각 t에서 의 로봇 위치의 확률적 분포를 나타내고, z_t는 음향 비이컨 에서 검출된 거리 값, u_t는 자기 수용성 정보로서 추진기 회전 속도, 러더 각, 엘리베이터 각, AHRS 센서에서 출력 된 롤, 피치, 요의 측정값이고, E는 환경에 관한 정보로서, 여기에서는 음향 비이컨의 위치 정보이다.

Table 1

Pseudo code for MCL

표 1의 3행은 추측항법(Dead-reckoning) 방법으로서 전단계의 파티클 위치로부터 현재의 파티클 위치를 예측하 는 과정이다. 4행은 예측된 파티클 위치에 대한 추정 신뢰 도를 계산하는 과정이다. 여기에서는 음향 비이컨에서 측 정된 거리 값과 해당 파티클에서 계산한 비이컨까지의 거 리 값을 비교하여 신뢰도를 계산한다. 6~8행은 파티클에 대한 신뢰도를 기반으로 파티클들을 재선별하는 과정이다. 이러한 과정이 반복될 때마다 파티클들의 분포가 추정된 로봇의 위치를 나타낸다.

2.3.1. 모션모델

수중 로봇에 대한 모션 모델은 수중 로봇의 자기 수용 성 정보 (u,v,w,p,q,r) 를 사용하여 파티클들의 위치를 예측 한다. 표 2는 본 연구에서 사용한 모션 모델을 나타낸다. 여기에서 α 파라미터 α_uu~α_rs는 (u,v,w,p,q,r)에 포함된 속도 불확실성을 고려할 수 있게 한다. 자기 수용성 정보 (u,v,w,p,q,r)에 오차가 큰 경우에는 해당되는 α 파라미터 를 크게 설정하여야 한다^[12]. 즉, α_uu~α_rs 에 의해서 자기 수용성 속도 정보의 불확실성을 고려하여 u∧,v∧,w∧,p∧,q∧,r∧를 구한다. T_E1,T_E2는 로봇 좌표계에서 표현된 속도를 지 구 고정 좌표계에서의 속도로 변환해주는 행렬이다^[13]. T_E1 은 로봇의 선속도, T_E2는 로봇의 각속도에 대한 변환 행렬 이다. sample() 함수는 오차 범위 내에서 하나의 값을 선 택해주는 함수이다. motion model()은 속도의 불확실성 을 고려하여 로봇의 위치를 (x′,y′,z′,Φ′,θ′,ψ′) 로 예측하 여준다.

Table 2

Motion model used in MCL

2.3.2. 센서모델

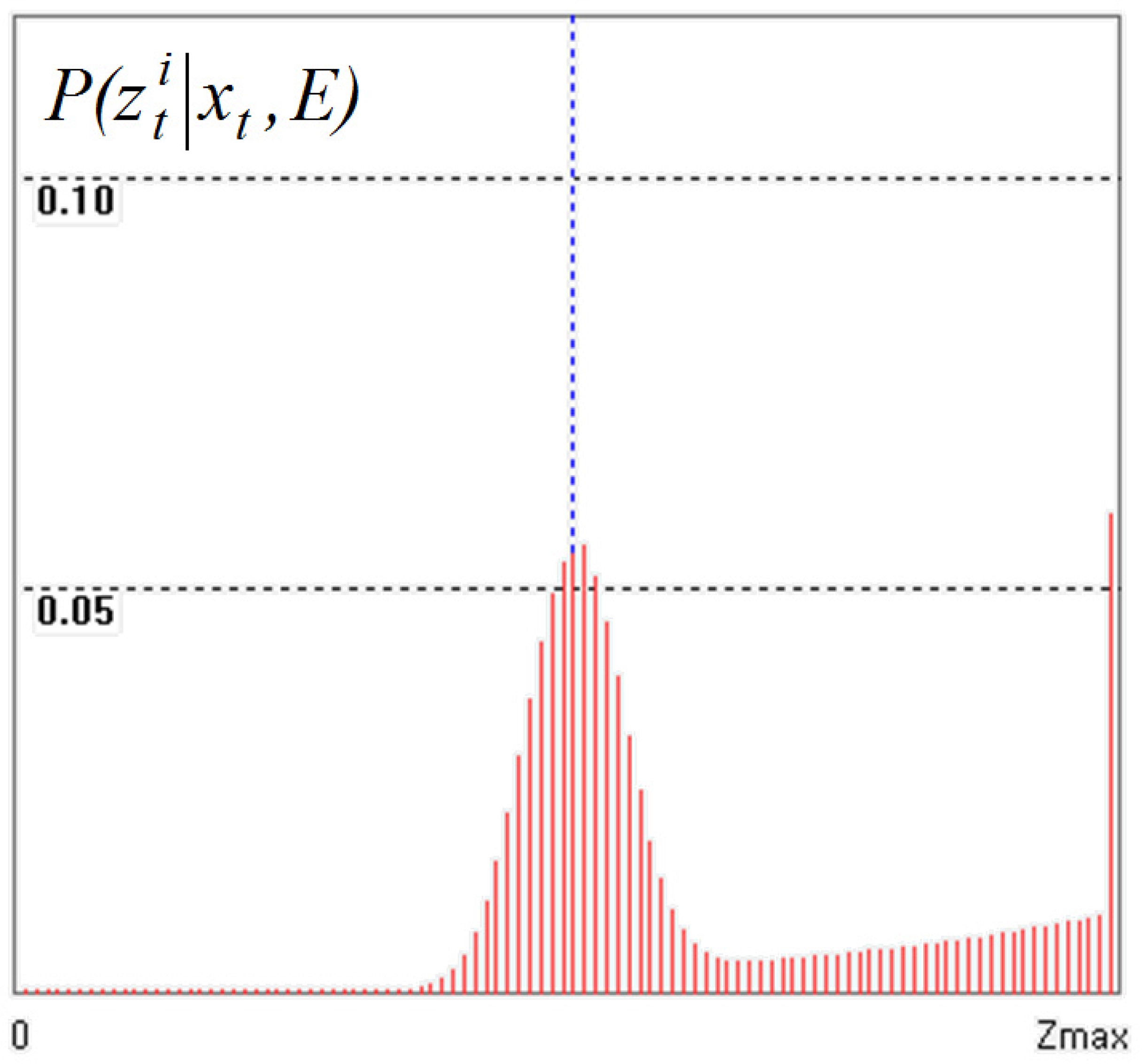
센서 모델은 외수용성 센서에 의해 측정된 데이터 zti와 파티클에서 계산된 센서 데이터를 비교하여 파티클에 대한 신뢰도를 부여한다. 신뢰도는 4개의 확률 분포 요소 Phitztixt,E,Plongztixt,E,Pmaxztixt,E, 그리고 Prandztixt,E를 조합하여 구한다^[14,15]. Phitztixt,E는 센서 측정 정보에 가우시안 특성을 가지는 잡음이 포함되 어있음을 고려한다. Plongztixt,E은 동적 또는 정적 장애 물이 로봇과 비이컨 사이에 있는 경우를 고려한 확률 분포 이다. Pmaxztixt,E는 센서 정보가 수신되지 않거나, 동작 하지 않는 상황에서의 센서 감지 실패를 나타내주는 확률 분포이다. Prandztixt,E는 센서 정보가 설명 불가능한 측 정 오차를 가지는 경우를 나타내는 확률분포이다. zti는 센 서에 의해 측정된 로봇과 i번째 비이컨 사이의 거리 정보, x_t는 예측된 파티클의 위치, E는 환경 정보이다. 식 (14)는 4개의 확률 분포 요소들을 가중치 S_hit, S_long, S_max, S_rand에 의해 조합하여 신뢰도를 계산하는 함수이다. 그림 4는 4개의 확률 분포 요소들을 나타낸 추정 가중치 확률 분포 도이다.

Fig. 4

Probability distribution for the sensor model

확률분포 요소 P_max에서 Z_max는 음향 비이컨에서 로봇까 지의 거리 정보가 센서 동작상의 오류에 의해서 측정되지 않는 경우에 센서로부터 출력되는 거리를 의미한다. 본 연 구에서 사용된 음향 센서의 경우 비이컨에서 음향 신호 발 생에 문제가 발생하거나 거울반사(Specular reflection), 신 호 간섭, 각종 요인에 의한 비정상적인 신호 감쇠 또는 수 신부에서 입력 신호를 판별하지 못하는 경우에 거리 값이 Z_max로 출력된다. 이러한 센서의 정상 동작 실패 현상을 설 명하는 확률분포 성분이 P_max이다.

$$ \begin{array}{c}P\left(z_t^i\left|x_t,E\right.\right)={\left(\begin{array}{c}{S}_{\mathit{hit}}\\ S_{\mathit{long}}\\ S_{max}\\ S_{\mathit{rand}}\end{array}\right)}^T•\left(\begin{array}{c}{P}_{\mathit{hit}}\left(z_t^i\left|x_t,E\right.\right)\\ P_{\mathit{long}}\left(z_t^i\left|x_t,E\right.\right)\\ P_{max}\left(z_t^i\left|x_t,E\right.\right)\\ P_{\mathit{rand}}\left(z_t^i\left|x_t,E\right.\right)\end{array}\right)\\ S_{\mathit{hit}}+S_{\mathit{long}}+S_{max}+S_{\mathit{rand}}=1\end{array}$$

(14)

3. 실험 및 고찰

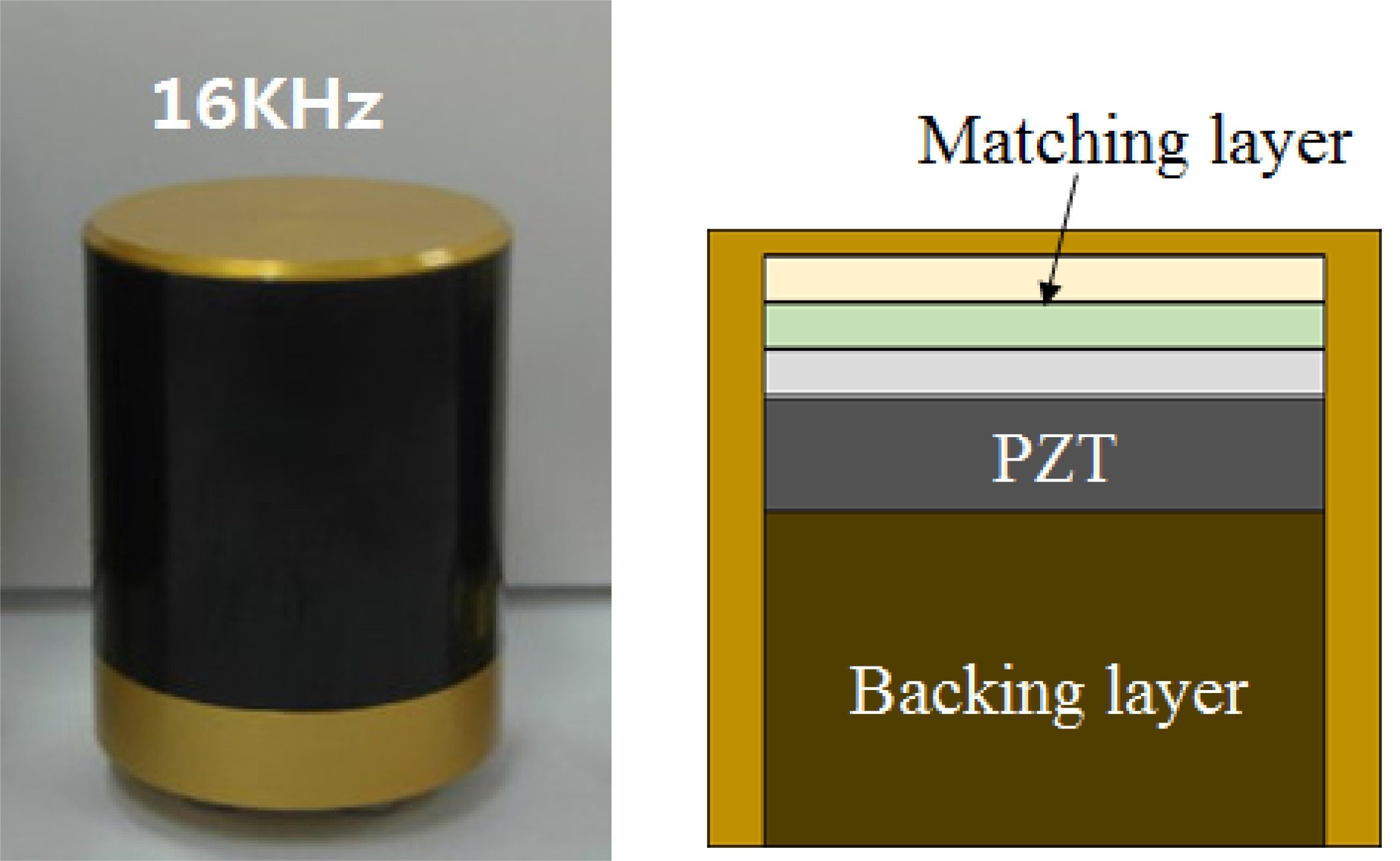
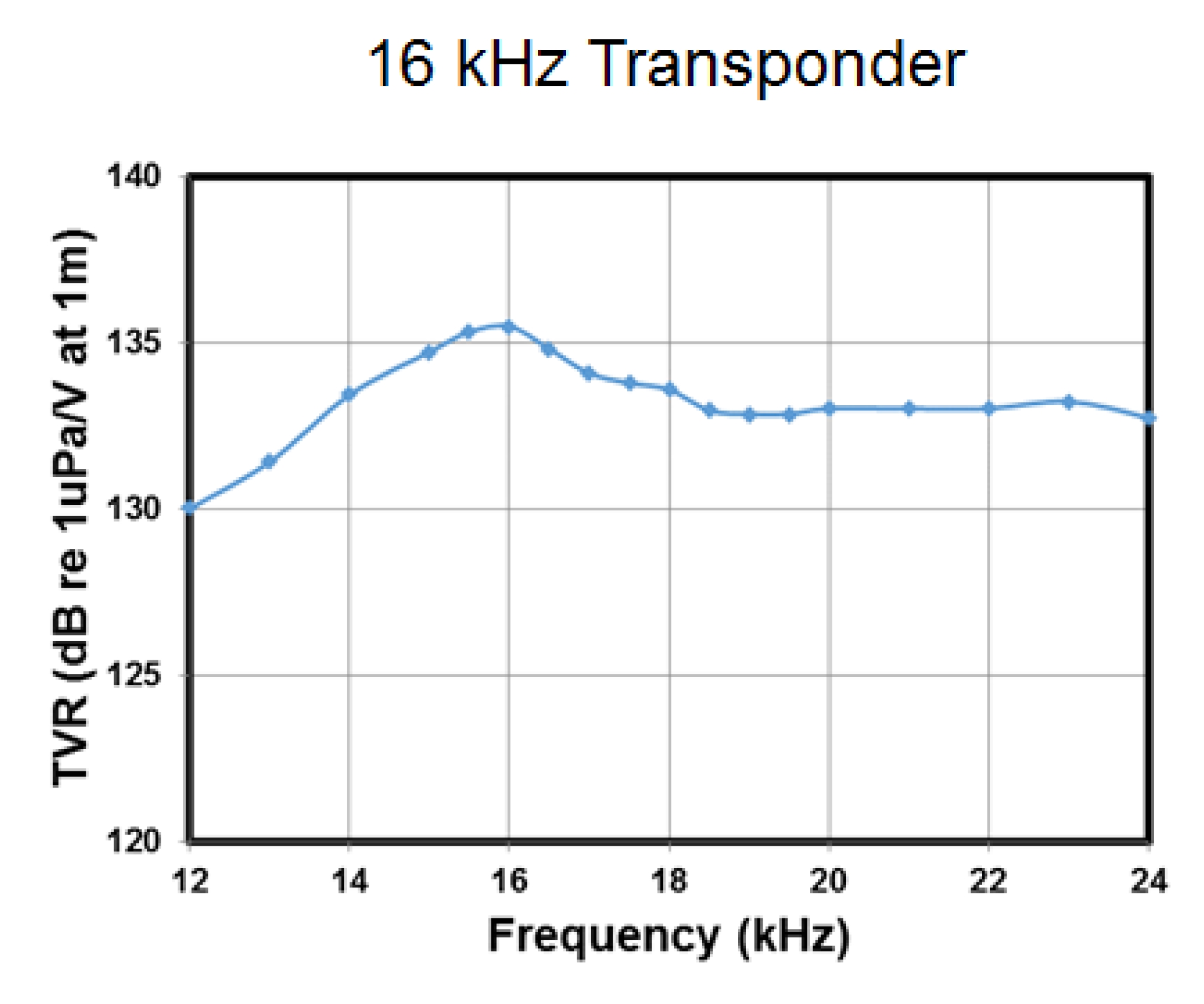
본 실험에서 사용한 로봇의 자기수용성(Proprioceptive) 정보는 추진기 회전 속도, 러더 각, 엘리베이터 각 정보이 다. 또한 로봇에 장착된 음향 송신기로부터 4개의 비이컨에 장착된 음향 수신기까지의 거리를 외부 수용성 (Exteroceptive) 센서 측정 정보로 그림 5에 나타난 16kHz 출력 특성을 가진 음향 신호 송신 센서를 사용하였다. 음향 거리 센서는 레드원테크놀러지(주)에서 개발된 시작품으로 서 아직 거리 출력 값에 대한 불확실성 특성이 구해지지 않는 단계여서 본 연구에서 불확실성 특성을 추정하였다. 그림 6은 사용된 센서의 송신전압감도(TVR) 특성을 나타 낸다. 표 3은 위치추정을 위해 이용한 추진기, 엘리베이터, 러더 엑츄에이터와 음향 거리 센서의 사양을 나타내었다.

Fig. 5

Transducer used for experiment

Fig. 6

TVR of the Transducer used for experiment

Table 3

Specification of actuators and sensors

3.1. 위치추정 실험

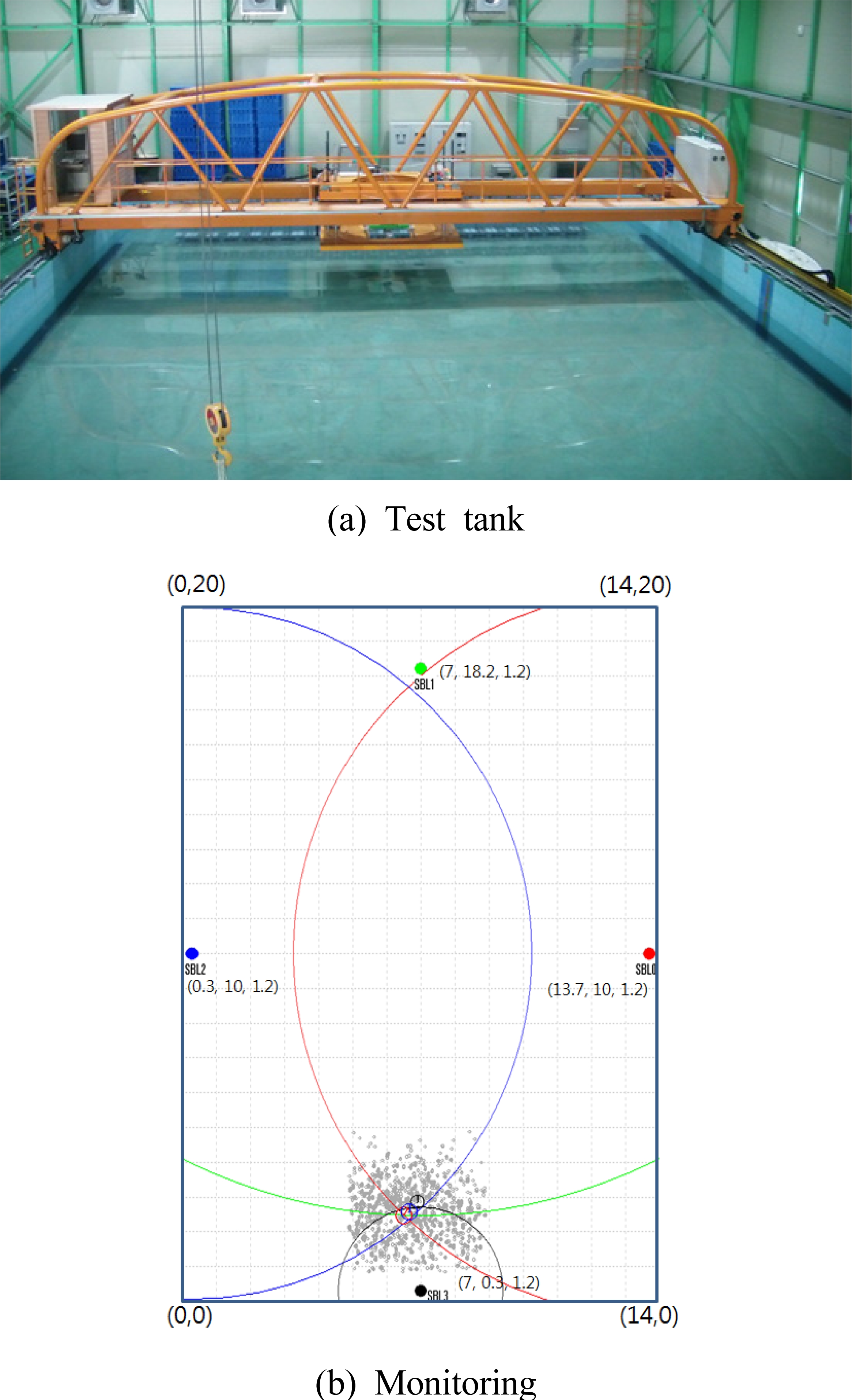
본 실험에서는 4개의 수신기와 수중 로봇에 장착된 1개 의 송신기를 이용하여 EKF, MCL에 의해 위치를 추정하였 다. 그림 7 (a)는 창원 대학교 수조 실험동 실험환경이고 (b)는 거리 정보와 위치추정 모니터링의 예를 나타내었다.

Fig. 7

Environment for experiment

음향 비이컨 4개의 수신기 위치 (x,y,z)는 그림 (b)에 나타내었고, 그림에서 각 격자의 간격은 1m이다. 그림에서 거리를 나타내는 4 개의 원호가 하단 중앙부에서 서로 근 접하며, 로봇의 위치를 나타내는 파티클들이 이 부분에 분 포되어 나타나고 있다.

위치추정 실험은 총 4가지 형태의 주행 패턴으로 진행 하였다. 다수의 시행 착오 실험을 통해 EKF와 MCL의 적 용을 위한 매개변수를 표 4와 같이 설정하였다.

Table 4

Parameter used for implementation of EKF localization and MCL

α_uu,α_ur,α_ru,α_rr는 2.3.1절에서 나타낸 모션의 불확실 성을 나타내는 α 파라미터이고 σ_r 은 거리 측정 오차의 표 준 편차이다. S_hit, S_long, S_max, S_rand은 MCL 방법 센서 모 델의 확률 분포 요소들의 가중치를 나타낸다.

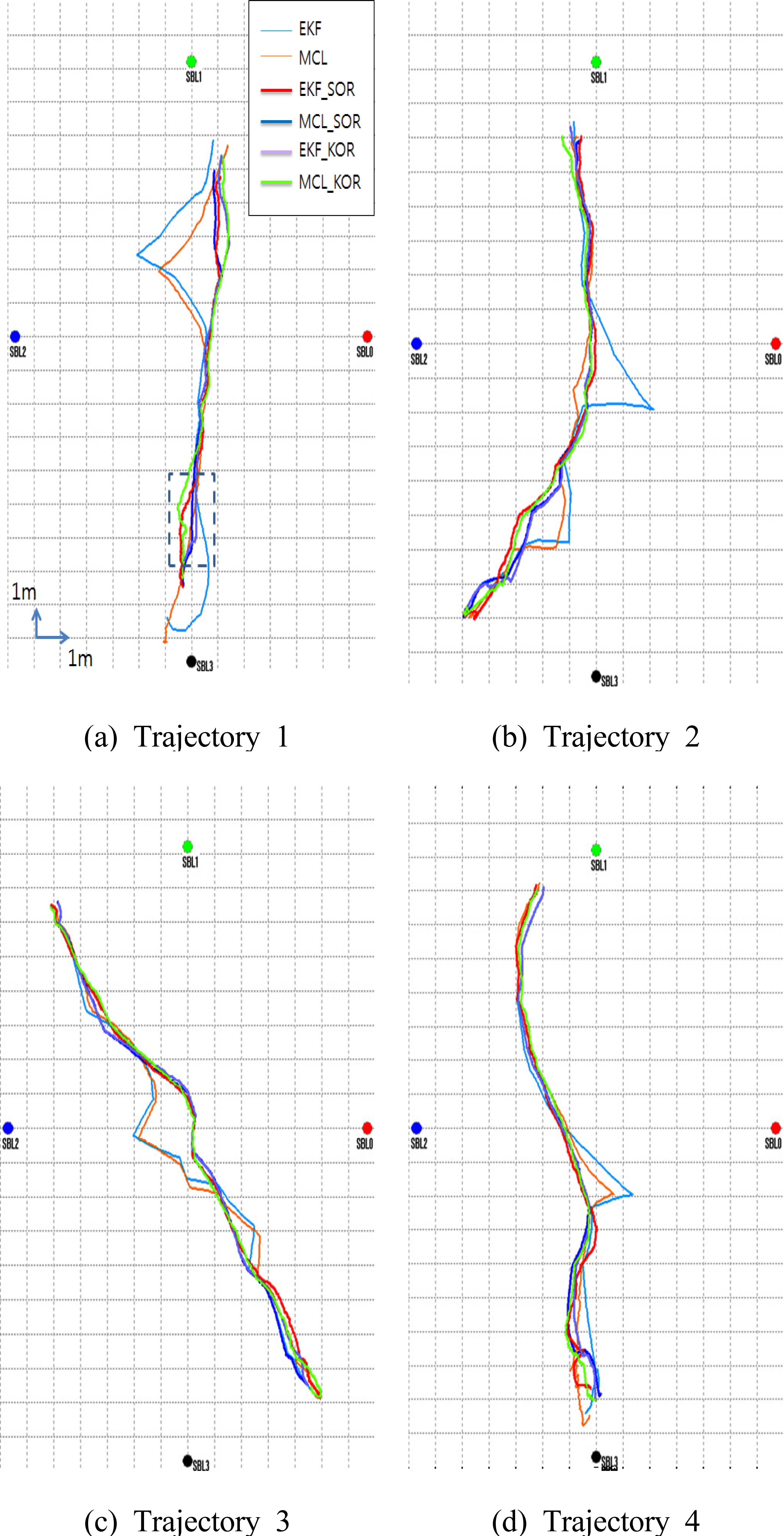
그림 8은 4가지 주행 실험을 통해 획득한 위치추정 궤 적이다. EKF, MCL은 음향 비이컨에서 측정된 4개의 거리 데이터를 비정상 여부에 관계없이 이용한 경우의 위치추정 궤적이다. EKF_SOR, MCL_SOR은 측정된 거리 값이 비 정상이라고 판단될 때 비정상 데이터를 제거한 후 EKF와 MCL을 적용한 경우의 위치추정 궤적이다. 비정상 데이터 는 센서에서 측정된 거리 값과 추정된 로봇 위치에서 계산 된 거리 값의 차이가 주어진 임계값(threshold)을 벗어난 데이터로서, 식 (15)의 조건에 해당되는 경우 비정상 데이 터로 판정하였다. 식 (15)의 z_bi 는 i번째 비이컨에서 측정된 거리 값이고 z∧ti는 추정된 로봇 위치에서 계산된 i번째 비 이컨까지의 거리 값이다. l은 비정상 거리 값으로 판단하기 위한 거리 오차의 임계값이다. 본 실험에서는 임계값을 1.5m 로 설정하였다. 이 값은 3.2 절에서 설명하는 바와 같 이 센서의 거리 오차 평균값이 최대 0.5158m이고, 표준 편 차의 최대 값이 0.9515m임을 고려하여 설정하였다.

Fig. 8

Estimated robot navigation trajectory

$$ ‖z_{\mathit{bi}}-{\stackrel{\wedge }{z}}_{\mathit{ti}}‖\ge l$$

(15)

또한 확률기반 카이제곱 테스트(Chi-square test)를 이 용하여 비정상 데이터를 제거하여 위치추정을 실험하였다. 카이 제곱 테스트는 데이터 사이의 연관 정도를 판단하기 위한 방법이어서, 측정된 거리 정보가 어느 정도 정상적인 값으로 간주될 수 있는지 판단할 수 있는 근거를 제시해 줄 수 있다. 식 (16)에서 z∧bi는 계산된 거리 값으로서 로봇 의 위치가 정확히 추정되었다는 가정 하에 계산된다. 즉, z∧bi거리의 예상 값(Expected value)이다. 측정된 거리 오차 가 정상 분포를 가지는 것으로 가정하여 측정값과 예상 값 의 차이가 일정한 범위이내이면 정상적인 거리 데이터로 판정한다.

$$ d_i^2=\frac{{\left(z_{\mathit{bi}}-{\stackrel{\wedge }{z}}_{\mathit{bi}}\right)}^2}{{\mathit{\sigma }}_{\mathit{bi}}^2}$$

(16)

z∧bi = 로봇과 i번째 비이컨 사이의 계산된 거리값 + i번째 측정 거리 오차의 평균값

σ_bi = i번째 측정 거리 오차의 표준 편차

본 연구에서는 C=3.84로 하여 오차의 제곱이 분산 값 의 3.84배 이내이면 정상적인 거리 값으로 판정하였다. 이 경우, α=0.95 즉 측정된 데이터 중 95%는 정상으로 판정 하고 5%를 비정상 측정값으로 판정하게 된다.

EKF_COL, MCL_COL은 카이 제곱 테스트를 이용한 주행 궤적이다. 그림 8의 4개의 주행 모드에서 원시 음향 거리 데이터를 사용한 EKF, MCL 방법은 이동궤적이 정상 궤적으로부터 벗어나는 현상이 발생하였다. 그러나 EKF_SOR, MCL_SOR의 경우와 EKF_COR, MCL_COR 에서는 비정상 거리 측정 데이터의 영향이 줄어들어 추정 된 궤적이 EKF, MCL 방법보다 유연하고, 실제 로봇 궤적 을 더 잘 따라감을 실험에서 관찰할 수 있었다. 그림 9는 주행 테스트 그림 8 (a)의 사각형 점선 구역을 확대한 그림 이다.

Fig. 9

Enlarged trajectory 1

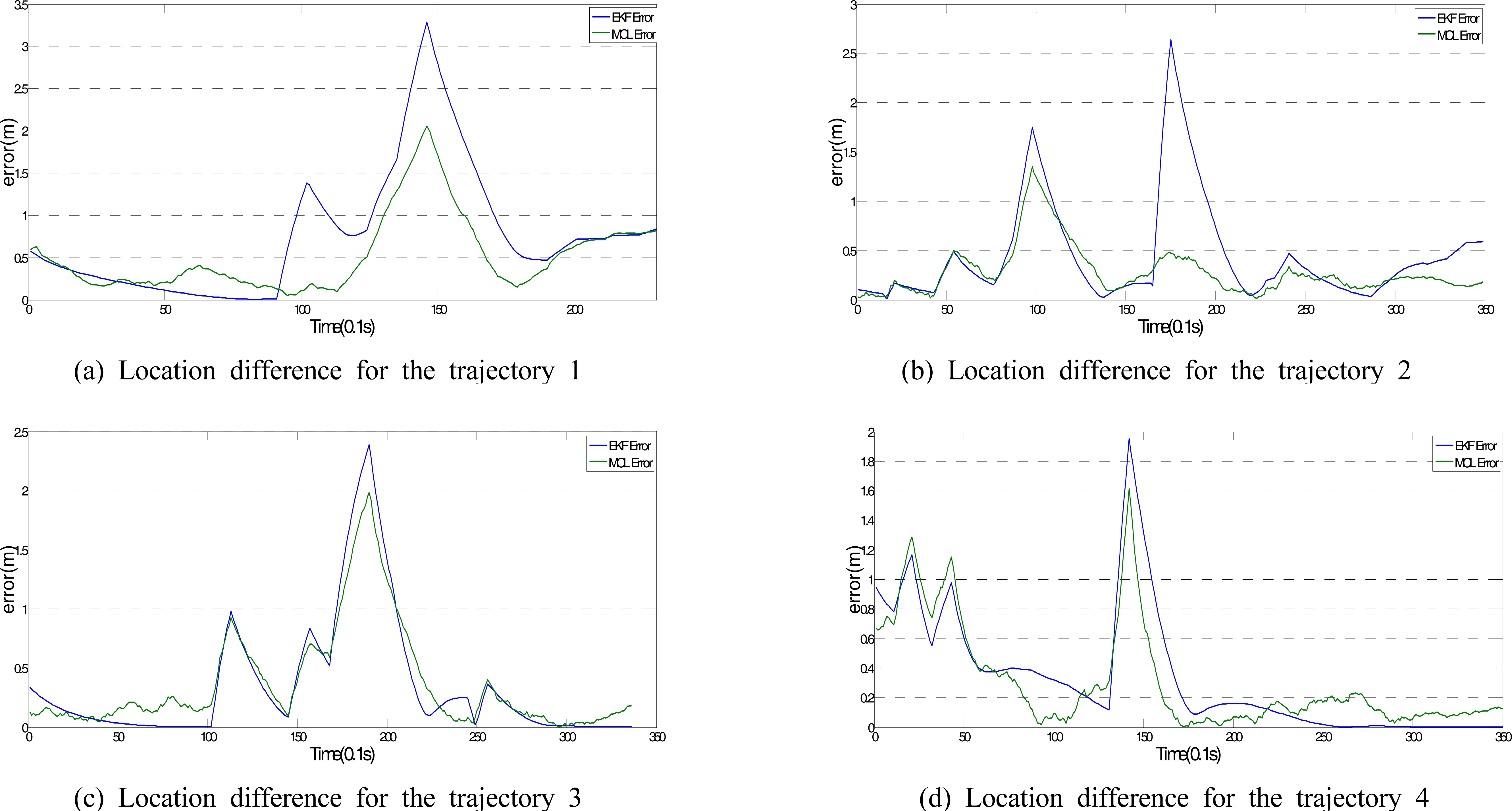
그림 8에서 나타낸 4가지 주행 테스트에 대해서 그림 10은 비정상 거리 데이터를 제거 했을 경우와 원시 거리 데이터를 사용했을 경우의 이동 궤적간의 차이를 나타내었 다. 표 5는 그림 8에서 나타난 이동 궤적의 차이를 분석하 였다. 그림 10과 표 5에서 알 수 있듯이 MCL 알고리즘은 EKF보다 비정상 거리 정보에 대해서 보다 강건함을 알 수 가 있다.

Fig. 10

Location difference of EKF and MCL without outlier rejection

Table 5

Location difference analysis for EKF and MCL without outlier rejection

3.2. 센서 오차분석

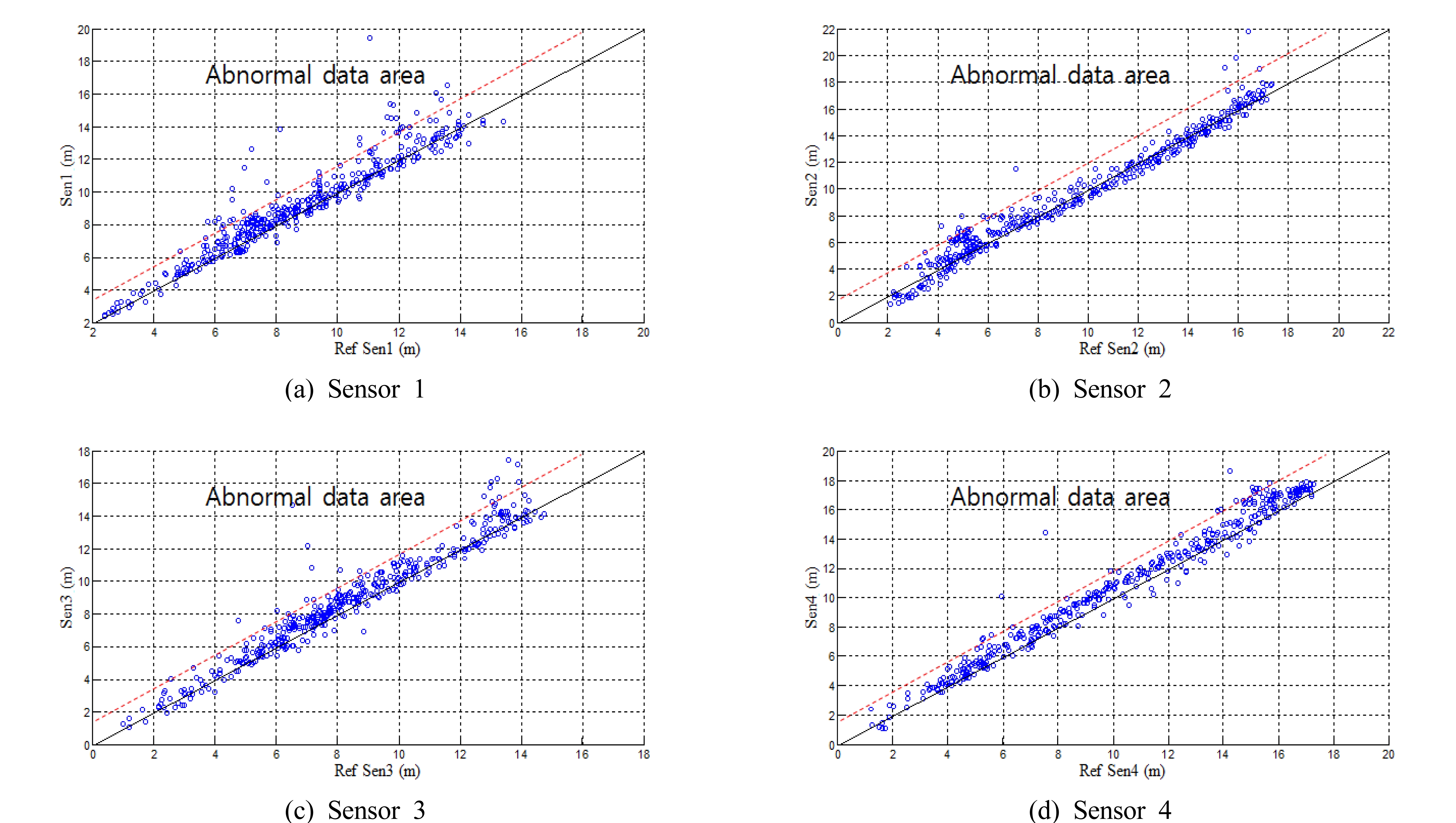
본 절은 위치추정 실험을 통해 획득한 거리 데이터의 거리 오차를 분석한다. 거리 오차의 분석을 통해 음향 거리 센서의 오차 정도를 구하였다. 그림 11은 4개의 비이컨 음 향 거리 센서에 대하여 각각 425개의 실제 측정된 거리 값 을 정상 데이터와 비교하여 나타내었다. 그림 11에서는 비 정상 데이터를 제거하고 MCL에서 구해진 추정 위치로부 터 비이컨까지의 거리를 정상(기준) 값으로 간주하였다. 실 제 센서에 의해서 측정된 거리 값이 기준 값으로부터 얼마 만큼의 오차를 가지는지 분석하였다. 그림 11 (a)~(d)를 보 면 기준 데이터 주변으로 센서 측정 거리 값이 분포되어 있지만 때때로 비정상 거리 데이터가 발생하는 현상을 볼 수 있다.

Fig. 11

Measured range data

그림 11에서 가로 축은 기준 데이터, 세로 축은 측정된 데이터이다. 이상적인 측정 데이터인 경우 기준 데이터와 일치하여야 하므로 기울기 1인 실선과 일치하여야 하나 실 제 데이터는 실선과 일치하지 않음을 알 수 있다. 빨간색 점선은 기준 데이터로부터 1.5m 떨어진 거리를 나타내며, 본 연구에서는 이 점선을 벗어난 데이터를 비정상 데이터 로 간주하였다.

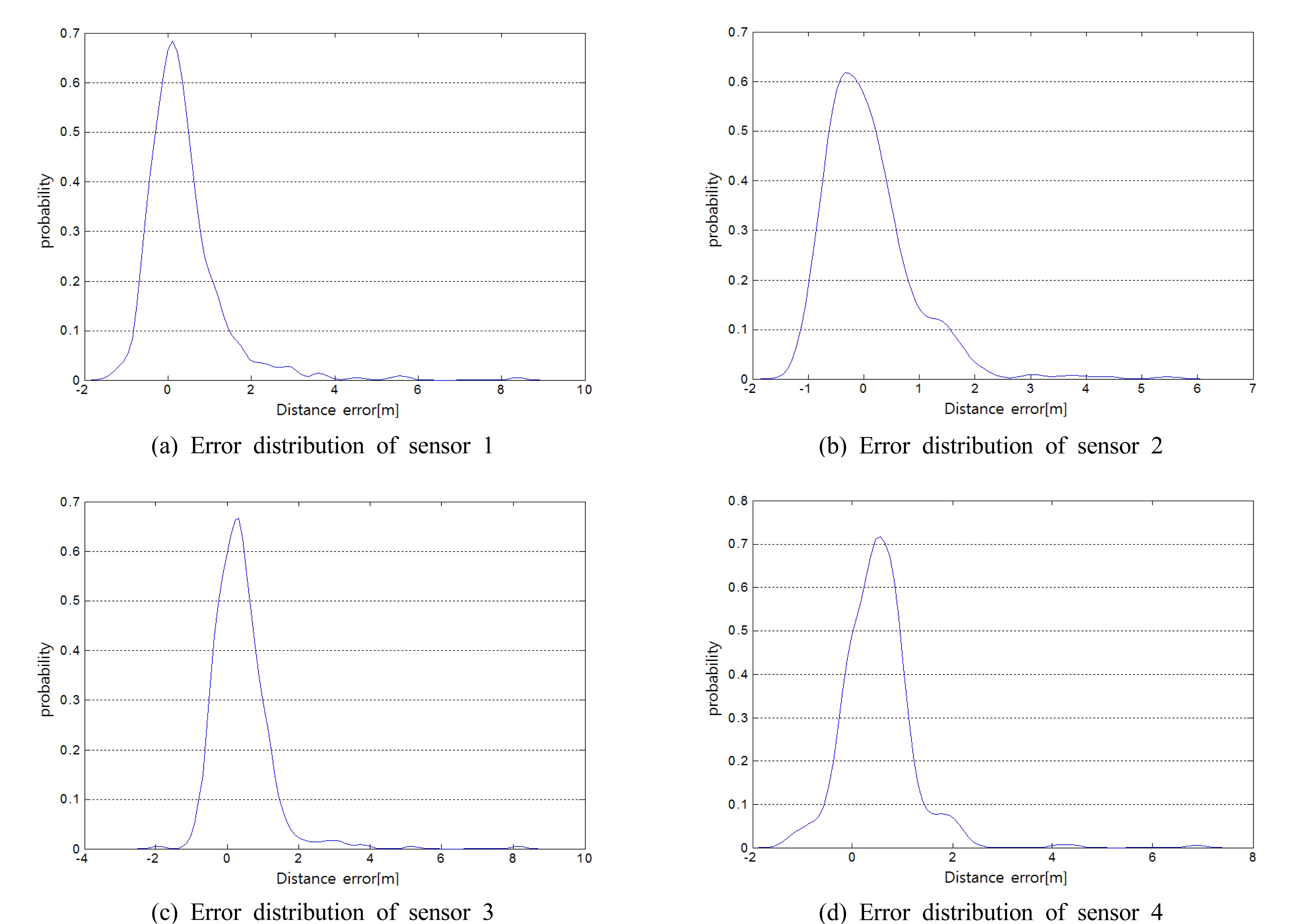
그림 12 (a)~(d)는 4개의 센서 측정 거리 오차의 확률 분포를 나타낸다. 표 6은 4개의 센서 측정 거리 오차의 평 균과 표준 편차를 나타내었다. 4개의 센서는 오차의 표준편 차가 최소 0.7213m, 최대 0.9515m가 되며, 오차의 최대 평균값은 0.5158m로 구해졌다.

Fig. 12

Range error distribution of the 4 range

Table 6

Mean and standard deviation of the range measurement error

4. 결 론

본 논문은 수중 로봇 위치추정에 EKF와 MCL 알고리 즘을 적용한 예를 보이고 성능을 분석하였다. 고가의 정밀 센서인 DVL, IMU, LBL, SBL, USBL을 사용하지 않고, 정확도가 높지 않은 음향 거리 센서 정보, 그리고 자기수용 성 정보인 추진기 회전 속도, 러더 각, 엘리베이터 각 만을 사용하여도 MCL 이나 EKF 에 의해 로봇의 위치를 추정 하는 것이 가능함을 보였다. 또한 실험을 통하여 거리 정보 를 구하는데 사용한 음향 거리 센서의 오차 특성을 분석하 였다. 구해진 거리 오차 특성 정보를 바탕으로 비정상 측정 데이터를 검출하고 이를 위치 추정 알고리즘에서 사용하지 않도록하여 추정 성능을 향상시킬 수 있음을 보였다. 본 연 구에서도 일반적으로 알려진 바와 같이 MCL이 EKF 보다 위치 추정 성능은 우수한 것으로 나타났다. 본 연구에서는 자기 수용성 정보와 4 개의 거리 정보만을 사용하여 EKF 와 MCL을 구현하였다.

향후계획은 AHRS(Attitude and heading reference system, 자세 방위 장치) 등 좀 더 다양한 센서와 수중 영상 분석을 통한 특징점 정보 등을 추가하여 사용한다면 위치 추정 성능을 더욱 향상시킬 수 있을 것으로 기대된다. 또한 실제 수중 로봇의 정확한 위치를 알 수 있는 방법을 고안하 여 위치추정 방법의 성능 분석을 정확히 할 수 있도록 실험 할 예정이다.

References

• Williams, S.B., , “Monitoring of Benthic Reference Sites Using an Autonomous Underwater Vehicle”, IEEE Robotics & Automation Magazine, (2012, Mar), 19(1), p73-84. [https://doi.org/10.1109/mra.2011.2181772]
• Borenstein, J., Everett, B., Fen, L., Navigating Mobile Robots: Sensors and Techniques, (1996), AK Peters.
• Julier, S., Uhlmann, J., Durrant-Whyte, H.F., A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators, IEEE Trans. on Automatic Control, (2000, Mar), 45(3), p477-482. [https://doi.org/10.1109/9.847726]
• van der Merwe, R., “Sigma-point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models”, Ph.D. thesis, Oregon Health & Science University, (2004, Apr).
• Gordon, N., Salmond, D., Smith, A., “Novel Approach to Nonlinear/Non-Gaussian Bayesian State Estimation”, IEEE Proc. Radar and Signal Processing, (1993), 140(2), p107-113. [https://doi.org/10.1049/ip-f-2.1993.0015]
• Lee, D.H., Yang, Y.M., Huh, K.M., “Position Estimation of MBK system for non-Gaussian Underwater Sensor Networks”, Journal of The Institute of Electronics Engineers of Korea, (2013), 50(1), p232-238. [https://doi.org/10.5573/ieek.2013.50.1.232]
• Kim, D.H., “Rao-Blackwellized Multiple Model Particle Filter Data Fusion algorithm”, The Journal of Korea Navigation Institute, (2011), 15(4), p556-561.
• Black, M.J., Rangarajan, A., “On the unification of line processes, outlier rejection, and robust statistics with applications in early vision”, International Journal of Computer Vision, (1996), 19(1), p57-91. [https://doi.org/10.1007/bf00131148]
• Society of Naval Architects and Marine Engineers, “Nomenclature for Treating the Motion of a Submerged Body through Fluid”, SNAME Technical and Research Bulletin, No.1–5, (1952, Apr).
• Fox, V., Hightower, J., Lin, L., Schulz, D., Borriello, G., “Bayesian Filtering for Location Estimation”, IEEE Pervasive Computing, (2003), 2(3), p24-33.
• Thrun, S., Burgard, W., Fox, D., Probabilistic Robotics, (2005), MIT Press.
• Kim, T.G., Ko, N.Y., Noh, S.W., Lee, Y.P., “Localization on an Underwater Robot Using Monte Carlo Localization Algorithm”, The Journal of the Korean institute of electronic communication sciences, (2011), 6(2), p288-295.
• Kang, C.W., Yoo, Y.M., Park, C.G., “Performance Improvement of Attitude Estimation Using Modified Euler Angle Based Kalman Filter”, Journal of Institute of Control, Robotics and Systems, (2008), 14(9), p1-5.
• Kim, T.G., “Localization Method for Navigation of an Underwater Robot”, Ph. D. diss., Chosun University, (2013).
• Kim, T.G., Ko, N.Y., Noh, S.W., “Simultaneous Estimation of Landmark Location and Robot Pose Using Particle Filter Method”, International Journal of Fuzzy Logic and Intelligent Systems, (2012), 22(3), p353-360. [https://doi.org/10.5391/jkiis.2012.22.3.353]