최소 제어 인자 도출을 통한 사용편의성 높은 제어시스템 설계

1. 서 론

대표적인 구동기인 전기 모터는 로봇 제작에 있어 필수 적인 요소이다. 주로 이동로봇의 바퀴를 구동하기 위해서 사용하거나, 로봇 팔의 관절을 구성하는데 사용된다. 이 때 로봇에서 어떤 목적으로 사용하느냐에 따라서 모터의 선정과 제어 방법은 달라진다^[1,2].

예를 들어 이동로봇의 바퀴 역할을 위해 사용되는 모터 는 정확한 위치 제어보다는 일정한 속도를 유지하기 위한 속도 제어 성능이 더 중요하며, 모터의 선정 시에도 정격 RPM과 공칭 토크(Nominal torque)가 무엇보다 중요하다^[3]. 반면 로봇 팔에 사용되는 모터의 경우 정확한 위치 제어 가 중요하며, 빠른 가속, 감속 및 하중 변화에 대응하기 위 해 정지 토크(Stall torque), 최대 토크(Maximum torque), 토크 상수(Torque constant) 등이 주요 선정 인자가 된다^[4]. 또한 로봇 팔에 사용되는 모터라고 할 지라도 어느 부위에 사 용되느냐에 따라서 모터의 선정은 달라져야 한다. 인간형 팔의 어깨관절과 손목관절에 사용되는 관절, 각 관절 중에 서도 피치 각(Pitch)을 구동하는 모터와 롤 각(Roll)을 구동 하는 모터는 각각 다른 성능이 요구된다.

이처럼 같은 모터라 할지라도 사용 용도에 따라서 다양 한 성능이 요구되며, 이를 위한 제어 역시 모터가 사용되 는 환경에 따라서 적합하게 이루어져야 한다. 제어 분야 전문가라면 각각의 조건에 맞게 최적 성능의 제어기 설계 를 통해서 목적을 달성할 수도 있지만, 로봇 설계자 또는 개발자의 경우 모든 경우에 대해 적합한 제어기 설계를 한다는 것은 쉬운 일이 아니다.

이동로봇의 바퀴에 사용되는 바퀴구동 모터는 속도 제 어가 필요하고, 로봇 팔 관절에 사용되는 관절구동 모터의 경우에는 토크 제어 또는 위치 제어가 요구된다. 여기에 더해 이러한 모션 제어는 하중의 변화와 같은 주변 환경 변화에 자주 노출되기 쉬우며 이에 대한 강인 제어기는 설계가 복잡하고 운용하기가 쉽지 않다. 바퀴 구동 모터의 경우 적재하중을 고려하여 기구부의 무게에 대한 보상이 필요하며 외란(disturbance)과 모델링 오차 등에 강인한 속 도 제어기가 필요하다. 로봇 팔 구동모터 또한 무게변화에 강인한 제어 성능이 필요하다.

또한 제어기 운용 시 가장 어려운 부분 중 하나는 제어 성능을 확보하기 위한 제어 인자(parameter)의 정밀조정 작 업이다. 기계시스템의 변경이나 모터의 변경으로 인하여 모델링 인자가 바뀌는 경우, 하중의 변화가 자주 발생하거 나 외란의 영향이 증가할 경우 변경된 환경에 맞게 제어 기의 인자를 조정해야 하는 경우가 생긴다. 그러나 제어기 에 익숙하지 않은 사용자일 경우 이러한 복잡한 시스템 인자를 적절하게 선정하고 제어 이득(control gain) 값 조절 등 시스템에 영향을 미치는 요소들을 결정짓는 것에 힘들 어 하는 경우가 많다. 심지어 시스템에 대한 모델을 정확 히 알지 못하는 경우에는 제어기 설계 자체를 하지 못하 는 경우도 있다.

본 논문은 로봇에서 사용되는 대표적인 구동기인 모터 를 크게 바퀴구동 모터와 관절구동 모터로 나누고, 바퀴구 동 모터의 속도 추종과 관절구동 모터의 위치 추종을 위 한 최소 제어 인자 선정하는 방법을 제안하고 이를 통해 제어 이론에 익숙하지 사용자를 위한 사용자 편의성이 높 으며 임베디드 시스템에 적합한 가벼운 제어 시스템 설계 를 목표로 한다. 새로운 제어 이론의 제안보다는 기존의 널리 사용되는 검증된 제어기를 활용하여 사용편의성을 높이는 것에 중점을 두었다.

이를 위해 두 가지 경우에 대한 공칭 모델(nominal model)을 구하고 간단한 사용자 입력 제어 인자를 선정하 여 간편하며 외란과 모델링 인자 오차의 변동 등을 효율 적으로 제거할 수 있는 강인 제어 알고리즘을 개발하고 모의 실험과 실험을 통해 성능을 검증 하였다.

강인 제어 이론 중에는 대표적으로 MPC(Model Predictive Control)^[5], H-∞(H-infinity)^[6], DOB(Disturbance Observer based Control)^[7] 등이 있는데 이 중 외란 관측기(Disturbance Observer, DOB)는 PID 제어기처럼 설계가 비교적 쉽고 성 능이 좋아서 1990년대 후반부터 많이 활용되어 왔다^[8]. 외 란 관측기 기반의 제어 시스템은 외란, 모델링 오차, 매개 변수의 변화를 모두 외란으로 다루어 제거하여 실제 모델 (real model)를 공칭 모델처럼 거동하도록 만들어 주는 역할 을 한다^[9-12]. 본 논문에서는 바퀴구동 모터와 관절구동 모 터 시스템에 대한 외란 관측기 기반의 제어 시스템과 PID 제어 시스템의 성능을 모의 실험과 실제 모션제어 실험을 통해 비교 하였으며 이를 통해 외란 관측기 기반의 강인 제어 시스템의 성능을 검증하였다.

Katoh와 Fujiwara^[13]는 본 논문에서 제시한 방법과 유사 한 2 자유도 강인 제어기를 설계하고 자동 이득 조절(auto gain tuning) 방법을 제안하였으나, 제어기 설계가 복잡하고 고려해야 할 인자가 많기 때문에 초보자가 쉽게 사용하기 에는 무리가 있다. 이동 로봇의 바퀴구동 모터에 적용이 가능한 자동 이득 조절 방법도 제안된 바 있으나^[14], 이 역시 제어 성능을 극대화하기 위해서 복잡한 제어기를 설 계해야 하는 단점이 있다.

2장에서는 외란 관측기 기반의 제어 시스템 설계에 대 해 소개하고 바퀴구동 모터와 관절구동 모터 각각에 대한 동역학 시스템 모델링을 수행 하였다. 3장에서는 최소 제 어 인자를 도출하는 과정을 설명하고, 4장에서는 이를 기 반으로 두 가지 시스템에 대한 모의 실험을 실시 하여 PID 제어기와 DOB 제어의 성능을 비교하였고, 5장에서는 실제 제어 실험을 통해 두 가지 시스템이 모의 실험과 동 일한 결과를 보이는지에 대한 검증을 수행하였다.

2. 제어시스템 설계

2.1. 외란 관측기의 구조

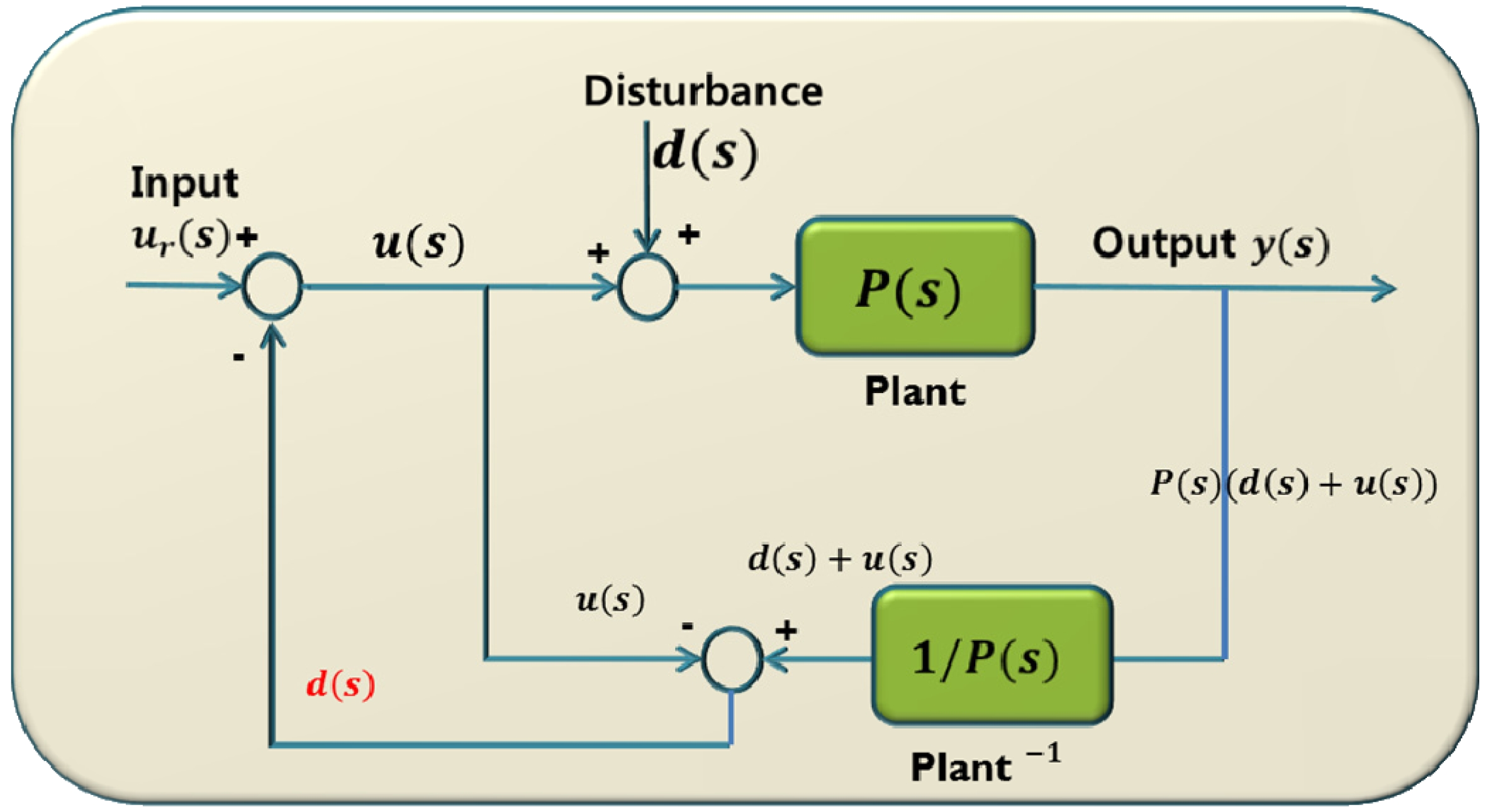
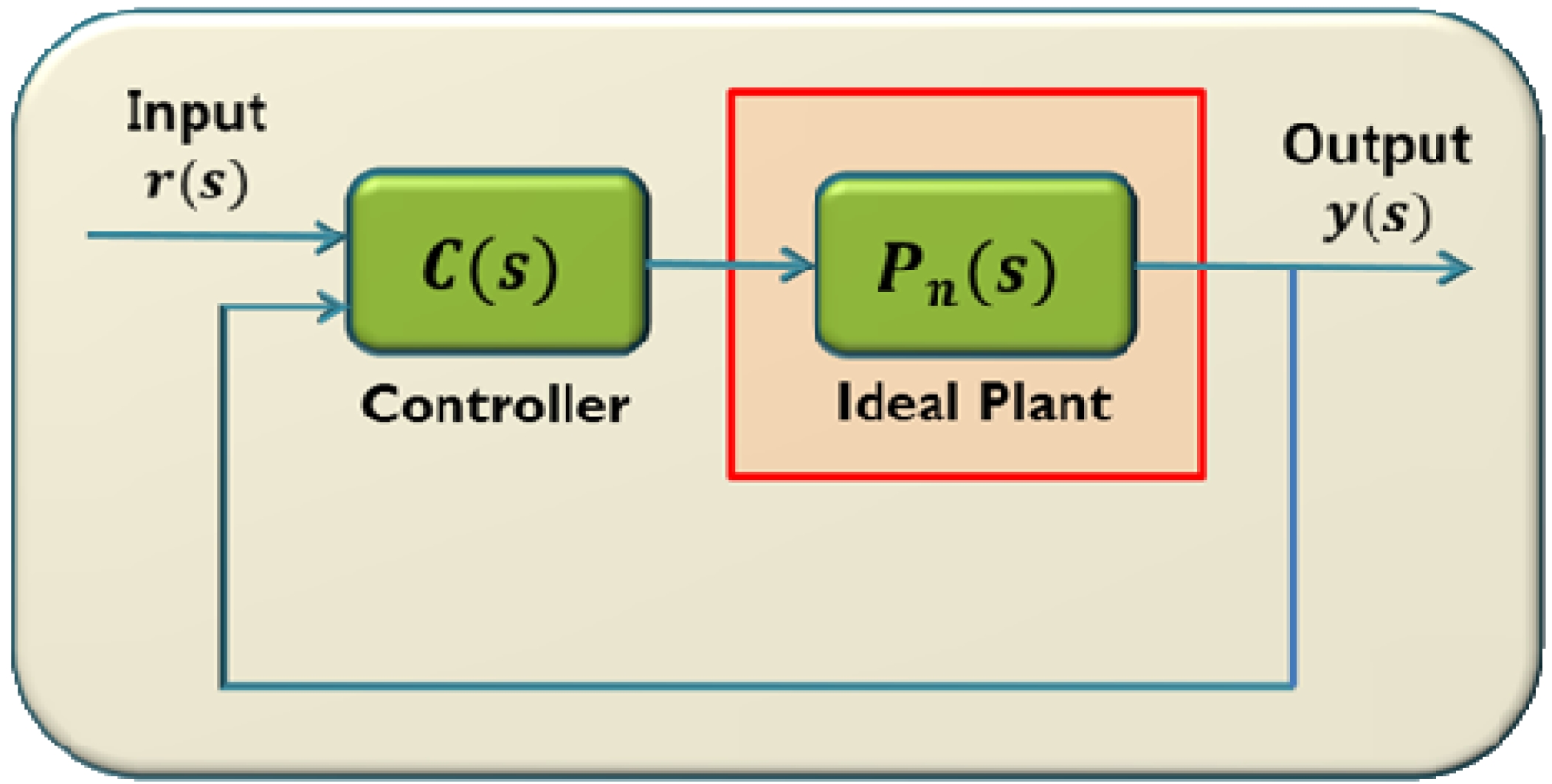
그림 1은 일반적인 외란 관측기의 블록선도이다. 이 때 의 출력 값, y(s)은 식(1)과 같다.

Fig. 1

Block diagram of DOB based control system

$$ y\left(s\right)=P\left(s\right)\left[u\left(s\right)+d\left(s\right)\right]$$

(1)

여기서 P(s)는 시스템의 전달함수, u(s)는 외란을 제거하기 위 한 인자를 포함한 제어 입력이며, d(s)는 외란을 의미한다.

이 때 외란 d(s)은 식(3)과 같으며,

$$ u\left(s\right)+d\left(s\right)=\frac{1}{P\left(s\right)}y\left(s\right)$$

(2)

$$ d\left(s\right)=\frac{1}{P\left(s\right)}y\left(s\right)-u\left(s\right)$$

(3)

피드백 입력 값 u(s)는 식(5)와 같다.

$$ u\left(s\right)=u_r\left(s\right)-\left(\frac{1}{P\left(s\right)}y\left(s\right)-u\left(s\right)\right)$$

(4)

$$ u\left(s\right)=u_r-d\left(s\right)$$

(5)

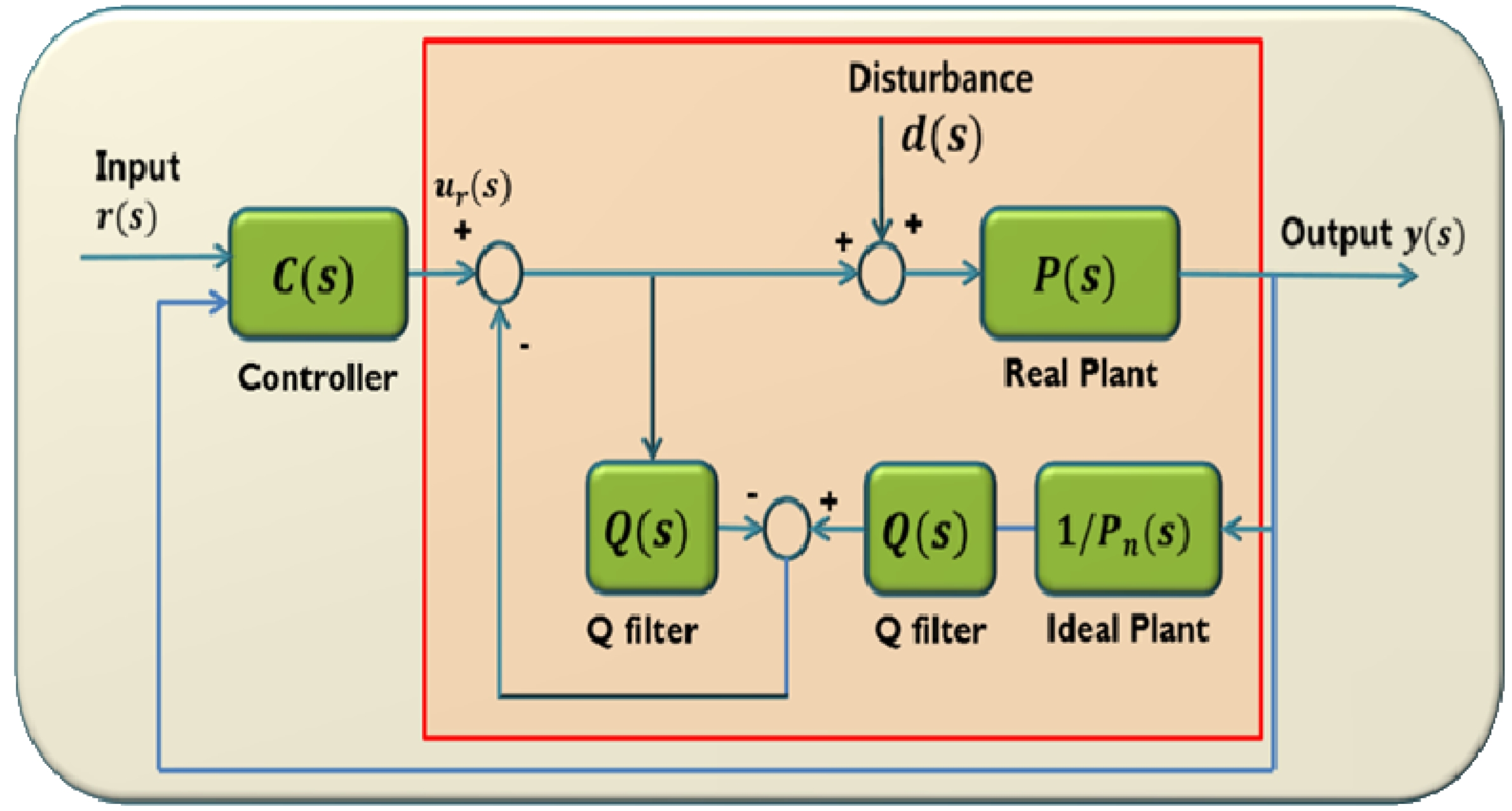
이론적으로는 사용자 제어 입력(u_r(s))에서 외란이 완전 히 제거된 입력 값 u(s)가 모델 P(s)에 인가된다. 그러나 식 (2)~(5)의 실제 모델의 역 모델을 구현하는 것은 현실적으 로 불가능 하므로 저주파 필터인 Q-filter를 사용하게 된다. 그림 2에서 보는 바와 같이 DOB 기반의 제어 시스템은 내부루프와 외부루프로 구성된다. 내부 루프는 외란, 모델 링오차, 시스템의 변화로 인해 발생하는 공칭 모델과의 오 차를 보상하도록 제어 입력을 생성하는 부분이며 외부루 프는 공칭 모델의 명령을 추종하도록 하여 제어 입력을 생성하는 부분이다.

Fig. 2

Structure of the DOB system (real plant)

즉, 외란 관측기는 그림 2의 사각형 영역에서처럼 제어 시스템의 실제 제어 대상인 P(s)와 Q-filter, 외란을 포함한 이상적인 제어 대상인 P_n(s)를 구성한다. 이 때의 P_n(s)는 실제 모델 P(s)와 다른 공칭 모델이기 때문에 추가적으로 실제 외란 및 신호 잡음뿐 아니라 제어대상인 P(s)와 공칭 모델 사이의 모델링 오차까지도 외란으로 인식하게 된다. 외란 관측기를 통해 P(s)는 피드백 루프에 의해서 P_n(s)로 보정이 되며, 이론적으로 외란이 없는 이상적인 제어 대상 인 공칭 모델 P_n(s)와 같이 사용자가 원하는 형태로 거동하 게 만들 수 있다. 결과적으로 외란 관측기는 외란, 모델링 오차, 매개변수의 변화를 모두 외란으로 다루어 제거하여 실제 모델을 공칭 모델처럼 거동하도록 만들어 주는 역할 을 한다.

그렇다고 터무니 없는 공칭 모델을 설계한다고 해서 원 하는 대로 동작하는 것은 아니며, 실제 모델의 시스템 차 수 및 형태가 비슷한 모델을 선정해야 좋은 결과를 얻을 수 있다. 그러나 이 역시 시스템 모델링에 대한 이해나 제 어에 익숙지 않은 사람들에게는 쉬운 일이 아니다. 이를 해결하기 위해 모델에 대한 시스템 식별(Identification)과 선 형화를 통하여 공칭 모델을 선정하고, 이를 제어하는 모델 기반(Model-based) 방법과 모델이 아닌 실제 모델의 입출력 데이터를 토대로 제어기의 이득 값들을 반복 조절하는 모 델이 필요 없는(Model-free) 방법 등이 있다.

하지만 본 논문의 목적은 누구나 쉽게 사용할 수 있고 임베디드 시스템에 쉽게 적용이 가능한 가벼운 제어기 개 발에 있다. 따라서 상기 방법보다는 로봇에 널리 사용되는 두 가지 시스템 모델인 바퀴구동 모터 시스템과 관절구동 모터 시스템에 대한 시스템 모델링을 통해서 시스템 차수 와 가장 적합한 공칭 모델을 도출하여 쉽게 제어를 수행 할 수 있는 방법을 제안하고자 한다.

2.2. 동역학 방정식 및 시스템 모델링

2.2.1. 바퀴구동 모터

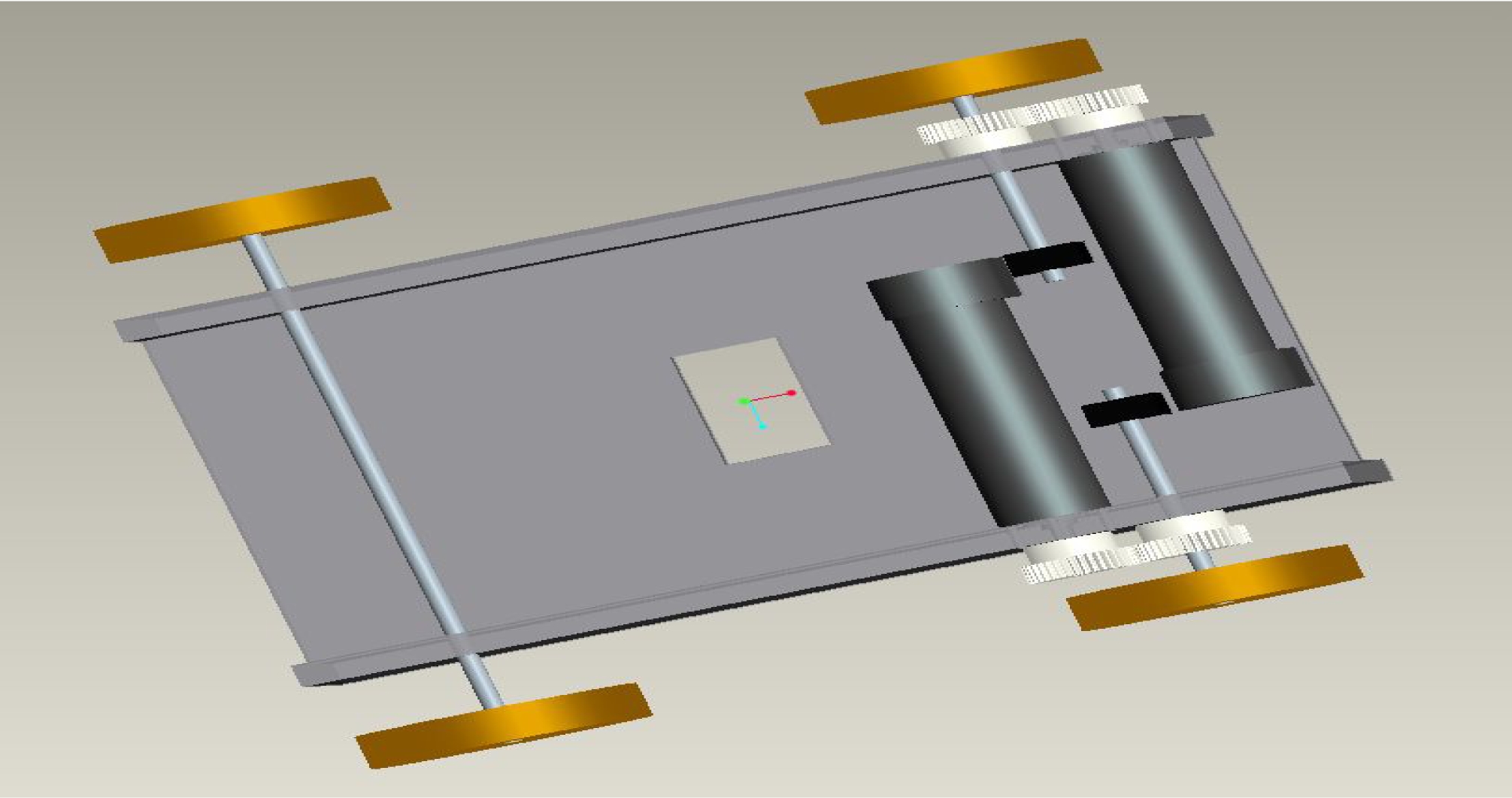
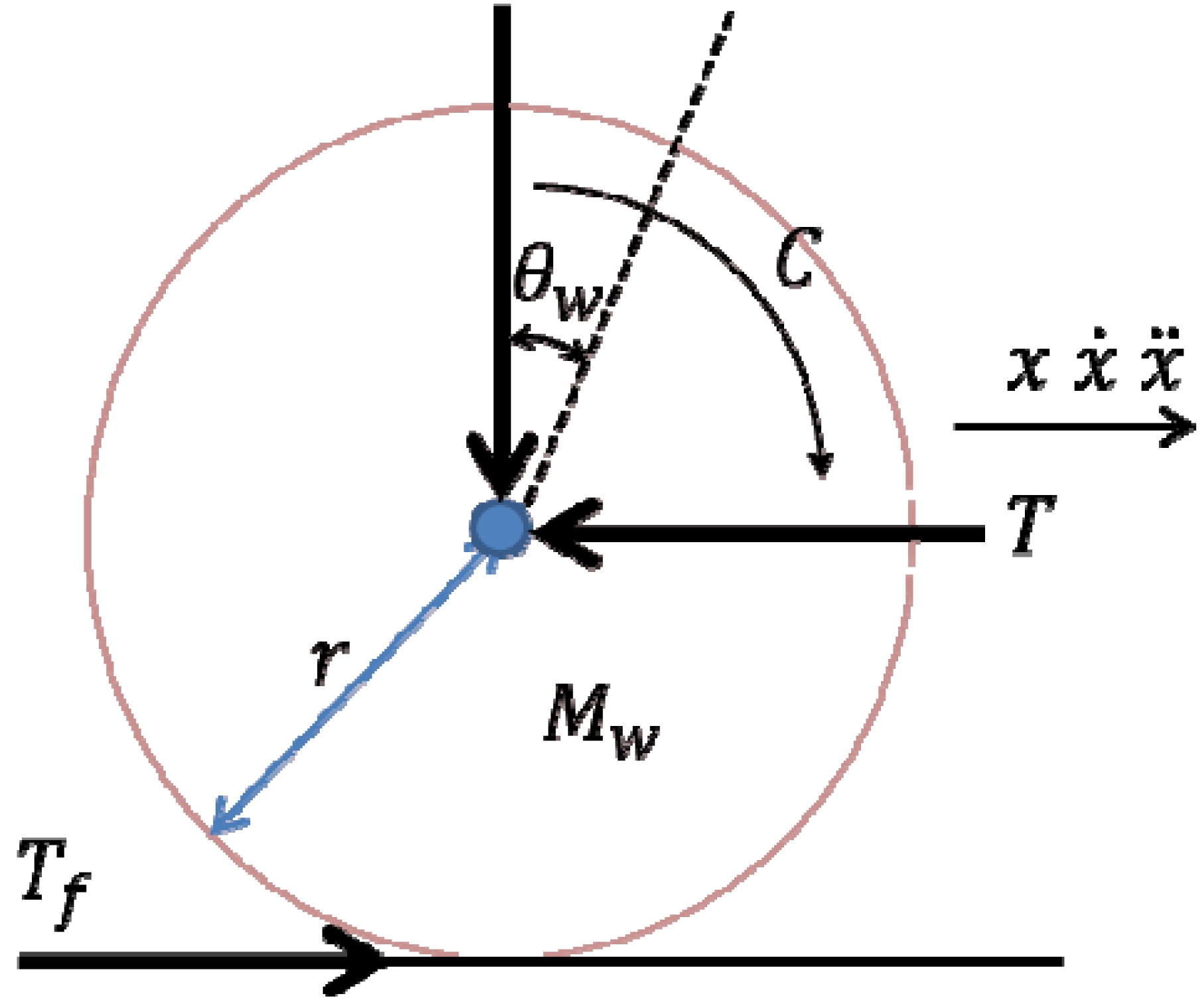
본 논문에서는 두 가지 시스템에 대한 모델링을 수행하 였으며, 첫째로 그림 4와 같은 바퀴구동 모터에 대한 기구 부의 동역학 모델링을 라그랑지(Lagrange) 방법을 이용하 여 유도하였다. 우선 기어 내장 모터의 동역학 방정식은 기어의 관성 모멘트가 무시할 정도로 작다고 가정하면 아 래의 식과 같다.

Fig. 4

Mechanism of wheel drive motor system

Fig. 5

Free body diagram of wheel

$$ T={\mathit{nk}}_{t}i-f_m\stackrel{.}{\mathit{\theta }}-J_m\stackrel{..}{\mathit{\theta }}$$

(6)

$$ L\stackrel{\cdot }{i}+R_{m}i=V-k_b\stackrel{.}{\mathit{\theta }}$$

(7)

여기서 모터의 토크 T는 전류 i와 토크상수 k_t의 곱이며 n은 기어 비를 나타낸다. f_m은 회전 마찰 계수, J_m은 모터의 회전 관성이며, θ는 모터의 회전 각이다. 식(7)에서 L은 모 터 코일의 인덕턴스, R_m은 저항, k_b는 역기전력 상수, i는 전 류, V는 전압을 의미한다. 여기서 모터의 인덕턴스를 0으로 가정하면 모터의 구동 토크는 식(9)와 같다.

$$ i=\frac{1}{R_m}\left(V-k_b\stackrel{.}{\mathit{\theta }}\right)$$

(8)

$$ T=\frac{{\mathit{nk}}_t}{R_m}\left(V-k_b\stackrel{.}{\mathit{\theta }}\right)-f_m\stackrel{.}{\mathit{\theta }}-J_m\stackrel{..}{\mathit{\theta }}$$

(9)

또한 이동 로봇과 바퀴의 경우 직선 운동 만을 한다고 가정하고, 자유 물체도를 통해 운동방정식을 구하면 식 (10)-(12)와 같다.

$$ T_{\mathit{wT}}=\frac{1}{2}{M}_w{\stackrel{.}{x}}^2$$

(10)

$$ T_{\mathit{wR}}=\frac{1}{2}{J}_w{\stackrel{.}{\mathit{\theta }}}^2$$

(11)

$$ T_c=\frac{1}{2}{m}_c{\stackrel{.}{x}}^2$$

(12)

여기서 M_w는 바퀴 무게, J_w는 바퀴 관성, m_c는 이동 로봇의 무게를 나타내며, x는 이동 로봇의 이동 거리, r은 바퀴의 반지름을 의미한다. 따라서 T_wT는 바퀴의 병진 운동에너지 이고 T_wR은 회전 운동에너지이다. 그리고 T_c는 이동 로봇의 운동에너지를 나타낸다. 이를 통해 바퀴 하나에 대한 라그 랑지안(Lagrangian)과 라그랑지 방정식을 이용하면 바퀴구 동 모터에 의해 구동되는 기구에 포함된 바퀴 구동 모터 의 동역학 방정식은 식(13)과 같다.

$$ \left(M_w{r}^2+\frac{1}{4}{m}_c{r}^2+J_w+J_m\right)\stackrel{..}{\mathit{\theta }}+\left(\frac{{\mathit{nk}}_t{k}_b}{R_m}+f_m\right)\stackrel{.}{\mathit{\theta }}=\frac{{\mathit{nk}}_t}{R_m}V-T_f$$

(13)

여기서 T_f는 바퀴의 마찰력을 의미하며, 바닥의 상태 및 시스템 하중에 의해서 계속해서 변하기 때문에 정확한 모 델링이 쉽지 않다. 따라서 외란으로 가정하고 무시한다. 식(13)을 최종적으로 인가전압에 대한 각속도의 전달함수 로 나타내면 식(14)와 같다.

$$ \frac{\mathit{\omega }}{V}=\frac{{\mathit{nk}}_t/R_m}{\left(M_w{r}^2+m_c{r}^2/4+J_w+J_m\right)s+\left({\mathit{nk}}_t{k}_b/R_m+f_m\right)}$$

(14)

2.2.2. 관절 구동 모터

다음으로 그림 6과 같은 로봇 관절구동 모터에 대한 시 스템 모델링을 수행하였다. 제어 환경은 크게 구동기(DC 모터)와 제어할 기계시스템(빔)으로 나눌 수 있으며 앞서 수행한 바퀴구동 모터 시스템과 동일한 과정으로 모델링 이 가능하다. 구동기의 경우 바퀴구동 모터와 동일하게 식 (6), (7)과 같으며, 기계시스템은 바퀴구동 시스템에 비해 단순하며, 빔의 회전 모멘트(J₀)만 고려해주면 아래와 같은 식이 된다.

Fig. 6

Mechanism of joint drive motor system

$$ T=J_0\stackrel{..}{\mathit{\theta }}$$

(15)

바퀴구동 시스템과 동일하게 모터의 인덕턴스를 0으로 가정하면 식(16)과 같은 식이 유도된다.

$$ T=J_0\stackrel{..}{\mathit{\theta }}=\frac{{\mathit{nk}}_t}{R_m}\left(V-k_b\stackrel{.}{\mathit{\theta }}\right)-f_m\stackrel{.}{\mathit{\theta }}-J_m\stackrel{..}{\mathit{\theta }}$$

(16)

최종적으로 인가전압에 대한 각도의 전달함수로 나타내 면 식(17)과 같은 식으로 유도가 가능하다.

$$ \frac{\mathrm{\Theta }}{V}=\frac{{\mathit{nk}}_t/R_m}{\left(J_0+J_m\right)s^2+\left({\mathit{nk}}_t{k}_b/R_m+f_m\right)s}$$

(17)

3. 최소 제어 인자 도출

제어에 대한 이론이 부족한 사용자를 위한 최소 제어 인자를 도출하기 위해서 필요한 제어 요소를 도출해 보기 로 하자. DOB를 이용한 제어기 설계에서 사용자가 고려해 야 하는 제어 인자는 다음과 같다.

1. 공칭 모델
2. Q-filter 설계
3. 제어기 형태 및 변수 설계 (그림3의 C(s))

Fig. 3

Structure of the DOB system (nominal plant)

첫째, 공칭 모델은 2.1절에서 설명한 바와 같이 제어 대 상 시스템과 근사한 형태로 이루어져야 한다. 따라서 모든 제어 시스템에 적합한 공칭 모델이라는 것은 정의하기 어 렵다. 하지만 본 논문에서는 로봇 제작에서 가장 빈번히 사용되는 모델인 바퀴구동 모터 및 관절구동 모터로 한정 하였기 때문에 2가지 형태에 대해서만 고려하기로 하며, 거의 대부분의 경우를 포함할 수 있다. 둘째, Q-filter의 형 태는 2.3절에서 설명한 안정적인 성능을 보이면서도 설계 가 간편한 이항식 형태의 Q-filter를 사용하고자 한다. 마지 막으로 제어기 설계에서는 외란 관측기의 내부 루프가 잘 동작한다고 가정하면 기본적인 PID 제어기와 이상적인 시 스템에 대한 제어 인자로 제어기를 설계할 수 있다.

4. 모의 실험

4장과 5장에서는 모의 실험과 실험을 통해 제어 성능을 살펴봄으로써 제안한 방법의 유효성을 검증하고자 한다.

모의 실험과 실험에서 비교 대상으로 사용한 PI/PD 제 어기의 경우 MATLAB의 자동 이득 조절 도구를 이용하여 최대의 성능을 내도록 이득 값을 설정하였다. 바퀴구동 모 터의 속도 추종 제어의 경우 속도에 대한 PI 제어기를 사 용하였는데, 이는 위치 제어에서의 PD 제어기와 동일하며, 속도 추종 제어에서 PID 제어기는 속도의 미분 값이 필요 하기 때문에 성능이 오히려 나빠지는 경향이 있어서 일반 적으로 사용하지 않는다. 관절구동 모터의 위치 제어에는 PD 제어기를 사용하였는데, PID 제어기에 비해서 안정성 이 높으며, 빠른 응답 특성을 보여주기 때문이다.

4.1. DOB 설계 및 Q-filter 선정

모의 실험은 MATLAB Simulink를 이용하여 실시하였다. 식(20), (21)은 각각 바퀴구동과 관절 구동 모터 시스템에 사용된 Q-filter를 나타내며 본 연구에서의 τ값은 0.01이다. 실험에서 사용한 모터의 기계적 시정수 값이 0.001이므로 10배 값을 사용하였다. Q-filter의 형태 선정에 따른 실험결 과는 큰 차이를 보이지 않았기 때문에, 가장 안정적이면서 널리 쓰이는 형태를 선정하였다.

$$ Q_{10}=\frac{1}{1+\mathit{\tau }\cdot s}$$

(20)

$$ Q_{31}=\frac{3\mathit{\tau }+1}{1+3\mathit{\tau }\cdot s+{3\mathit{\tau }}^2\cdot s^2+{\mathit{\tau }}^3\cdot s^3}$$

(21)

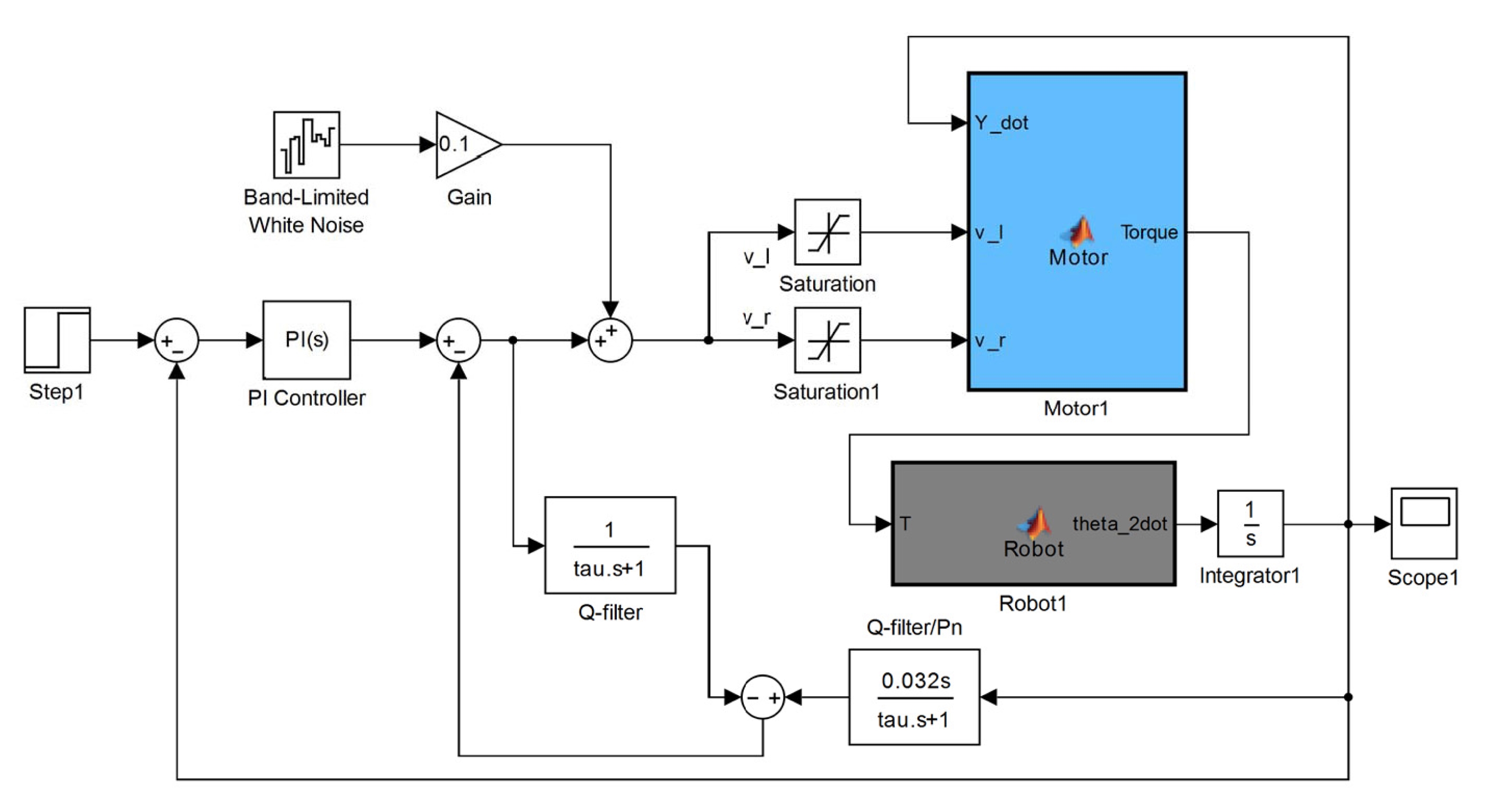
DOB 기반의 속도추종 강인 제어기 설계를 위해 DOB 내부루프와 PI/PD 제어기를 함께 사용하였으며 그림 7은 바퀴구동 모터 시스템의 전체 Simulink 블록도를 나타낸다.

Fig. 7

Configuration of the DOB based robust control system-Wheel drive motor system

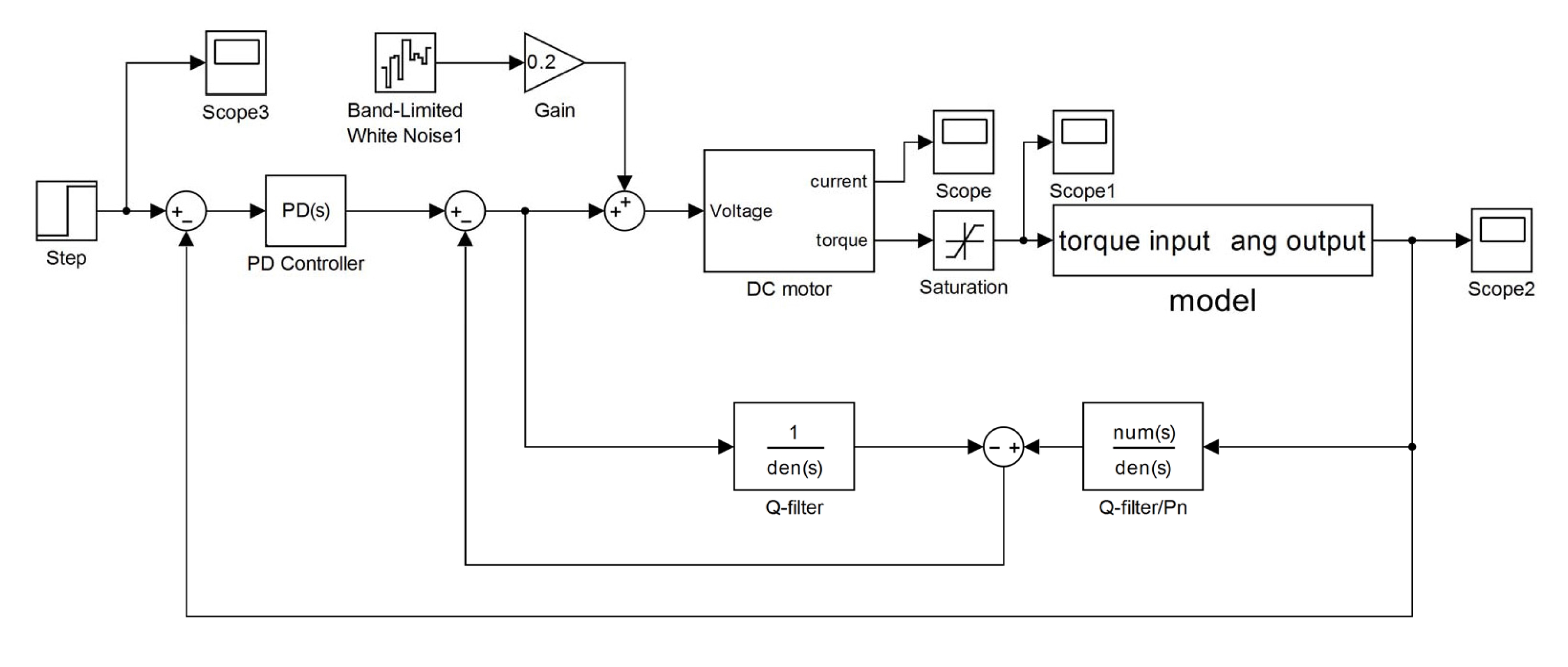
관절구동 모터 시스템은 Simscape 모델링을 이용하였으 며 그림 8은 이에 관한 전체 Simulink 블록도를 나타낸다.

Fig. 8

Configuration of the DOB based robust control system-Arms drive motor system

4.2. 모의 실험 결과

4.2.1. 바퀴구동 모터

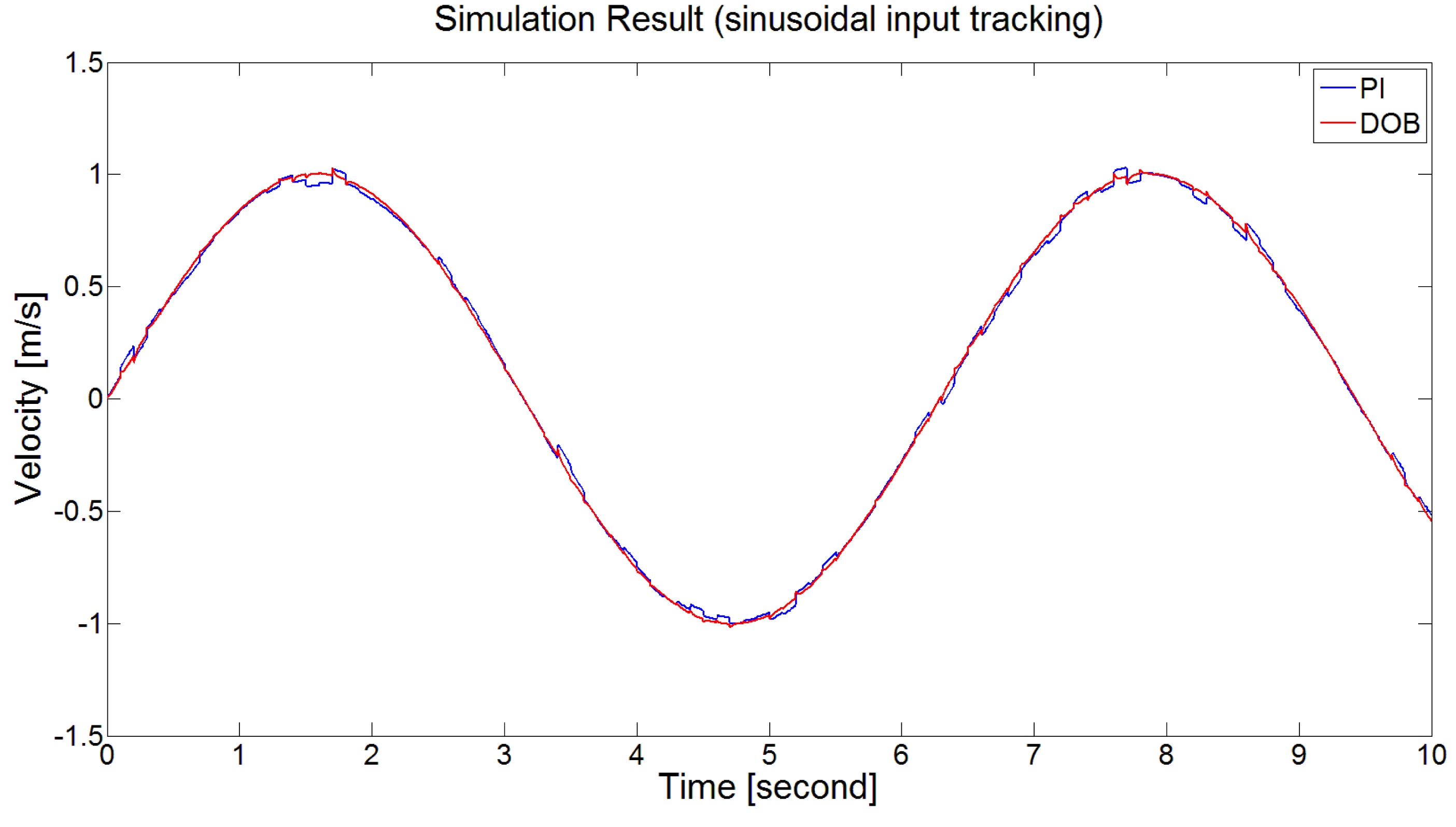
DOB기반 제어기의 외란 제거 성능을 관찰하기 위해 PI 제어기만을 사용한 경우와 PI 제어기를 DOB와 함께 사용 한 경우 각각에 정현파 입력과 외란을 인가했을 때의 응 답특성을 확인하였다.

그림 9에서 보는 바와 같이 DOB 기반의 제어기가 PI 제어기만을 사용했을 때 보다 외란 제거 성능이 뛰어난 것을 모의 실험을 통해 확인할 수 있다.

Fig. 9

Velocity tracking simulation result

4.2.2. 관절구동 모터

관절구동 모터는 Q₃₁ 필터를 이용한 DOB 기반의 제어 기와 PD 제어기를 설계하여 각각의 위치추종 성능을 비교 하였다.

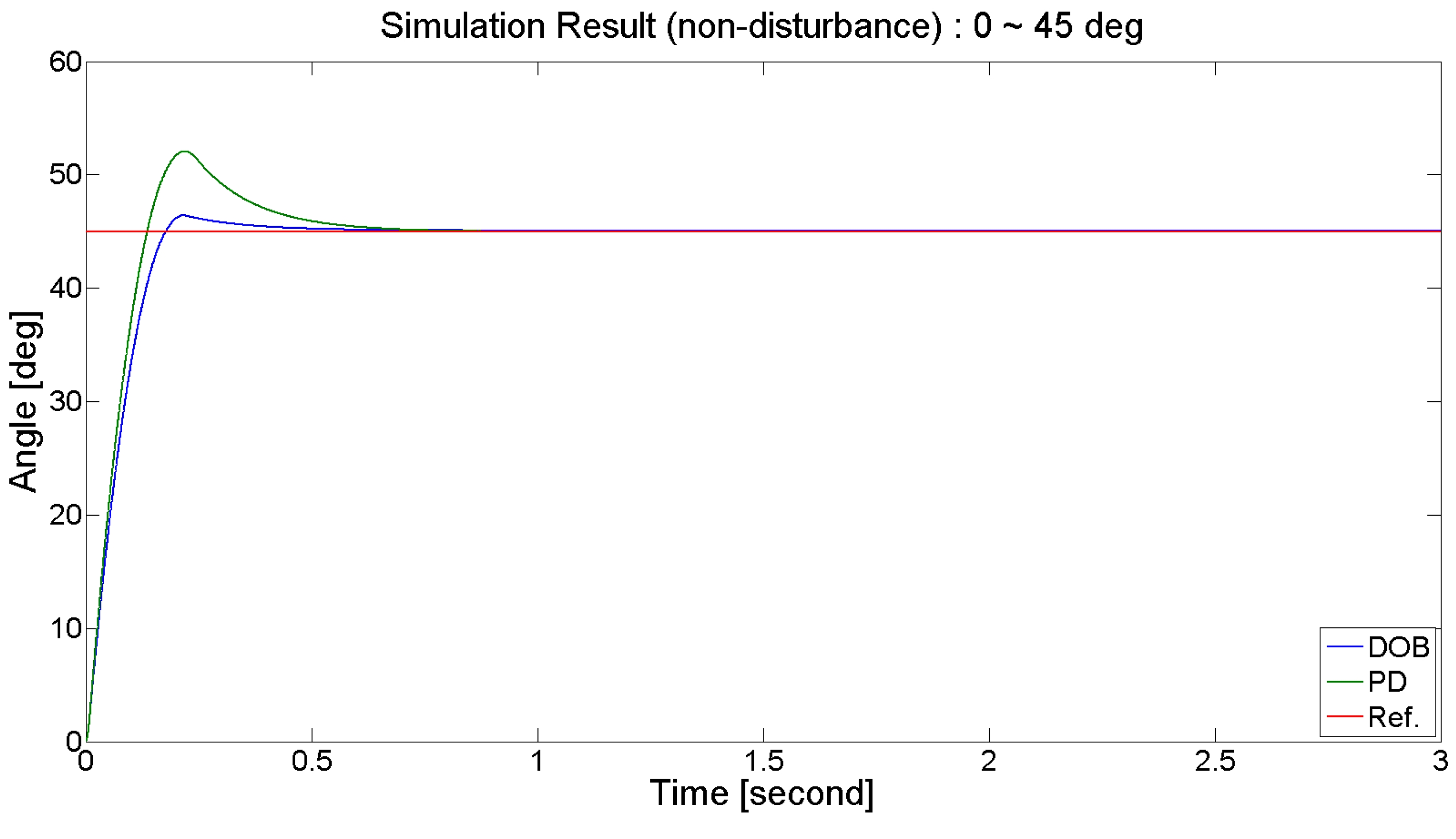
그림 10은 외란이 없을 때 0°~45°로의 위치제어 결과를 나타낸다. DOB 기반의 제어가 PD 제어만을 사용했을 때 보다 오버슈트(overshoot)가 적음을 확일 할 수 있으며 정 상상태에 안정적으로 수렴하는 것을 확인 할 수 있다.

Fig. 10

Position control with non-disturbance input

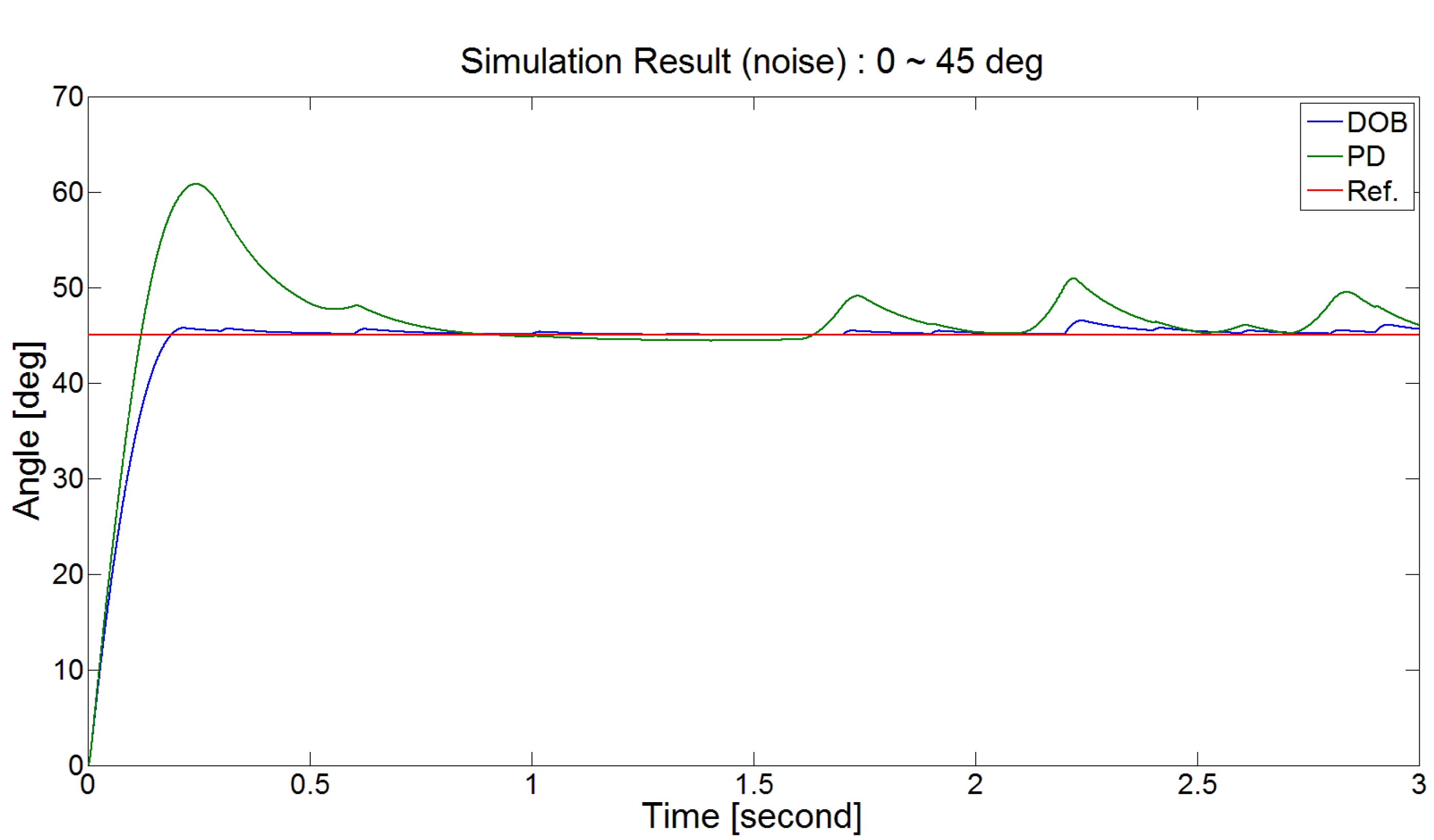
그림 11은 외란을 인가했을 때의 모의 실험 결과를 나 타내며 DOB 기반의 제어가 외란 제거 성능이 뛰어남을 보여 준다.

Fig. 11

Position control with disturbance input

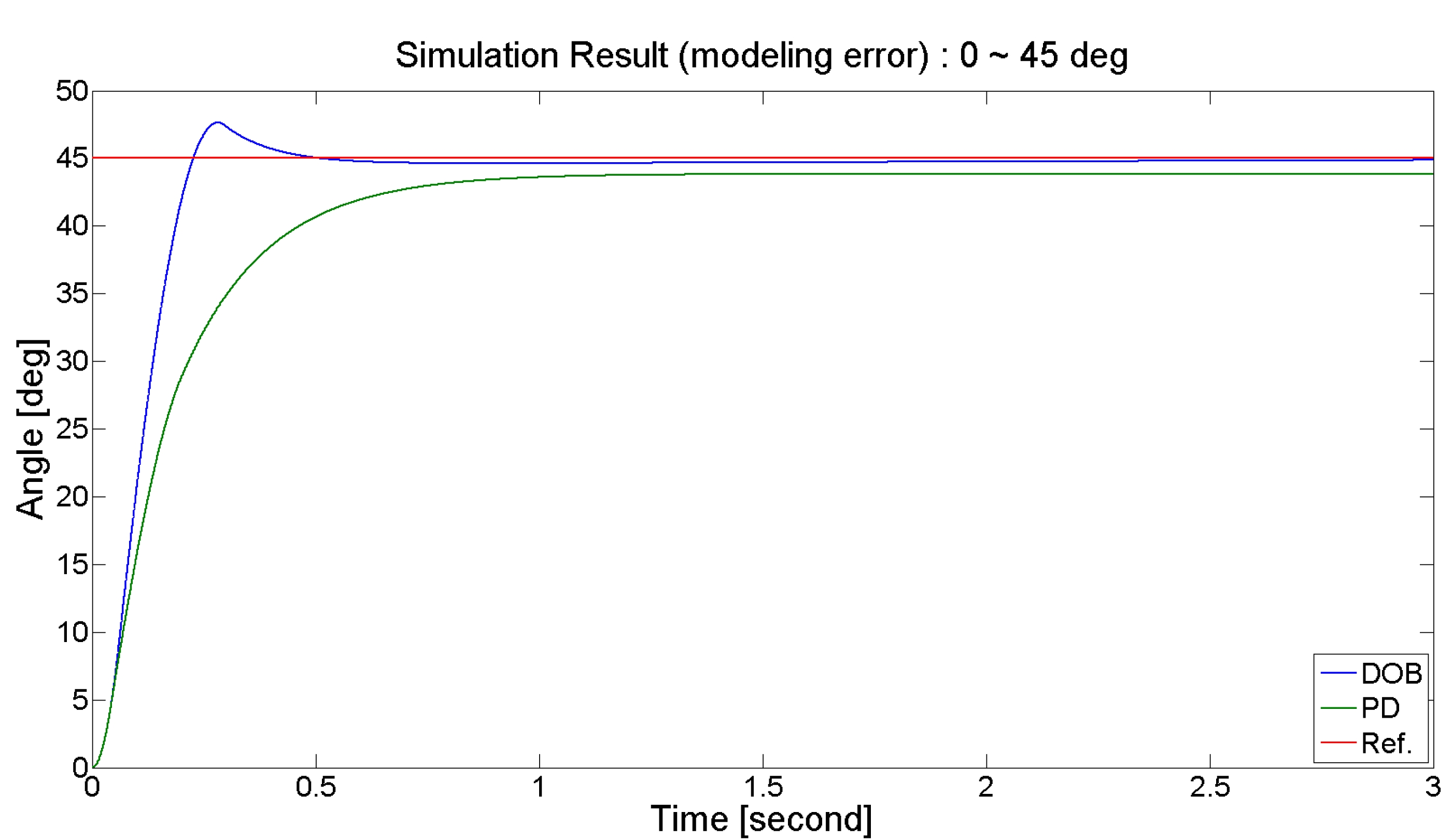
그림 12는 모델링 오차에 대한 제어성능을 비교하기 위 해서, 빔의 무게를 10배로 증가시켰을 때의 결과를 나타낸 다. PD 제어기의 경우 응답시간이 3배정도 더 걸리는 것을 확인할 수 있는 반면, DOB 기반의 제어기의 경우 외란이 없을 때와 차이가 거의 없는 것을 확인할 수 있다. 이를 통해 DOB 기반의 제어기가 무게 변화(인자 변화)에도 강 인한 제어 성능을 보이는 것을 확인 할 수 있다.

Fig. 12

Position control with vague modeling parameter

5. 실험 및 결과

5.1. 하드웨어 및 기구부 구성

5.1.1. 바퀴구동 모터

바퀴구동을 위한 DC 모터로는 Maxon사의 기어, 엔코더 (encoder) 내장형 249529, 118752 모델을 사용하였으며 모터 컨트롤러는 동일 회사의 145391 모델을 사용하였다. 제어 실험을 위해 NI DAQ PCI-6221 모델을 사용하였으며 그림 13(a)는 기구부 구성을 나타내며 그림 13(b)는 실험장치의 모습을 나타낸다.

Fig. 13

(a) Wheel drive motor mechanism (b) Experiment environment

그림 13(b)에서 보는 바와 같이 기구부를 PCI와 유선으 로 연결하여 LabVIEW를 이용하여 제작한 컨트롤 인터페 이스를 통해 제어 실험을 실시 하였다.

5.1.2. 관절구동 모터

관절구동 실험 또한 동일한 DC 모터를 사용하였으며 실험장치 구성은 그림 14와 같다.

Fig. 14

Arms drive motor mechanism

동일한 DAQ 모델을 사용하여 PC와 유선 연결 후 제어 실험을 실시 하였다.

모든 DOB 기반 제어기 설계 과정은 제안한 방식으로 사용자로부터 입력을 받아서 진행하였으며 추가적인 제어 이득 조절 등은 수행하지 않았다. 비교 대상으로 사용한 PI/PD 제어기의 경우에는 앞서 언급한 것처럼 다수의 실 험을 수행하여 가장 좋은 결과를 얻는 이득 값 조정을 수 행한 결과이다.

5.2. 실험 결과 – 바퀴구동 모터의 속도 제어

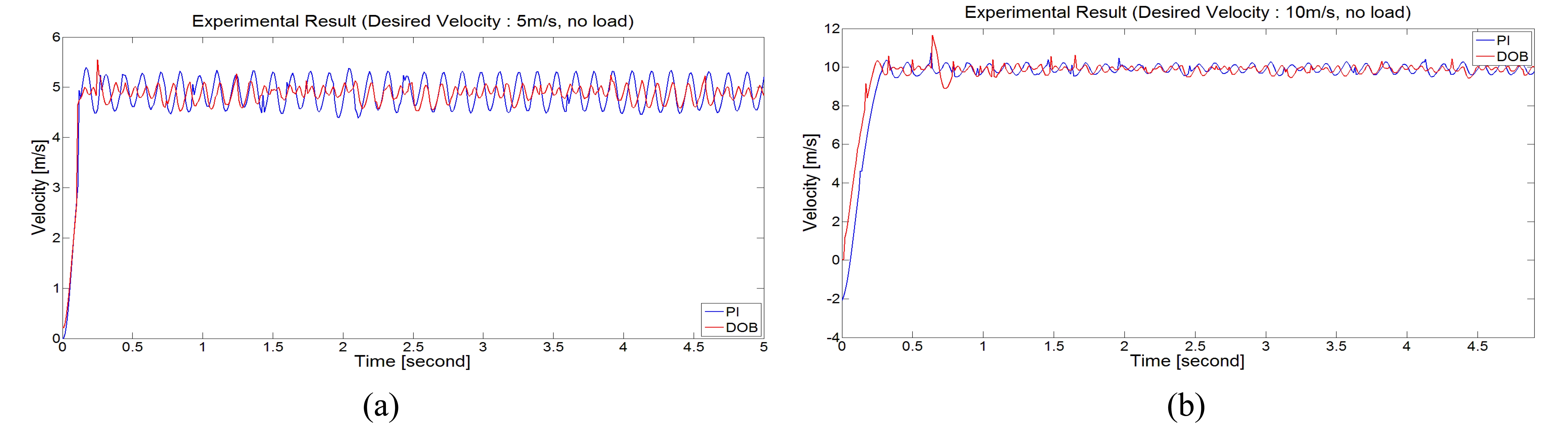
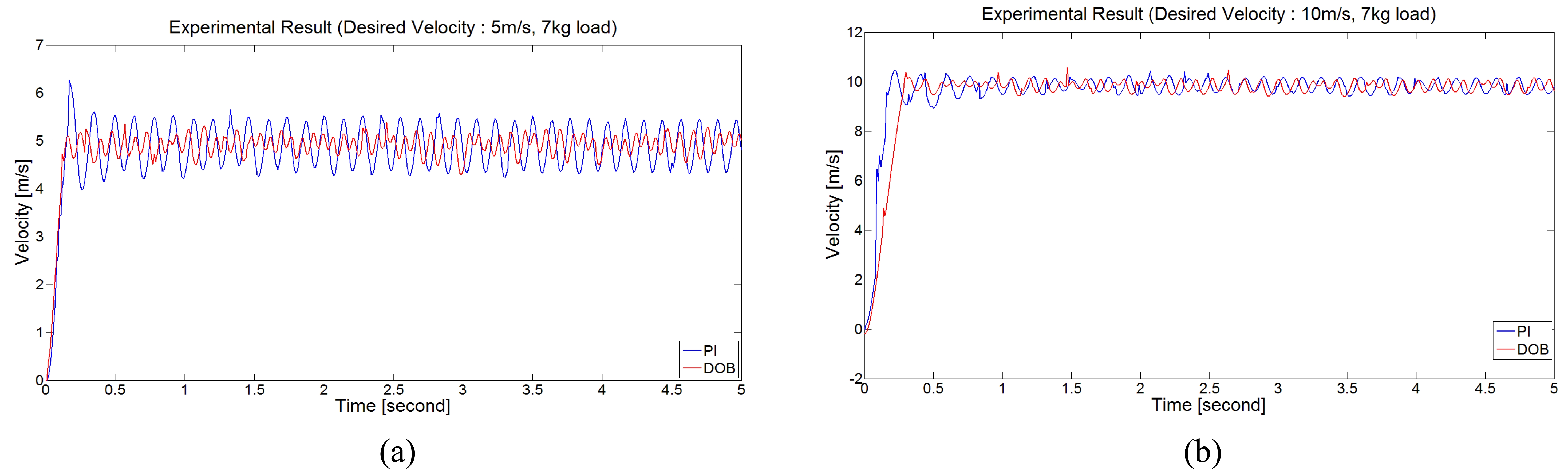
실험은 그림 13(b)에서와 같이 컨베이어벨트 위에서 주 행하도록 구성되었으며, 추가 하중이 없는 경우와 7000g의 하중을 기구부 위에 올려놓은 경우 두 가지 조건에서 실 시되었다. 또한 각각의 조건에 대해 5m/s와 10m/s의 속도 를 입력하였다. 실험에서는 PI 제어기만 사용했을 때와 DOB 기반의 제어기를 사용했을 때의 속도추종 성능을 비 교하였다. 그림 15는 하중이 없을 시 각각 5m/s와 10m/s의 속도를 입력했을 때의 결과를 나타낸다.

Fig. 15

Result of output velocity using PI and DOB with no load (a) 5m/s input, (b) 10m/s input

그림 16은 동일한 제어기에 대해 7000g 하중의 외란을 인가하였을 경우의 결과를 나타낸다. DOB 기반 제어기에 서는 큰 차이가 없지만, PI 기반 제어기의 경우 오차 폭이 더 커짐을 볼 수 있다.

Fig. 16

Result of output velocity using PI and DOB with 7000g load (a) 5m/s input, (b) 10m/s input

그림 15, 16에서와 같이 모든 실험결과에서 DOB 기반의 제 어가 PI제어기에 비해 오차범위가 작은 것을 알 수 있으며 외 란 제거 성능도 PI 제어기에 비해 우수함을 알 수 있다.

5.3. 실험 결과 – 관절구동 모터의 위치 제어

관절구동 모터의 위치제어는 그림 14의 관절 구동 모터 에 무게가 다른 빔을 연결하여 실시하였다. 하중의 무게가 280g, 530g 일 때와 하중이 없을 때 세 가지 경우에 대해 실험을 진행 하였으며 각각의 경우에 대해 PD 제어만을 사용했을 때와 DOB 기반 제어기를 사용했을 때의 제어 성능을 비교하였다.

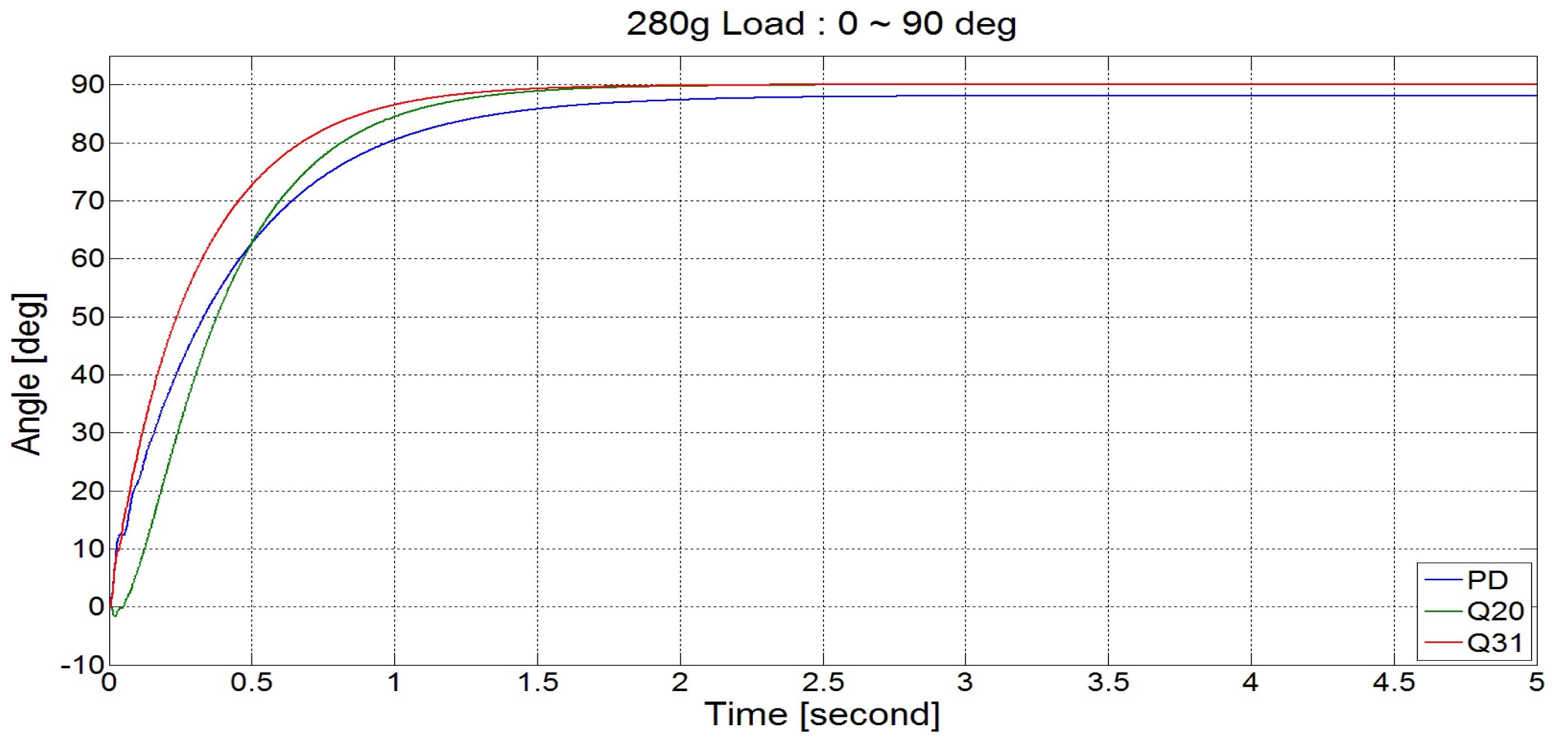
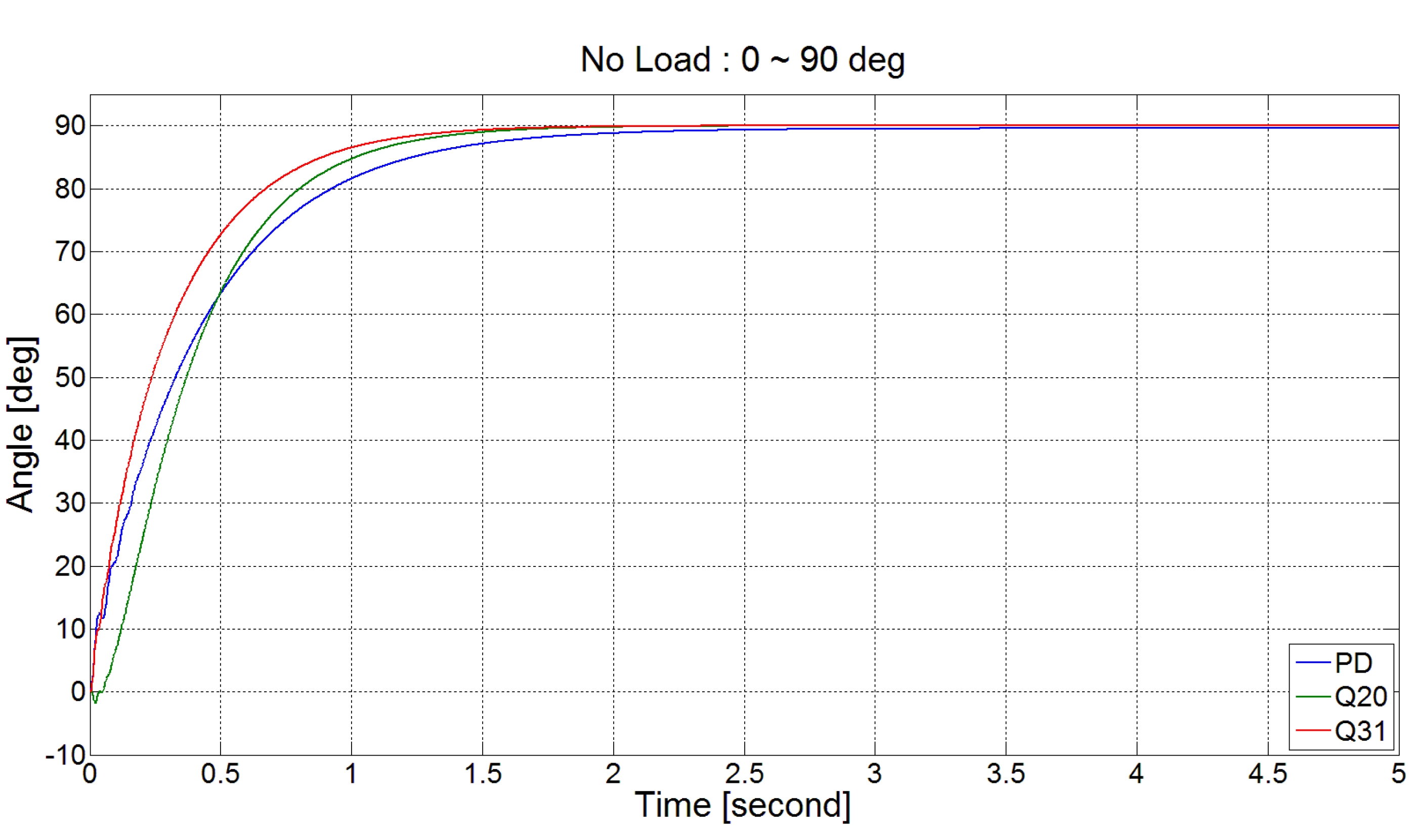
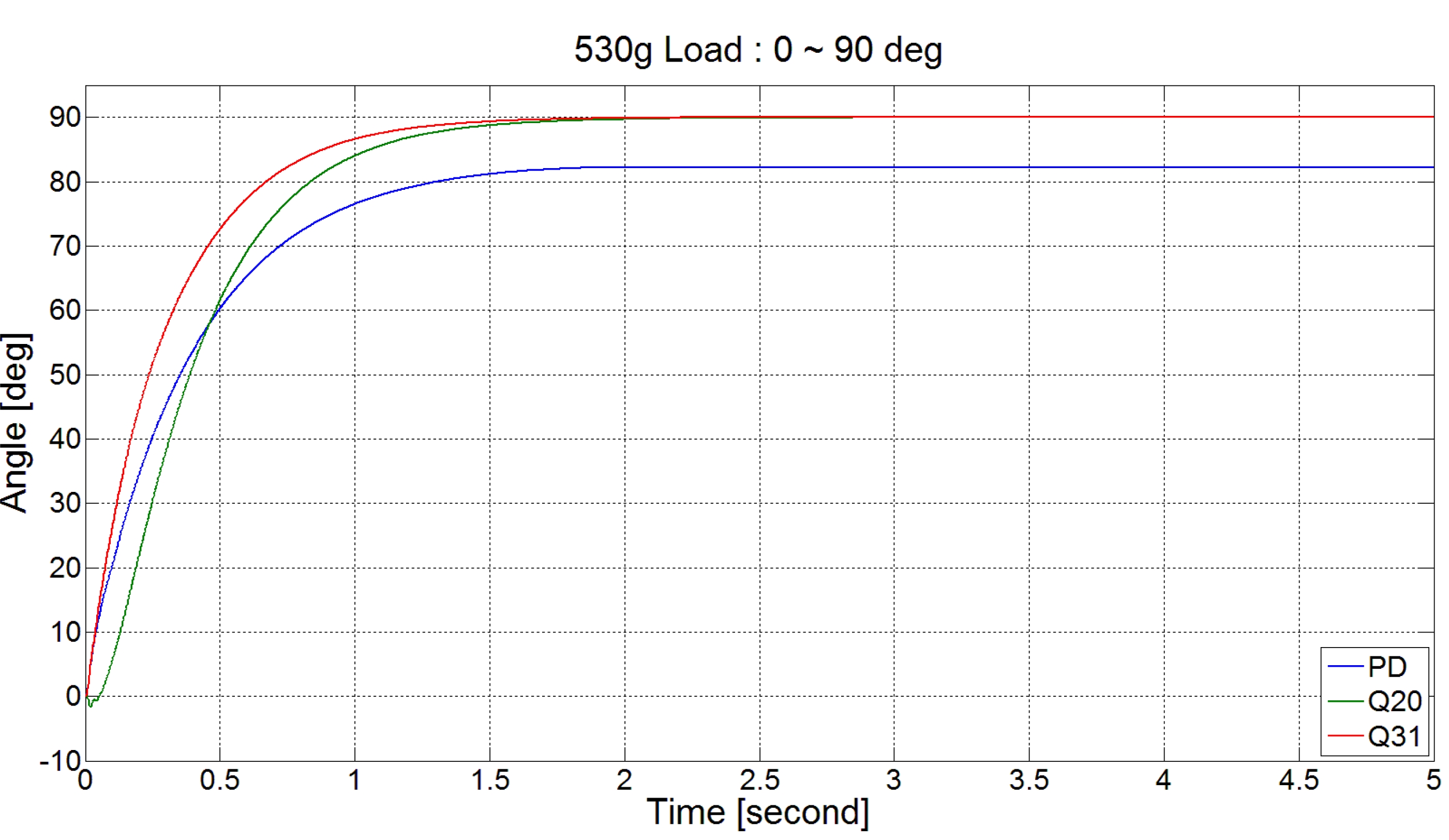
그림 17은 빔의 하중이 280g일 때 0°~90°로의 위치 제어 성능을 나타내며 각각의 경우에 PD제어, DOB(Q₂₀), DOB(Q₃₁)의 성능을 비교 하였다. 그림 18과 19는 하중이 없을 때와 하중이 530g 일때의 실험 결과를 나타낸다.

Fig. 17

Result using PD and DOB (280g load)

Fig. 18

Result using PD and DOB (no load)

그림 17-19의 결과를 보면 하중이 다른 세 가지 경우 모 두 Q31 필터를 사용한 DOB 기반의 제어 시스템이 빠른 응답속도로 정상상태에 안정적으로 도달하는 것을 확인 할 수 있다. 비교 대상으로 사용한 PD 제어기에 비해서 제 어 성능이 월등히 좋다고 할 수는 없지만, 제안한 제어기 의 경우에는 사용자의 입력으로 받은 값들만을 이용하여 제어 전문가가 정밀하게 조정한 PD 제어기의 제어 결과와 유사한 수준의 결과를 얻을 수 있었다. 따라서 사용자 편 의성이 높은 제어기 설계가 성능 면에서도 충분히 사용 가능하다는 것을 알 수 있다.

Fig. 19

Result using PD and DOB (530g load)

6. 결 론

본 논문에서는 강인제어에 대한 이론 및 DOB 기반의 제어 시스템 설계방법, 그리고 PID 제어기와의 모의 실험 과 실험을 통해 DOB 기반의 제어 시스템의 성능을 확인 하였다. 바퀴구동 모터의 실험을 통해 하중의 변화(주변 환경 및 인자 변화)에 대해 외란 극복 성능이 PI 제어기만 사용했을 때 보다 좋아짐을 확인 할 수 있었고, 관절 구동 모터 실험을 통해서도 인자 변화에 강인한 제어 성능을 보이는 것을 확인 할 수 있었다.

PID 제어만 사용했을 때에는 각각의 이득 값에 시스템 이 민감하게 반응하여 여러 번의 시행착오를 거쳐야 설계 가 가능하였다. 또한 하중의 변화, 주변환경의 변화, 모터 의 변화 등 여러 인자가 변했을 때에도 그에 맞는 이득 값 과 시스템 인자를 수정해야 한다. 반면 DOB 기반의 제어 기의 경우 이러한 변동에 대해 강인한 제어 성능을 보여 제어기에 익숙하지 않은 사용자 일지라도 쉽게 다룰 수 있음을 확인 할 수 있었다.

비록 제안한 방법으로 설계한 제어기의 성능이 시스템 의 최대 성능이라는 것을 보장할 수는 없지만, 사용자가 편리하게 설계가 가능하면서도 기본 성능을 보여준다는 장점을 보여주었다.

References

• Vaidya, J., “Motor selection for actuation systems”, (1995, Sep), Electrical Electronics Insulation Conference and Electrical Manufacturing & Coil Winding Conference, p385-391. [https://doi.org/10.1109/eeic.1995.482392]
• Fussell, B.K., Taft, C.K., “Brushless DC motor selection”, (1995, Sep), Electrical Electronics Insulation Conference and Electrical Manufacturing & Coil Winding Conference, p345-353. [https://doi.org/10.1109/eeic.1995.482388]
• Kimbrough, S., Dewell, L., “Electric Motor Selection for Motion Control Systems”, (1990, May), American Control Conference, p2079-2082. [https://doi.org/10.23919/acc.1990.4791096]
• Choi, C., Jung, S., Kim, S., Lee, J., Choe, T.S., Chung, S., Park, Y., “A motor selection technique for designing a manipulator”, (2007, Oct), International Conference on Control, Automation and Systems, p2487-2492. [https://doi.org/10.1109/iccas.2007.4406782]
• Morari, M., Lee, J.H., “Model predictive control: past, present and future”, Computers & Chemical Engineering, (1999), 23, p4-5. [https://doi.org/10.1016/s0098-1354(98)00301-9]
• Burl, J.B., Linear Optimal Control: H_2 and H_Infinity Methods, (1998), Addison-Wesley Longman Publishing Co., Inc.
• Choi, Y., Yang, K., Chung, W.K., Kim, H.R., Suh, I.H., “On the robustness and performance of disturbance observers for second-order systems”, IEEE Transactions on Automatic Control, (2003, Feb), 48(2), p315-320.
• Choi, H.T., “Analysis for understanding of disturbance observer and its general structure”, World of Electricity, (2011), 60(7), p31-40.
• Chang, Y.S., Keh, J.E., Lee, M.H., “Attitude Control of the Unmanned Robot System Using Disturbance Observer”, The Korean Institute of Electrical Engineers, (2006), 12(14), p1864-1865.
• Kim, S.-J., Shin, M.-J., Son, Y.-I., Kim, K.-I., Lim, S.-C., Kang, H.-I., “Design of a Disturbance Observer for DC Motor Speed Control under Load Variation”, (2006), 2006 Conference on Information and Control Systems (CICS 2006), p133-135.
• Choi, Y., Yang, K., Chung, W.K., Kim, H.R., Suh, I.H., “Design of Disturbance Observer Considering Robustness and Control Performance (1) : Analysis on Second Order System”, Journal of Control, Automation and Systems Engineering, (2002), 8(8), p655-664.
• Kim, H.R., Choi, Y., Suh, I.H., Chung, W.K., Park, M.K., Lee, K.H., “Design of Disturbance Observer Considering Robustness and Control Performance (2) : It’s Application for Optical Disc Drive Servo System”, Journal of Control, Automation, and Systems Engineering, (2003), 9(4), p270-276.
• Xiao, H., Wang, S., “Auto-tuning PID module of robot motion system”, (2011, Jun), 2011 6th IEEE Conference on Industrial Electronics and Applications (ICIEA), p668-673. [https://doi.org/10.1109/iciea.2011.5975670]
• Katoh, M., Fujiwara, A., “Auto tuning on robust parameters of a PID controller for a 2nd-order adjusted system with one changeable parameter”, (2007, Sep), SICE Annual Conference 2007, p1624-1630. [https://doi.org/10.1109/sice.2007.4421243]
• Lee, H.S., Robust Digital Tracking Controllers for High-Speed/High-Accuracy Positioning Systems, Ph.D. Dissertation, U.C Berkeley, (1994).
• Ohnishi, K., “A new servo method in mechatronics”, Transactions of Japanese Society of Electric Engineering, (1987), 107-D, p83-86.
• Umeno, T., Hori, Y., “Robust speed control of dc servomotors using two degrees-of-freedom controller design”, IEEE Transactions on Industrial Electronics, (1991), 38(5), p363-368.