생체모방형 수중 다관절 로봇의 추진력 제어를 위한 유영 패턴 재생성

1. 서 론

각종 자원의 고갈로 인해 대체 자원에 대한 관심이 날로 높아지고 있다. 특히, 해양의 경우 지구의 70%를 차지하고 있지만 아직까지 많은 영역이 미지의 영역으로 남아있다. 하 지만 지금까지 발견된 자원과 매장량만으로도 해양에 대한 기대감이 점점 높아지고 있다.

해양은 인간이 직접적으로 탐사하기 어렵다. 그렇기 때문 에 ROV (Remotely Operated Underwater Vehicle)나 AUV (Autonomous Underwater Vehicle)와 같은 수중 로봇을 이 용해 해양을 탐사하고 있다. 위와 같은 수중 로봇은 일반적으 로 프로펠러 형태의 추진기를 사용하여 추진한다. 이러한 프 로펠러 형태의 추진기를 가진 수중 로봇은 강한 조류가 존재 하는 곳에서는 운용하기 어려운 단점이 존재한다. 선박해양 플랜트연구소에서는 위와 같은 문제점을 해결하기 위해서 다관절 다리를 가지고 유영과 보행이 가능한 수중 로봇인 Crabster를 2010년부터 개발하고 있다^1,2]. 일반적인 수중 환경에서는 다관절 다리를 이용하여 유영을 하고 강한 조류 환경이나 정밀 탐색이 필요한 지역에서는 보행을 할 수 있 는 장점이 있다^2,3].

Crabster는 게와 바닷가재의 합성어로 게와 바닷가재의 생체를 모방한 구조를 가지고 있다. 이러한 생체모방을 이 용한 수중 로봇은 주로 물고기를 모방하고 있다^4-6]. 하지만 물고기는 지느러미를 이용하여 유영을 하기 때문에 다관절 다리의 유영에 적용하기 어렵다. 다관절 다리의 유영에 적 용하기 적합한 생명체에는 물방개가 있다. 물방개는 다관 절 다리를 가지고 있으며 효율적으로 유영한다고 알려져 있다^7]. 물방개의 유영을 관찰하여 수중 로봇에 적용한 예로 는 Whirligig-Beetle-Inspired Robot^8]과 CALEB 10^10-12] 이 있다. Whirligig-Beetle-Inspired Robot은 물방개를 관찰 하여 동역학 모델을 만들고 물방개의 생체를 모방한 수중 로봇을 만들었다. 또한, 모델을 이용하여 유영을 에너지 효율 이 높도록 최적화하였다. 하지만, 유영만을 고려했기 때문에 보행에 적합하지 않은 구조를 가지고 있으며 로봇이 물방개 와 다른 형태를 가진 경우에는 적용하기 어렵다. CALEB 10은 물방개가 유영을 할 때 다리 궤적을 관찰하여 유영패턴 생성기인 SPG (Swimming Pattern Generator)를 만들었다. 또한, 발전된 형태의 유영 패턴 생성기인 ESPG (Extended Swimming Pattern Generator)^9,10]를 만들었으며 시뮬레이 션과 실험을 통해 유영 패턴을 검증하였다^10,11]. ESPG는 물 방개의 다리의 움직임만을 모델링하였기 때문에 Whirligig- Beetle-Inspired Robot보다 유영 패턴이 다양하고 다관절 다 리를 가지고 있는 수중 로봇에 적용하기 쉽다. 하지만, ESPG 는 유영 패턴이 결정되면 다음 유영 패턴을 시작할 때까지 추진력을 조절할 수 없는 문제가 있다. 즉, 유영 패턴이 진행 되는 도중에는 추진력을 조절할 수 없다. 따라서 위치나 자세 에 오차가 발생해도 극복할 수 없다.

본 논문에서는 ESPG를 분석하여 유영 패턴이 진행되는 도중에 추진력을 조절할 수 있는 방법을 제안하였다. 제안 된 방법으로 발생하는 문제를 해결하는 방법으로 Phase compensation method와 Synchronization method를 제시 하였다. 제안한 방법을 검증하기 위해서 제어기를 설계하고 시뮬레이션을 진행하였다. 또한, 실제 수중 다관절 로봇인 CALEB 10^10-12]에 제안한 방법과 제어기를 적용하여 검증 하였다.

2. 수중 다관절 유영 로봇(CALBE 10)

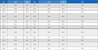
CALEB 10은 물방개의 생체를 모방한 구조로 만들어졌 다. Table 1은 CALEB 10의 제원이다. OS로는 Ubuntu 12.04를 사용하고 있으며 ROS (Robot Operating System) framework를 사용하고 있다. Fig. 1은 CALEB 10의 사진 이다. 4개의 다리가 부착되어 있고 전원공급과 외부와의 통신을 위한 Tether가 있다. CALEB 10의 각 다리는 Fig. 2와 같은 구조로 구성되어 있다^10-12]. 본 논문에서는 type 1인 상태의 다리를 이용하였다.

Table 1

Specification of CALEB 10

Fig. 1

Biomimetic underwater articulated robot: CALEB 10

Fig. 2

Designed CALEB 10 leg

3. 유영 패턴 생성기

3.3 Extended Swimming Pattern Generator의 유영 패턴 분석

3.3.1 Power stroke와 Recovery stroke

ESPG에서 생성된 유영 패턴은 Power stroke 구간과 Recovery stroke 구간으로 나눌 수 있다. Power stroke 구 간은 추진력이 발생하는 구간이며 Recovery stroke는 다음 유영 패턴을 진행하기 위해 이동하는 구간이다. 하나의 유 영 패턴에서는 Power stroke 구간과 Recovery stroke 구간 이 한번씩 나타나며 Power stroke 구간 후에 Recovery stroke 구간이 나타난다.

Fig. 3에서 (a)는 유영 패턴에서 다리 끝의 궤적이고 (b) 는 계산된 추진력이다^13]. (a)에서 실선이 Power stroke 구 간이고 점선이 Recovery stroke 구간이다.

Fig. 3

Relationship between leg trajectory (a) and propulsive force (b)

3.3.2 추진력과 진행속도(k)

추진력은 항력과 관련되어 있다. 일반적으로 항력은 속도 의 제곱에 비례한다. 따라서 유영 패턴의 속도가 변하면 링크의 속도가 변하고 추진력이 변화할 것이라는 것을 짐작 할 수 있다.

식 (1), (2)에서 k를 이용해 각속도를 조절할 수 있다. 또한 유영 패턴의 진행관점에서 본다면 진행속도를 조절하 는 것이라 할 수 있다.

Fig. 4는 ESPG에서 생성된 동일한 유영 패턴에서 진행속 도(k)만 변화시켜가며 계산한 유영 패턴당 추진력이다. 일 정한 구간에서 선형적으로 증가하는 것을 확인할 수 있다.

Fig. 4

Propulsive force vs. k graph

3.4 추진력 조절

3.3.2절의 결과를 통해 진행속도를 조절하면 추진력을 조 절할 수 있다는 것을 확인할 수 있다. 3.4절에서는 유영 패 턴이 진행되는 도중 진행속도를 변경하면 발생하는 문제와 해결방법을 제안하였다.

3.4.1 Phase compensation method

유영 패턴이 진행되는 도중 진행속도를 변경하면 Fig. 5와 같이 각도가 불연속적으로 출력된다. 유영 패턴의 의미 가 사라지며 실제 로봇에서 동작이 불가능한 각도이다. 각 도가 불연속적으로 출력되는 이유는 식 (1), (2)에서 진행속 도만 변화시키고 위상(ψ)을 보상하지 않기 때문이다. 식 (7)을 사용하여 위상을 보상하면 각도가 불연속적으로 출력 되는 문제를 해결할 수 있다.

Fig. 5

Angle vs. time graph

$\[ \Delta \psi =\omega t\left(k_{i-1}-k_i\right) \]$

(7)

$\[ {\theta }_1=U_1{A}_1+U_2{C}_1\text{cos}\left(k_i\omega t+{\psi }_i+\Delta \psi \right) \]$

(8)

$\[ {\theta }_2=M_1{A}_2+M_2{C}_2\text{cos}\left(k_i\omega t+{\psi }_2+\Delta \psi \right) \]$

(9)

k_i-1은 이전의 진행속도, k_i는 변경한 진행속도, t는 현재의 시간이고 ω는 식 (1), (2)의 각속도이다. 식 (1), (2)에 보상 항을 추가하면 식 (8), (9)로 표현된다.

Fig. 6은 Phase compensation method를 적용한 상태에 서 진행속도를 변경한 경우이다. Fig. 5와는 다르게 각도가 연속적으로 출력되는 것을 확인할 수 있다.

Fig. 6

Angle vs. time graph (Applying Phase compensation method)

3.4.2 Synchronization method

진행속도를 변경하면 Fig. 6와 같이 유영 패턴이 종료되 는 시점이 달라진다. 각 다리의 유영 패턴의 종료시점이 다르면 다음 유영 패턴을 결정할 때 많은 요소를 고려해야 한다. 유영 패턴이 종료되는 시점이 동일하면 고려해야하는 요소의 수를 줄일 수 있다.

$\[ k=\frac{\pi +\psi }{\omega \left(T_{end}-t\right)} \]$

(10)

식 (10)을 이용하여 유영 패턴의 종료시점을 정할 수 있 다. ω는 각속도, t는 현재 시간, T_end는 유영 패턴의 종료시 점, ψ는 위상이다. Power stroke에서 Recovery stroke로 넘어가는 순간에 사용할 수 있도록 유도하였다. Fig. 7은 Synchronization method을 사용한 결과이다. 유영 패턴 중 간에 진행속도(k)가 변하였지만 유영 패턴의 종료시점이 동 일한 것을 확인할 수 있다.

Fig. 7

Angle vs. time graph (Applying Synchronization method)

4. 유영 로봇의 오차 극복을 위한 제어기 설계 및 시뮬레이션

3.4절에서 ESPG에서 생성된 유영 패턴에서 진행속도를 변경하여 추진력을 변경하는 방법을 살펴보았다. 4장에서 는 3.4절에서 제안한 방법을 이용하여 제어기를 설계하고 시뮬레이션을 통해 제어가능성을 확인하였다.

4.1 Tracking controller

좌우 추진력이 다르면 회전이 발생한다. 이를 이용해 단 순한 형태의 Tracking controller를 설계하였다. 본 논문의 목적이 유영 패턴이 정해진 상태에서 추진력을 조절하는 것이기 때문에 유영 패턴과 목표 위치는 정해져 있다고 가 정하였다.

Fig. 8은 설계된 제어기의 개념도이다. 현재 위치와 목표 위치를 이용하여 필요한 회전량(θ_d)구하고 θ_d를 이용하여 왼쪽 다리와 오른쪽 다리의 진행속도를 정하게 된다. 식 (11), (12)는 θ_d와 진행속도를 구하는 식이다.

Fig. 8

Concept of the tracking controller

식 (11)은 θ_d를 구하는 과정이다. X_a는 로봇의 위치고 X_g는 Way point의 위치이다. ESPG에서 진행속도의 기본 값은 1이고 좌우의 추진력 차이를 이용하여 회전하기 때문 에 (12)와 같이 표현된다.

$\[ \left[\begin{array}{c}{x}_d\\ y_d\end{array}\right]=\left[\begin{array}{cc}\text{cos}\left({\omega }_a\right)& -\text{sin}\left({\omega }_a\right)\\ \text{sin}\left({\omega }_a\right)& \text{cos}\left({\omega }_a\right)\end{array}\right]\left[\begin{array}{cc}{x}_g& -x_a\\ y_g& -y_a\end{array}\right] \]$

(11)

$\[ \begin{array}{l}r=\sqrt{x_d^2+y_d^2}\\ {\theta }_d=sign\left(y_d\right)a\hspace{0.17em}\text{cos(}\frac{x_d}{r}\text{)}\\ \Delta k\hspace{0.17em}\text{=}\hspace{0.17em}{P}_{gain}{\theta }_d\\ k_L=1-\Delta k\\ k_R=1+\Delta k\end{array} \]$

(12)

식 (12)를 이용하여 진행속도를 조절하면 Fig. 5와 같은 문제가 발생한다. 이를 해결하기위해서 Phase compensation method를 사용하였고 각 유영 패턴의 종료시점을 동기화하 기위해서 Synchronization method를 사용하였다. Synchro nization method은 전체 Recovery stroke 구간의 진행속도 를 결정한다. 따라서 설계된 제어기는 유영 패턴의 Power stroke에서는 식 (11), (12)에 의해서 진행속도가 결정되고 Recovery stroke에서는 식 (10)에 의해서 진행속도가 결정 된다. Fig. 9는 위의 내용을 정리한 제어기의 순서도이다.

Fig. 9

Controller flow diagram

4.3 시뮬레이션

동일한 유영 패턴에서 초기 Heading angle offset을 주고 설계한 제어기를 사용한 경우와 사용하지 않은 경우를 비교 하였다. Heading angle이 차이가 나기 때문에 위치 오차가 발생하게 된다.

Fig. 10은 직진하도록 좌우에 동일한 유영 패턴을 사용하 고 시뮬레이션한 결과이다. (a)는 Heading angle offest를 15°, (b)는 Heading angle offset를 -15°로 입력하였다. 제어 기를 사용한 경우 위치 오차가 줄어든 것을 확인할 수 있다.

Fig. 10

Simulation results (position)

Fig. 11과 Fig. 12는 각각 Heading angle offset이 15°, -15°일 때 Link 1과 Link 2의 각도이다. 진행속도를 조절했 음에도 각도가 연속적인 것을 확인할 수 있다. 또한 주기가 4초로 일정한 것을 확인할 수 있다. 이를 통해 제안한 Phase compensation method, Synchronization method이 정상적 으로 동작하는 것을 확인할 수 있다.

Fig. 11

Simulation results (leg angle, heading angle offset : 15°)

Fig. 12

Simulation results (leg angle, heading angle offset : -15°)

시뮬레이션을 통해 제안한 방법을 사용하면 유영 패턴이 진행되는 도중에도 위치 오차가 줄어드는 것을 확인할 수 있다. 또한, 제안한 방법이 목적대로 유영 패턴의 궤적을 유지하고 유영 패턴의 주기를 일정하게 유지하는 것을 확인 할 수 있다.

5. 실험을 통한 검증 및 결과 분석

5.1 실험 환경 및 조건

Fig. 13은 실제 실험 환경이다. 실험용 수조의 크기는 6.3 × 5.2 × 1.2 m이다. 수조의 중앙에는 위치 추정을 위한 영상처리용 카메라가 달려있다.

Fig. 13

Experiment environment

유영 패턴은 CALEB 10이 직진할 수 있도록 좌우에 같은 유영 패턴을 사용하였다. 또한, 시뮬레이션과는 다르게 유영 패턴의 주기는 5초이다. 시뮬레이션과 동일하게 Heading angle offset이 15°, -15°인 실험을 수행하였다.

5.2 실험 결과 및 결과 분석

Fig. 14는 Heading angle offset이 15°, -15°인 실험 결과 중 하나를 나타낸 것이다. Fig. 14의 결과는 데이터를 분석 하기 어렵기 때문에 Fig. 15, 16의 (a)와 같이 위치 변화량을 표시하였다. 또한 위치 변화량을 이용하여 오차를 구하였다.

Fig. 14

Experiment results (position)

Fig. 15

Experiment results 1 (Heading angle offset : -15°)

Fig. 16

Experiment results 2 (Heading angle offset : 15°)

Fig. 15는 Heading angle offset이 -15°인 경우이다. (a) 는 위치로 목표 위치로 이동하는 것을 확인할 수 있다. (b)는 진행속도이다. 왼쪽 유영 패턴의 진행속도는 증가하고 오른 쪽 유영 패턴의 진행속도는 감속하는 것을 확인할 수 있다. 또한, 2.3 ~ 2.5초 사이에 Synchronization method에 의해 서 진행속도가 변하는 것을 확인할 수 있다. 이 때 부터는 (c), (d)는 각각 Link 1과 Link 2의 각도이다. 각도가 연속적 이고 주기가 5초로 일정한 것을 확인할 수 있다.

Fig. 16은 Heading angle offset이 15°인 경우이다. Heading angle offset이 -15°인 경우실험의 결과와 반대로 오른쪽 유영 패턴의 진행속도는 증가하고 왼쪽 유영 패턴의 진행속 도는 감소하는 것을 확인할 수 있다. 두 실험에서 극복되는 오차가 차이가 나는 것을 확인할 수 있는데 이는 Tether의 장력에 의한 영향이다.

Fig. 17와 Fig. 18은 목표 경로와의 거리 그래프이다. 제 어기가 있는 경우와 없는 경우를 비교하였다. 제어기가 없 는 경우 직진하기 때문에 거리(오차)가 선형적으로 증가하 는 것을 확인할 수 있다.

Fig. 17

The distance between desired path and robot position (Heading angle offset : -15°)

Fig. 18

The distance between desired path and robot position (Heading angle offset : 15°)

실험을 통해 제안한 추진력을 조절하는 방법과 Phase compensation method, Synchronization method을 검증하 였다. 실험에서 제어기에서 고려하지 못한 Tether의 영향에 도 불고하고 위치 오차가 줄어드는 것을 확인할 수 있다.

6. 결 론

선행 연구에서는 ESPG에서 생성된 유영 패턴이 진행중 인 경우에 추진력을 조절할 수 있는 방법이 없었다. 따라서 유영 패턴이 진행하고 있는 중간에 오차가 발생하더라도 유영 패턴이 종료될 때까지 아무런 제어도 할 수 없었다. 이러한 문제점을 해결하기위해서 유영 패턴을 분석하고 유 영 패턴이 진행중에 진행속도(k)를 이용하여 추진력을 조절 할 수 있는 방법을 제안했다. 또한, 진행속도를 변경하면 몇 가지 문제가 발생한다. 이를 해결하기 위해서 본 논문에서는 Phase compensation method와 Synchronization method을 제안하였다.

제안한 방법을 이용하여 실제 제어가 가능한지 확인하기 위해서 단순한 형태의 Tracking controller를 설계하였다. 시뮬레이션을 진행하여 제어가 가능함을 확인하였고 실제 다관절 로봇인 CALEB 10에 적용하여 제안한 방법으로 추진력을 조절할 수 있음을 확인하였다. 실험 결과에서 추 진력을 조절할 수 있는 크기가 작은 것을 확인할 수 있다. 이는 유영 패턴의 궤적을 유지하고 주기를 유지하는 조건을 만족하면서 추진력을 조절하기 때문이다.

본 논문에서는 추진력 조절을 확인하기 위해서 단순한 제어기를 사용하였지만 유영 패턴의 특징과 로봇의 동역학 적 특성을 고려하여 제어기를 설계한다면 더 좋은 결과가 나올 것이라고 생각한다.

Acknowledgments

This work was supported by the Korea Research Institute of Ships & Ocean Engineering for the development of a multi-legged walking & flying subsea robot.

References

• B.-H. Jun, “Multi-legged Seabed Robot Crabster (CR200) for the Exploration of High Tide and Low Visibility Environment,” Journal of Institute of Control, Robotics and Systems, vol.19, no.3, pp.17-28, 2013.
• B.-H. Jun, H. Shim, B. Kim, J.Y. Park, H. Baek, and P.M. Lee, “Preliminary Design of the Multi-Legged Underwater Walking Robot CR200,” Proc. Of the MTS/IEEE Oceans, pp.1-4, 2015.
• B.-H. Jun, H. Shim, J.-Y. Park, B. Kim, and P.-M. Lee, “A New Concept and Technologies of Multi-Legged Underwater Robot for High Tidal Current,” Proc. Of Underwater Technology, 2011, IEEE Symposium on and 2011 Workshop on Scientific Use of Submarine Cables and Related Technologies, 2011.
• D.S. Barrett, M.S. Triantafyllou, and D.K.P. Yue, “Drag Reduction in Fishlike Locomotion,” Journal of Fluid Mechanics, vol.392, pp.183-212, 1999. [https://doi.org/10.1017/S0022112099005455]
• Z. Su, J. Yu, M. Tan, and J. Zhang, “Implementing flexible and fast turning maneuvers of a multijoint robotic fish,” IEEE/ASME Transactions on Mechatronics, vol. 19, no.1, pp.329-338, 2014. [https://doi.org/10.1109/TMECH.2012.2235853]
• A.D. Marchese, C.D. Onal, and D. Rus, “Autonomous Soft Robotic Fish Capable of Escape Maneuvers Using Fluidic Elastomer Actuators,” Soft Robotics, vol.1, no.1, pp.75-87, 2014. [https://doi.org/10.1089/soro.2013.0009]
• W. Nachtigall, “Funktionelle Morphologie, Kinematik und Hydromechanik des Ruderapparates von Gyrinus,” Journal of Comparative Physiology A: Neuroethology, Sensory, Neural, and Behavioral Physiology, vol.45, no.2, pp.193-226, 1961. [https://doi.org/10.1007/BF00297764]
• X. Jia, Z. Chen, A. Riedel, T. Si, W. R. Hamel, and M. Zhang, “Energy-Efficient Surface Propulsion Inspired by Whirligig Beetles,” IEEE Transactions on Robotics, vol. 31, no.6, pp.1432-1443, 2015. [https://doi.org/10.1109/TRO.2015.2493501]
• H.-J. Kim and J. Lee, “Swimming Plans for a Bio-inspired Articulated Underwater Robot,” Institute of Control Robotics and System, vol.19, no.9, pp.782-790, 2013. [https://doi.org/10.5302/J.ICROS.2013.13.9023]
• H.-J. Kim, “Designing a Multi-Legged Underwater Robot by Employing Bio-mimicking Swimming Technique”, Master’s Thesis, Chungnam National University, Daejeon, Republic of Korea, 2015.
• H.-J. Kim, B.-H. Jun, and J. Lee, “Bio-inspired Walking and Swimming Underwater Robot Designing Concept and Simulation by an Approximated Model for the robot,” Journal of Korea Robotics Society, vol.9, no.1, pp.57-66, 2014. [https://doi.org/10.7746/jkros.2014.9.1.057]
• H.-J. Kim, B.-H. Jun, and J. Lee, “Multi-functional Bio-inspired Leg for Underwater Robots,” 2014, IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, 2014.
• B.-H. Jun, “Modeling and Drag-Optimized Joint Motion Planning of Underwater Robotic Arms,” Ph.D. Thesis, Chungnam National University, Daejeon, Republic of Korea, 2006.